Періодичність функцій. Властивості та графіки тригонометричних функцій. Розв’язування вправ

1. Періодичність функцій. Властивості та графіки тригонометричних функцій. Розв’язування вправ.

2. Математичний диктант

.
1.Обчислити: cos210°.
2. Знайти значення виразу
sin 25 cos 5 cos 25 sin 5
3.Спростити вираз
p
p
p
p
cos × cos - sin × sin
7
42
7
42

3.

.4.Обчисліть:
(
o
sin 180 - 30
.
o
) cos ( 360
o
60
5.Спростити вираз
2p
5p
2p
5p
cos
× cos
sin
× sin
7
42
7
42
6. Знайти
p
соs , якщо _ sin = 0,6 і
< <p
2
o
)

4. Періодичність функції

Функція у = f(x) називається
періодичною з періодом Т 0, якщо
для будь-якого х із області
визначення числа х + Т і х – Т також
належать області визначення і
виконується рівність f ( x + Т) = f ( x –
Т) = f( x ).
sin(α + 2πn) = sin α
cos(α + 2πn) = cos α
2 π– періоди функцій синус і косинус

5. Якщо функція у = f(x) періодична і має період Т, то функція у = Af(kx + b), де А, k, b — постійні (k ≠0), також періодична, причому її період дорівнює

Якщо функція у = f(x)
періодична і має період Т, то
функція
у = Af(kx + b), де А, k, b —
постійні (k ≠0), також
періодична,
Т причому її період
дорівнює
k

6. Виконання вправ 1. Обчисліть: a) sin 1470°; б) tg 1860°; в) cos 1140°; r) ctg 1125°.

Виконання вправ
1. Обчисліть: a) sin 1470°;
r) ctg 1125°.
б) tg 1860°;
в) cos 1140°;

7. Графік функції y = sin x

Тригонометричні функції: y = sin x, y = cos x, y = tg x, y=ctg x,
де х – кут в радіанах
Y
y =sin x
1
-2π
-3π
2
-π
-5π -2π -π
6 3 2
-π
3
-π
6
-1
Оπ
6
π
3
π
2
2π 5π
3 6
π
3π
2
Синусоїда
2π
Х

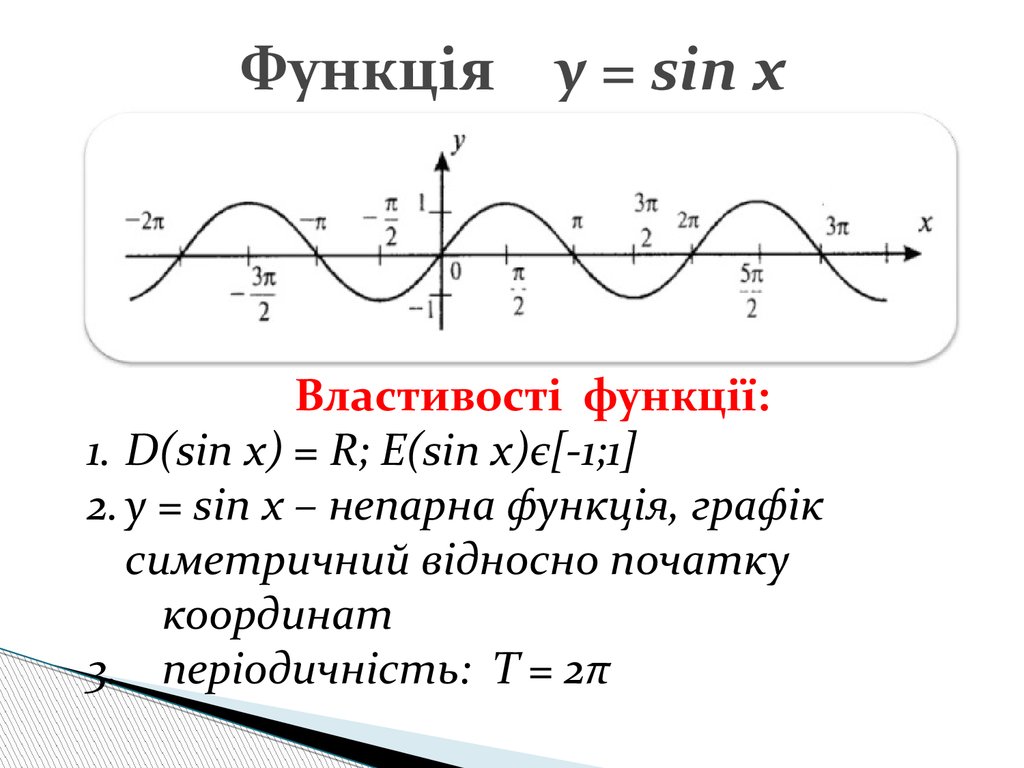
8. Функція y = sin x

Властивості функції:
1. D(sin x) = R; Е(sin x)є[-1;1]
2. y = sin x – непарна функція, графік
симетричний відносно початку
координат
3. періодичність: T = 2π

9.

4. sin x = O при х = πn, n Z (нулі функції)
5. проміжки знакосталості:
sin x > 0 при
0 + 2πn < x < π+ 2πn, n Z
sin x < 0 при
π + 2πn < x < 2π+ 2πn, n Z
6. проміжки монотонності:
x [- π /2 + 2πn; π /2 + 2πn], n Z – зростає
x [ π /2 + 2πn; 3π /2 + 2πn], n Z– спадає
7. екстремуми:
y max = 1 при х = π /2 + 2πn, n Z
y min = - 1 при х = - π /2 + 2πn, n Z
9. похідна:
(sin x )´ = cos x

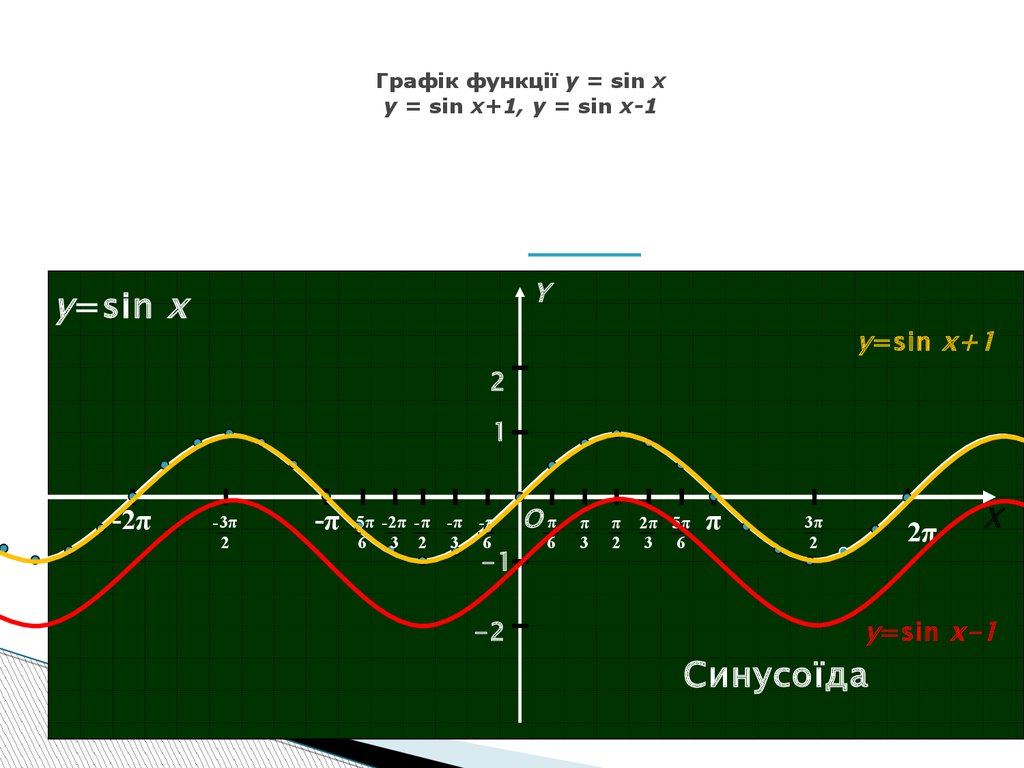
10. Графік функції y = sin x y = sin x+1, y = sin x-1

Y
y =sin x
y =sin x+1
2
1
-2π
-3π
2
-π
-5π -2π -π
6 3 2
-π
3
-π
6
-1
-2
Оπ
6
π
3
π
2
2π 5π
3 6
π
3π
2
2π
Х
y =sin x-1
Синусоїда

11. Графік функції y = sin x y = sin (x- ), y = sin( x+ )

p
p
6
2
Графік функції y = sin x
y = sin (x- ), y = sin( x+ )
Y
y =sin x
p
y =sin
( x)
6
1
-2π
-3π
2
-π
-5π -2π -π
6 3 2
-π
3
-π
6
-1
Оπ
6
π
3
π
2
2π 5π
3 6
π
3π
2
2π
p
y =sin ( x+
Синусоїда
Х
2
)

12. Графік функції y = 2sin x+1, y = sin x, y = 2sin x y = 2sin x+1

Y
y =sin x
y =sin x+1
y =2sin x
2
1
-2π
-3π
2
-π
-5π -2π -π
6 3 2
-π
3
-π
6
-1
Оπ
6
π
3
π
2
2π 5π
3 6
π
3π
2
-2
Синусоїда
2π
Х

13. Графік функції y = cos x

Y
y =sin x
1
-2π
-3π
2
-π
-5π -2π -π
6 3 2
-π
3
-π
6
-1
Оπ
6
π
3
π
2
2π 5π
3 6
π
3π
2
косинусоїда
2π
Х

14.

Функція y = cos x
Властивості функції:
1. D(cos x) = R; Е(sin x)є[-1;1].
2. y = cos x –парна функція,
графік симетричний відносно
осі ординат
3. періодичність: T = 2π

15.

4.
5.
6.
7.
8.
Властивості функції:
cos x = 0 при х = π /2 + πn, n Z (нулі функції)
проміжки знакосталості
cos x > 0 при - π /2 + 2πn < x < π /2 + 2πn, n Z
cos x < 0 при π /2 + 2πn < x < 3π /2 + 2πn, n Z
проміжки монотонності:
x [ π+ 2πn; 2π+ 2πn], n Z –зростає
x [0 + 2πn; π+ 2πn], n Z– спадає
екстремуми:
y max = 1 при х = 2πn, n Z
y min = - 1 при х = π+ 2πn, n Z
похідна:
(cos x )´ = - sin x

16. Графік функції y = 0,5cos x + 2

Y
1
-2π
-3π
2
y =соs x
y = 0.5cos x
y = 0.5cos x + 2
-π
-5π -2π -π
6 3 2
-π
3
-π
6
-1
Оπ
6
π
3
π
2
2π 5π
3 6
π
3π
2
2π
Х

17. Функція y = tg x

Властивості функції:
1. D(ctg x) = x R / πn, n Z
y = ctg x –непарна
функція
графік симетричний
відносно початку
3. періодичніть: T = π
координат
4. tg x = 0 при х = πn, n Z (нулі функції)
5. проміжки знакосталості:
tg x > 0 при 0 + πn < x < π /2 + πn, n Z
tg x < 0 при - π /2 + πn < x < 0 + πn, n Z
2.

18.

6. проміжки монотонності:
x [- π /2 + πn; π /2 + πn], n Z –зростає
7. экстремумів немає
8.E(tg x) = R
9. похідна:
(tg x )´ = 1/cos 2 x

19. Функція y = ctg

Властивості функції:
1.
2.
D(ctg x) = x R / πn, n Z
y = ctg x –непарна функція
графік симетричний
відносно початку
координат
3. періодичність: T = π
4. ctg x = 0 при х = π /2 + πn, n Z (нулі функції)
5. проміжки знакосталості:
ctg x > 0 при 0 + πn < x < π /2 + πn, n Z
ctg x < 0 при π /2 + πn < x < π + πn, n Z

20.

6. проміжки монотонності:
x [0+ πn; π+ πn], n Z – спадає
7. екстремумів немає
8.E(ctg x) = R
9. похідна:
(ctg x )´ = - 1/sin 2 x