Похожие презентации:
Производная. Её геометрический и физический смысл
1.
Производная.Её геометрический
и физический
смысл.
Автор: Брызгалова Наталья Юрьевна
Преподаватель Архангельского
техникума строительства и экономики
2.
Содержание1. Понятие производной.
2. Алгоритм нахождения производной.
3. Примеры.
4. Геометрический смысл производной
5. Физический смысл производной.
6. Таблица производных.
7. Правила нахождения производных.
8. Производная сложной функции
3. Понятие производной
∆fy′= f ′(x) = lim
∆x→0 ∆x
у
∆f – приращение функции
∆x – приращение аргумента
f(x0)
у = f(x)
∆f
f(x0 + ∆х)
∆х
0
х0
х0+ ∆х
х
4. Определение производной
Производной функции у = f(x), заданной нанекотором интервале (a; b), в некоторой точке х
этого интервала называют предел отношения
приращения
функции
в
этой
точке
к
соответствующему приращению аргумента, когда
приращение аргумента стремится к нулю.
у=f ′(x) = lim
∆x→0
∆f
∆x
Нахождение производной называют
дифференцированием
5.
Алгоритм нахожденияпроизводной
1. Зафиксировать значение х0 , найти f(x0).
2. Дать аргументу х0 приращение ∆х, перейти в новую
точку х0 + ∆х, найти f(x0 + ∆х).
3. Найти приращение функции: ∆f = f(x0 + ∆х) – f(x0).
4. Составить отношение
5. Вычислить
∆f
.
∆х
lim ∆f .
∆x→0
∆х
6. Этот предел и есть у′=f ′(x0).
Если функция имеет производную (дифференцируема) в
точке х, то она непрерывна в этой точке.
6. Пример №1
1. Найти производную функции y = kx + b в точке хoРешение
1. f x o kxo b
2. f x o Δx k x o Δx b
3. Δf f x o Δx f x o k x o Δx b kxo b
kxo k Δx b kxo b k Δx
Δf
k Δx
4.
k
Δx
Δx
Δf
5. lim
lim k k
Δx 0 Δ x
Δx 0
kx b k
7. Пример №2
2. Найти производную функции y = C (C – const) в точке хoРешение
1. f xo С
2. f x o Δx С
3. Δf f x o Δx f x o С С 0
Δf
0
4.
0
Δx Δx
Δf
5. lim
lim 0 0
Δx 0 Δ x
Δx 0
С 0
8. Пример №3
3. Найти производную функции y = x2 в точке хo1. f xo xо
Решение
2
2. f xo Δx xo Δx
2
3. Δf f x o Δx f x o x o Δx x o
2
2
x о2 2 x o Δx Δx 2 x о2 2 x o Δx Δx 2
2x o Δx Δx 2 Δx 2 x o Δx
Δf
4.
2 x o Δx
Δx
Δx
Δx
Δf
5. lim
lim 2 x o Δx 2 x o
Δx 0 Δ x
Δx 0
x 2х
2
9. Пример №4
4. Найти производную функции уx в точке хo
Решение
1. f x o x o
2. f x o Δx x o Δx
3. Δf f x o Δx f x o x o Δx x o
x Δx x x Δx x x Δx x
2
o
o
o
o
o
x o Δx x o
x o Δx x o
Δx
x o Δx x o
x o Δx x o
Δf
4.
Δx Δx
Δx
x o Δx x o
2
o
x o Δx x o
1
x o Δx x o
10.
Δf4.
Δx Δx
Δx
x o Δx x o
1
x o Δx x o
Δf
1
1
5. lim
lim
2 x
Δx 0 Δx
Δx 0 x Δx
x
o
o
o
x
1
2 х
11. Примеры №5
5. Найти производную функции y = 1/x в точке хoРешение
1
1. f x o
xо
1
2. f x o Δx
x o Δx
1
1
3. Δf f x o Δx f x o
x o Δx x o
x o x o Δx
Δx
2
x o x o Δx
x о x o Δx
Δf
Δx
1
4.
2
2
Δx Δx x о x o Δx
x о x o Δx
12.
ΔfΔx
1
4.
2
2
Δx Δx x о x o Δx
x о x o Δx
Δf
1
1
2
5. lim
lim 2
Δx 0 Δx
Δx 0 x x Δx
xо
o
о
1
1
2
х
х
13.
Геометрический смыслпроизводной
y f ( x0 ) kкас tg
У
y=f(x)
k – угловой коэффициент
касательной
y=kx+b
f(x0)
х0
Х
Производная данной
функции y=f(x) в данной
точке х0 равна угловому
коэффициенту касательной,
проведённой к графику
функции в этой точке.
14.
Физический смыслпроизводной
Производная функции y=f(x) в точке х0 – это
скорость изменения функции f(x) в точке х0.
Производная выражает мгновенную скорость в
момент времени t.
Если при прямолинейном движении путь S, пройденный
точкой, есть функция от времени t, т.е. S = S(t), то
мгновенная скорость точки есть производная от пути
по времени, т.е.
v(t) = S′(t)
S = S(t)
0
М
Х
15. Понятие производной широко используется в современной физике. Приведём несколько примеров.
Скорость: V(t)=S′ (t) – перваяпроизводная от перемещения по времени;
Ускорение: a(t)=V′(t) – первая производная
от скорости по времени;
Сила тока – I(t)=q′(t) – первая производная
от заряда по времени;
Мощность: N(t)=A′(t) – первая
производная от работы по времени.
16. Таблица производных
(С ) 0( x) 1
1
1
2
x
x
( x n ) n x n 1
( x )
(a ) a ln a
x
(e ) e
x
x
x
1
(log a x)
x ln a
1
(ln x)
x
1
2 x
(sin x) cos x
(cos x) sin x
1
(tgx)
2
cos x
1
(ctgx) 2
sin x
17. Правила нахождения производной
1. Если функции u(x) и v(x) имеют в точке хпроизводные, то их сумма u(x) + v(x) также имеет
в этой точке производную, причем
(u + v)′ = u′ + v′
2. Если функция u(x) имеет в точке х производную и
С – данное число, то функция С∙u(x) также имеет в
этой точке производную, причем
(Сu)′ = С∙u′
18.
3. Если функции u(x) и v(x) имеют в точке хпроизводные, то их произведение u(x) ∙ v(x)
также имеет в этой точке производную, причем
(u ∙ v)′ = u′∙v + u∙v′
4. Если функции u(x) и v(x) имеют в точке х
производные и v(x) ≠ 0, то функция
u(x)
v(x) также
имеет в этой точке производную, причем
u u v uv
2
v
v
19. Производная сложной функции
(f(g(x)))′ = f′(g(x))∙g′(x)Примеры:
1. ((5x – 3)3)′ = 3(5x – 3)2∙(5x – 3)′ =
= 3(5x – 3)2 ∙ 5 = 15(5x – 3)2
2. (sin(4x + 8))′ = cos(4x + 8)∙(4x + 8)′ =
= cos(4x + 8)∙4 = 4 cos(4x + 8)









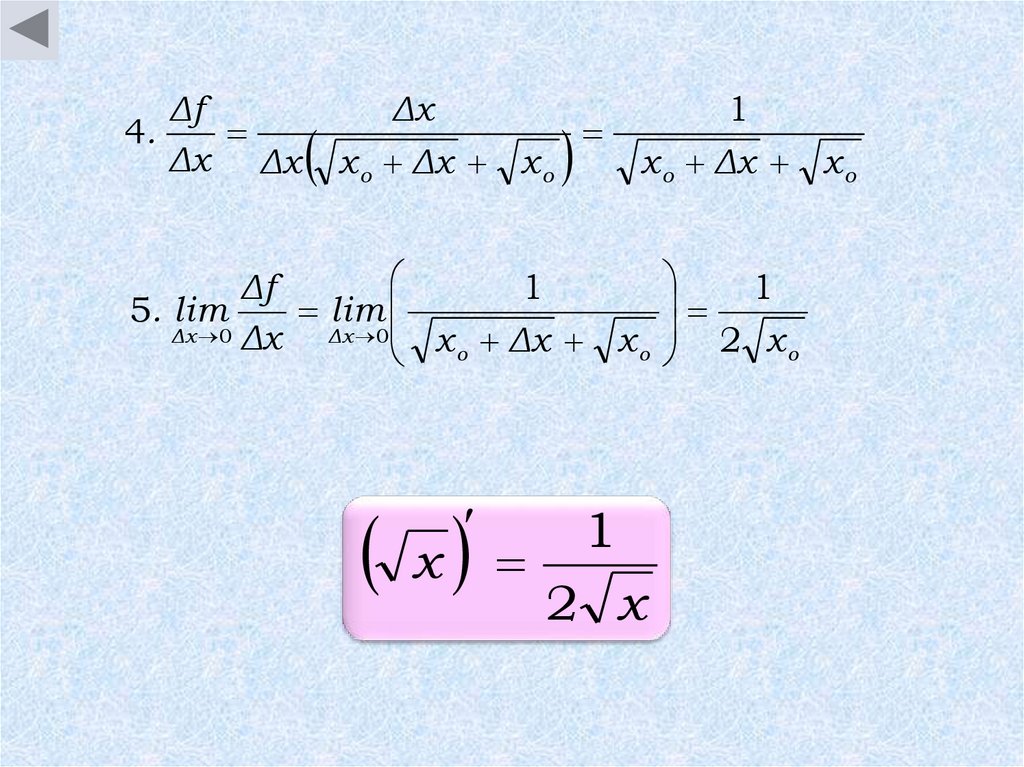









 Математика
Математика








