Сечение многогранников плоскостью

1.

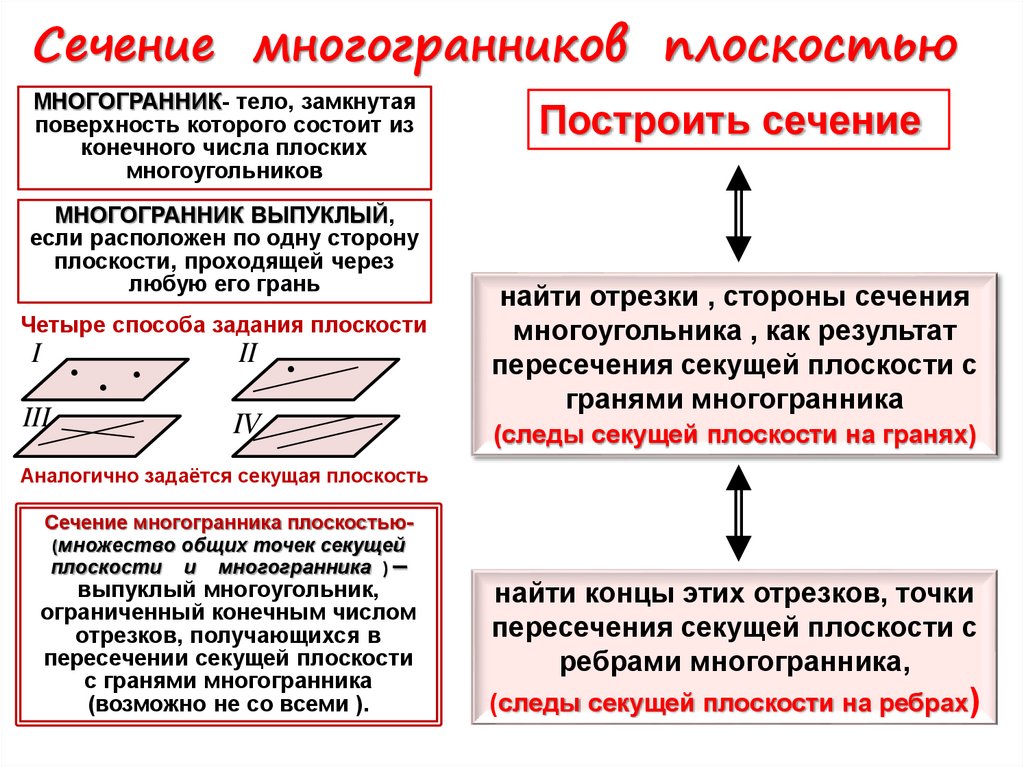
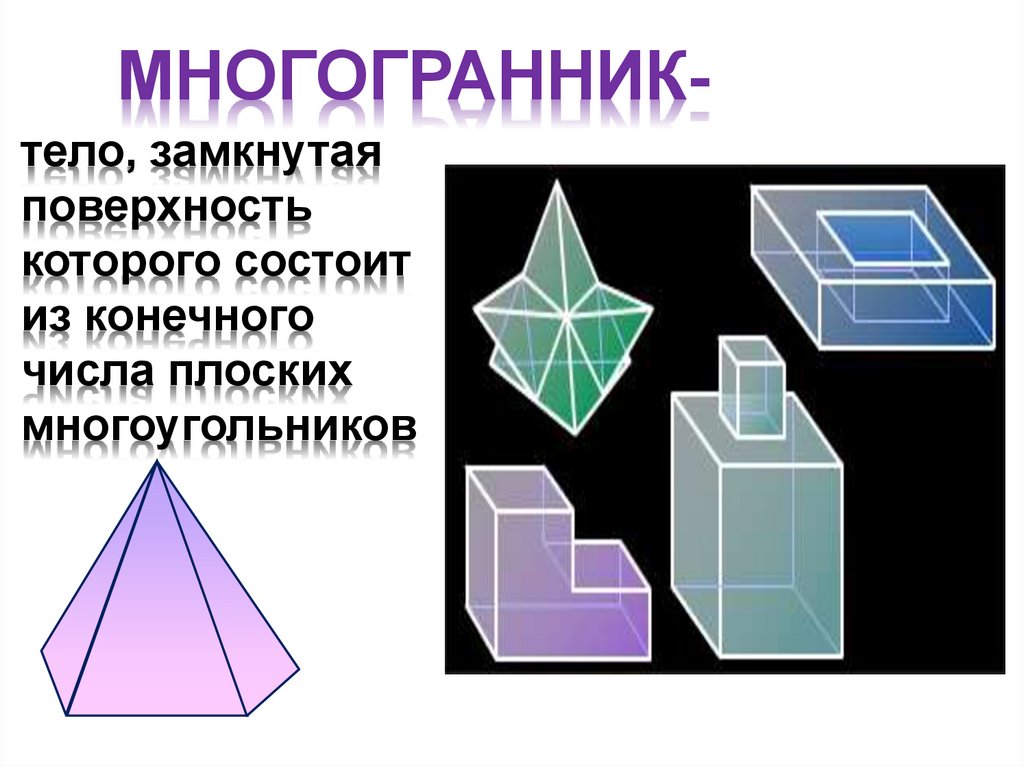
Сечение многогранников плоскостью
МНОГОГРАННИК- тело, замкнутая
поверхность которого состоит из
конечного числа плоских
многоугольников
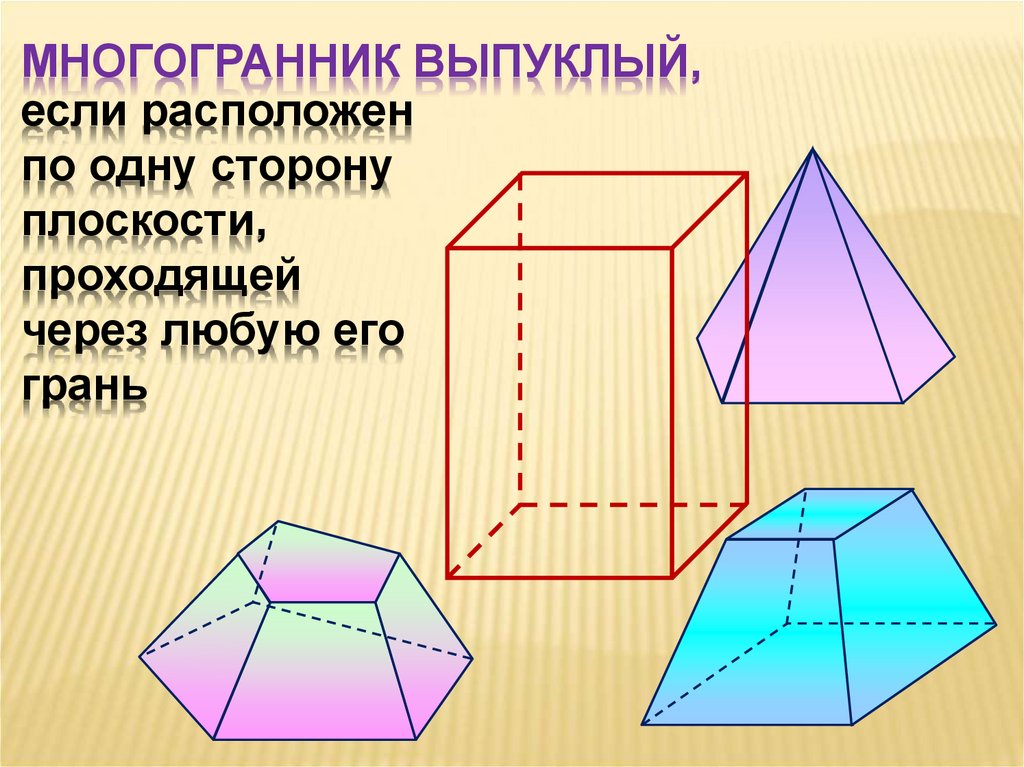
МНОГОГРАННИК ВЫПУКЛЫЙ,
если расположен по одну сторону
плоскости, проходящей через
любую его грань
Четыре способа задания плоскости
I
III
II
IV
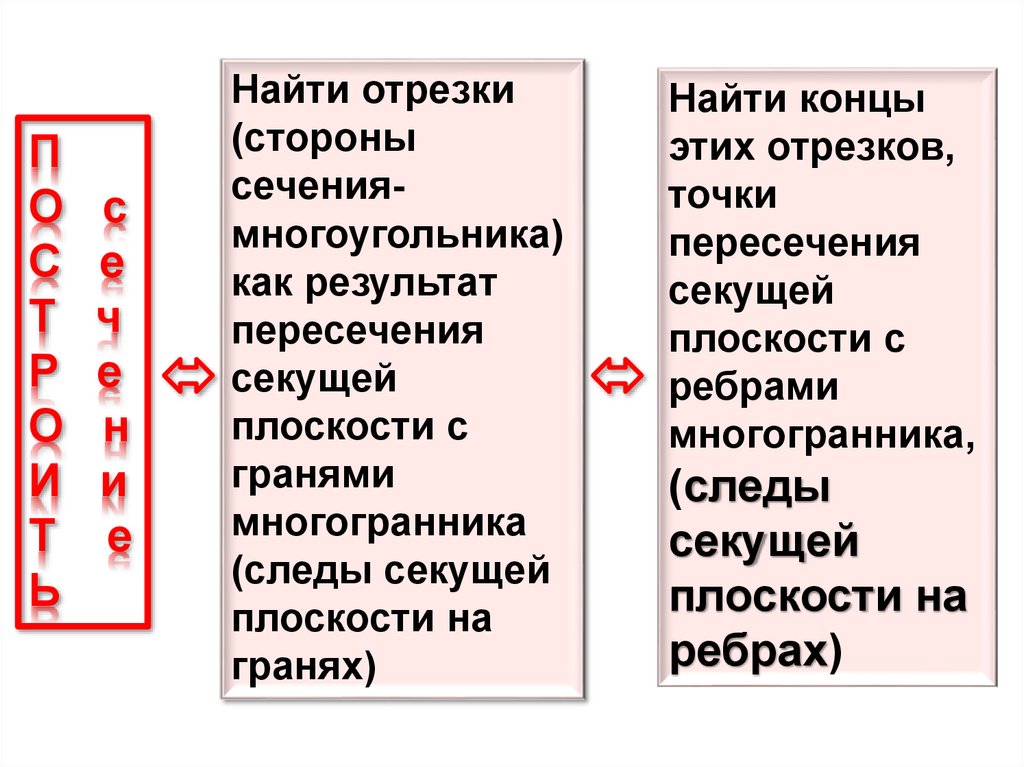
Построить сечение
найти отрезки , стороны сечения
многоугольника , как результат
пересечения секущей плоскости с
гранями многогранника
(следы секущей плоскости на гранях)
Аналогично задаётся секущая плоскость
Сечение многогранника плоскостью(множество общих точек секущей
плоскости и многогранника ) –
выпуклый многоугольник,
ограниченный конечным числом
отрезков, получающихся в
пересечении секущей плоскости
с гранями многогранника
(возможно не со всеми ).
найти концы этих отрезков, точки
пересечения секущей плоскости с
ребрами многогранника,
(следы секущей плоскости на ребрах)

2.

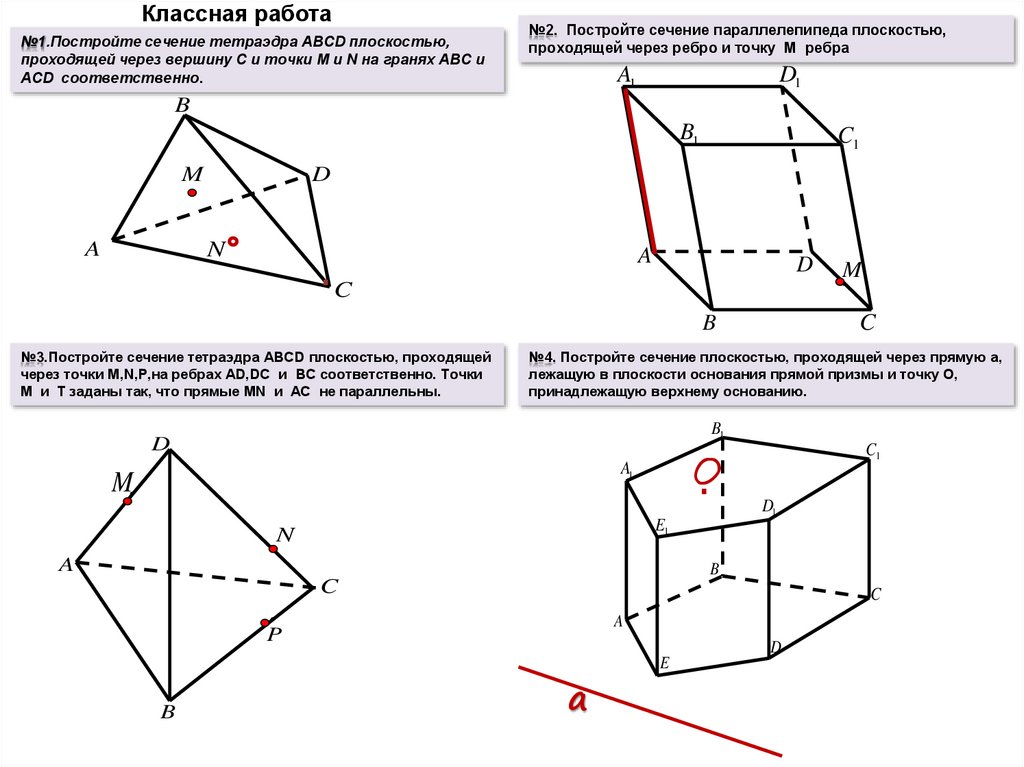
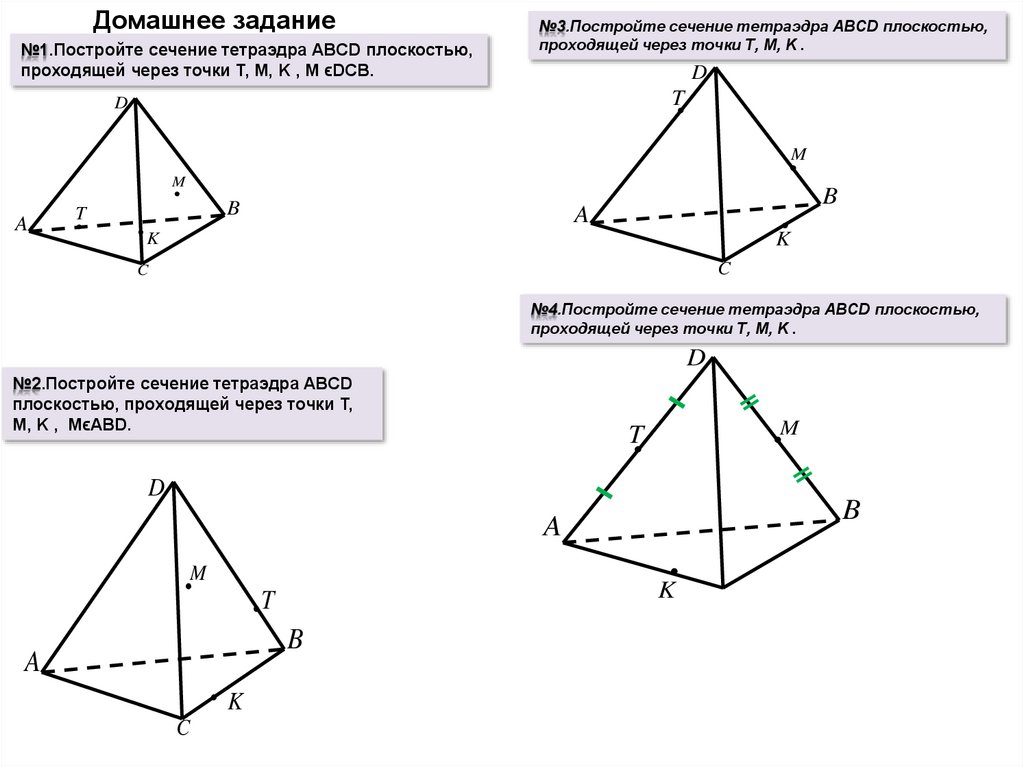
Классная работа
№1.Постройте сечение тетраэдра ABCD плоскостью,
проходящей через вершину С и точки M и N на гранях ABC и
ACD соответственно.
№2. Постройте сечение параллелепипеда плоскостью,
проходящей через ребро и точку M ребра
A1
D1
B
B1
M
A
C1
D
N
A
D
·C
C
B
№3.Постройте сечение тетраэдра ABCD плоскостью, проходящей
через точки M,N,P,на ребрах AD,DC и BC соответственно. Точки
M и Т заданы так, что прямые MN и AC не параллельны.
M
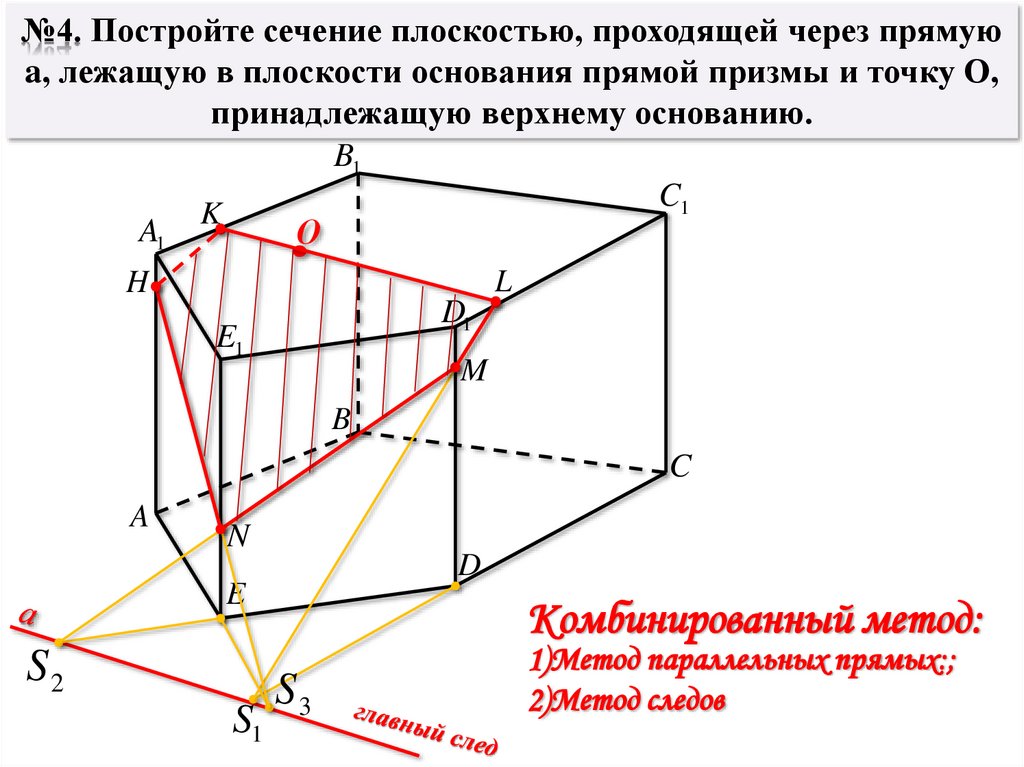
№4. Постройте сечение плоскостью, проходящей через прямую a,
лежащую в плоскости основания прямой призмы и точку О,
принадлежащую верхнему основанию.
B1
D
О
A1
M
E1
N
A
·
C1
D1
B
C
C
A
P
B
D
а
E

3.

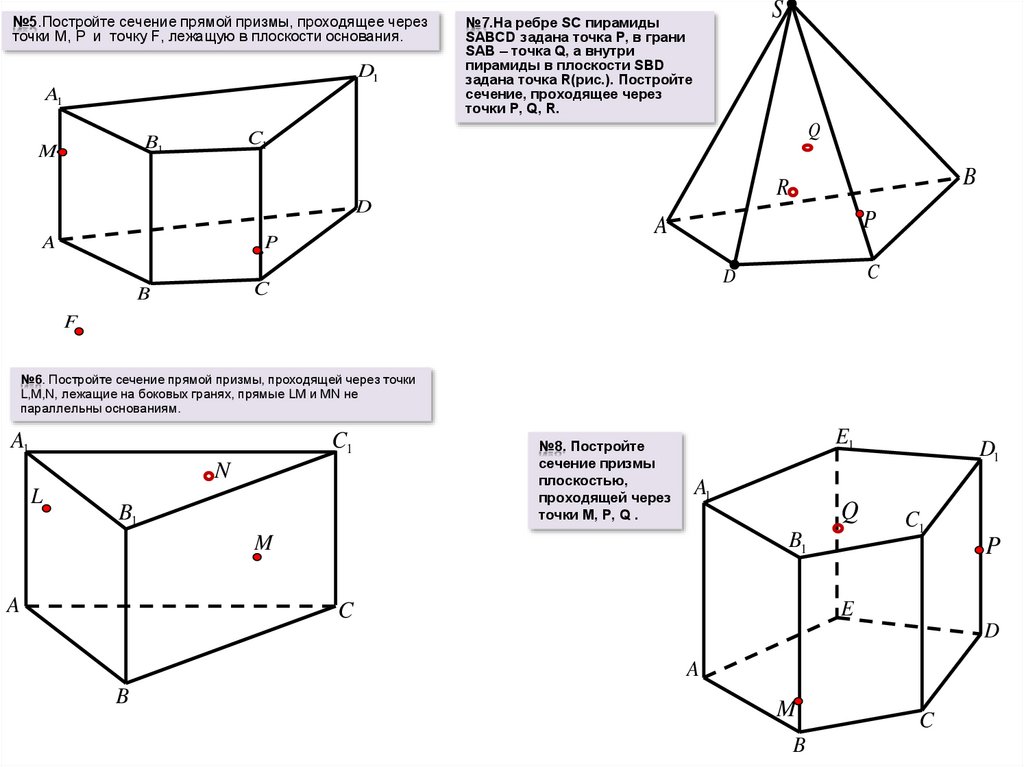
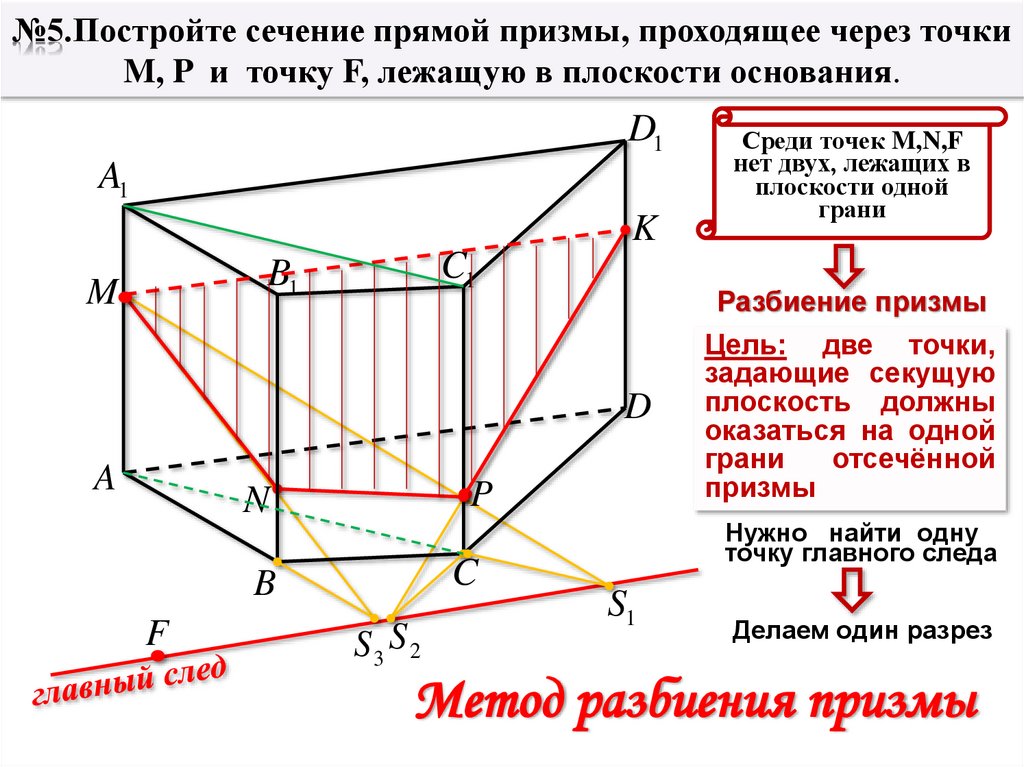
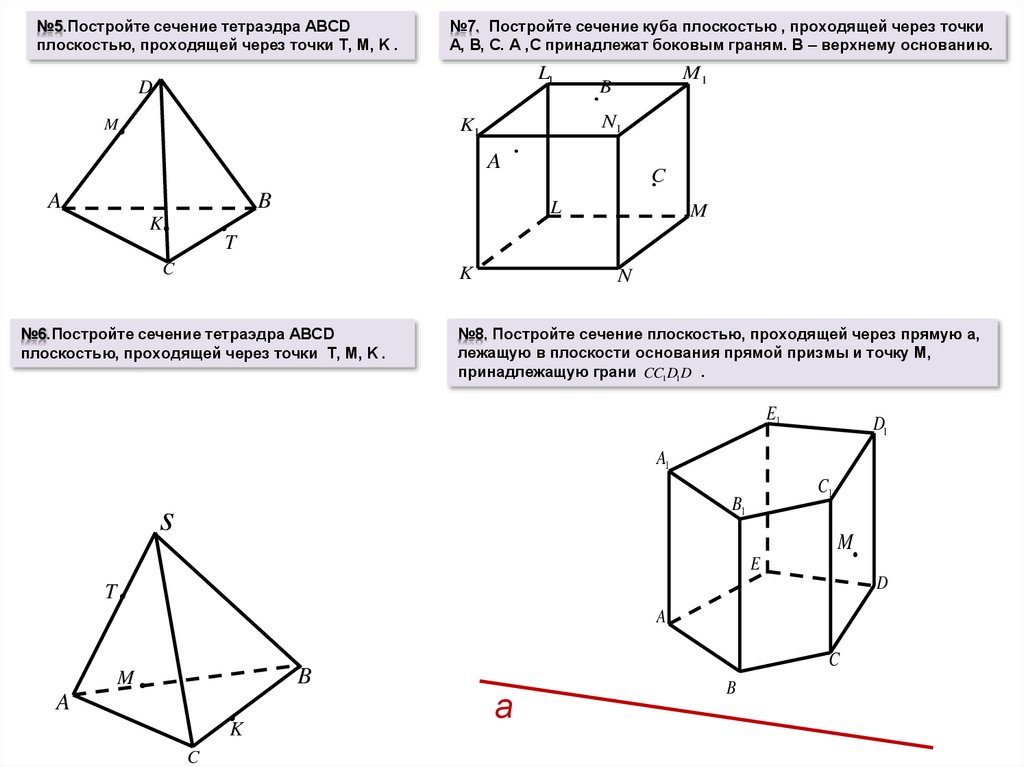
№5.Постройте сечение прямой призмы, проходящее через
точки M, P и точку F, лежащую в плоскости основания.
D1
A1
Q
C1
B1
M
S
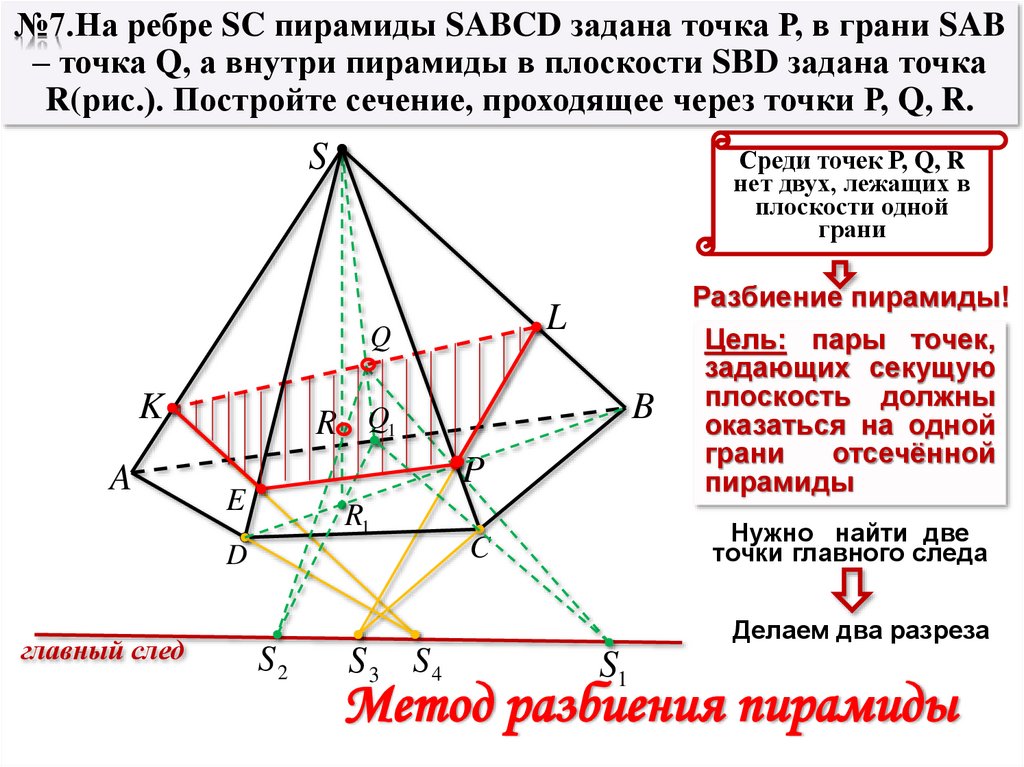
№7.На ребре SC пирамиды
SABCD задана точка Р, в грани
SAB – точка Q, а внутри
пирамиды в плоскости SBD
задана точка R(рис.). Постройте
сечение, проходящее через
точки Р, Q, R.
D
A
P
P
A
C
D
C
B
B
R
F
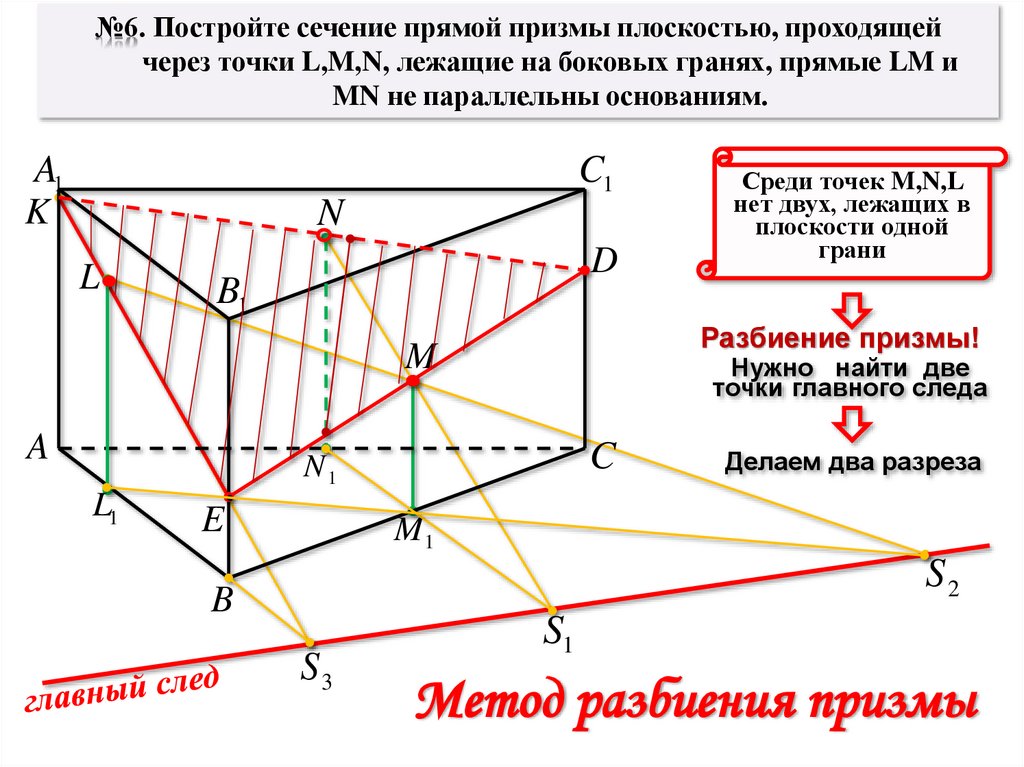
№6. Постройте сечение прямой призмы, проходящей через точки
L,M,N, лежащие на боковых гранях, прямые LM и MN не
параллельны основаниям.
A1
C1
N
L
B1
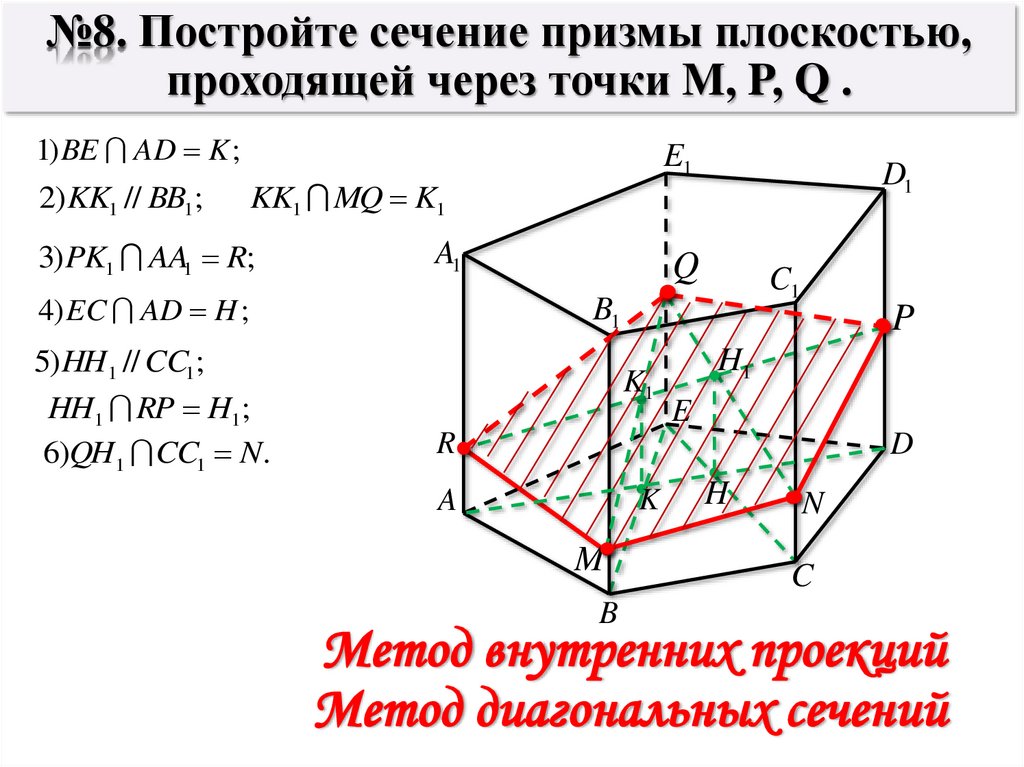
№8. Постройте
сечение призмы
плоскостью,
проходящей через
точки M, P, Q .
E1
A1
B1
M
A
Q
D1
C1
P
E
C
D
A
B
M
B
C

4.

СЕЧЕНИЯ
МНОГОГРАННИКОВ

5.

Построение сечений относится к конструктивным
задачам геометрии, обширной и глубоко развитой
области математики. Конструктивная геометрия тесно
связана с различными сферами математики, а также
практической деятельностью человека:
- техническое конструирование;
- архитектура;
- строительство;
- скульптура;
- изобразительное искусство и т . Д .
Например, построение перспективы в
изобразительном искусстве-вполне научная
тема для исследования с точки зрения законов
геометрии конструктивных особенностей
пространства и способов его изображения.

6.

КОНСТРУКТИВНАЯ
ГЕОМЕТРИЯ
В ПРОИЗВЕДЕНИЯХ
САЛЬВАДОРА
ДАЛИ

7.

Аппарат и рука 1927 г.

8.

Явление лица Афродиты Книдской в пейзаже, 1981 г.

9.

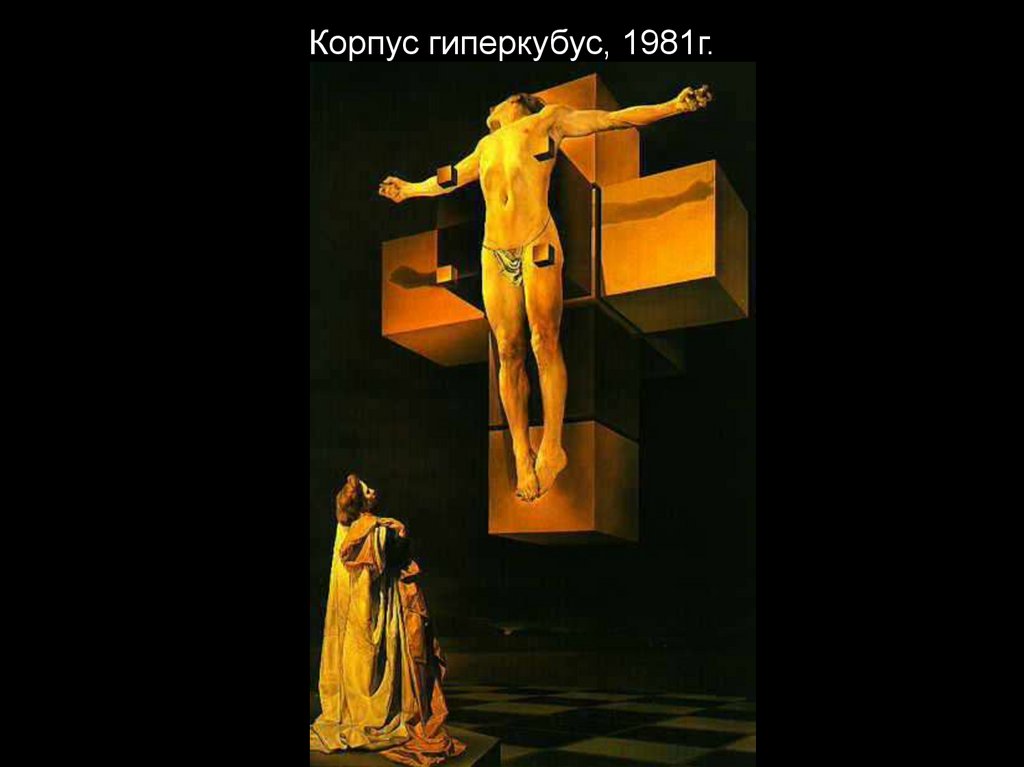
Корпус гиперкубус, 1981г.

10.

Этюды к картине «Атомная Леда», 1947 г.

11.

Атомная Леда, 1949 г.

12.

Мы абстрагируемся от физических и
эстетических свойств пространства и тел.
Нас интересуют конструктивные особенности
взаимодействия стереометрических тел , а
именно многогранников, и пересекающих их
плоскостей . Изучать сечения многогранников
плоскостью мы будем не по наитию,а на основе
законов геометрии.
Ставятся две задачи:
1.Повторить законы стереометрии.
2.Изучить различные методы построения
сечений многогранников плоскостью на основе
законов стереометрии, применить их на
практике.

13.

МНОГОГРАННИКтело, замкнутая
поверхность
которого состоит
из конечного
числа плоских
многоугольников

14.

МНОГОГРАННИК ВЫПУКЛЫЙ,
если расположен
по одну сторону
плоскости,
проходящей
через любую его
грань

15.

Сечение многогранника(множество общих точек секущей
плоскости и многогранника ) –
выпуклый многоугольник,
ограниченный конечным числом
отрезков, получающихся в пересечении
секущей плоскости с гранями
многогранника (возможно не со всеми ).

16.

П
О с
С е
Т ч
Р е
О н
И и
Т е
Ь
Найти отрезки
(стороны
сечениямногоугольника)
как результат
пересечения
секущей
плоскости с
гранями
многогранника
(следы секущей
плоскости на
гранях)
Найти концы
этих отрезков,
точки
пересечения
секущей
плоскости с
ребрами
многогранника,
(следы
секущей
плоскости на
ребрах)

17.

Четыре способа задания плоскости
I
II
III
VI
Аналогично задается
секущая плоскость

18.

Блиц-опрос
D1
С1
K
А1
B1
D
А
H
С
В
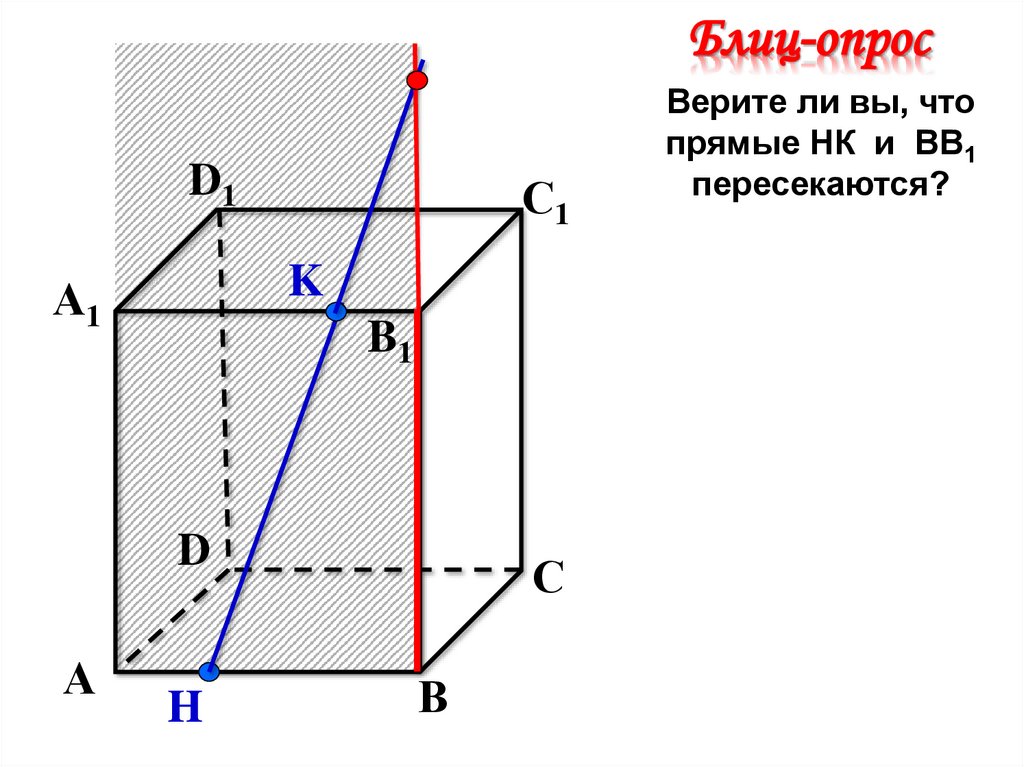
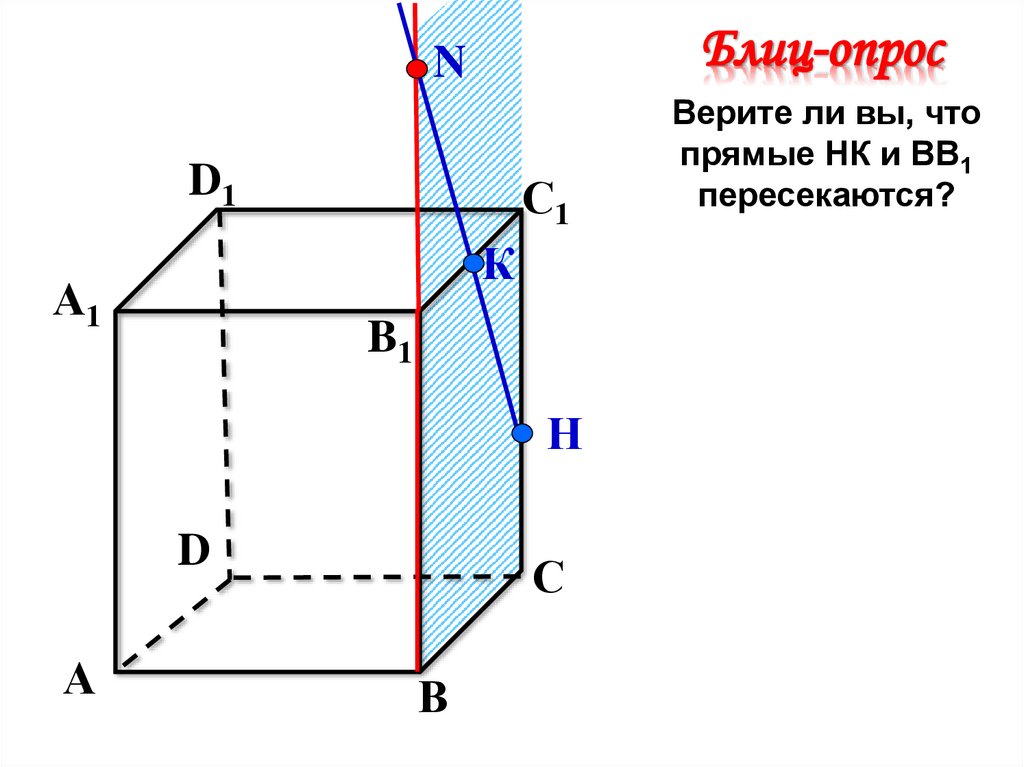
Верите ли вы, что
прямые НК и ВВ1
пересекаются?

19.

Блиц-опрос
N
D1
С1
К
А1
B1
Н
D
А
С
В
Верите ли вы, что
прямые НК и ВВ1
пересекаются?

20.

Блиц-опрос
D1
А1
С1
М
B1
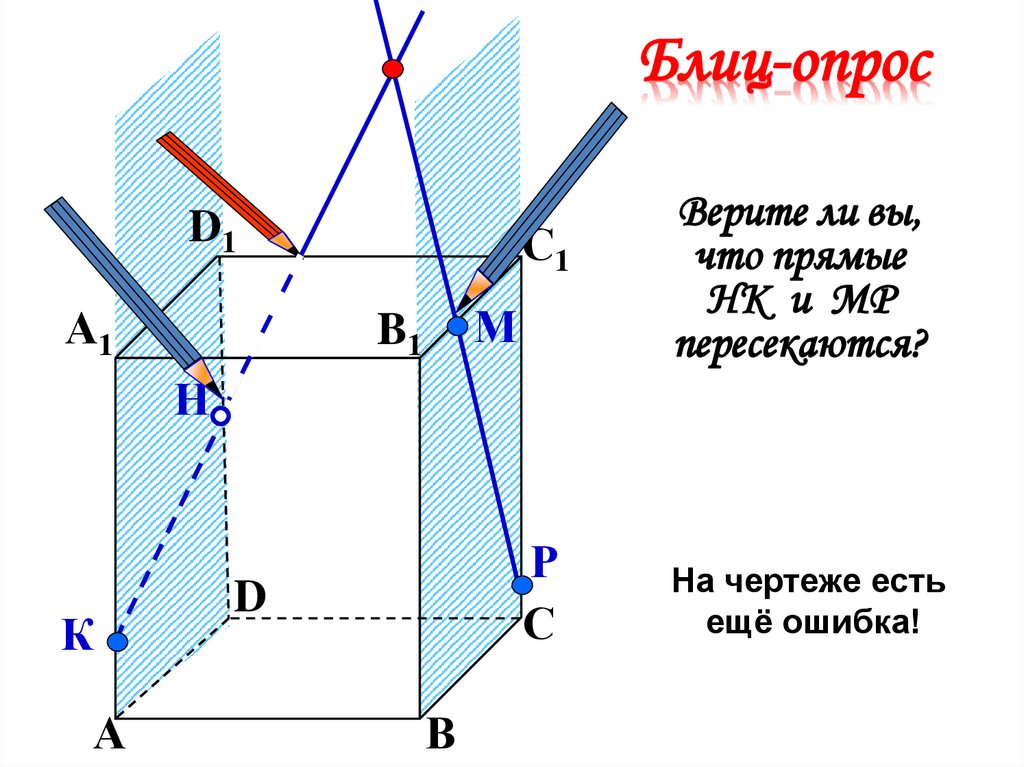
Верите ли вы,
что прямые
HK и MP
пересекаютcя?
Н
К
А
Р
С
D
В
На чертеже есть
ещё ошибка!

21.

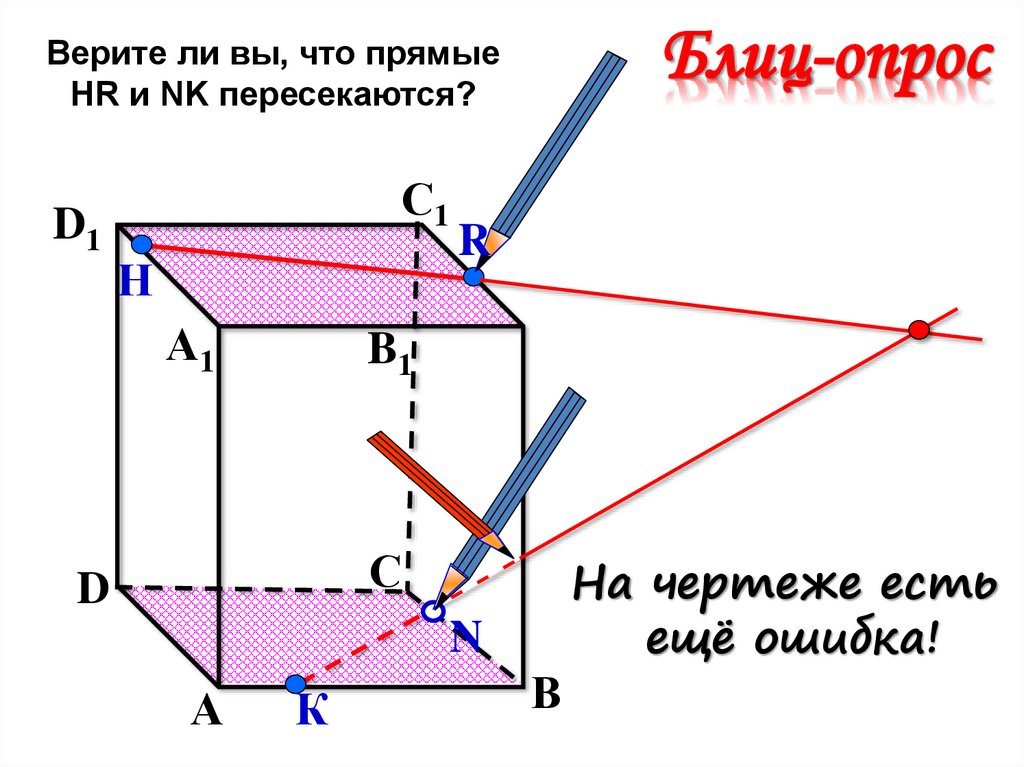
Блиц-опрос
Верите ли вы, что прямые
НR и NK пересекаются?
D1
С1
Н
А1
R
B1
На чертеже есть
ещё ошибка!
С
D
N
А
К
В

22.

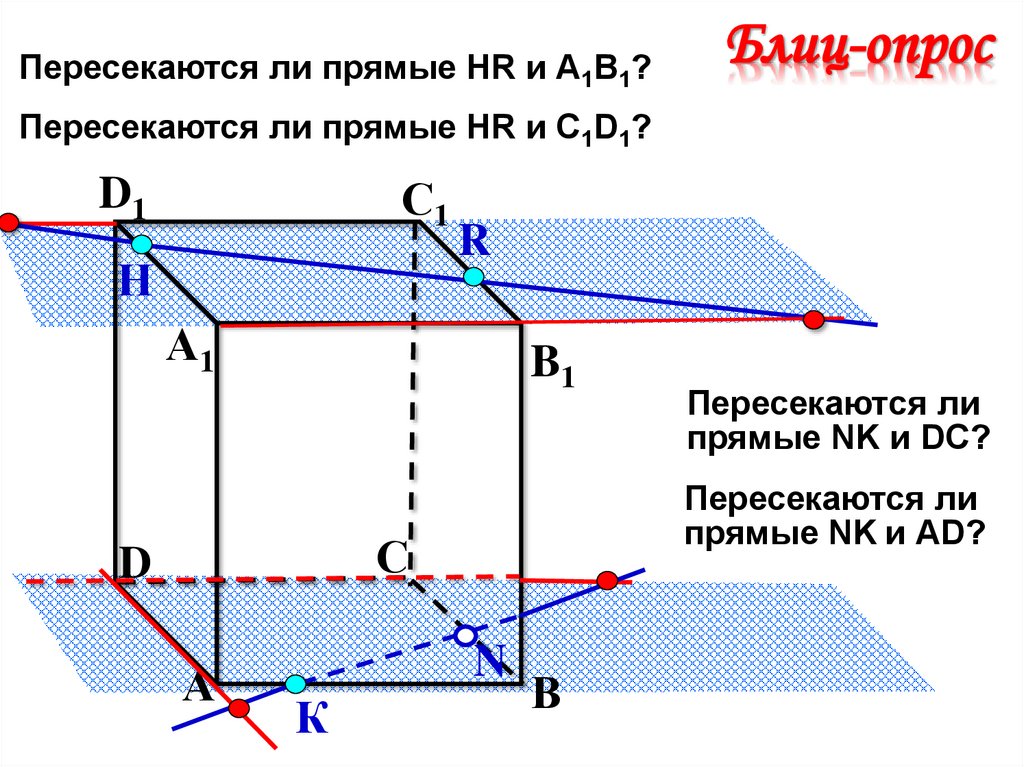
Пересекаются ли прямые НR и А1В1?
Блиц-опрос
Пересекаются ли прямые НR и С1D1?
С1
D1
Н
R
А1
B1
Пересекаются ли
прямые NK и АD?
С
D
А
N
К
Пересекаются ли
прямые NK и DC?
В

23.

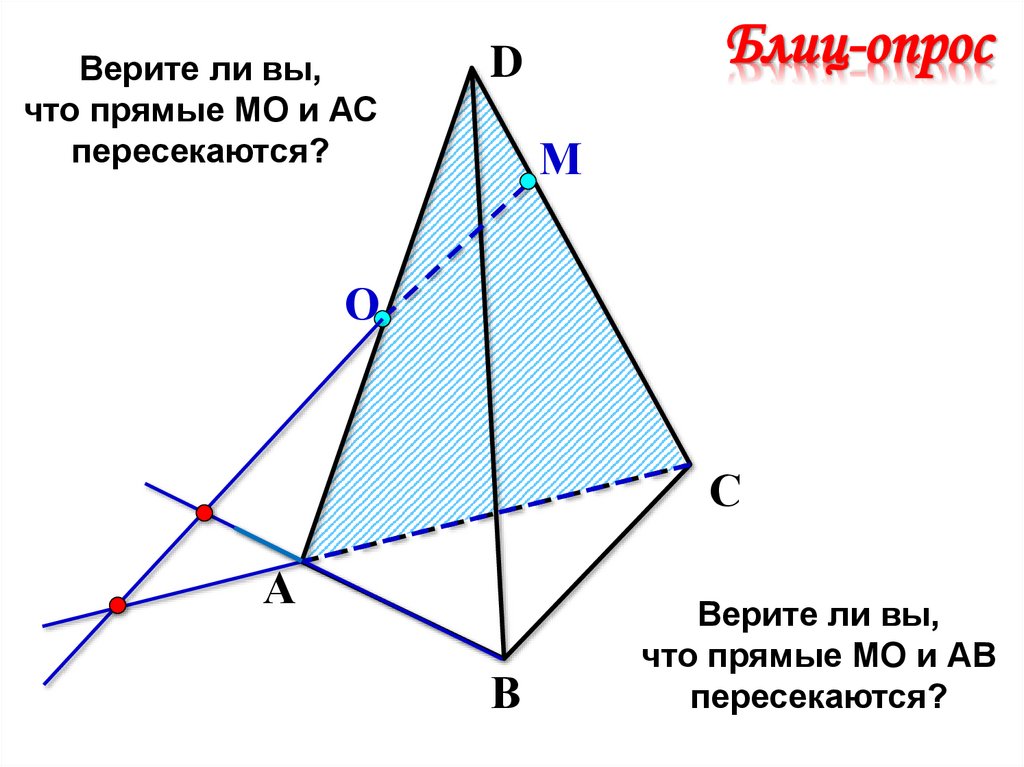
Верите ли вы,
что прямые МО и АС
пересекаются?
Блиц-опрос
D
М
О
С
А
В
Верите ли вы,
что прямые МО и АВ
пересекаются?

24.

Каждый изучающий стереометрию
должен “видеть”
динамику (последовательность)
и диалектику построения
изображения геометрической
фигуры на рисунке (чертеже). Мы
“сняли фильм” о построении
сечения куба…
Е.В. Потоскуев, Л.И.Звавич

25.

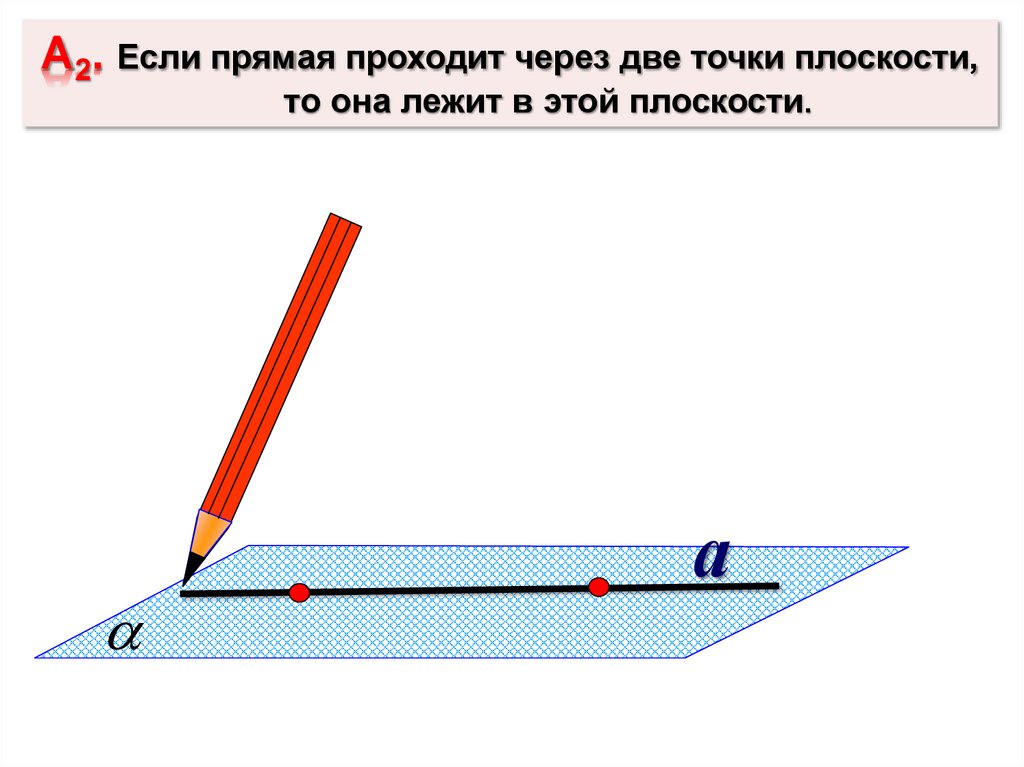
А2. Если прямая проходит через две точки плоскости,
то она лежит в этой плоскости.
а

26.

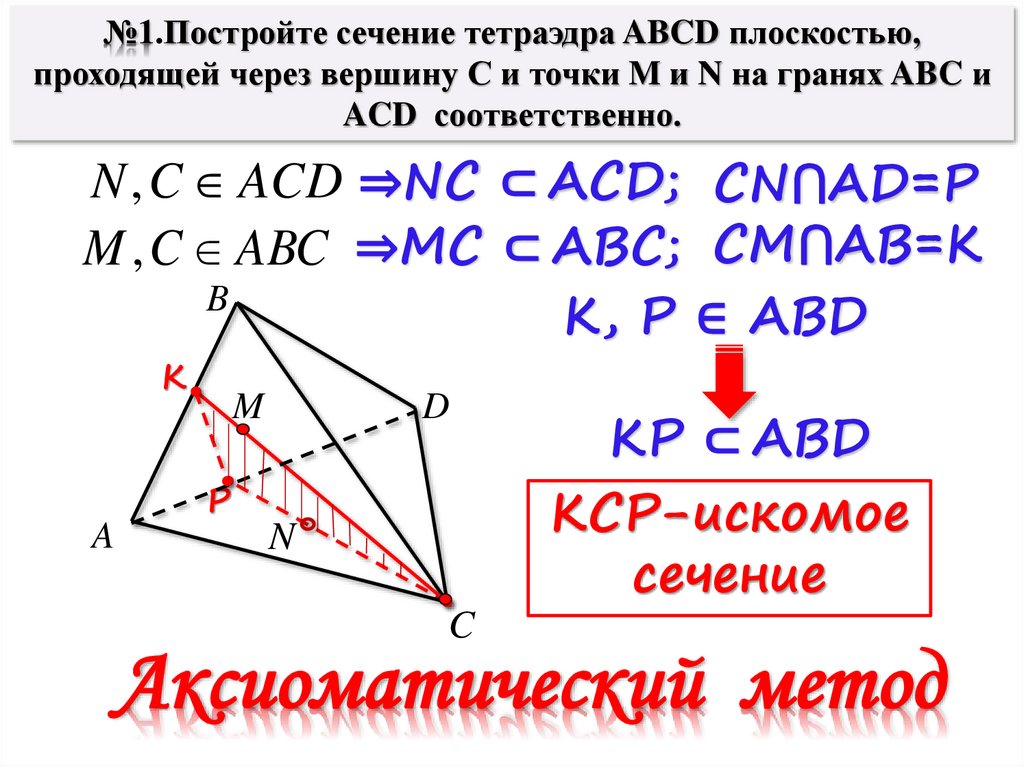
№1.Постройте сечение тетраэдра ABCD плоскостью,
проходящей через вершину С и точки M и N на гранях ABC и
ACD соответственно.
N , C ACD ⇒NC ⊂ ACD; CN⋂AD=P
M , C ABC ⇒MC ⊂ ABC; CM⋂AB=K
B
K, P ∈ ABD
K
A
M
P
D
N
·C
KP ⊂ ABD
KCP-искомое
сечение
Аксиоматический метод

27.

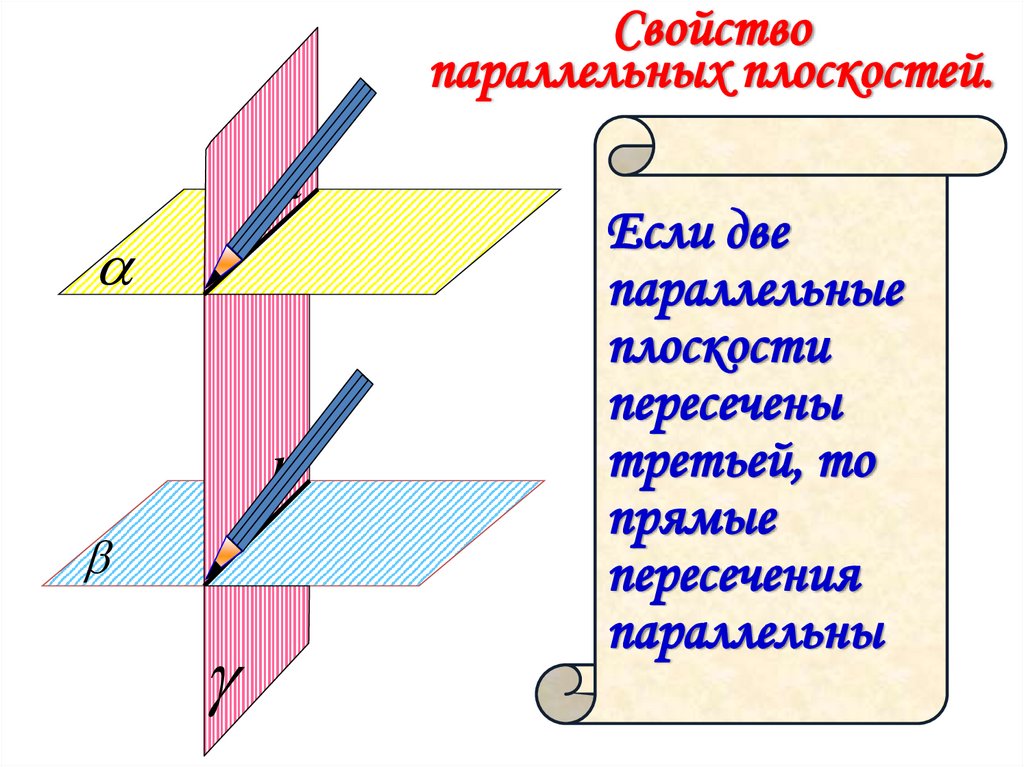
Свойство
параллельных плоскостей.
а
b
Если две
параллельные
плоскости
пересечены
третьей, то
прямые
пересечения
параллельны

28.

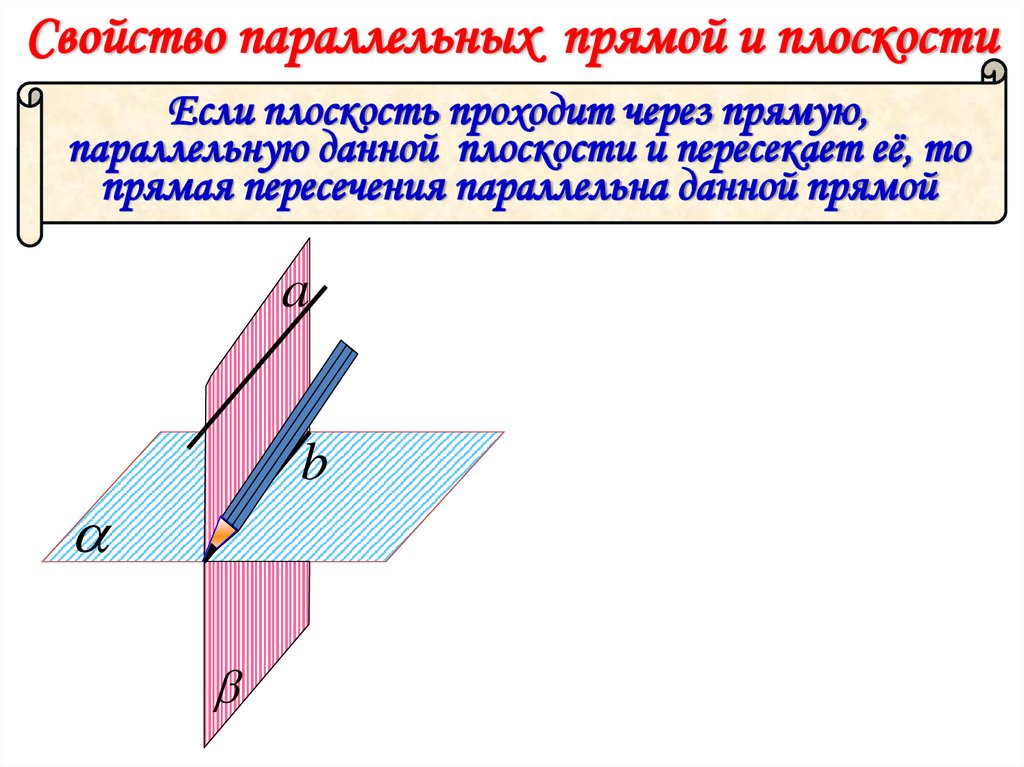
Свойство параллельных прямой и плоскости
Если плоскость проходит через прямую,
параллельную данной плоскости и пересекает её, то
прямая пересечения параллельна данной прямой
a
b

29.

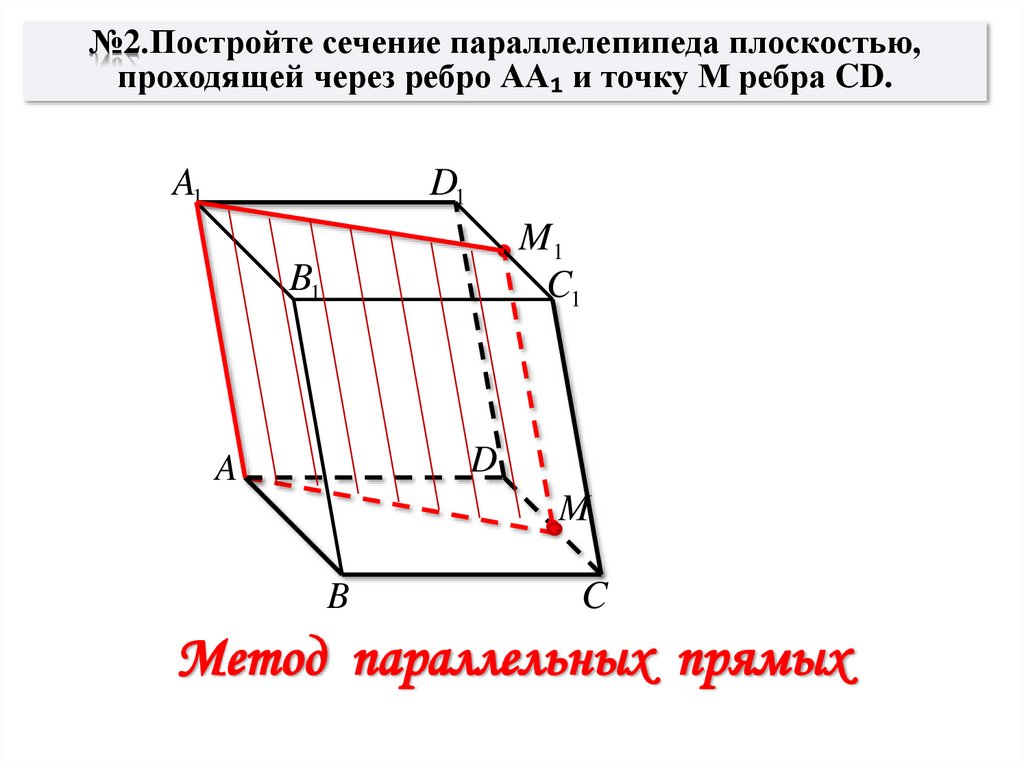
№2.Постройте сечение параллелепипеда плоскостью,
проходящей через ребро АА₁ и точку М ребра CD.
A1
D1
M1
C1
B1
D
A
M
B
C
Метод параллельных прямых

30.

В рассмотренных выше примерах
для того, чтобы найти сечение
многогранника,
выполнялись
построения на основании аксиом
и теорем стереометрии на гранях
этого многогранника. В некоторых
случаях для нахождения сечения
приходится
ряд
построений
проводить вне многогранника.

31.

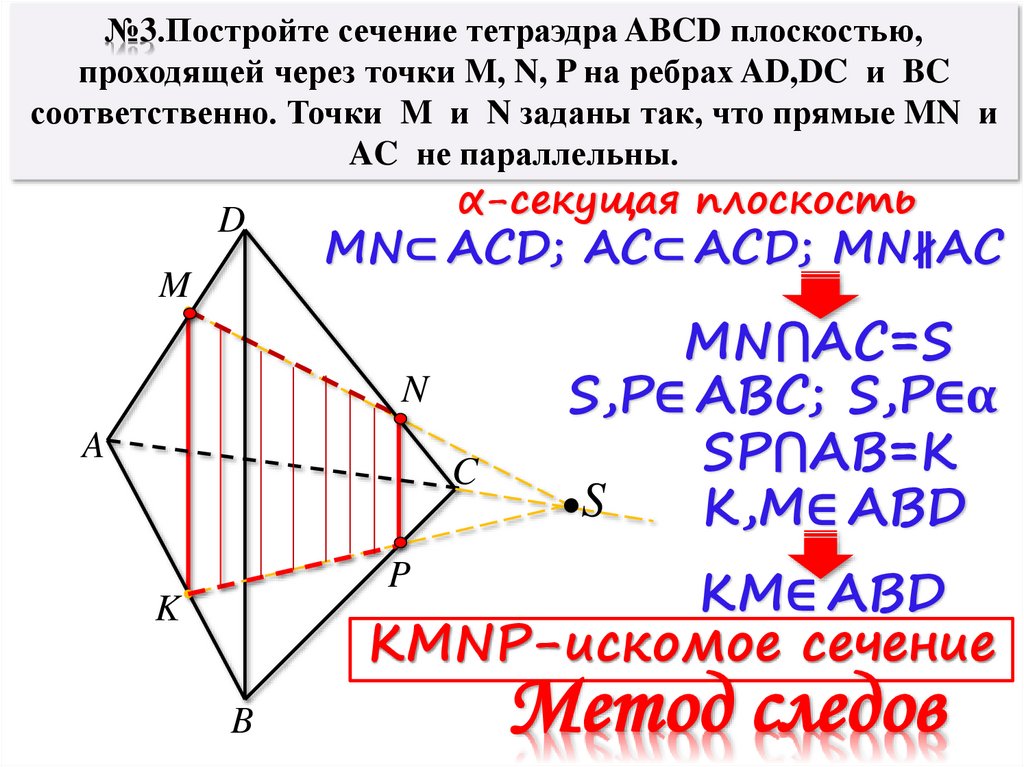
№3.Постройте сечение тетраэдра ABCD плоскостью,
проходящей через точки M, N, P на ребрах AD,DC и BC
соответственно. Точки M и N заданы так, что прямые MN и
AC не параллельны.
D
M
α-секущая плоскость
MN⊂ ACD; AC⊂ ACD; MN∦AC
N
A
C
MN⋂AC=S
S,P∈ ABC; S,P∈