Первый признак треугольника. Доказательство

1.

Автор: Вислогузова И.А.

2.

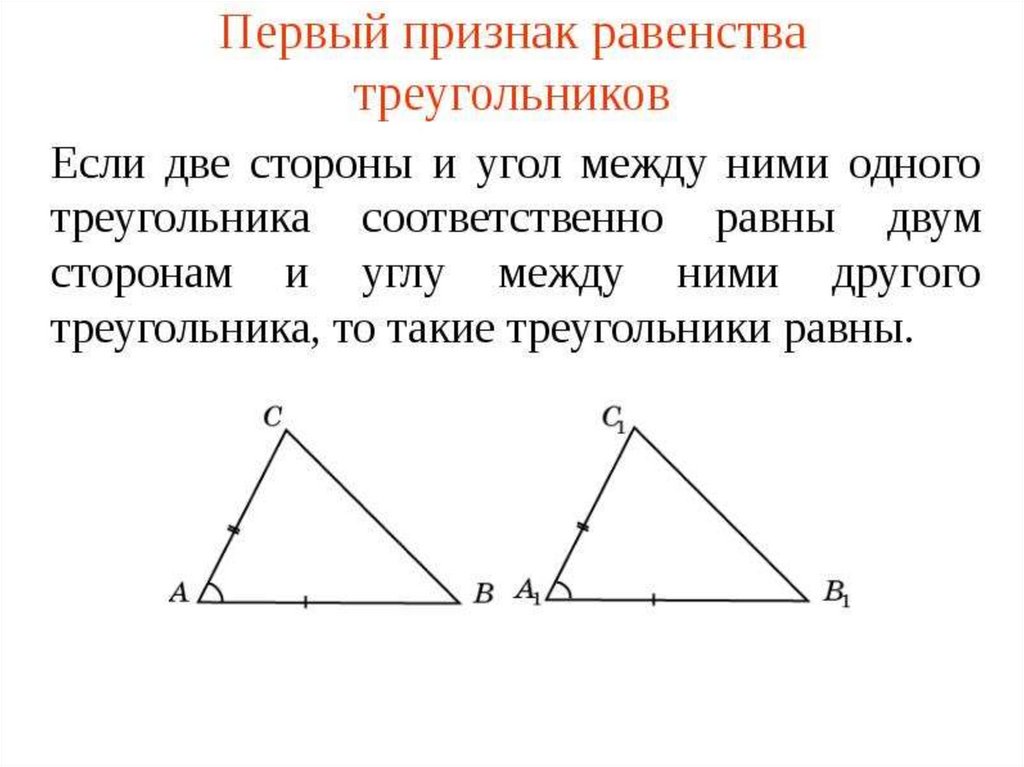
Первый признак

3.

Задача №1
Треугольник ABC - равнобедренный, СD -
биссектриса к основанию АВ.
Докажите, что ACD = BCD

4.

Доказательство:
Докажем, что два треугольника равны по первому
признаку. Из условия мы имеем, что:
1. ∠ACD = ∠DCB (CD - биссектриса);
2. AC = BC ( треугольник АВС - равнобедренный);
3. CD принадлежит обоим треугольникам.
Тогда, треугольники ACD и BCD имеют две равные
стороны и угол между ними.
Поэтому треугольники △ACD и △BCD - равны.

5.

6.

Задача №2
Докажите, что если в треугольнике высота и
биссектриса, проведенные из одной вершины,
равны, то треугольник равнобедренный.

7.

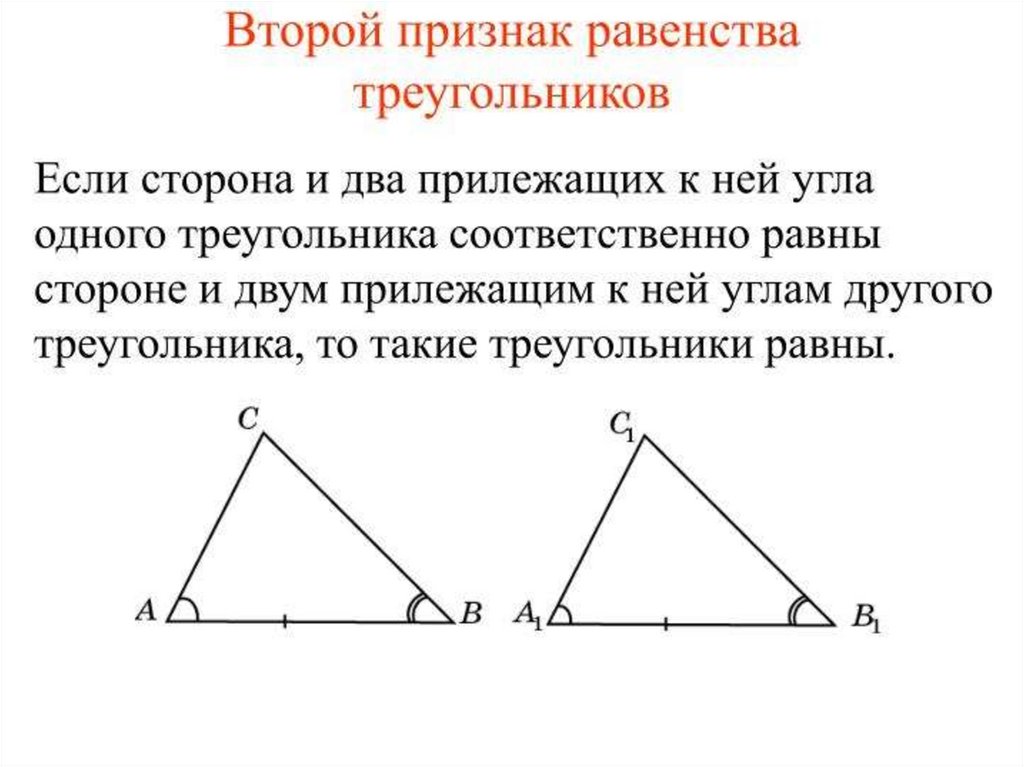
Доказательство
Для того, чтобы доказать, что AC = BC, т.е. △ABC
является равнобедренным, достаточно доказать,
что △APC = △ BPC.
Но △APC = △BPC (по второму признаку) потому
что
1. ∠ACP = ∠BCP (CP - биссектриса)
2. ∠APС = ∠CPB = 90° (CP - высота)
3. CP - общая сторона
Следовательно AC = BC ⇒ ABC - равнобедренный

8.

9.

Задача №3
Дано: АС = ВС, АD = BD,
∠CAD =120
Найти:∠CBD.

10.

Решение

11.

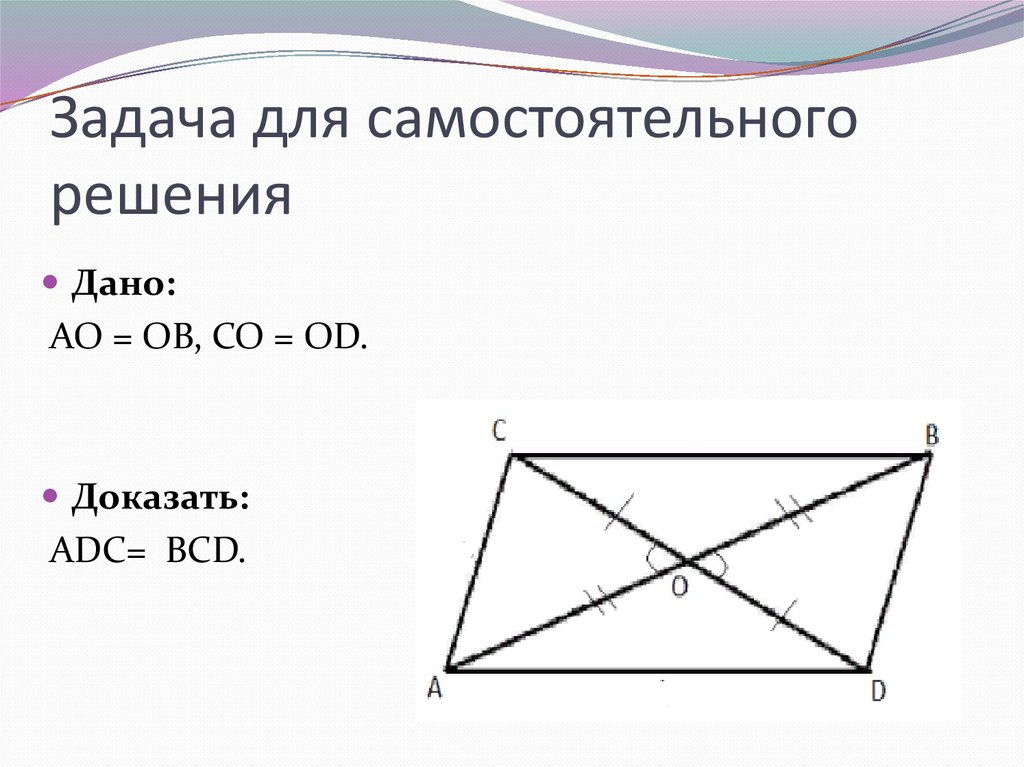
Задача для самостоятельного
решения
Дано:
АО = ОВ, СО = ОD.
Доказать:
ADC= BCD.

12.

Самопроверка
АОС = BOD. Эти треугольники равны по первому
признаку равенства треугольников (СО = OD – по
условию, АО = ОВ – по условию, ∠АОС = ∠DOB –
как вертикальные). Отсюда АС = BD.
ВОС = АOD. Эти треугольники равны по первому
признаку равенства треугольников (СО = OD – по
условию, АО = ОВ – по условию, ∠СОВ = ∠DOА –
как вертикальные). Отсюда ВС = АD.
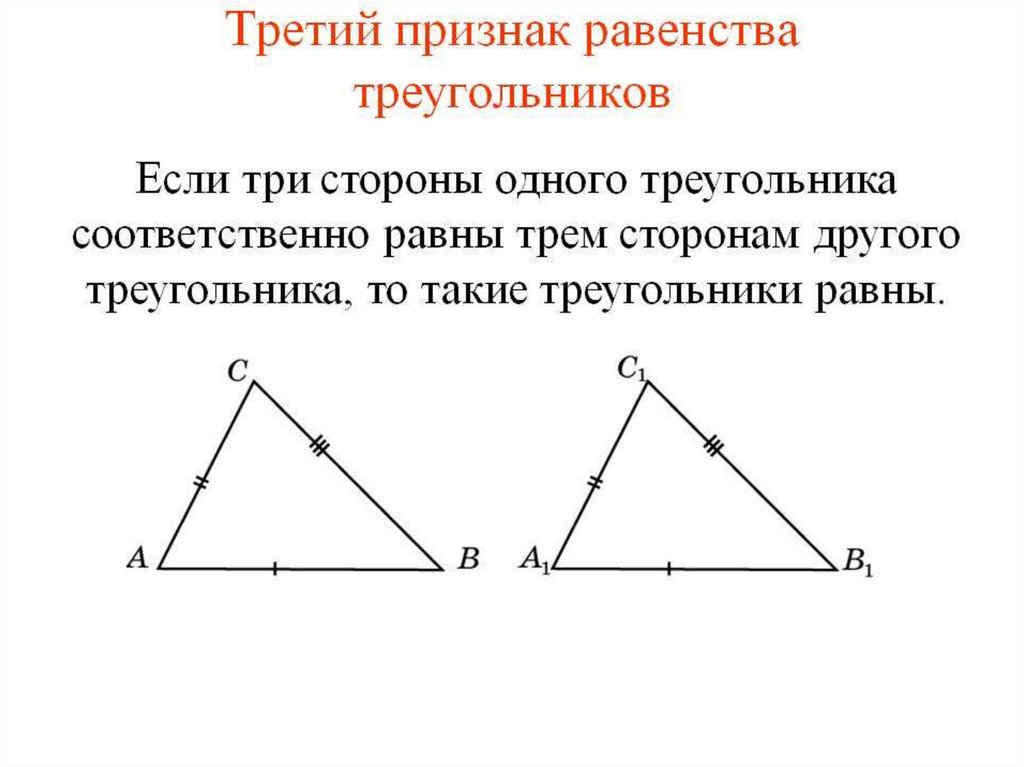
Отсюда треугольники ADC и BCD равны по
третьему признаку равенства треугольников.
Что и требовалось доказать.