Вычисление площадей фигур на клетчатой бумаге

1.

2.

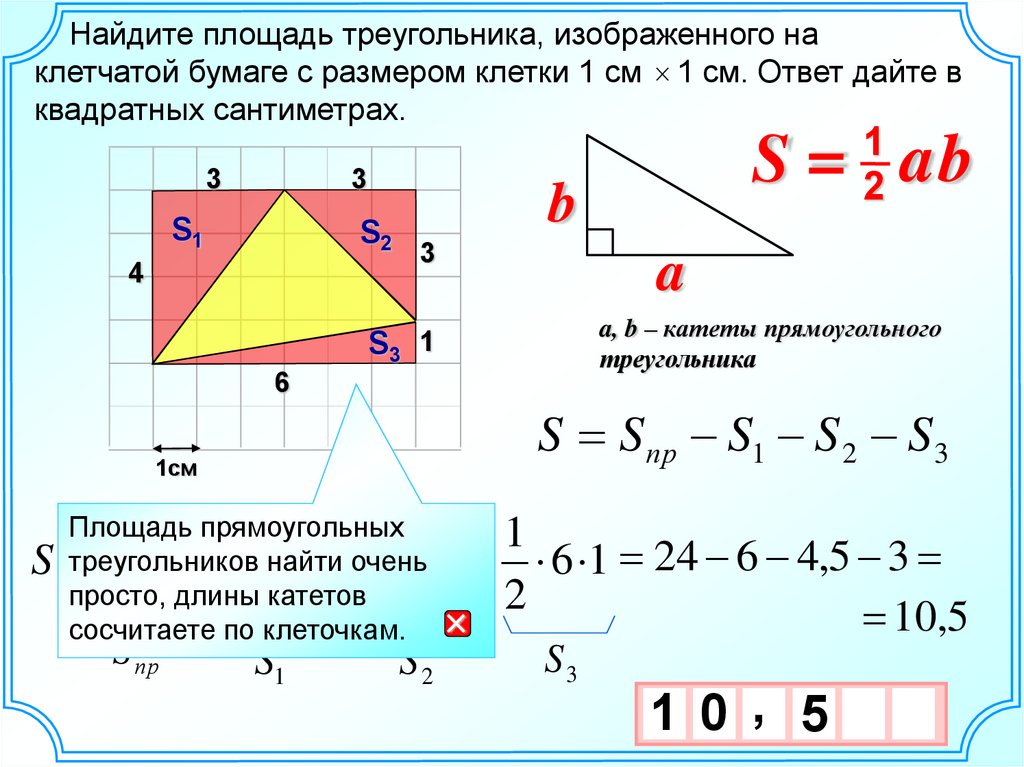
Найдите площадь треугольника, изображенного на
клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в
квадратных сантиметрах.
3
3
S1
S2
4
1
2
S = ab
b
3
a
a, b – катеты прямоугольного
треугольника
S3 1
6
S S пр S1 S 2 S3
1см
Площадь прямоугольных
1
1
1
треугольников
S
6 4 3найти
4 очень
3 3 6 1 24 6 4,5 3
просто, длины
2 катетов2
2
10,5
сосчитаете по клеточкам.
S пр
S1
S2
S3
1 0 , 5
3
10 х
х

3.

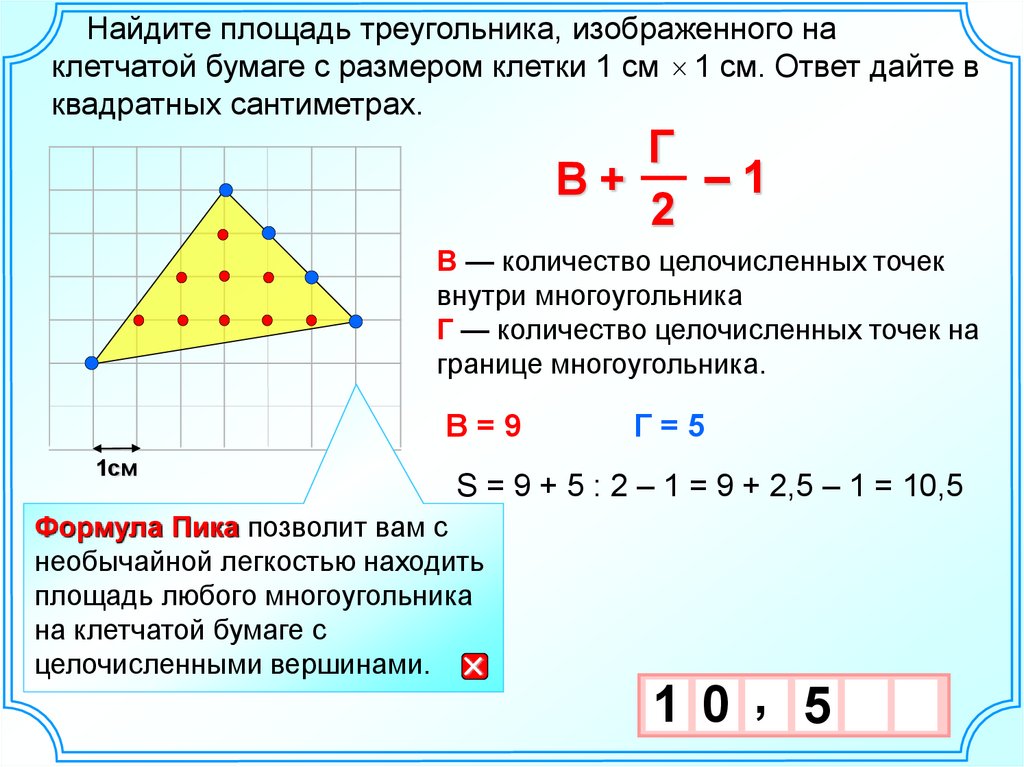
Найдите площадь треугольника, изображенного на
клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в
квадратных сантиметрах.
Г
–1
B+
2
В — количество целочисленных точек
внутри многоугольника
Г — количество целочисленных точек на
границе многоугольника.
В=9
1см
Г=5
S = 9 + 5 : 2 – 1 = 9 + 2,5 – 1 = 10,5
Формула Пика позволит вам с
необычайной легкостью находить
площадь любого многоугольника
на клетчатой бумаге с
целочисленными вершинами.
1 0 , 5
3
10 х
х

4.

Найдите площадь четырёхугольника, изображенного на
клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в
квадратных сантиметрах.
3
2
2
S1
S2
3
1
2
S = ab
b
a
S3
a, b – катеты прямоугольного
4
треугольника
S S пр S1 S 2 S3
1см
1
1
1
S 3 4 3 2 3 2 4 1 12 3 3 2 4
2
2
2
S пр
S1
S2
S3
4
3
10 х
х

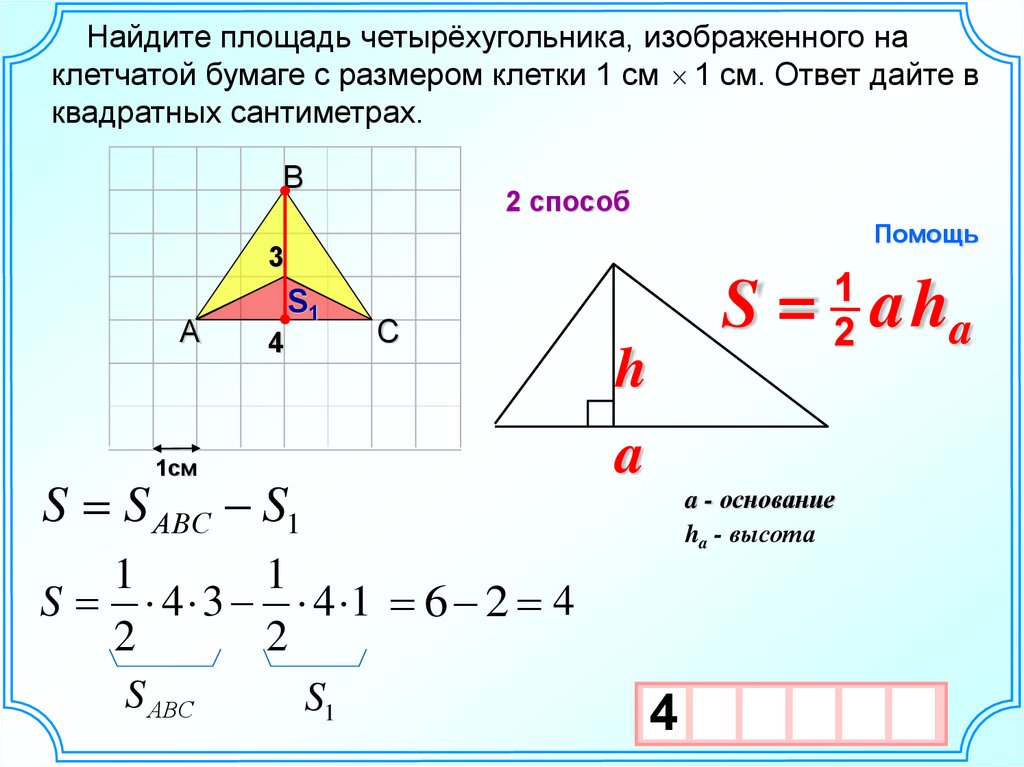
5.

Найдите площадь четырёхугольника, изображенного на
клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в
квадратных сантиметрах.
В
2 способ
Помощь
3
А
S1
4
С
1
2
S = aha
h
a
1см
S S АВС S1
a - основание
ha - высота
1
1
S 4 3 4 1 6 2 4
2
2
S АВС
S1
4
3
10 х
х

6.

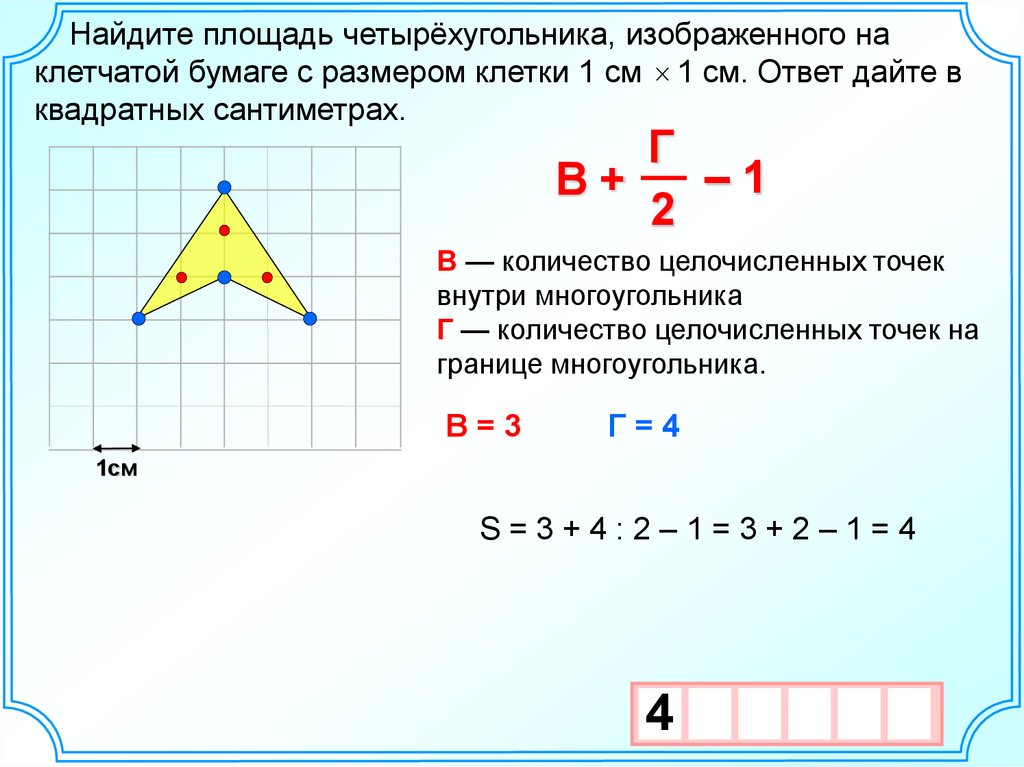
Найдите площадь четырёхугольника, изображенного на
клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в
квадратных сантиметрах.
Г
–1
B+
2
В — количество целочисленных точек
внутри многоугольника
Г — количество целочисленных точек на
границе многоугольника.
В=3
Г=4
1см
S=3+4:2–1=3+2–1=4
4
3
10 х
х

7.

Найдите площадь пятиугольника, изображенного на
клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в
квадратных сантиметрах.
Г
–1
B+
2
В — количество целочисленных точек
внутри многоугольника
Г — количество целочисленных точек на
границе многоугольника.
В = 10
Г = 10
1см
S = 10 + 10 : 2 – 1 = 10 + 5 – 1 = 14
1 4
3
10 х
х

8.

Найдите площадь параллелограмма, изображенного на
клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в
квадратных сантиметрах.
Первым решит задачу тот, кто знает
высота
формулу для вычисления площади
параллелограмма.
Помощь
4
основание
6
1см
S 4 6 24
h
a
S = a ha
a – основание параллелограмма
ha – высота, проведенная к основанию
2 4
3
10 х
х

9.

Найдите площадь параллелограмма, изображенного на
клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в
квадратных сантиметрах.
Помощь
высота
h
a
4
S = a ha
основание
1
1см
В=0
Г = 10
Г
–1
B+
2
S = 0 + 10 : 2 – 1 = 5 – 1 = 4
a – основание параллелограмма
ha – высота, проведенная к основанию
S 1 4 4
4
3
10 х
х

10.

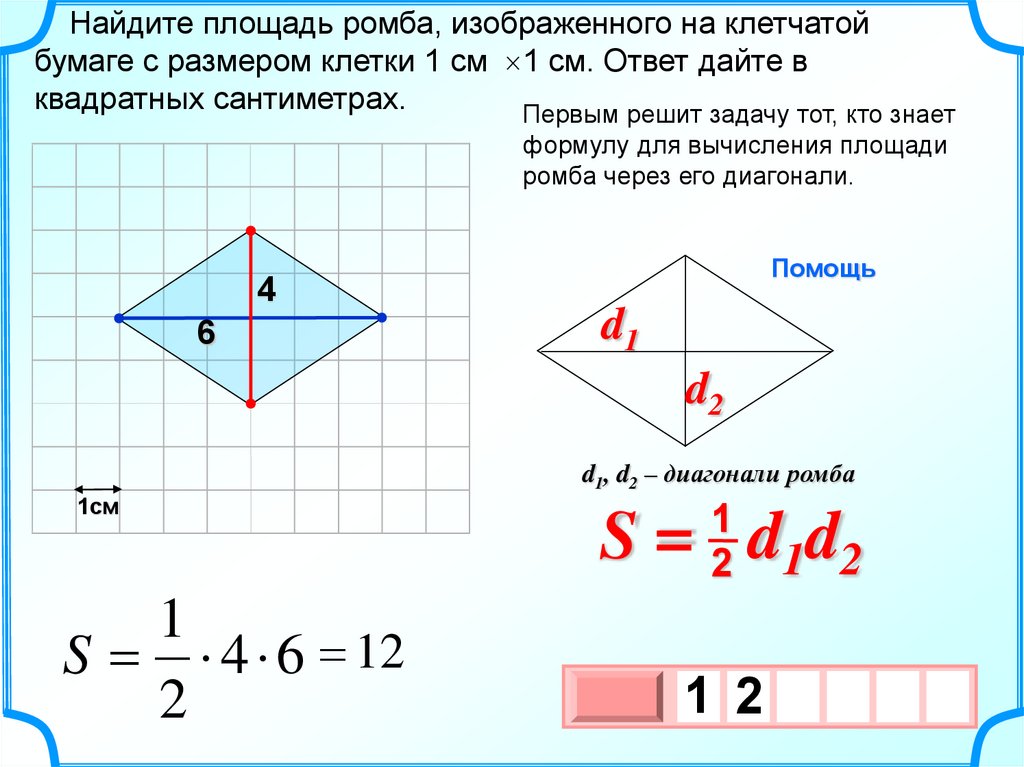
Найдите площадь ромба, изображенного на клетчатой
бумаге с размером клетки 1 см 1 см. Ответ дайте в
квадратных сантиметрах.
Первым решит задачу тот, кто знает
формулу для вычисления площади
ромба через его диагонали.
4
6
Помощь
d1
d2
d1, d2 – диагонали ромба
1см
1
S 4 6 12
2
1
2
S = d1d2
1 2
3
10 х
х

11.

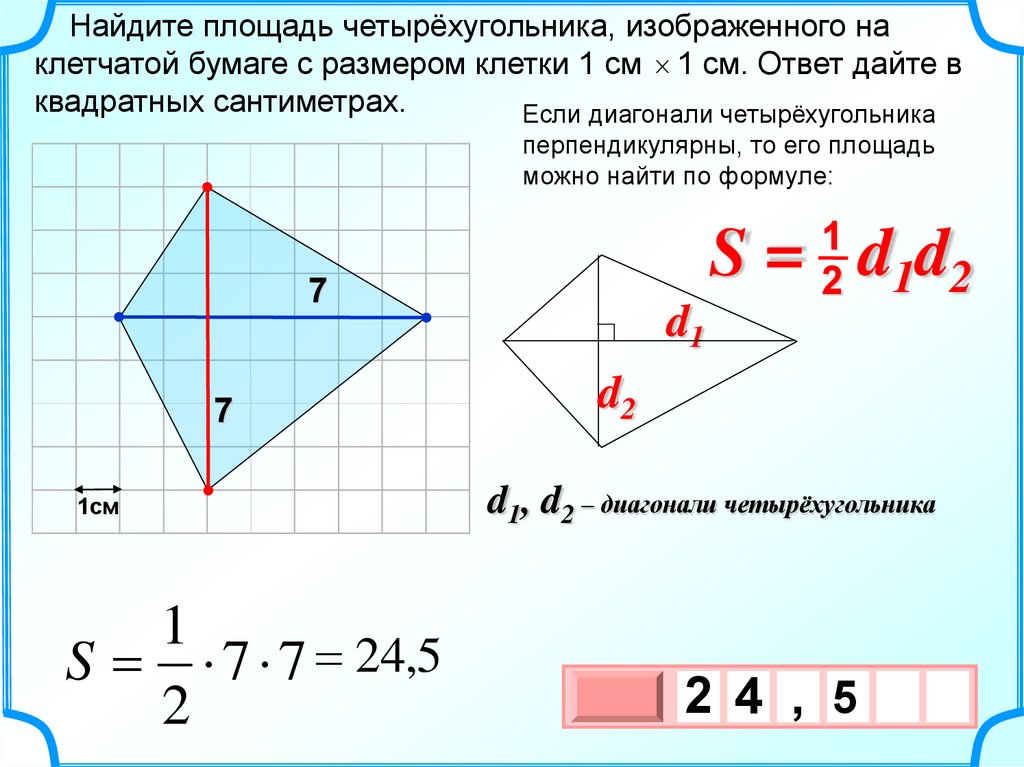
Найдите площадь четырёхугольника, изображенного на
клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в
квадратных сантиметрах.
Если диагонали четырёхугольника
перпендикулярны, то его площадь
можно найти по формуле:
1
2
S = d1d2
7
7
1см
1
S 7 7 24,5
2
d1
d2
d1, d2 – диагонали четырёхугольника
2 4 , 5
3
10 х
х

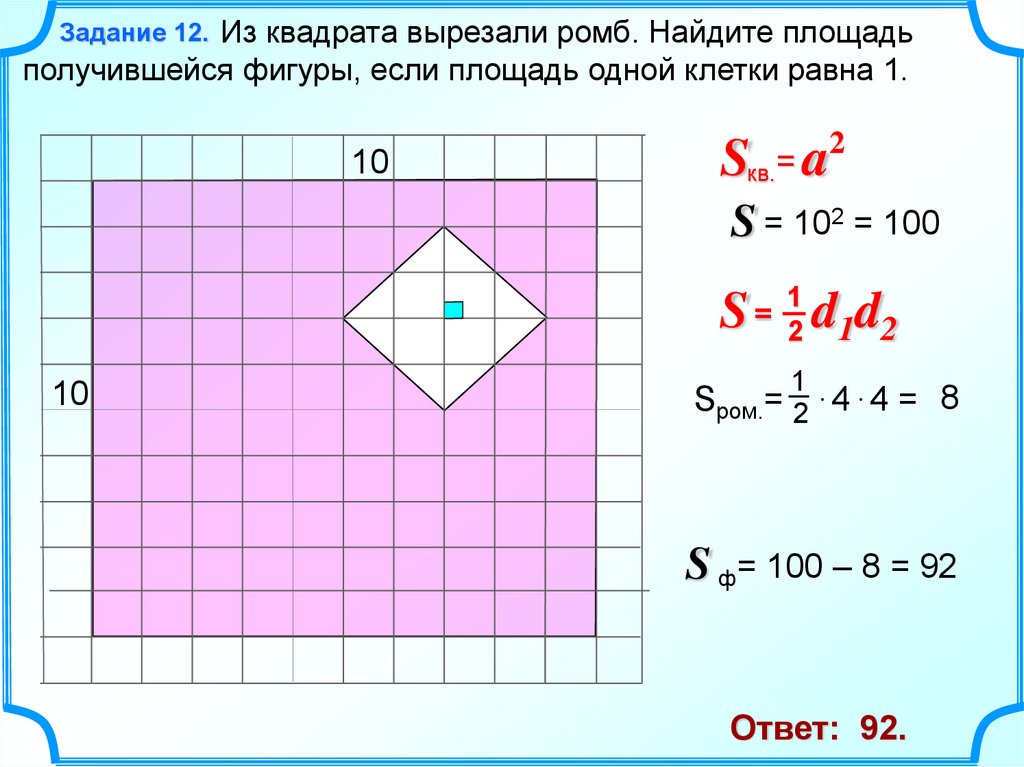
12.

Задание 12. Из квадрата вырезали ромб. Найдите площадь
получившейся фигуры, если площадь одной клетки равна 1.
10
Sкв.= a2
S = 102 = 100
S = 12 d1d2
10
1
Sром.= 2 4 4 = 8
S ф= 100 – 8 = 92
Ответ: 92.

13.

Задание 12. Найдите площадь параллелограмма,
изображённого на клетчатой бумаге со стороной клетки 1.
Sпар. =SABCD–2S1–2S2
S = 12 ab
B
C
S1
24
2
1 10
1
Sпар.= 4 6 –2 2 2 5 –2 2 2 1
S2
Sпар.= 24–10–2 = 12
S2
A
S1
D
Ответ: 12.

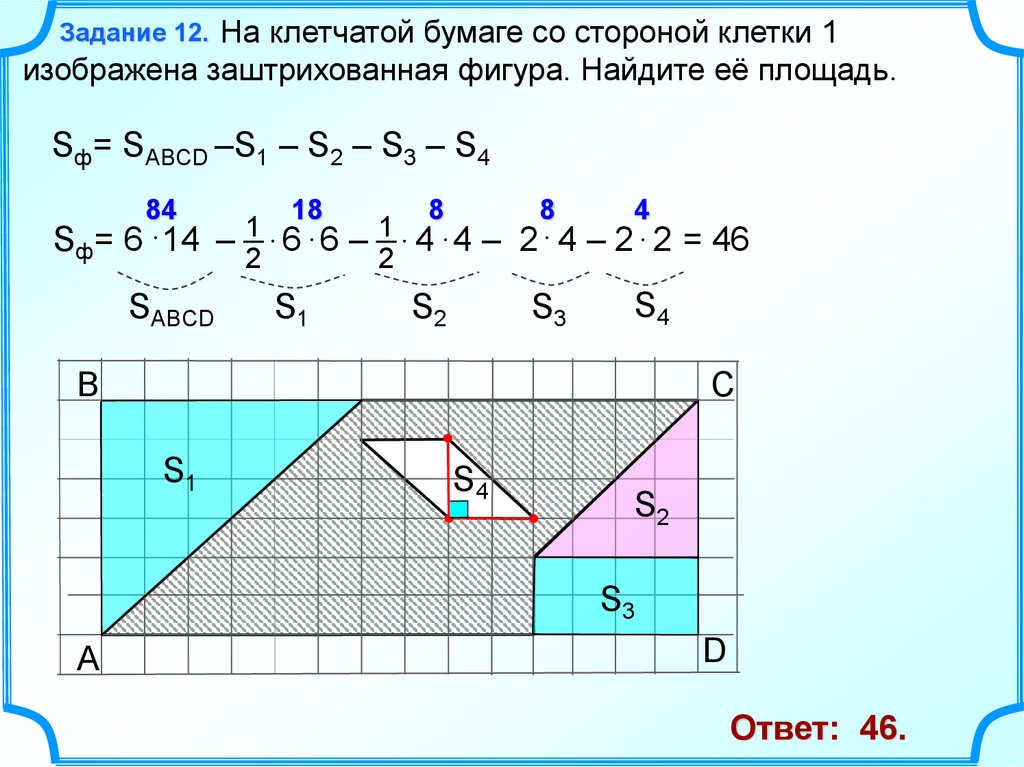
14.

Задание 12. На клетчатой бумаге со стороной клетки 1
изображена заштрихованная фигура. Найдите её площадь.
Sф= SABCD –S1 – S2 – S3 – S4
84
18
8
8
4
1
1
Sф= 6 14 – 6 6 – 4 4 – 2 4 – 2 2 = 46
2
2
SABCD
S1
S2
S3
S4
B
C
S1
S4
S2
S3
A
D
Ответ: 46.

15.

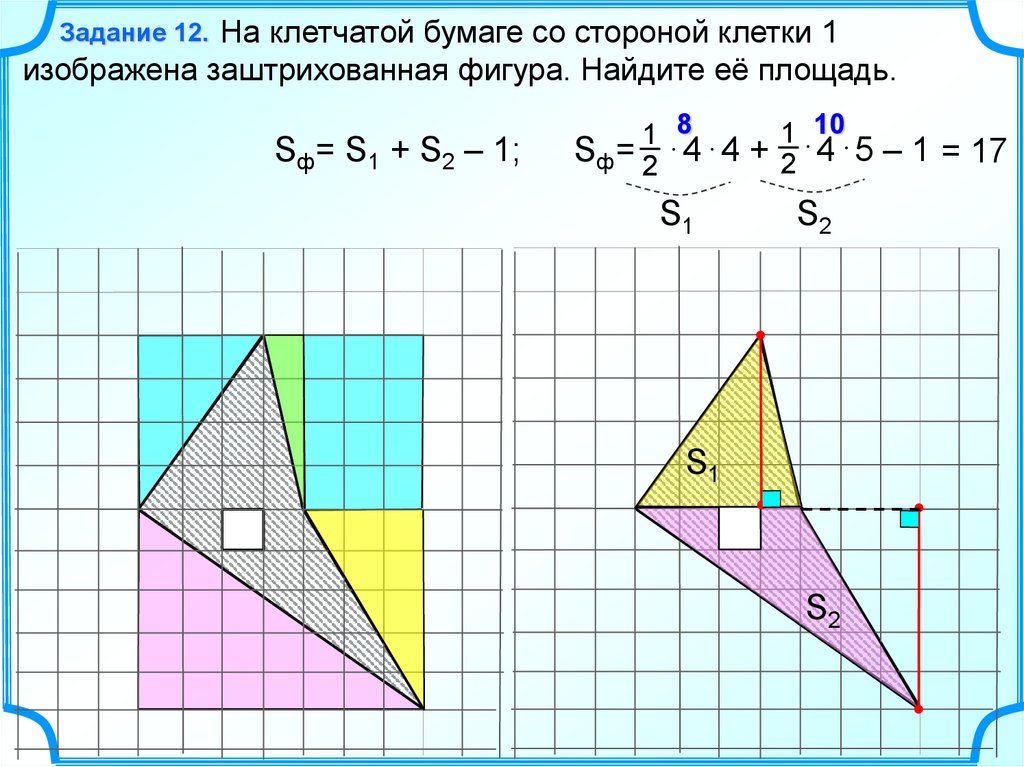
Задание 12. На клетчатой бумаге со стороной клетки 1
изображена заштрихованная фигура. Найдите её площадь.
Sф= S1 + S2 – 1;
1 10
1 8
Sф= 2 4 4 + 2 4 5 – 1 = 17
S1
S2
S1
S2

16.

Способы вычисления площадей фигур на клетчатой
бумаге:
По известным формулам площадей фигур:
треугольника, параллелограмма, трапеции и т.д.
По свойствам площадей, разбивая фигуру на части
или достраивая фигуру.
По формуле Пика.