Вычисление площадей фигур

1.

ГИА - 2016
Открытый банк заданий
по математике
Задача № 11, 12

2.

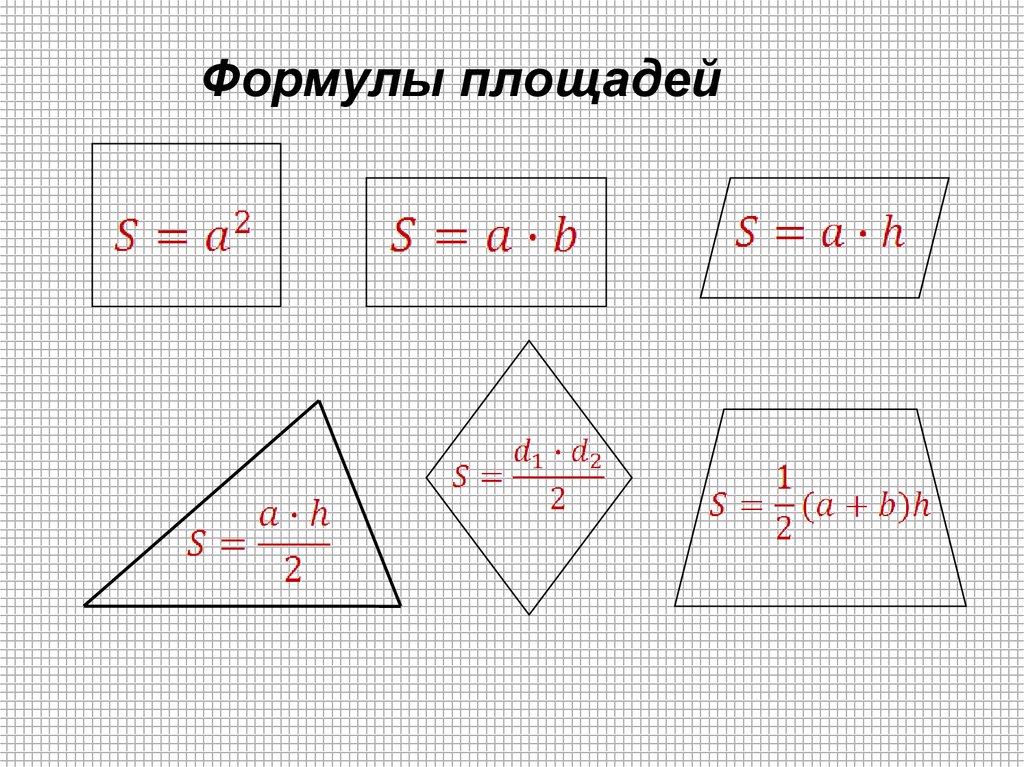
Формулы площадей

3. Найдите площадь фигуры. Ответ дайте в квадратных сантиметрах.

b
а
6 2
S
6
2
Ответ: 6

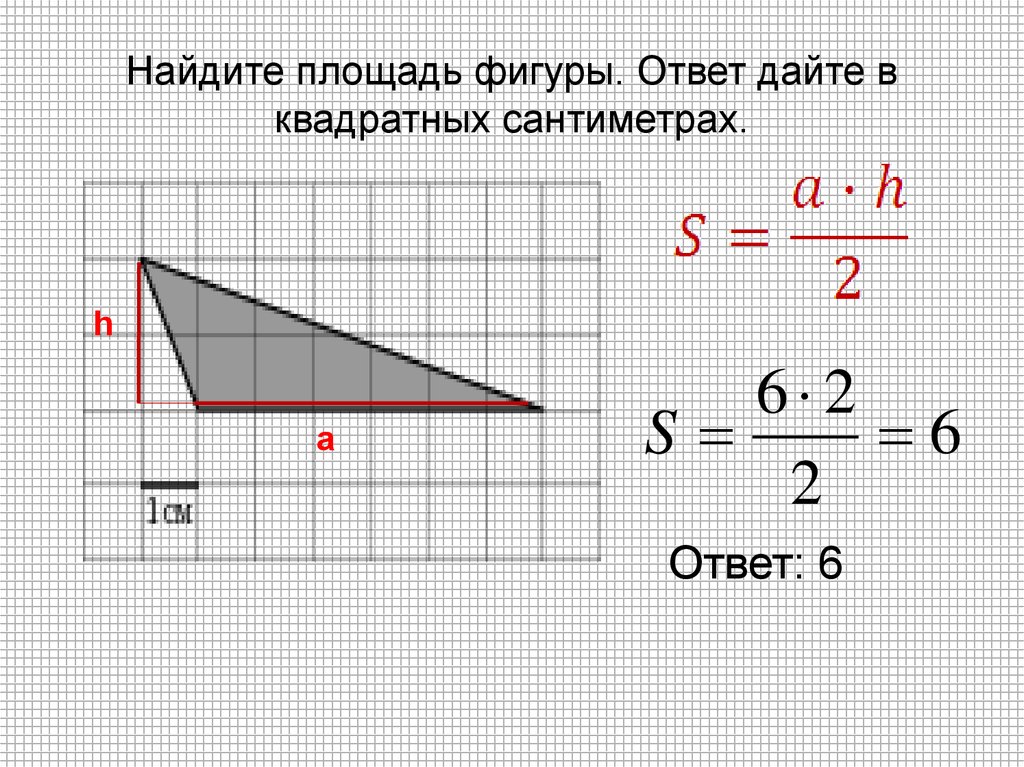
4. Найдите площадь фигуры. Ответ дайте в квадратных сантиметрах.

h
а
6 2
S
6
2
Ответ: 6

5. Найдите площадь фигуры. Ответ дайте в квадратных сантиметрах.

a
h
8 3
S
12
2
Ответ: 12

6. Найдите площадь фигуры. Ответ дайте в квадратных сантиметрах.

h
a
6 2
S
6
2
Ответ: 6

7.

Найдите площадь фигуры. Ответ дайте в
квадратных сантиметрах.
S 7 4 28
Ответ: 28

8.

Найдите площадь фигуры. Ответ дайте в
квадратных сантиметрах.
1
d2
d1
2
6 4
S
12
2
Ответ: 12

9.

Найдите площадь фигуры. Ответ дайте в
квадратных сантиметрах.
a
h
S=
6 1
S
5 17,5
2
b
Ответ: 17,5

10.

Найдите площадь фигуры. Ответ дайте в
квадратных сантиметрах.
b
h
a
9 4
S
5 32,5
2
Ответ: 32,5

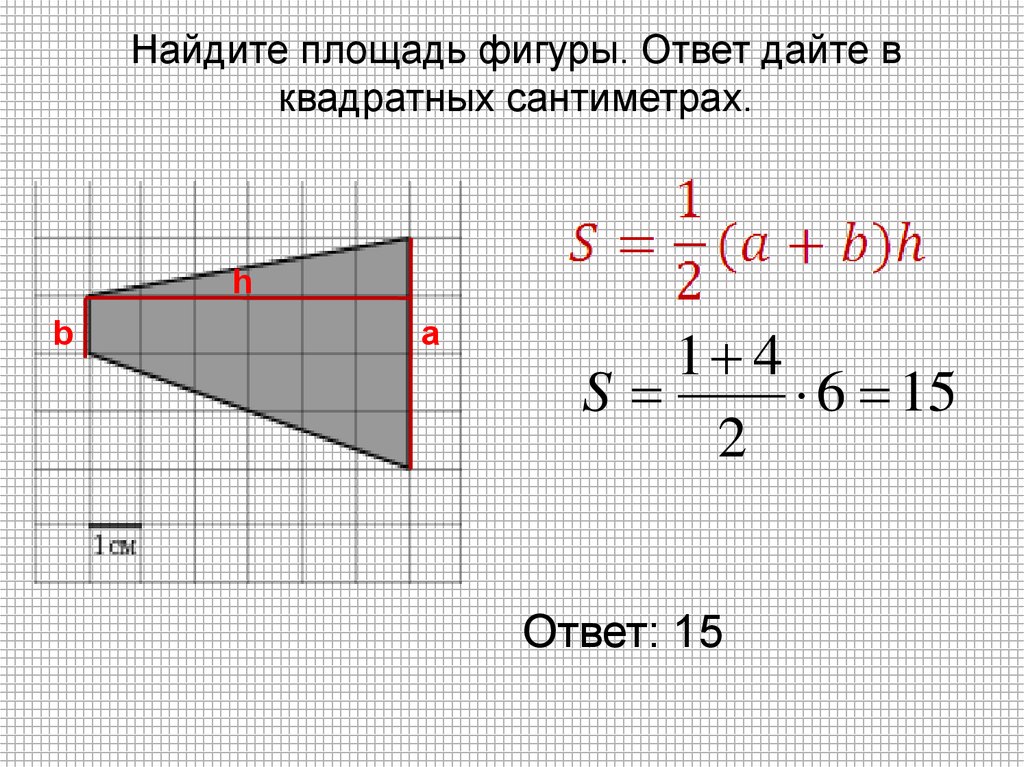
11.

Найдите площадь фигуры. Ответ дайте в
квадратных сантиметрах.
h
b
a
1 4
S
6 15
2
Ответ: 15

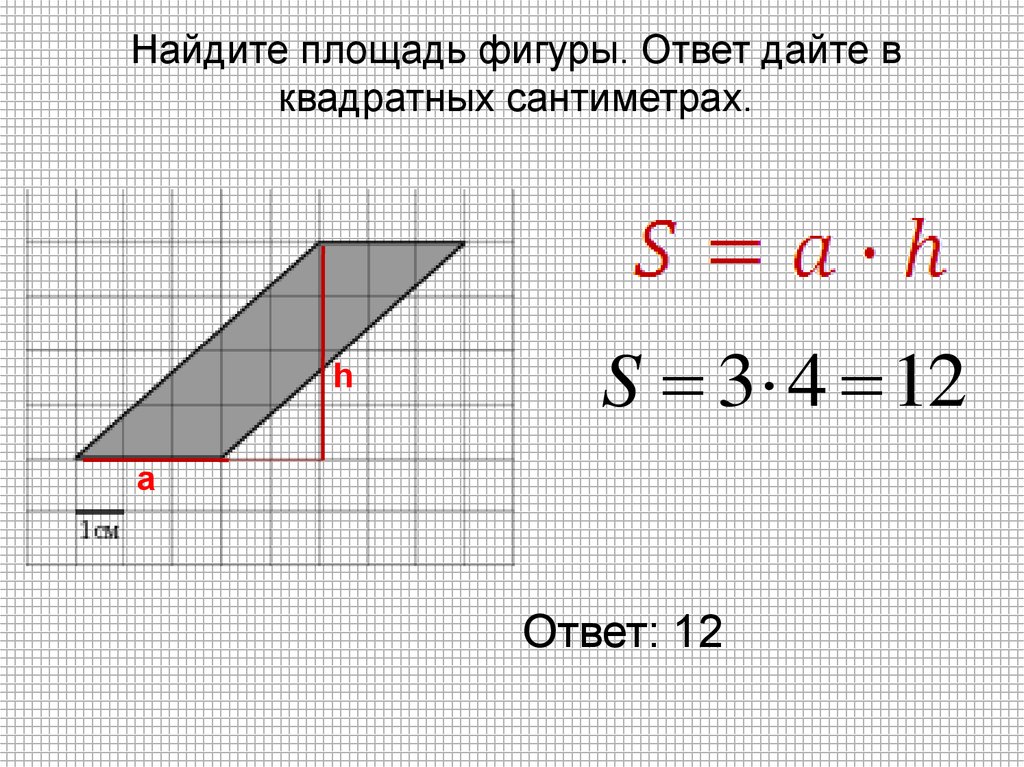
12.

Найдите площадь фигуры. Ответ дайте в
квадратных сантиметрах.
h
S 3 4 12
a
Ответ: 12

13.

2
45
5-3=2
S 5 2 10
Ответ: 10

14.

12
12
6
12
S 6 12 72
Ответ: 72
12

15.

S 18 15 270
Ответ: 270

16.

4
2
4
4
S 2 4 8
Ответ: 8

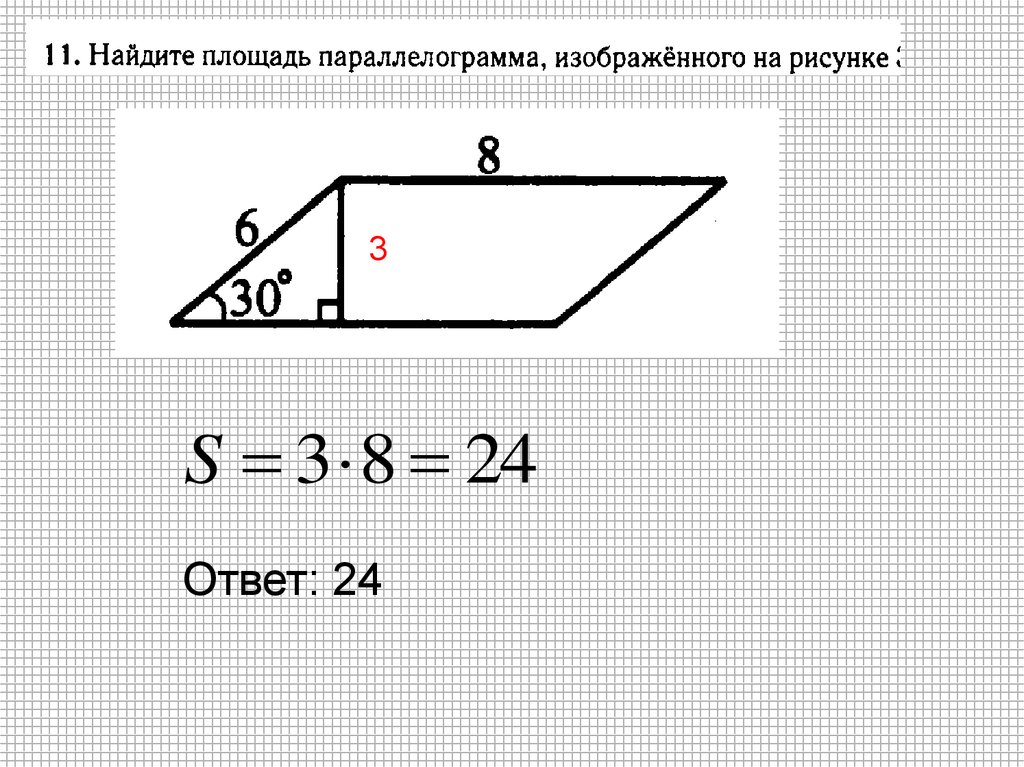
17.

3
S 3 8 24
Ответ: 24

18.

BCD
S BCD
2
k
S ACE
ACE
S BCD
1 2 1
( )
S ACE
3
9
SBCD=90∙1:9=10
SABDE=90-10=80
Ответ: 80

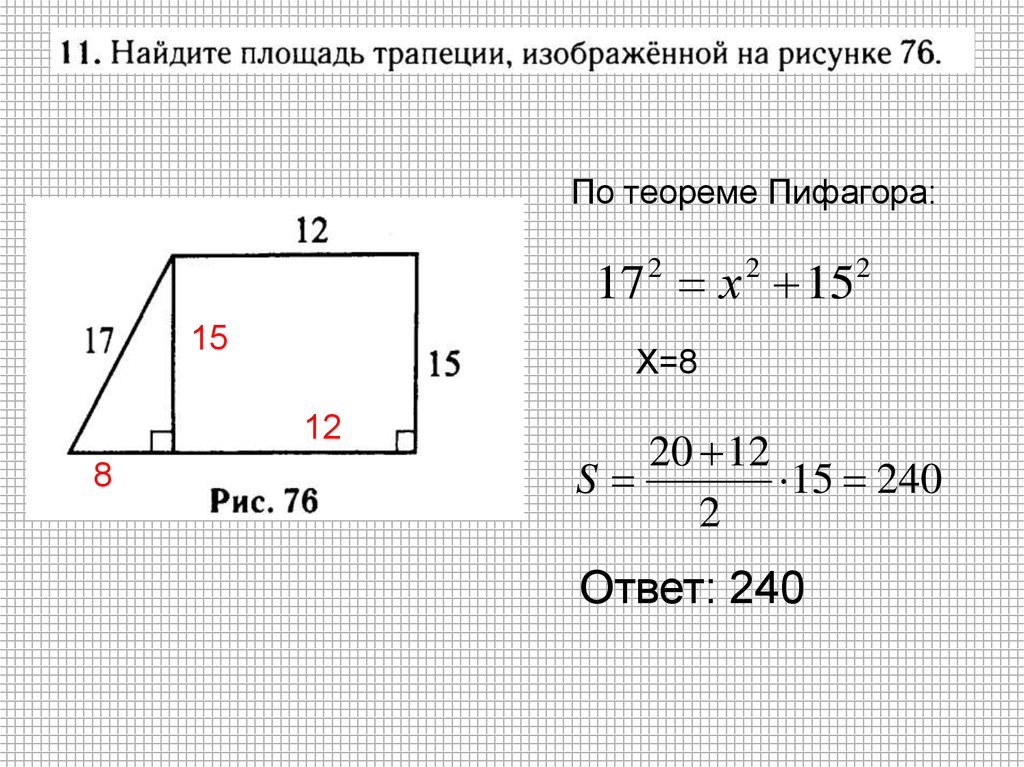
19.

По теореме Пифагора:
17 х 15
2
15
2
Х=8
12
8
2
20 12
S
15 240
2
Ответ: 240

20.

20 6
S
4,8 62,4
2
Ответ: 62,4

21.

х 12
1) Из рисунка видно, что 9,5 - это средняя линия трапеции.
7 х
9,5 Х=12
2
2)
7 12
S
12 114
2
Ответ: 114

22.

8
5
6
По теореме Пифагора:
10 2 х 2 6 2
Х=8
17 5
S
8 88
2
Ответ: 88
6

23.

6
5
5
1) По теореме Пифагора:
61 х 6
2
2
Х=5
8
2) По теореме Пифагора:
10 х 6
2
Х=8
3)
18 5
S
6 69
2
Ответ: 69
2
2

24.

3
1) По теореме Пифагора:
4
К
3
5 х 4
2
2
2
Х=3
2) ABCD равнобедренная, АK=3, KH=4, AD=10
3)
10 4
S
4 28
2
Ответ: 28

25.

1) L – середина AD
3) ABCL - параллелограмм
2) тр-к LCD - равносторонний
4) Проведем диагональ BL
5) Треугольники ABL, BLC и LCD равны, значит и их
площади равны. Площадь треугольника 90:3=30
6) Площадь ABCL составит 30∙2=60
Ответ: 60

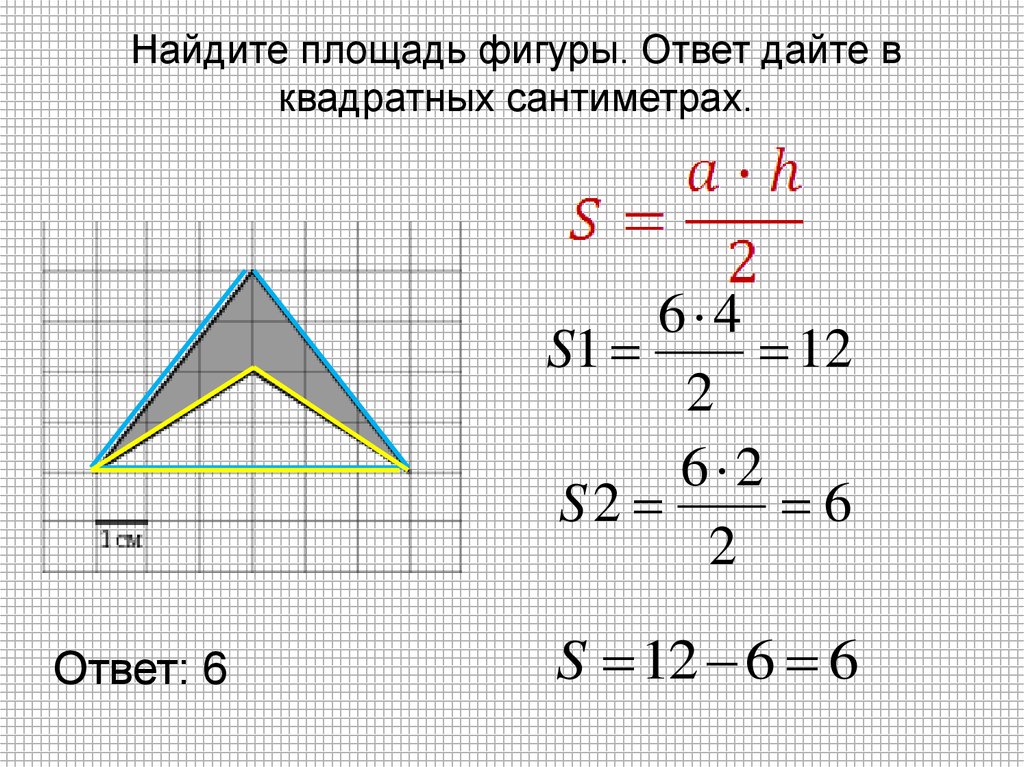
26.

Найдите площадь фигуры. Ответ дайте в
квадратных сантиметрах.
6 4
S1
12
2
6 2
S2
6
2
Ответ: 6
S 12 6 6

27.

Найдите площадь заштрихованной фигуры. Ответ
дайте в квадратных сантиметрах.
S 5 5 25
1
2
3
2 5
S1
5
2
3 3
S2
4,5
2
5 2
S3
5
2
Ответ: 10,5
S 25 5 4,5 5 10,5

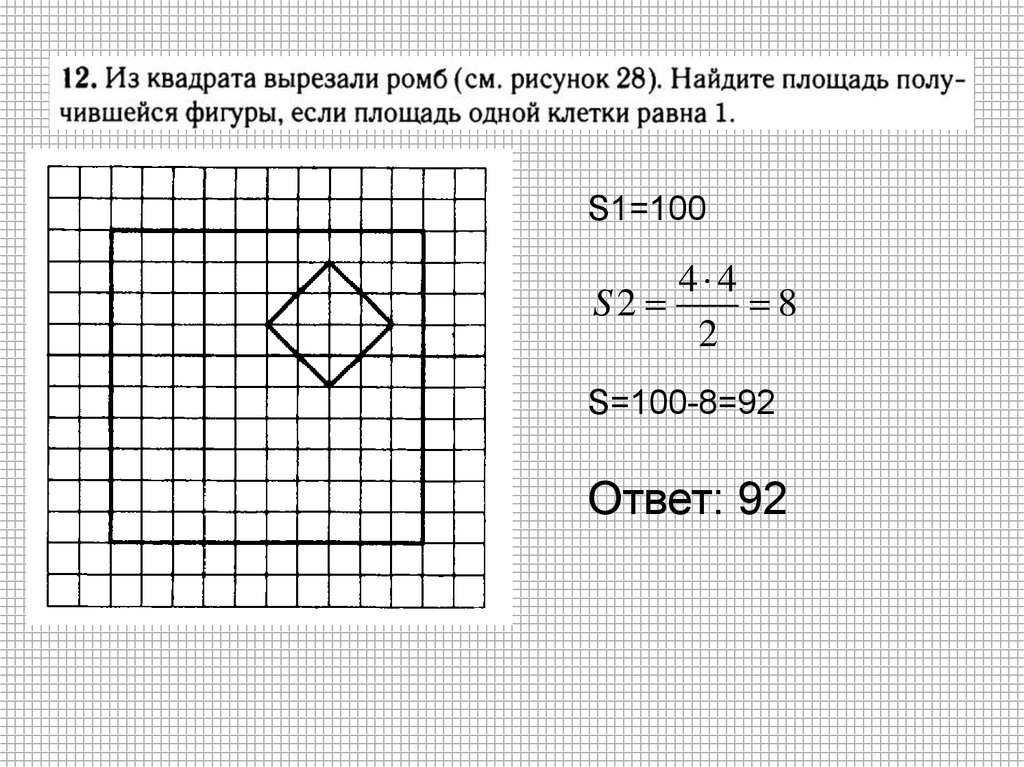
28.

S1=100
4 4
S2
8
2
S=100-8=92
Ответ: 92

29.

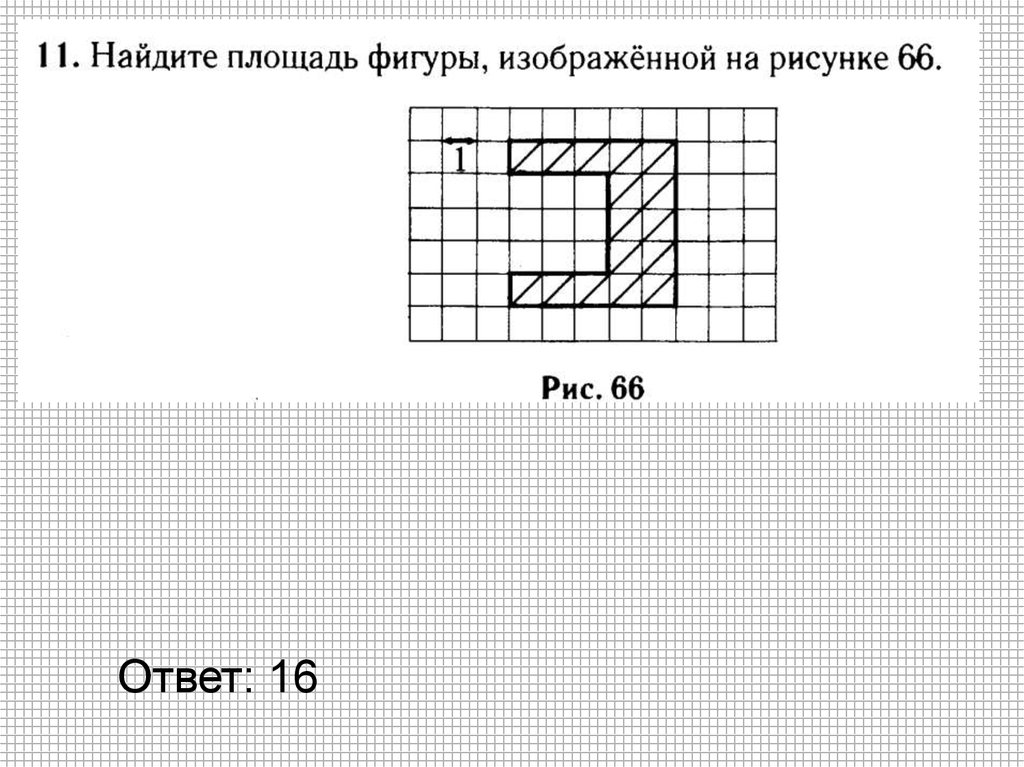
Ответ: 16

30.

S1=8∙4=32
S=32-2-2=28
Ответ: 28
2 2
S 2 S3
2
2

31.

Ответ: 15

32.

Ответ: 45,5

33.

S1=1∙1=1
S2=3∙3=9
1
2
3
S3=10∙3=30
S4=1∙1=1
S=1+9+30+1=41
4
Ответ: 41

34.

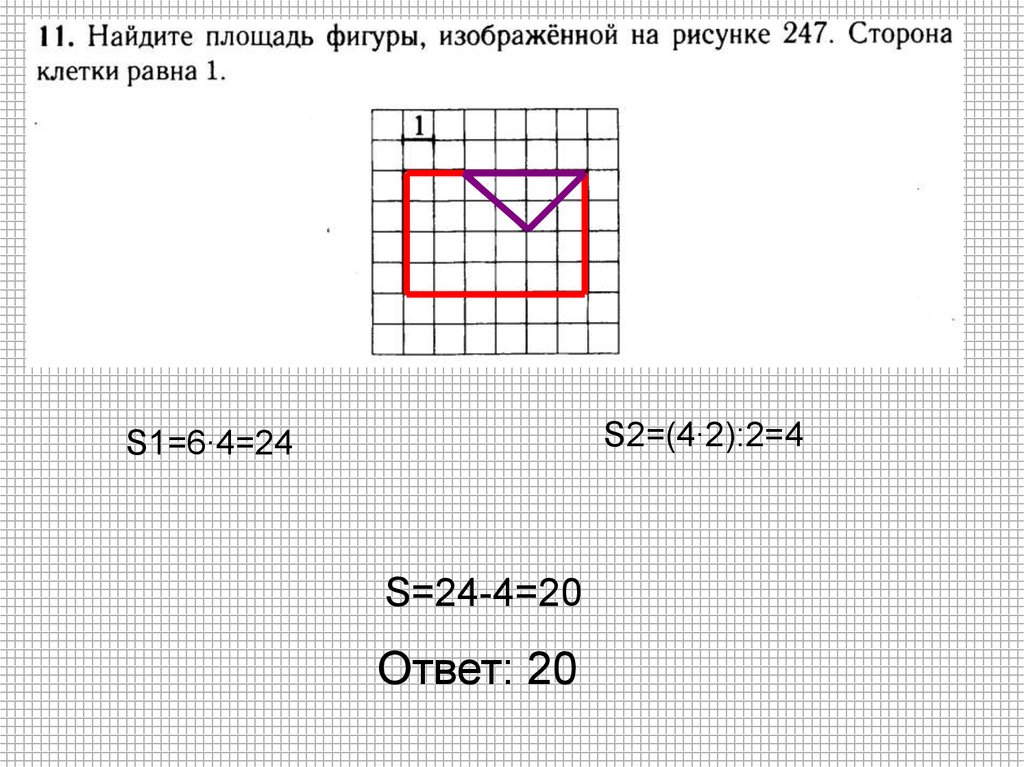
S2=(4∙2):2=4
S1=6∙4=24
S=24-4=20
Ответ: 20

35.

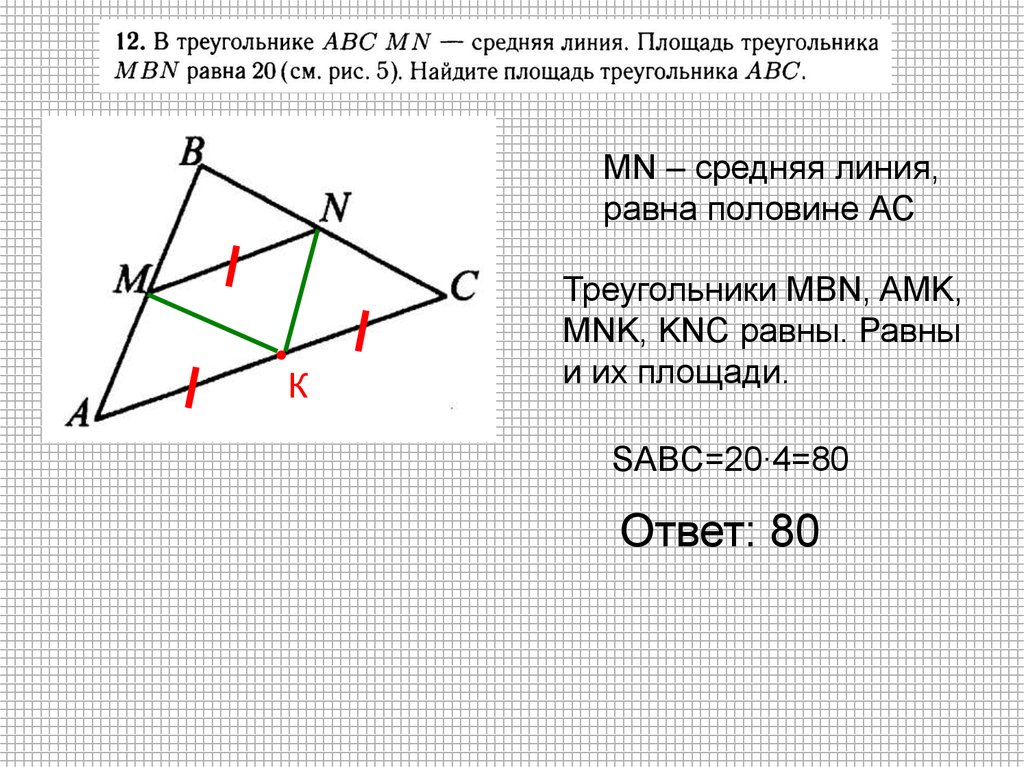
MN – средняя линия,
равна половине АС
К
Треугольники MBN, AMK,
MNK, KNC равны. Равны
и их площади.
SABC=20∙4=80
Ответ: 80