Похожие презентации:
Призма. Прямая и наклонная призма. Параллелепипед. Куб
1.
Призма. Прямая и наклоннаяпризма. Параллелепипед. Куб
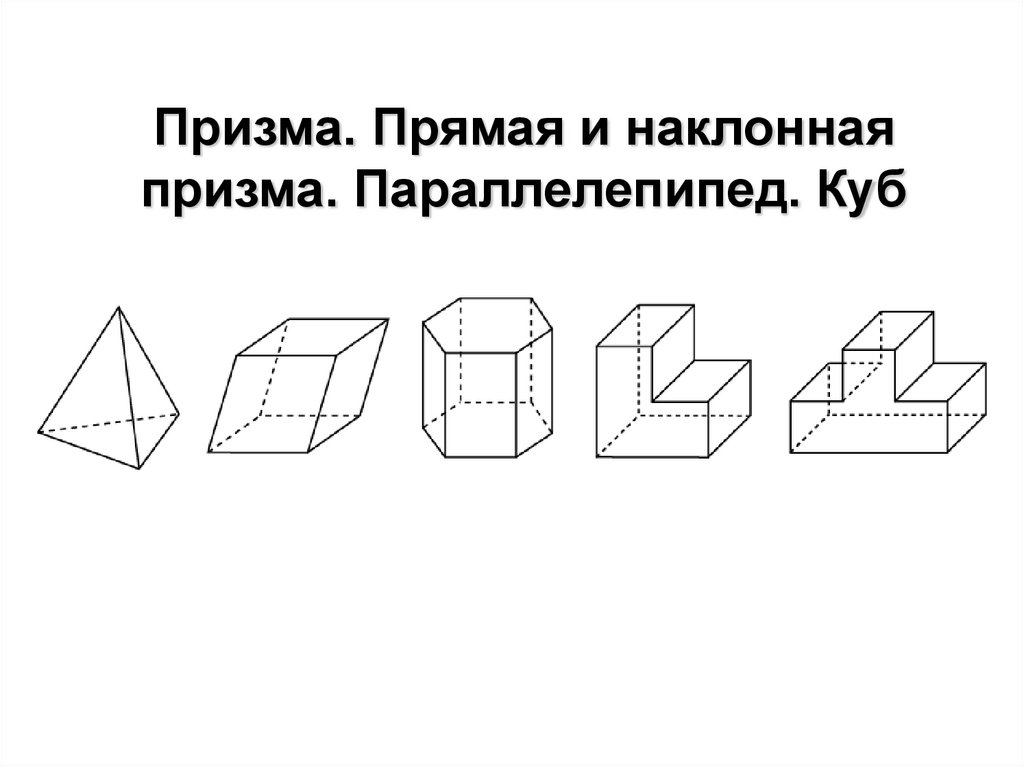
2. Призма. Прямая и наклонная призма. Параллелепипед. Куб
Многогранник – поверхность, составленная измногоугольников и ограничивающая некоторое геометрическое
тело
F
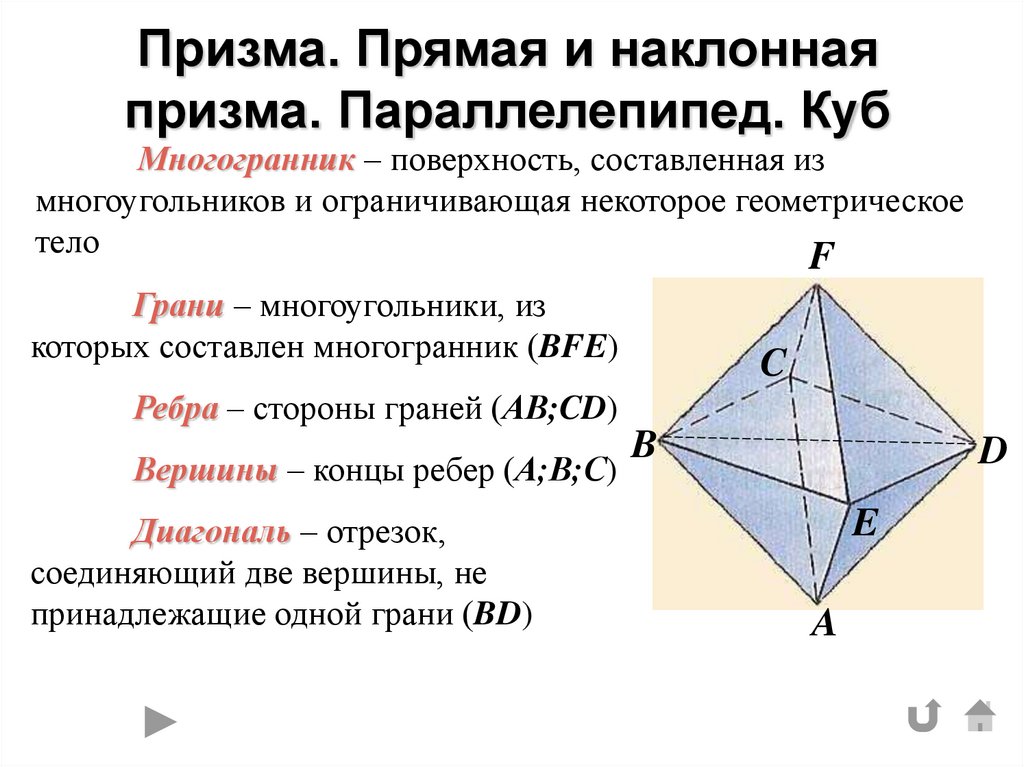
Грани – многоугольники, из
которых составлен многогранник (BFE)
C
Ребра – стороны граней (АВ;CD)
Вершины – концы ребер (А;В;С)
Диагональ – отрезок,
соединяющий две вершины, не
принадлежащие одной грани (BD)
B
D
E
A
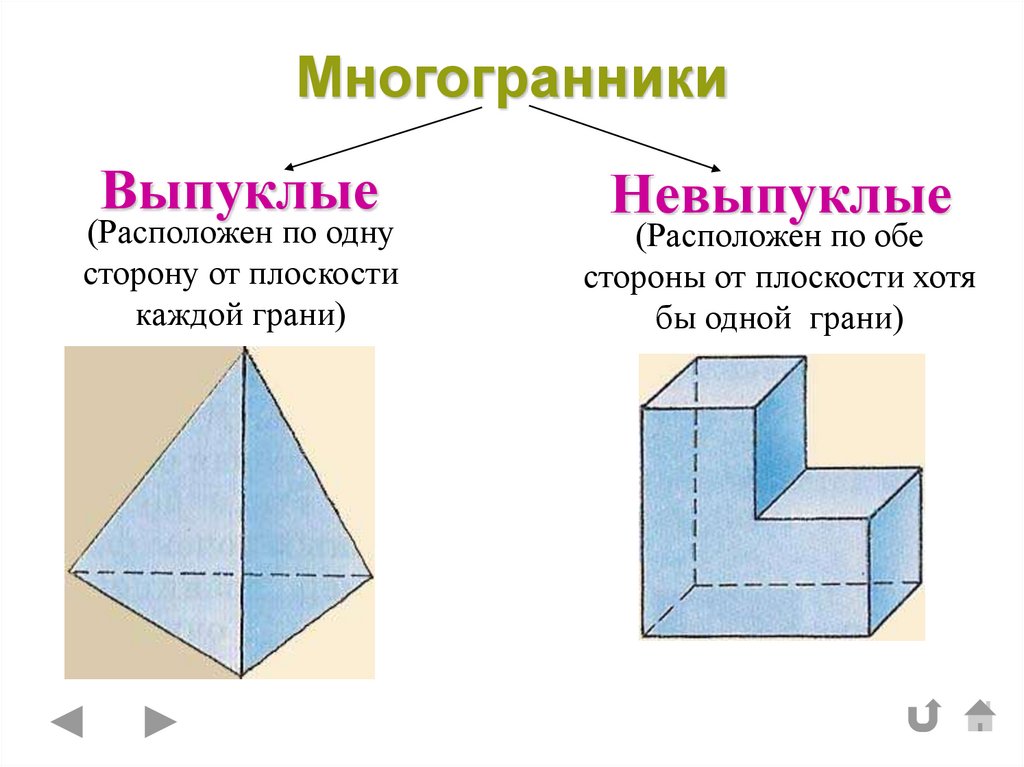
3. Многогранники
Выпуклые(Расположен по одну
сторону от плоскости
каждой грани)
Невыпуклые
(Расположен по обе
стороны от плоскости хотя
бы одной грани)
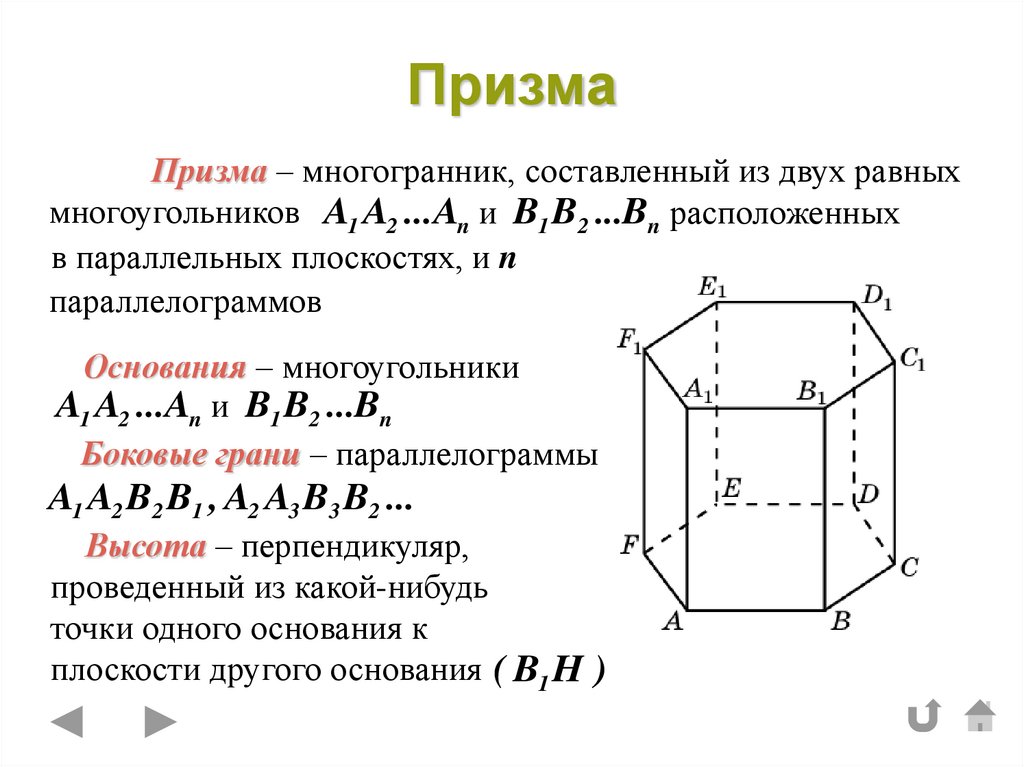
4. Призма
Призма – многогранник, составленный из двух равныхмногоугольников A1 A2 ...An и B1 B2 ...Bn расположенных
в параллельных плоскостях, и n
параллелограммов
Основания – многоугольники
A1 A2 ...An и B1 B2 ...Bn
Боковые грани – параллелограммы
A1 A2 B2 B1 , A2 A3 B3 B2 ...
Высота – перпендикуляр,
проведенный из какой-нибудь
точки одного основания к
плоскости другого основания ( B1 H )
H
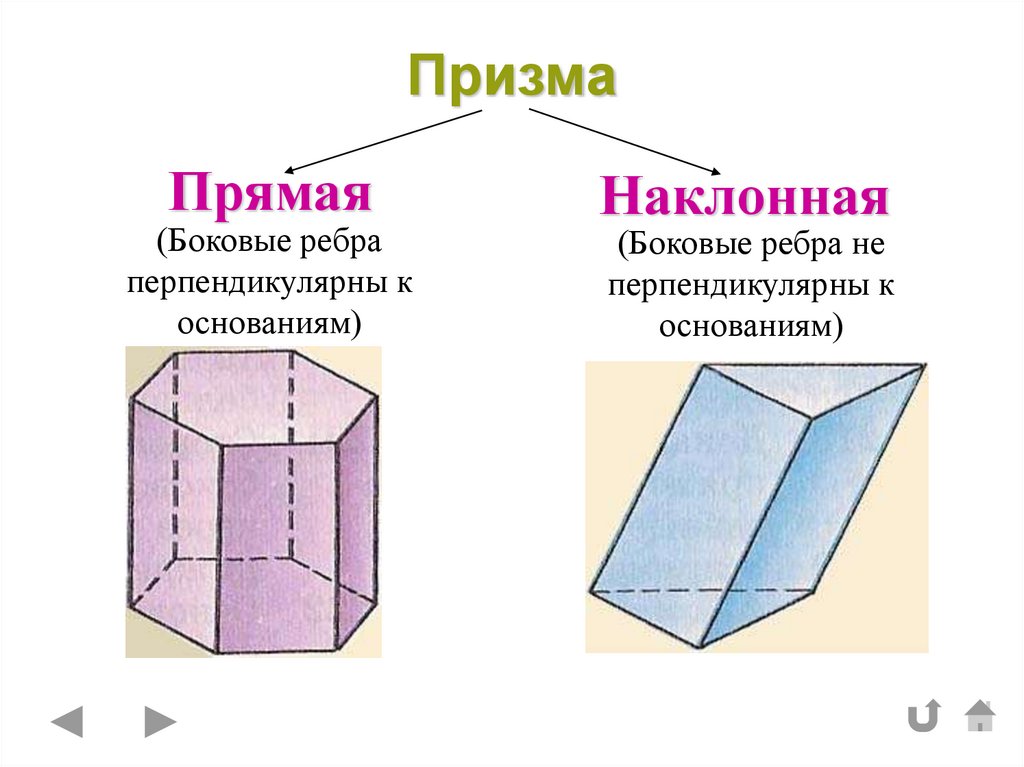
5. Призма
Прямая(Боковые ребра
перпендикулярны к
основаниям)
Наклонная
(Боковые ребра не
перпендикулярны к
основаниям)
6. Площадь поверхности призмы
Площадь полной Площадь боковойповерхности
поверхности
(Сумма площадей всех
граней)
(Сумма площадей боковых
граней)
S ПОЛН S БОК 2 SОСН
7. Площадь боковой поверхности прямой призмы
Теорема: площадь боковой поверхности прямойпризмы равна произведению периметра основания на
высоту призмы
B3
Доказательство:
S БОК S A1 A2 B2 B1 S A2 A3 B3 B2 ... S An A1 B1 Bn
B2
Bn
B1
A1 B1 A2 B2 ... An Bn h
S БОК h A1 A2 h A2 A3 ... h An A1
S БОК h( A1 A2 A2 A3 ... An A1 ) Ph
S БОК Ph
A3
A2
A1
An







 Математика
Математика








