Похожие презентации:
Многоугольники. Ломаная, ее элементы
1.
Многоугольники2.
Ломаная, ее элементыФигура на рисунке составлена из
отрезков АВ, ВС, CD, DE, EF, FS,
ST, TR.
Отрезки АВ и ВС, ВС и CD и т.п.
называются смежными.
Смежные отрезки не лежат на
одной прямой.
Данная фигура называется
ломаной.
Отрезки АВ, ВС, CD, DE, EF, FS, ST, TR называются
звеньями ломаной.
Концы отрезков - точки А, В, C, D, E, F, S, T и R
называются вершинами ломаной.
Точки А и R называются концами ломаной.
Сумма длин всех звеньев называется длиной ломаной.
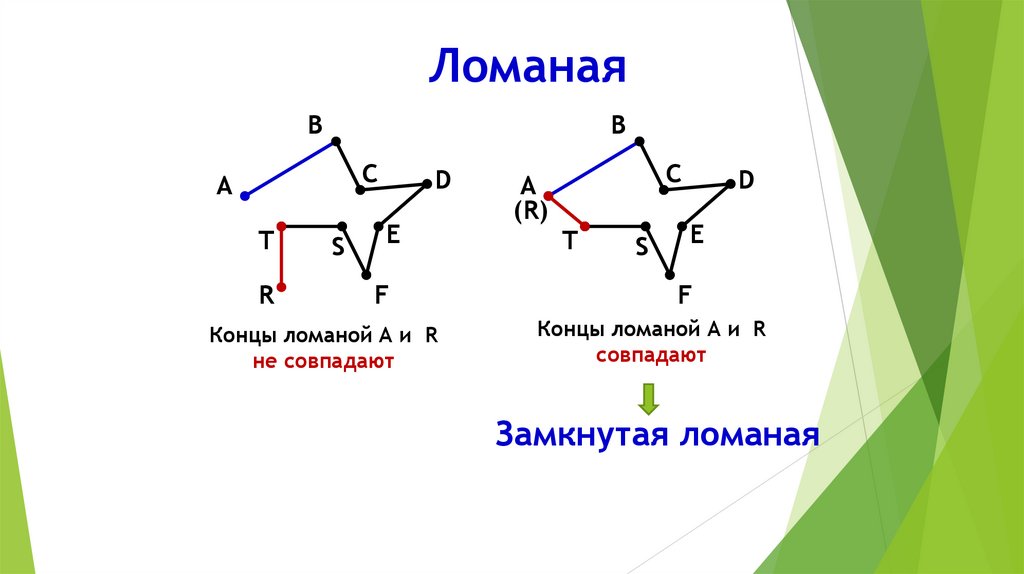
3.
ЛоманаяB
B
C
А
T
R
S
D
E
F
Концы ломаной А и R
не совпадают
C
А
(R)
T
S
D
E
F
Концы ломаной А и R
совпадают
Замкнутая ломаная
4.
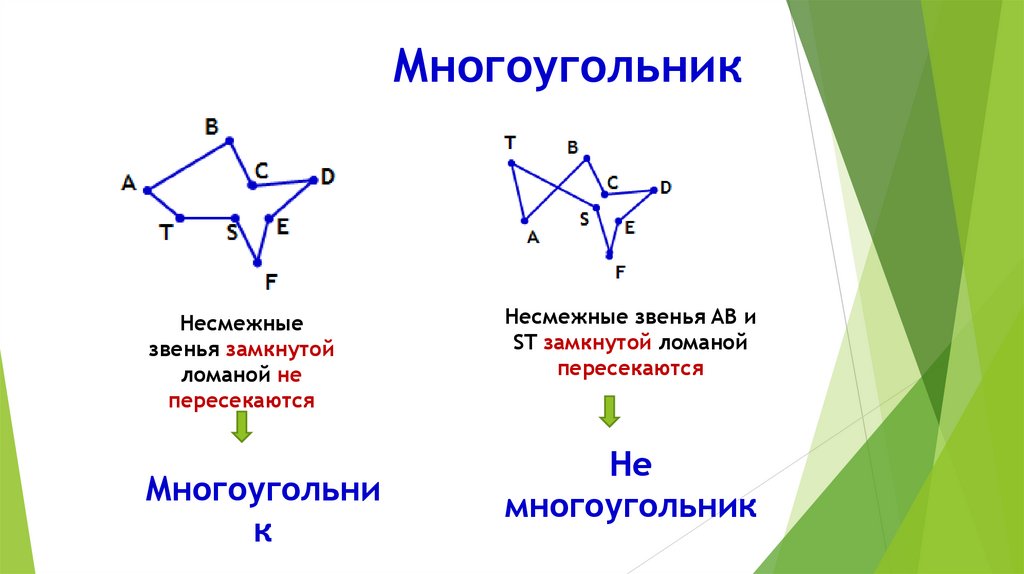
МногоугольникНесмежные
звенья замкнутой
ломаной не
пересекаются
Многоугольни
к
Несмежные звенья AB и
ST замкнутой ломаной
пересекаются
Не
многоугольник
5.
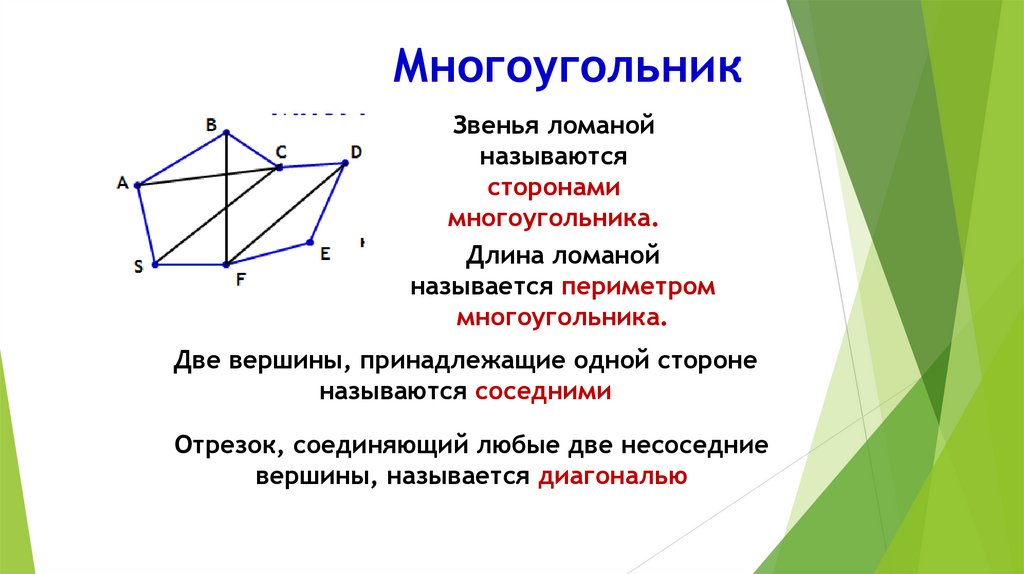
МногоугольникЗвенья ломаной
называются
сторонами
многоугольника.
Длина ломаной
называется периметром
многоугольника.
Две вершины, принадлежащие одной стороне
называются соседними
Отрезок, соединяющий любые две несоседние
вершины, называется диагональю
6.
а)б)
в)
г)
е)
д)
е)
з)
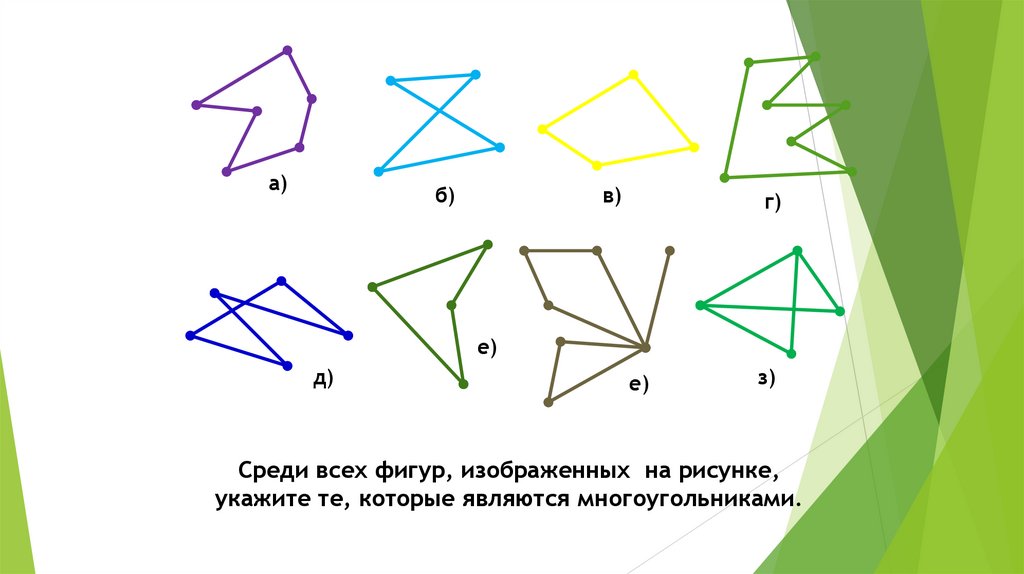
Среди всех фигур, изображенных на рисунке,
укажите те, которые являются многоугольниками.
7.
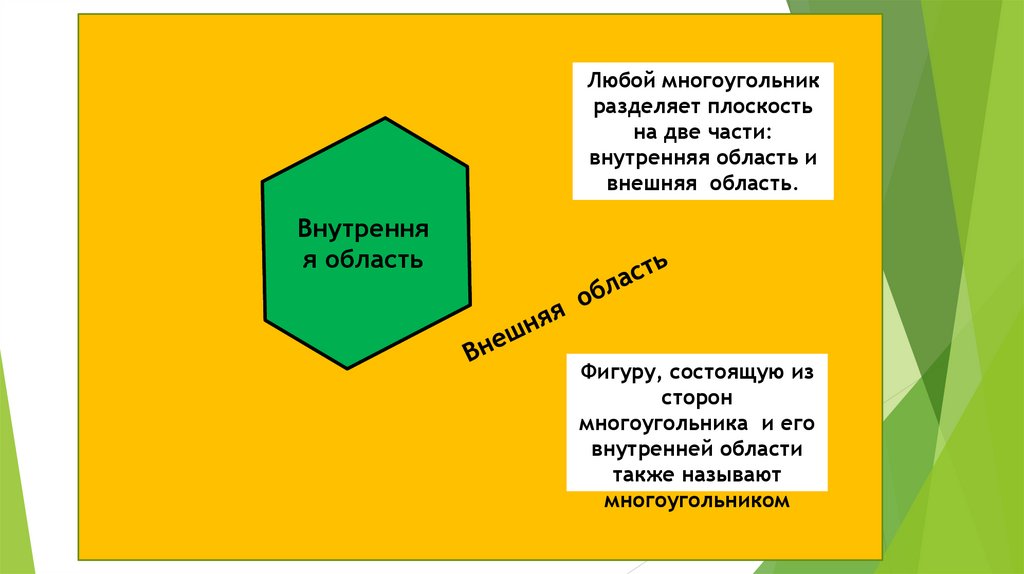
Любой многоугольникразделяет плоскость
на две части:
внутренняя область и
внешняя область.
Внутрення
я область
Фигуру, состоящую из
сторон
многоугольника и его
внутренней области
также называют
многоугольником
8.
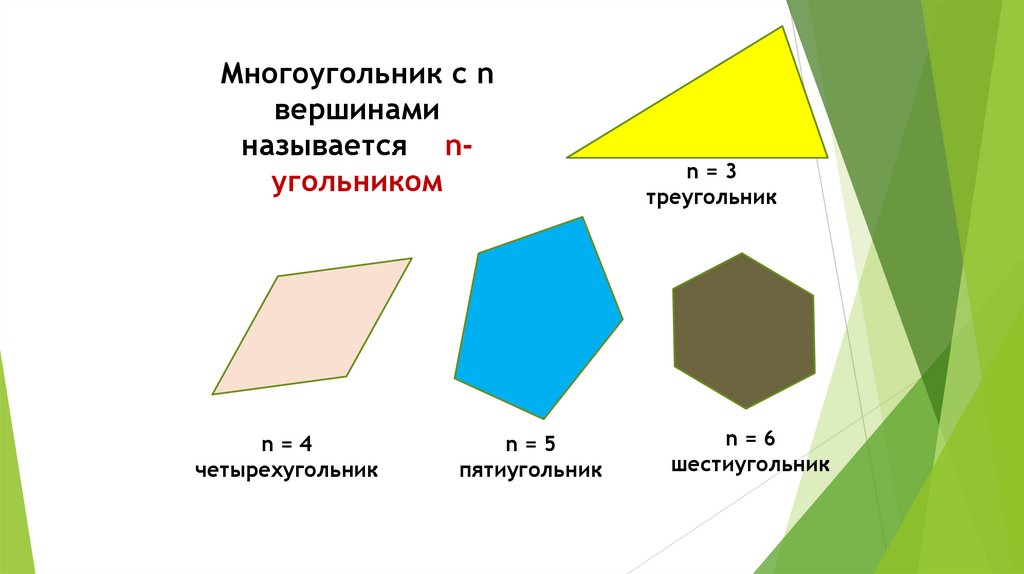
Многоугольник с nвершинами
называется nугольником
n=4
четырехугольник
n=5
пятиугольник
n=3
треугольник
n=6
шестиугольник
9.
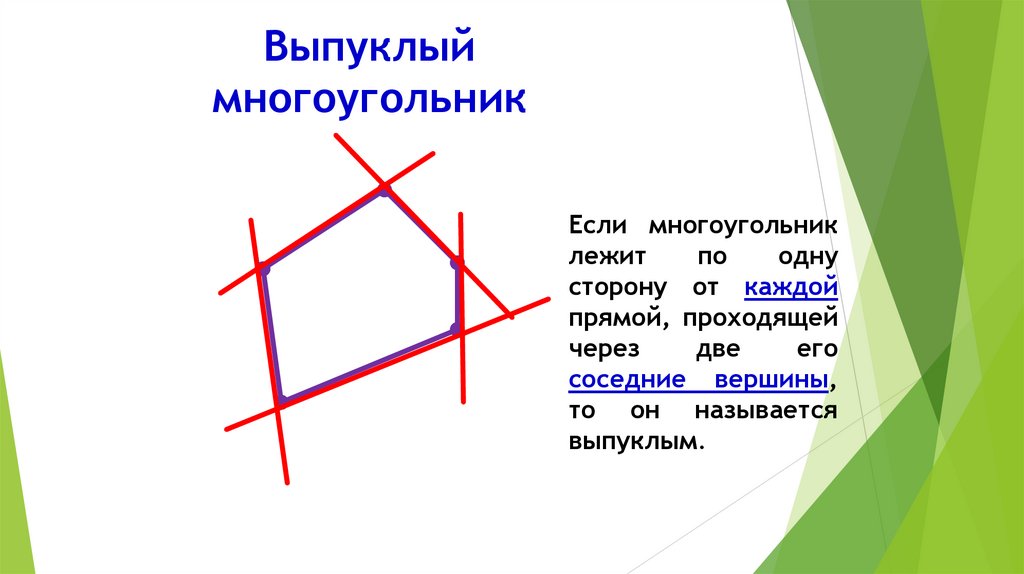
Выпуклыймногоугольник
Если многоугольник
лежит
по
одну
сторону от каждой
прямой, проходящей
через
две
его
соседние вершины,
то он называется
выпуклым.
10.
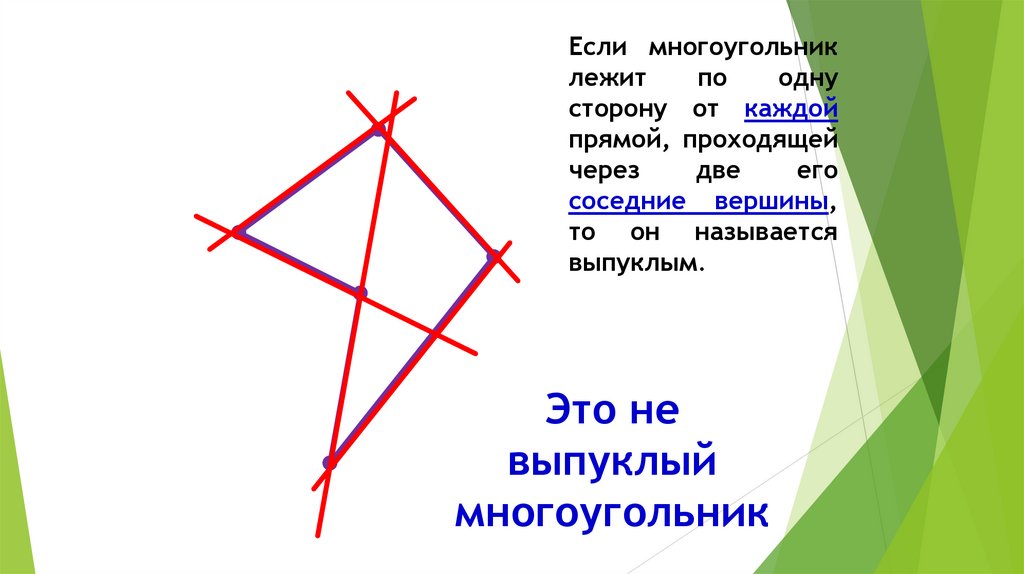
Если многоугольниклежит
по
одну
сторону от каждой
прямой, проходящей
через
две
его
соседние вершины,
то он называется
выпуклым.
Это не
выпуклый
многоугольник
11.
а)д)
б)
е)
г)
в)
е)
з)
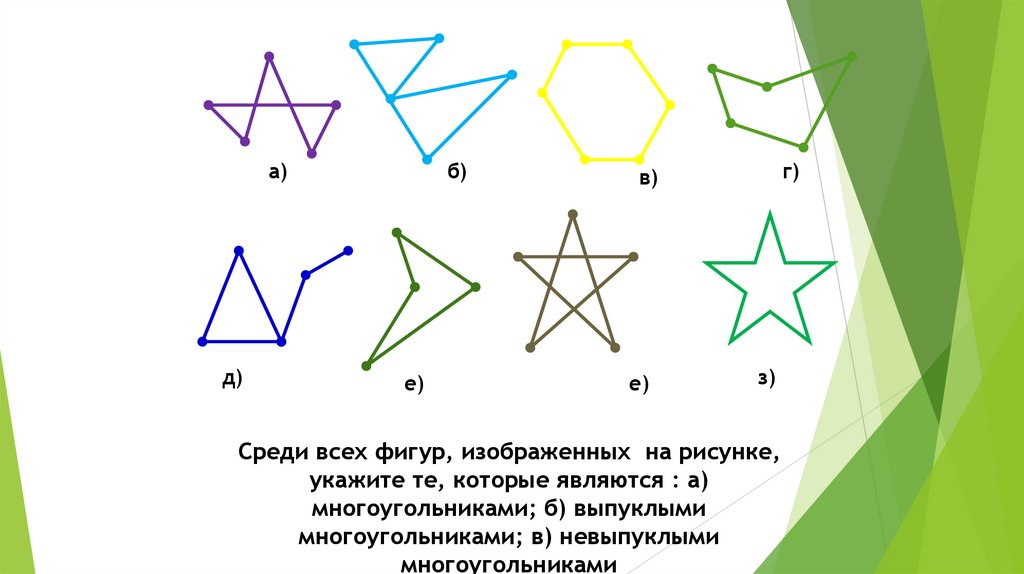
Среди всех фигур, изображенных на рисунке,
укажите те, которые являются : а)
многоугольниками; б) выпуклыми
многоугольниками; в) невыпуклыми
многоугольниками
12.
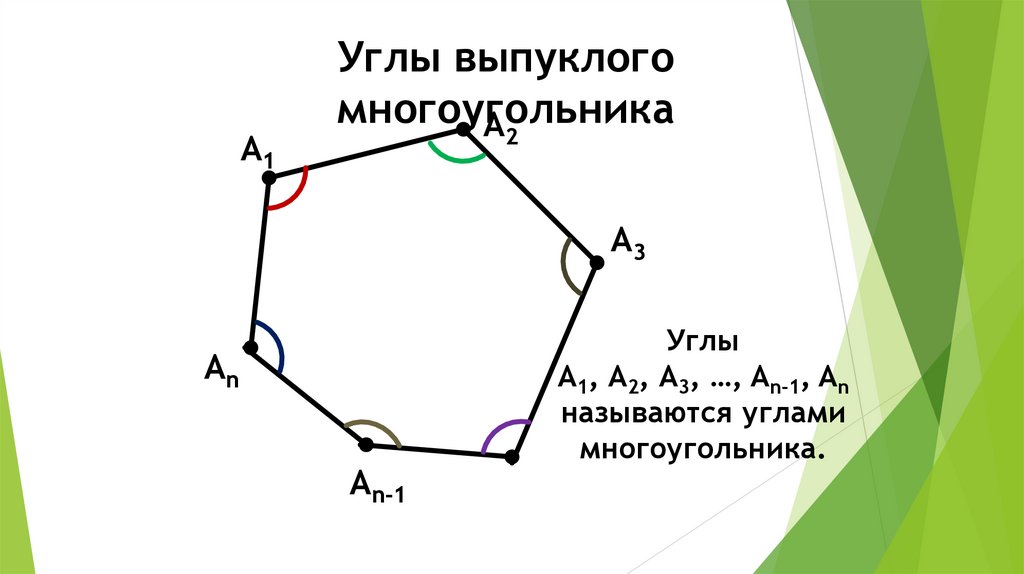
А1Углы выпуклого
многоугольника
А
2
А3
Аn
Аn-1
Углы
А1, А2, А3, …, An-1, An
называются углами
многоугольника.
13.
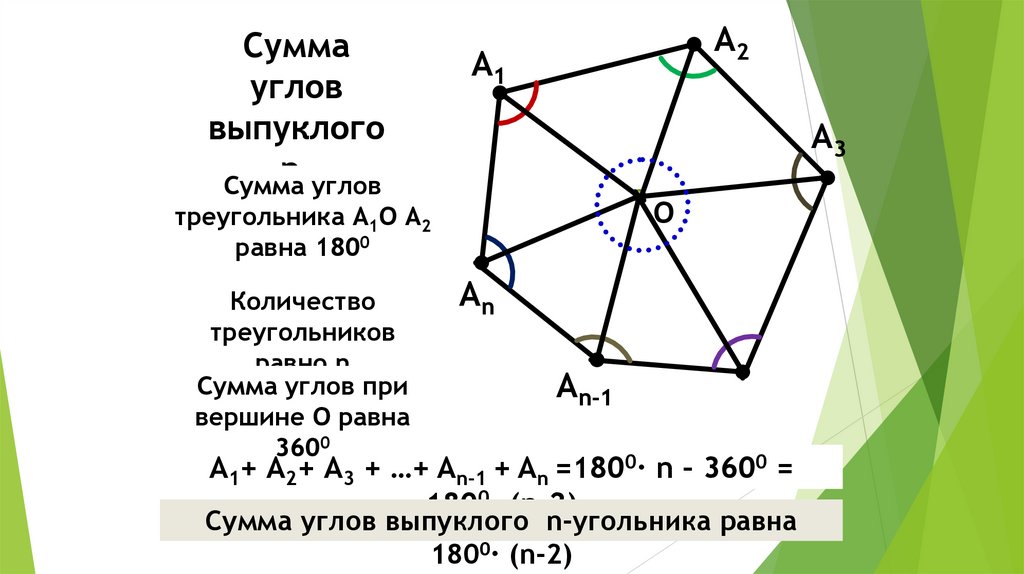
Суммауглов
выпуклого
nСумма углов
угольника
треугольника
А1О А2
А2
А1
А3
О
равна 1800
Количество
треугольников
равно n
Сумма углов при
вершине О равна
3600
Аn
Аn-1
А1+ А2+ А3 + …+ An-1 + An =1800∙ n – 3600 =
1800∙ (n-2)
Сумма углов выпуклого n-угольника равна
1800∙ (n-2)


 Математика
Математика








