Введение в компьютерную фотонику и квантовую физику

1.

Введение в
компьютерную фотонику
и квантовую физику
Алексей Дмитриевич Кондорский
1

2.

Введение
Не пугаться численных расчетов. В Сети
есть огромный набор программного
обеспечения, в том числе выпущенного под
«свободными» лицензиями.
• Для широкого круга. Научиться использовать существующие
программы
и
библиотеки.
Не
нужно
быть
асом
программирования. Обычно, достаточно иметь навыки
использования простых языков программирования (типа Python).
• Для энтузиастов. Развитие методов нового поколения для:
o моделирования сложных квантовых систем (Монте-Карло);
o разработки методов управления квантовыми системами
(оптимальное управление, генетические алгоритмы);
o анализа и обработки данных расчетов (нейронные сети);
o …
2

3.

Цели и задачи курса
• Что можно посчитать, а что нельзя?
• Не пытаться решать аналитически задачи, которые проще
засунуть в компьютер и решить стандартными программами.
• Какой численный подход выбрать? Общее представление
какие методы для чего эффективны. К каким пакетам
программ нужно присмотреться для решения тех или иных
задач.
• Рассмотреть
примеры
использования
существующих
открытых кодов и понять как комбинировать методы и
программы для получения нужного результата.
Научиться правильно ставить физическую
задачу и подбирать подходящую модель.
3

4.

Особенности современной компьютерной
физики
• Мыслить не функциями, а операторами.
Оператор эволюции. Матричная экспонента. Преобразование
Фурье…
Элементарные функции, спец. функции, операторы…
• Выбирать представления.
Координатное или импульсное. Распространение волновой
функции vs. интегрирование по траекториям и т.п.
• Быть готовыми к тому, что вы можете не понять как
компьютер получил результат.
Оптимальное управление, генетические алгоритмы,
нейронные сети и т.п.
• Важность качественного понимания результата и физики
моделируемых процессов.
4

5.

Основные задачи компьютерной фотоники
• Расчёт спектральных и оптических свойств (квантовые системы и
метаматериалы)
• Задача рассеяния (квантовые системы и наноструктуры)
• Расчёт добротности и скоростей затухания сигнала в различных
устройствах (субволновые оптические устройства)
Особенности задач нанофотоники и нанооптики
Электродинамика
Квантовая механика
• Радиофизика, но с возможностью
материала поглощать и излучать.
• Квантоворазмерный эффект.
Ограничение размеров
волновой функции влияет на
спектр.
• Влияние размеров на диэлектрическую функцию, нарушение
применимости электродинамики
сплошных сред.
• Ближние электромагнитные
поля. Недипольные
взаимодействия
Численное интегрирование волновых уравнений
Максвелла и Шредингера.
5

6.

Уравнения Максвелла в отсутствие
зарядов и токов
B( x, y , z, t )
c E ( x, y , z, t ),
t
D ( x, y , z, t )
c H ( x, y , z, t ),
t
B( x, y , z, t ) ( x, y , z ) E ( x, y , z, t ),
D ( x, y , z, t ) ( x, y , z ) H ( x, y , z, t ).
Шесть действительных функций —
зависимостей векторов напряженностей
электро-магнитных полей от координат
и времени. Число координат – всего 3.
( x, y , z, t ) ˆ
A( x, y , z ) ( x, y , z, t ),
t
E X ( x, y , z, t )
E ( x, y , z, t )
Y
E ( x, y , z, t )
( x, y , z, t ) Z
.
H X ( x, y , z , t )
H Y ( x, y , z, t )
H
(
x
,
y
,
z
,
t
)
Z
Электрическое и магнитное поле плоской волны
6

7.

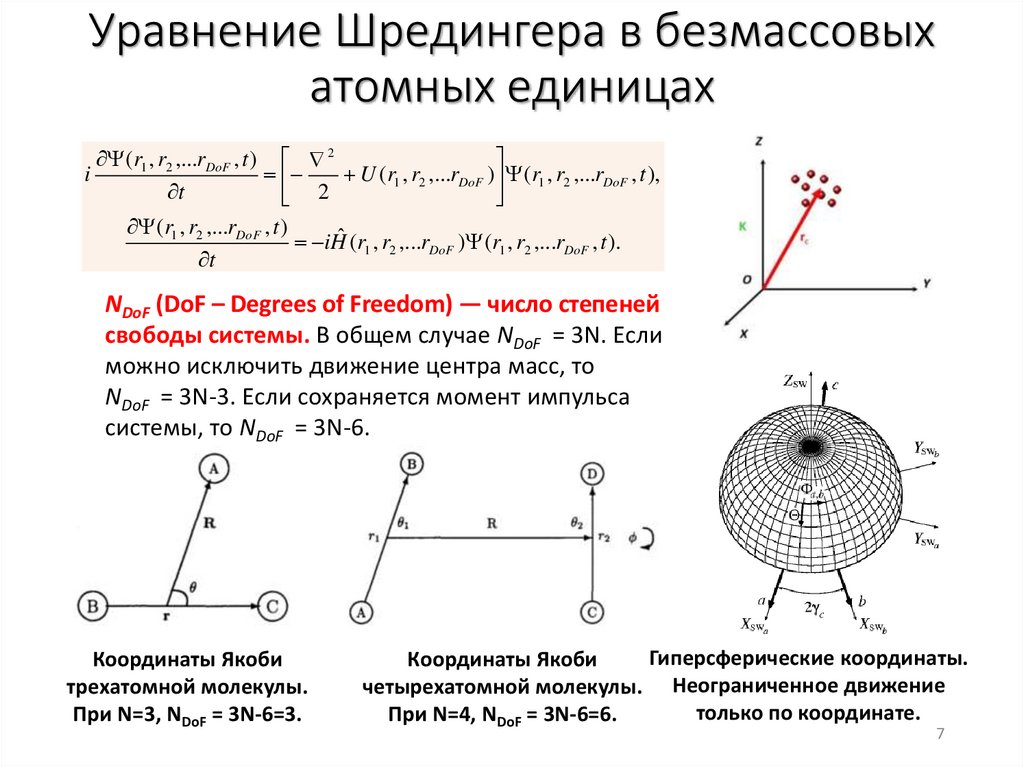
Уравнение Шредингера в безмассовых
атомных единицах
(r1 , r2 ,...rDoF , t ) 2
i
U (r1 , r2 ,...rDoF ) (r1 , r2 ,...rDoF , t ),
t
2
(r1 , r2 ,...rDoF , t )
iHˆ (r1 , r2 ,...rDoF ) (r1 , r2 ,...rDoF , t ).
t
NDoF (DoF – Degrees of Freedom) — число степеней
свободы системы. В общем случае NDoF = 3N. Если
можно исключить движение центра масс, то
NDoF = 3N-3. Если сохраняется момент импульса
системы, то NDoF = 3N-6.
Координаты Якоби
трехатомной молекулы.
При N=3, NDoF = 3N-6=3.
Гиперсферические координаты.
Координаты Якоби
четырехатомной молекулы. Неограниченное движение
только по координате.
При N=4, NDoF = 3N-6=6.
7

8.

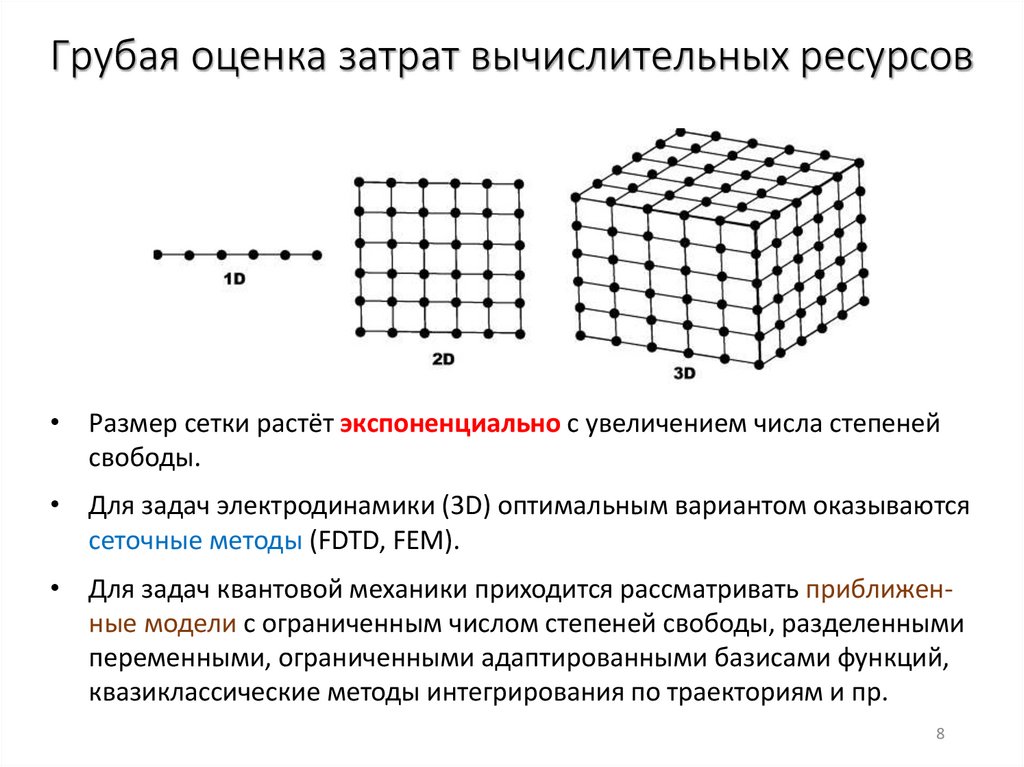
Грубая оценка затрат вычислительных ресурсов
• Размер сетки растёт экспоненциально с увеличением числа степеней
свободы.
• Для задач электродинамики (3D) оптимальным вариантом оказываются
сеточные методы (FDTD, FEM).
• Для задач квантовой механики приходится рассматривать приближенные модели с ограниченным числом степеней свободы, разделенными
переменными, ограниченными адаптированными базисами функций,
квазиклассические методы интегрирования по траекториям и пр.
8

9.

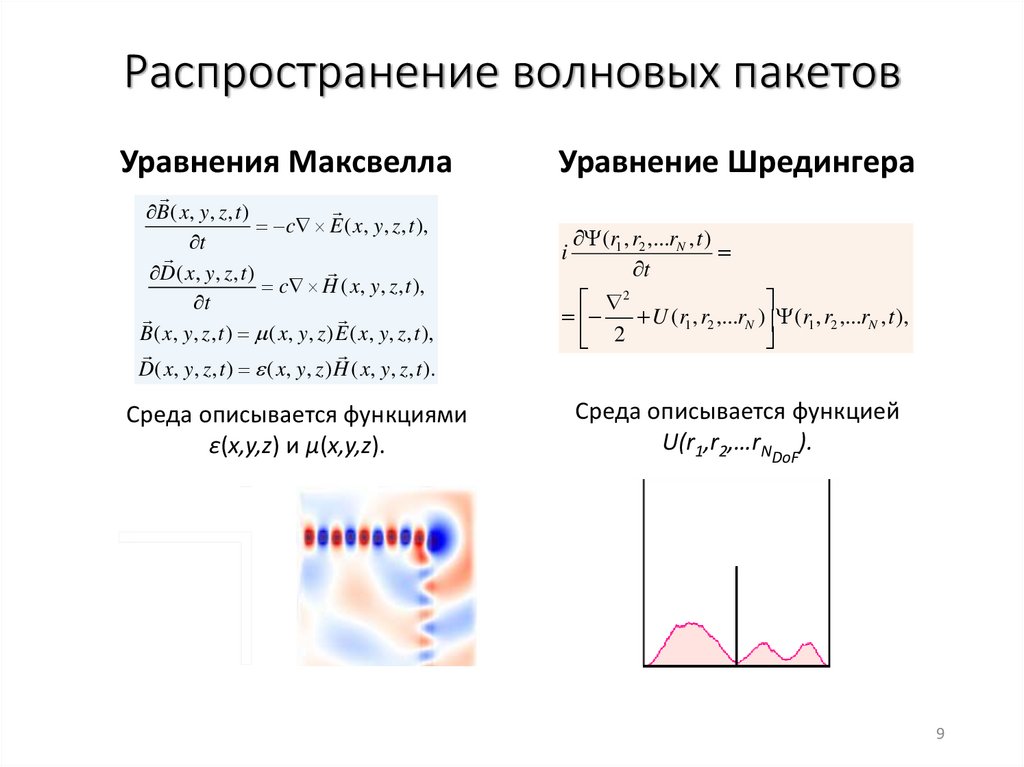
Распространение волновых пакетов
Уравнения Максвелла
B( x, y , z, t )
c E ( x, y , z, t ),
t
D ( x, y , z, t )
c H ( x, y , z, t ),
t
B( x, y , z, t ) ( x, y , z ) E ( x, y , z, t ),
D ( x, y , z, t ) ( x, y , z ) H ( x, y , z, t ).
Среда описывается функциями
ε(x,y,z) и μ(x,y,z).
Уравнение Шредингера
(r1 , r2 ,...rN , t )
t
2
U (r1 , r2 ,...rN ) (r1 , r2 ,...rN , t ),
2
i
Среда описывается функцией
U(r1,r2,…rNDoF).
9

10.

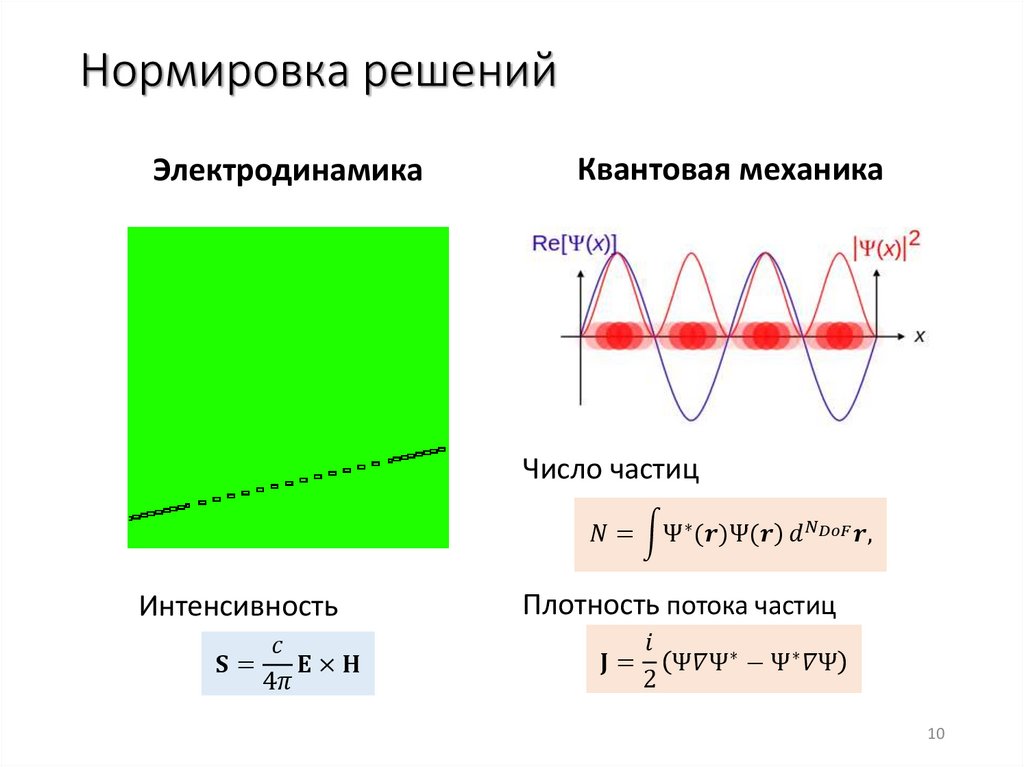
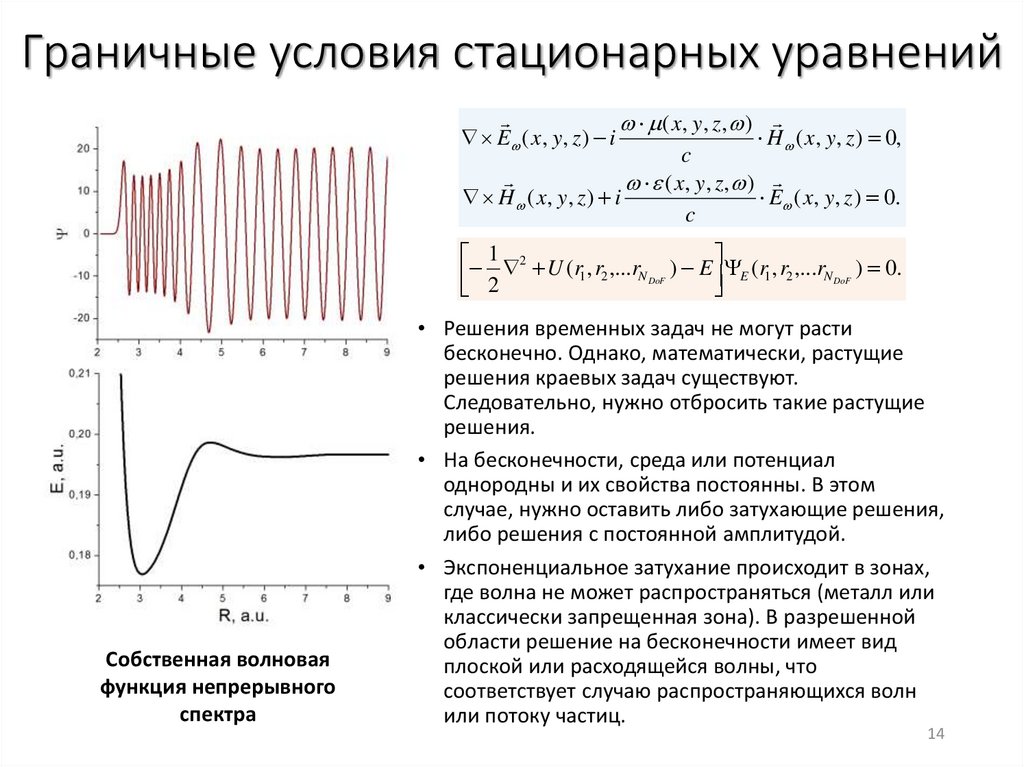
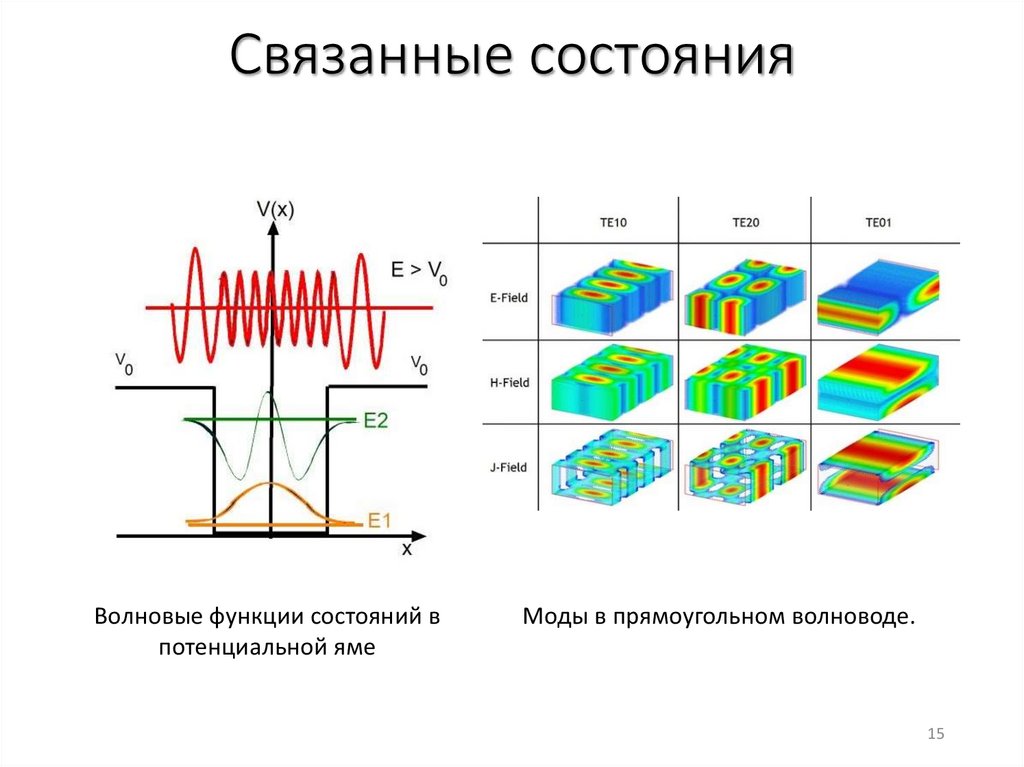
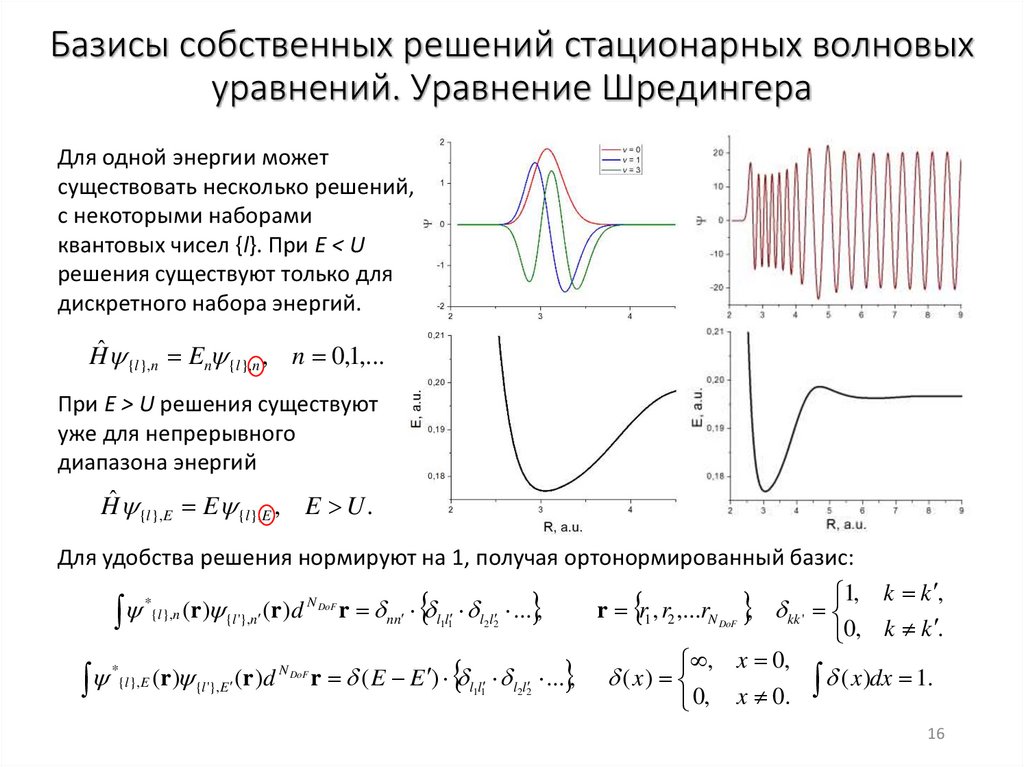
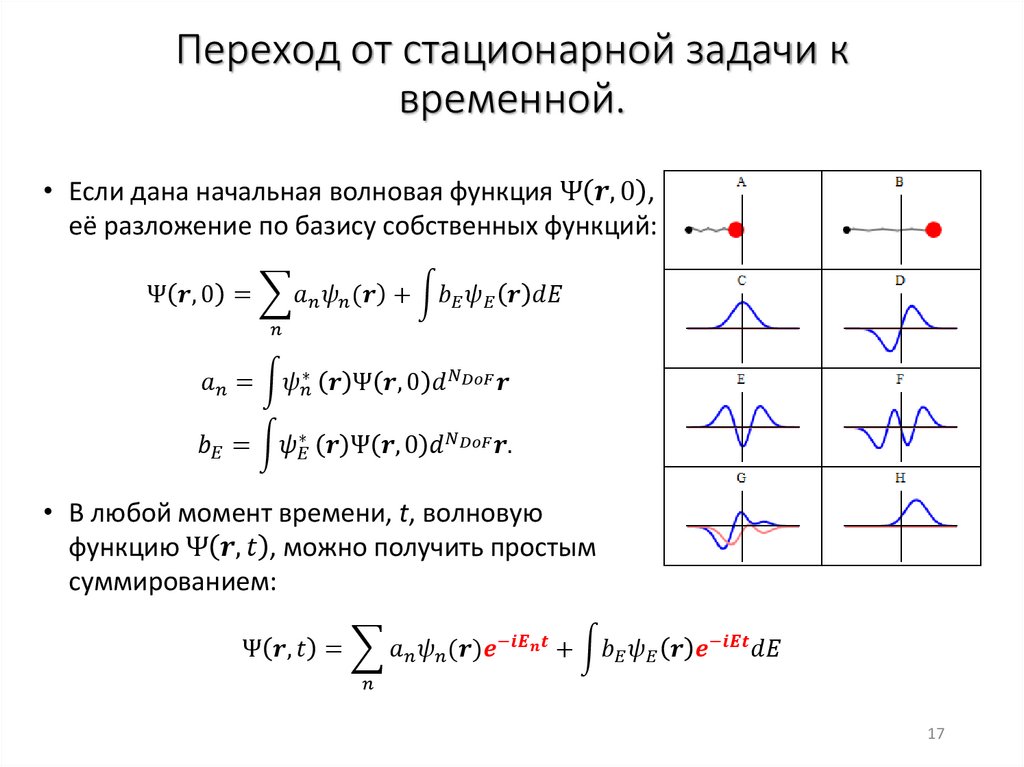
Нормировка решений
Электродинамика
Квантовая механика
Число частиц