Электромагнетизм и квантовая механика

1. Тема: Электромагнетизм и квантовая механика

Электромагнитное поле
Электромагнитные волны
Элементы квантовой механики

2.

Поток вектора напряженности электростатического поля.
dΦ ( E n )dS
1
Φ
dΦ
(
E
dr
)
Φ
E
0qi
L
0S
i
1
( E n )dS
S
r2
Aq
F
Uq
( dr ) ( Edr ) ( (r1 ) (r2 ))
q r1 q
r1
r2
dV
0 V

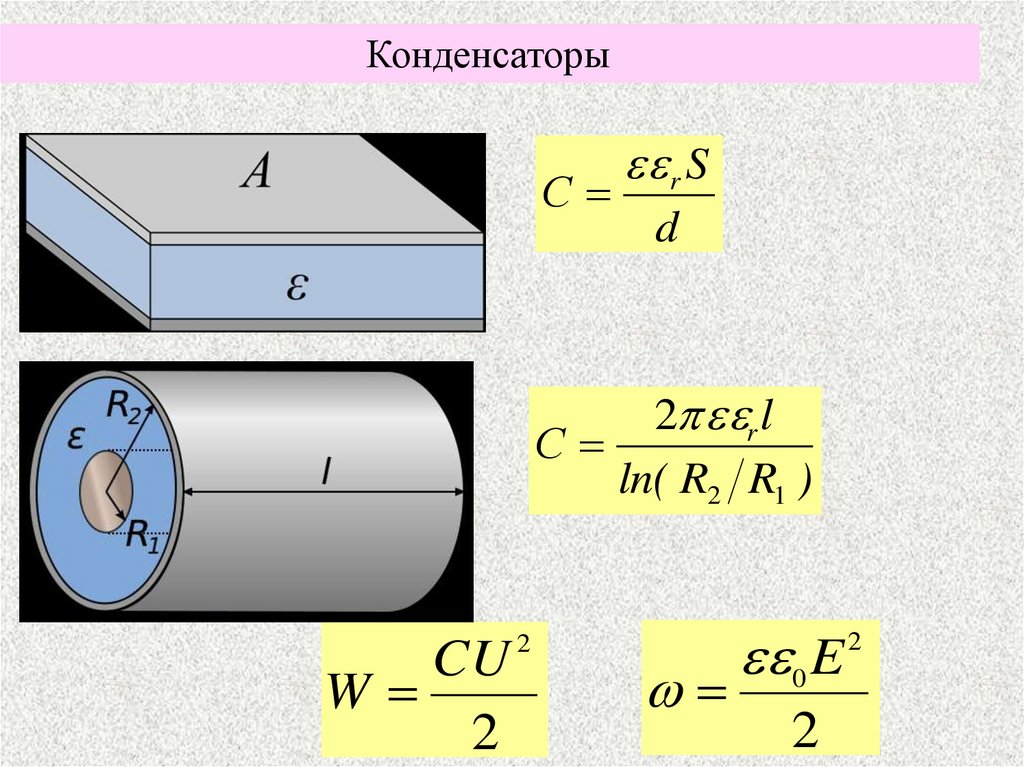
3.

Конденсаторы
С
r S
d
2 r l
С
ln( R2 R1 )
CU
W
2
2
0 E
2
2

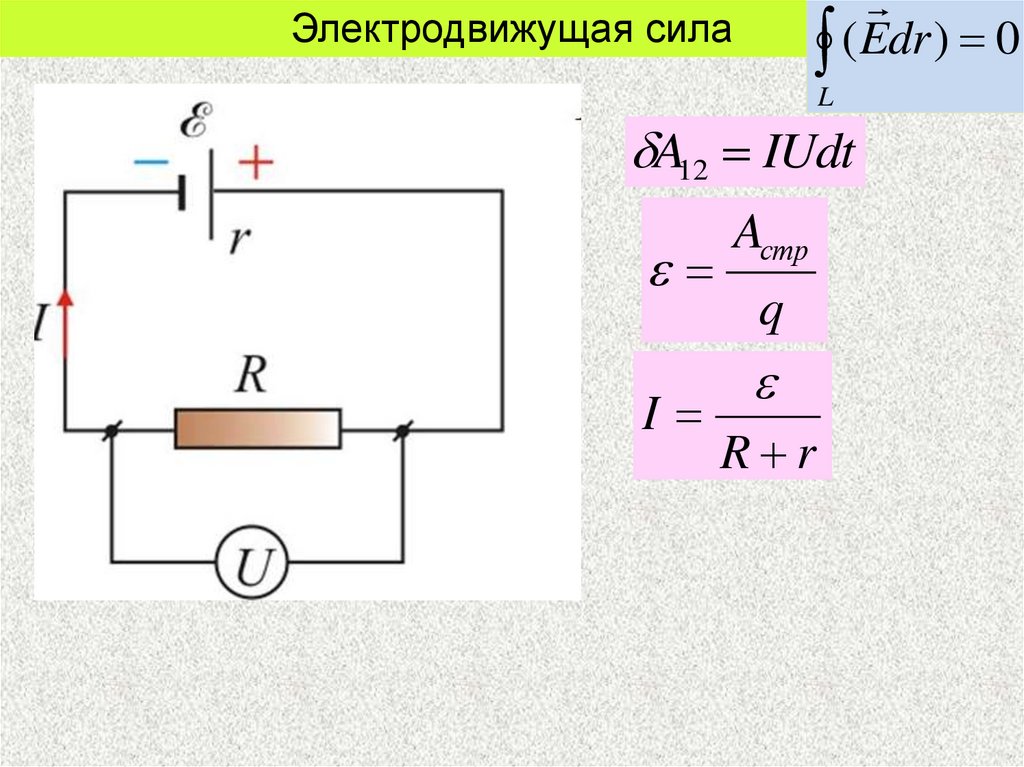
4.

Электродвижущая сила
( Edr ) 0
L
A12 IUdt
Aстр
q
I
R r

5.

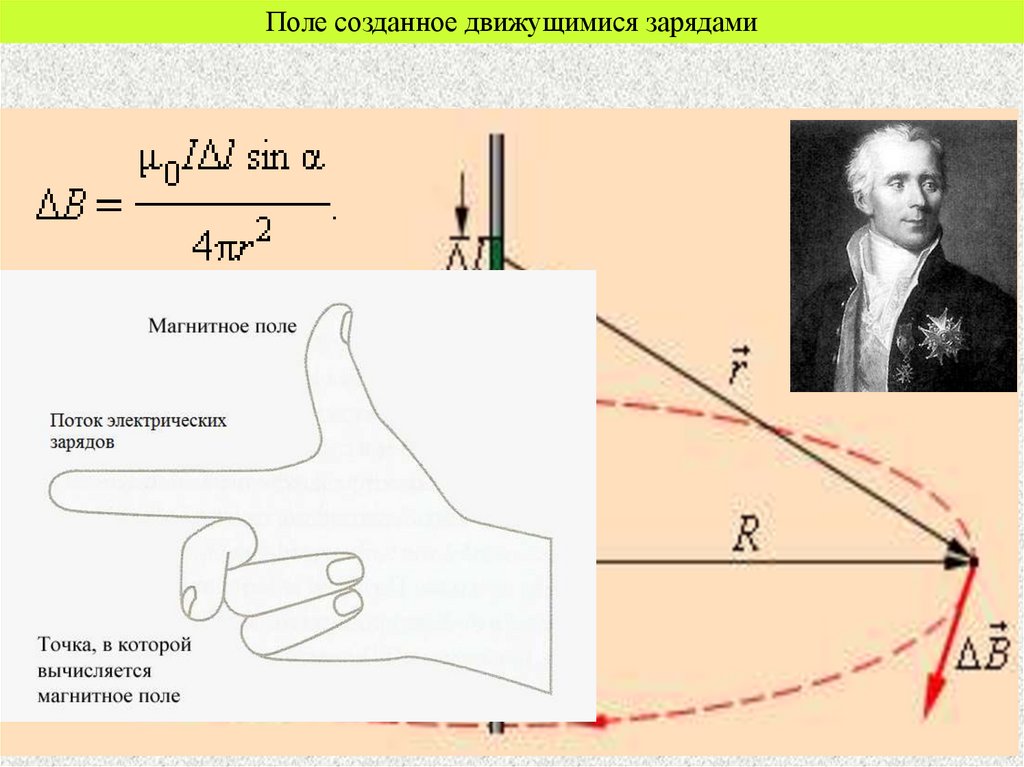
Поле созданное движущимися зарядами

6.

Соленоид
B
B
0 I
2R

7.

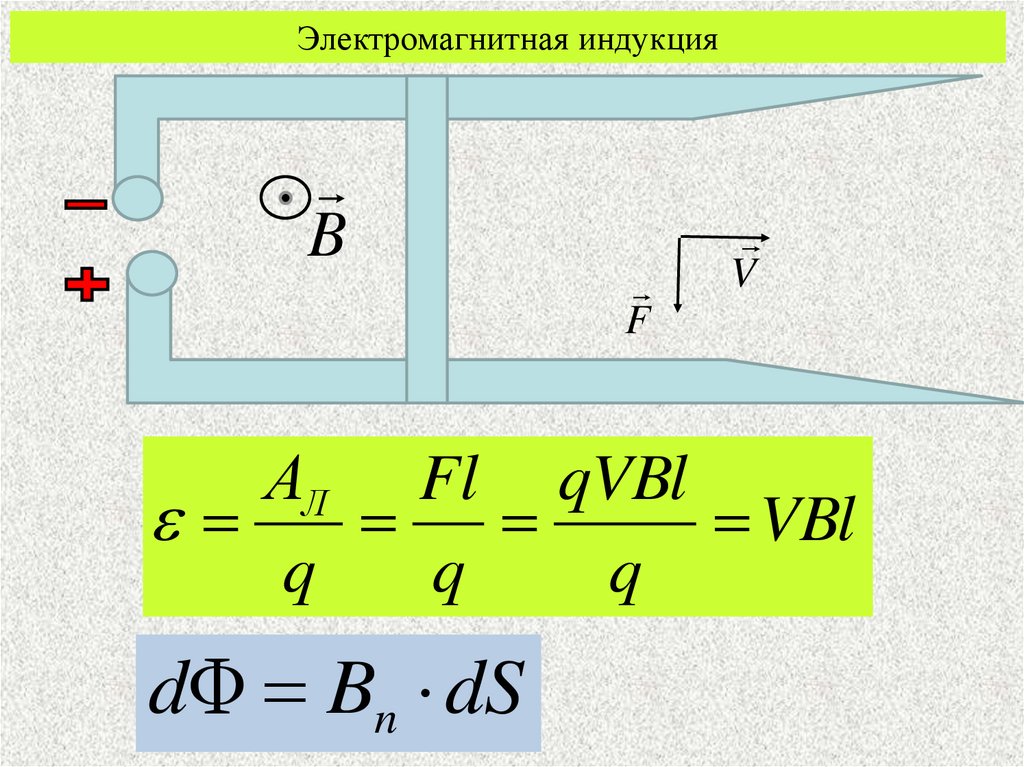
Сила Лоренца.

8.

Электромагнитная индукция
B
F
V
АЛ Fl qVBl
VBl
q
q
q
dΦ Bn dS

9.

Магнитный поток и циркуляция магнитного поля.
(B
n
( E dl ) 0
dS ) 0
S
L
N
( B dl ) 0 I
L
i 1
Φ
i
t

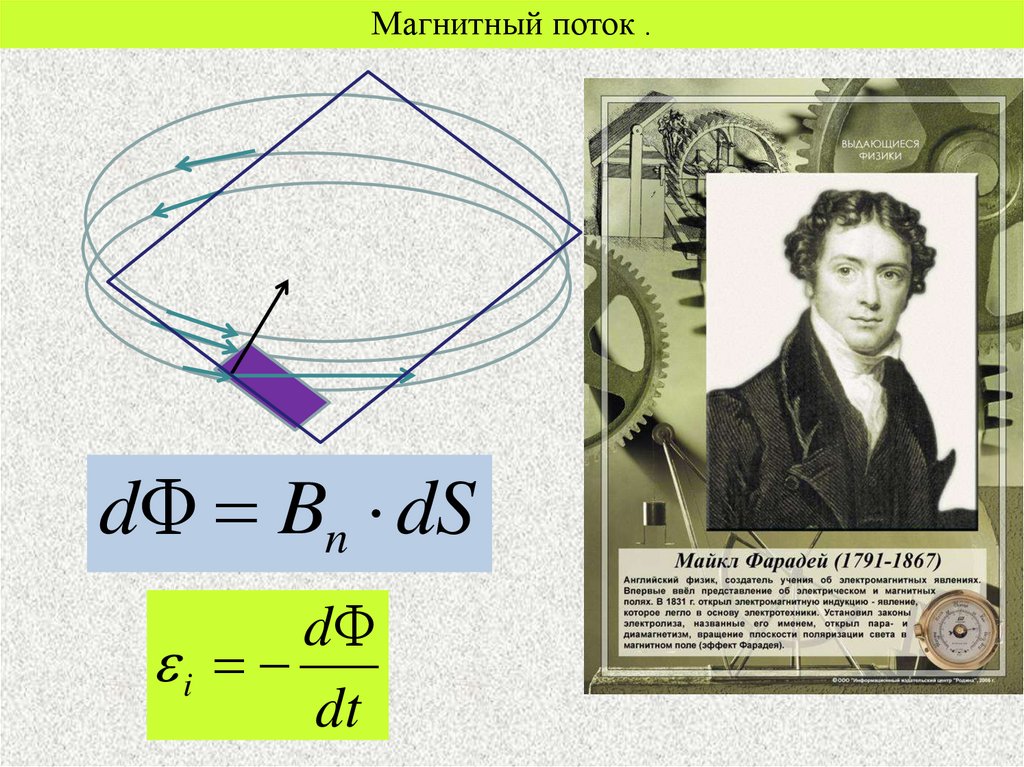
10.

Магнитный поток .
dΦ Bn dS
dΦ
i
dt

11.

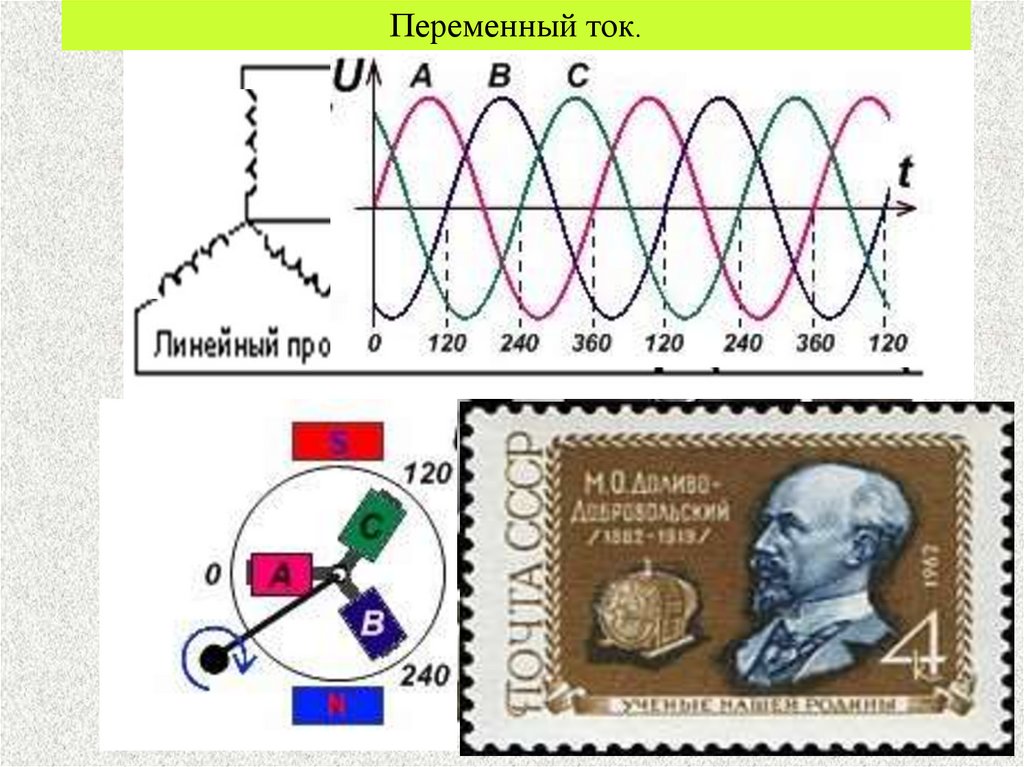
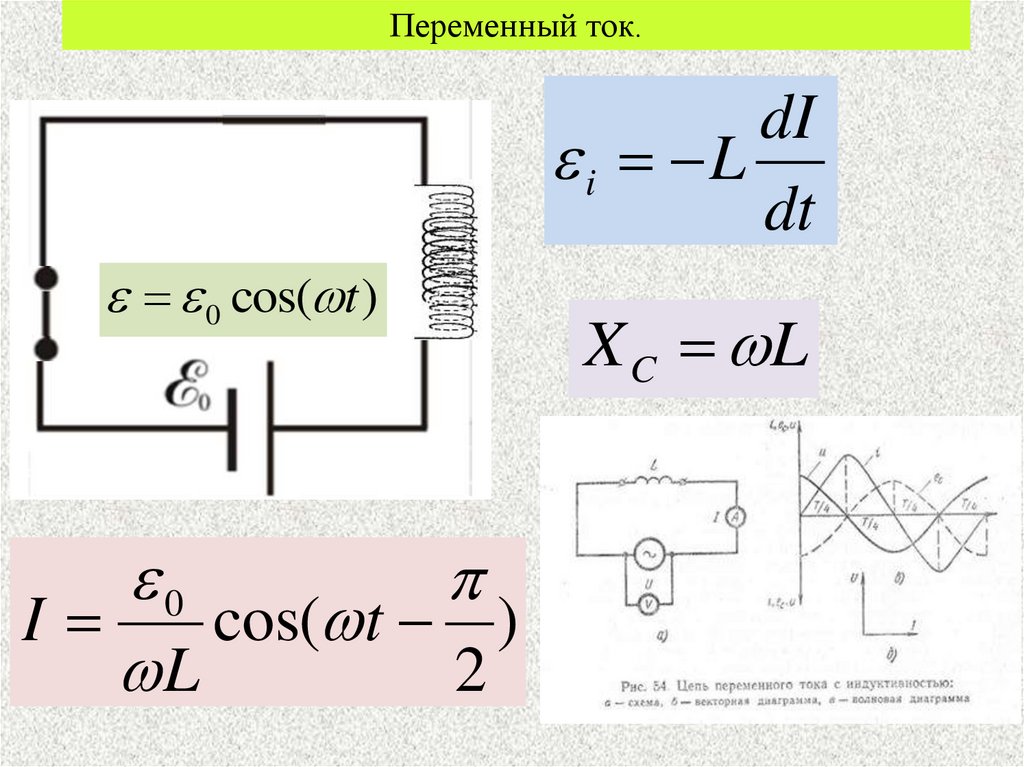
Переменный ток.

12.

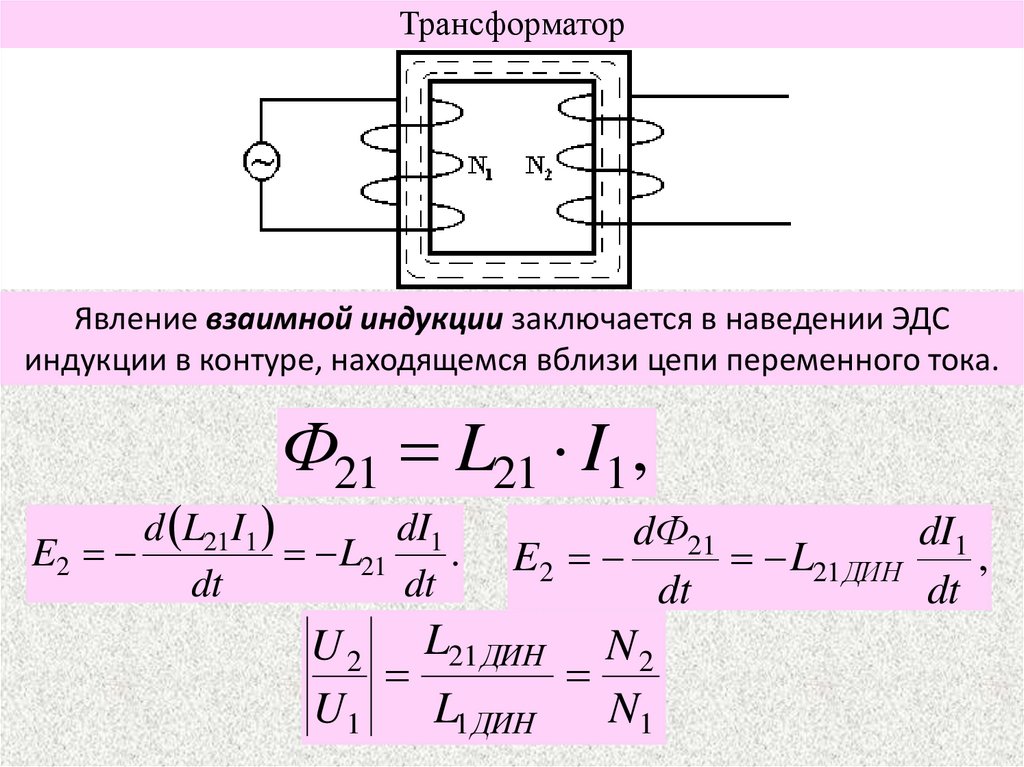
Трансформатор
Явление взаимной индукции заключается в наведении ЭДС
индукции в контуре, находящемся вблизи цепи переменного тока.
Ф21 L21 I1,
d L21I1
dI1
E2
L21
.
dt
dt
dФ21
dI1
E2
L21 ДИН
,
dt
dt
U 2 L21 ДИН N 2
U1
L1 ДИН
N1

13.

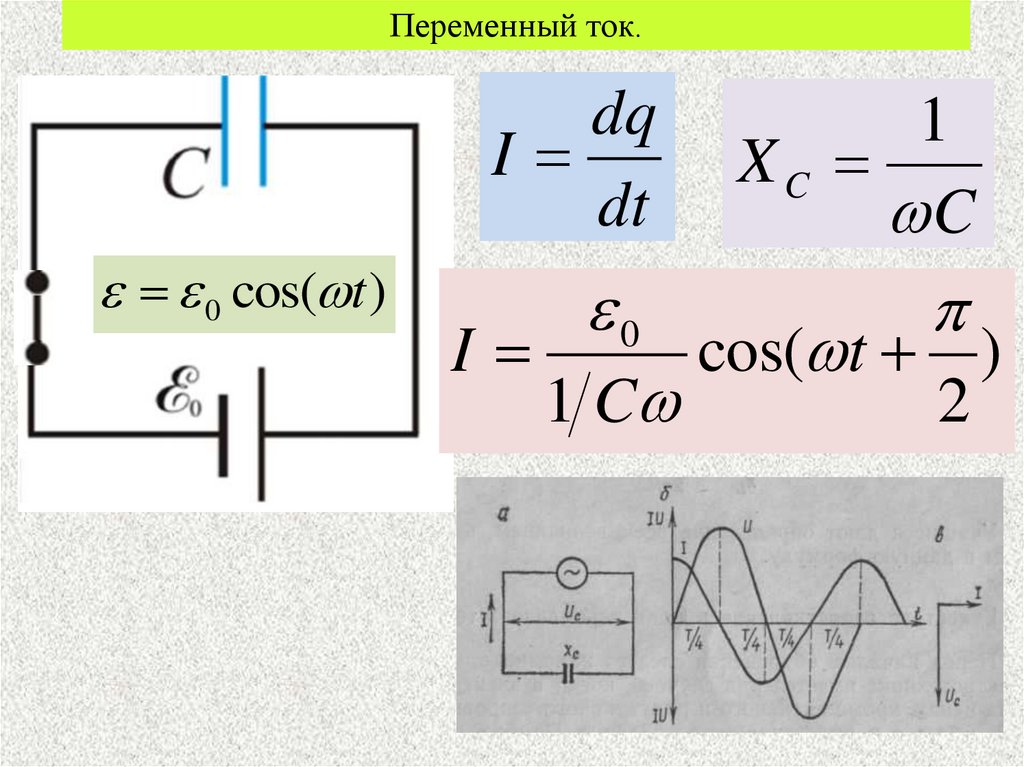
Переменный ток.
dq
I
dt
0 cos( t )
1
XC
C
0
I
cos( t )
1 C
2

14.

Переменный ток.
dI
i L
dt
0 cos( t )
0
I
cos( t )
L
2
X C L

15.

Переменный ток.
рез
0 cos( t )
I
0
R 2 ( L 1 C ) 2
cos( t )
1
LC
o

16.

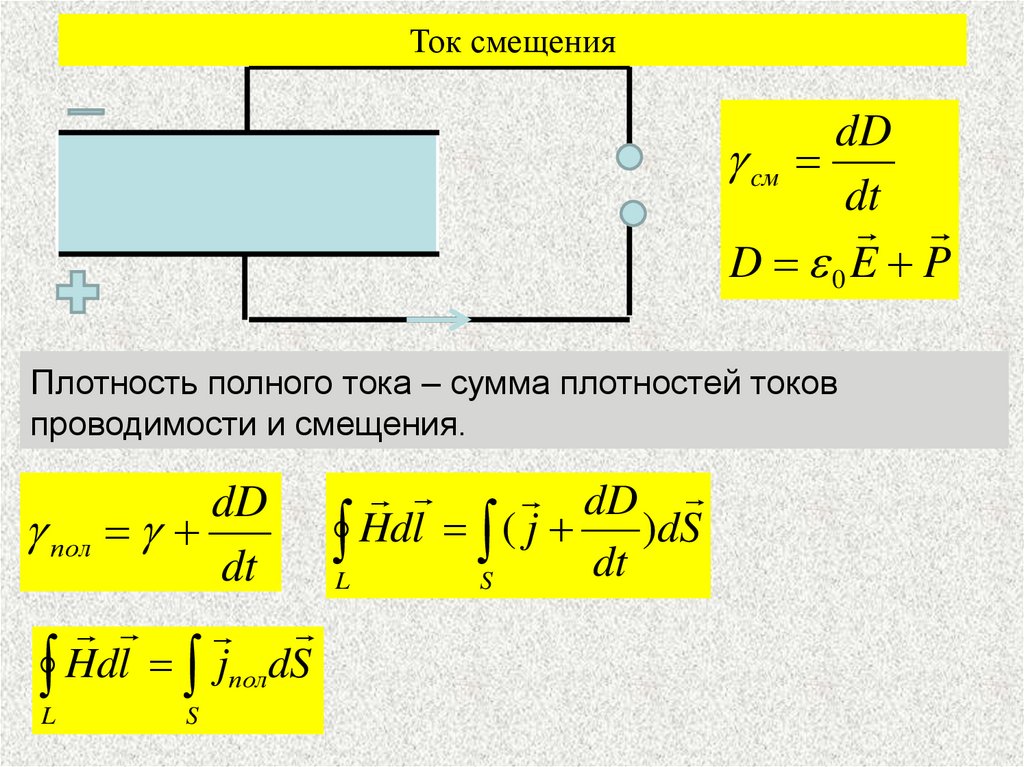
Ток смещения
dD
cм
dt
D 0E P
Ток
смещения
– этотока
скорость
изменения
электрического
Плотность
полного
– сумма
плотностей
токов
смещения
.
проводимости
и смещения.
пол
dD
dt
Hdl jполdS
L
S
dD
L Hdl S ( j dt )dS

17.

B
L Edl S t dS
DdS dV
S
V
D 0 E
B 0 H
Edl
lim
ΔS 0
L
B
ΔS
t
Уравнения Максвелла.
D
L Hdl S ( j t )dS
( BdS ) 0
S
Я глубоко убежден в
реальности
электромагнитных
волн!
DdS
lim
ΔV 0
S
ΔV
E
2
E 0 0
t

18.

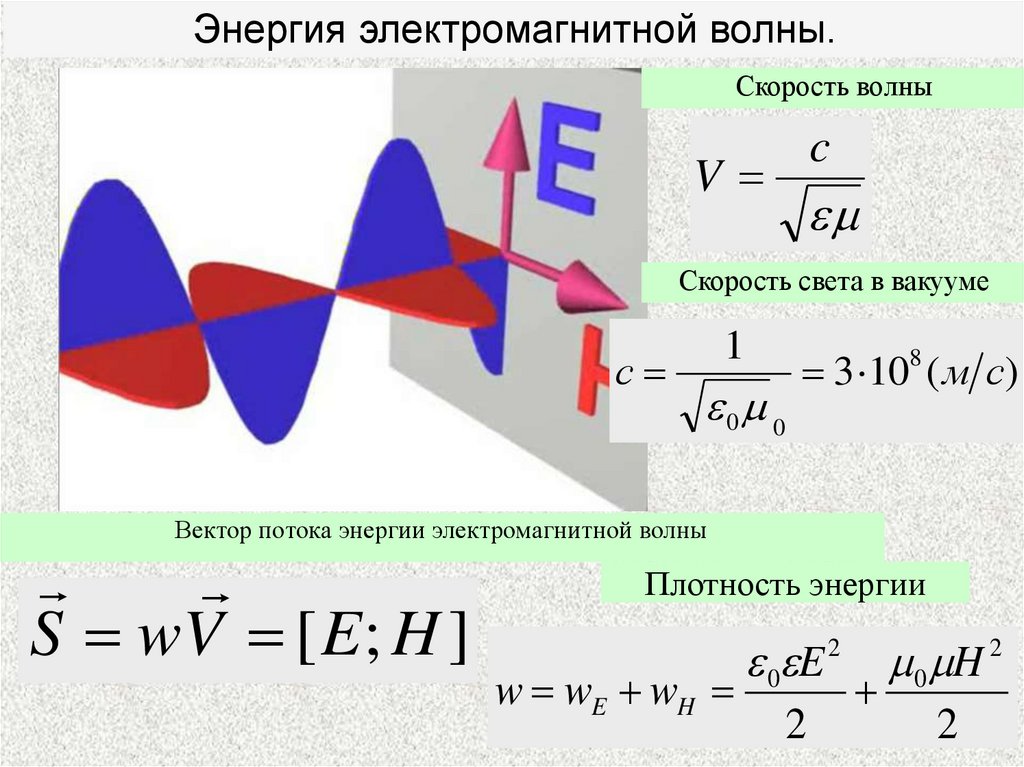
Энергия электромагнитной волны.
Скорость волны
V
c
Скорость света в вакууме
с
1
0 0
3 108 ( м с)
Вектор потока энергии электромагнитной волны
S wV [ E ; H ]
Плотность энергии
0 E 2 0 H 2
w wE wH
2
2

19.

Тепловое
излучение
– это электромагнитное
излучение
Тело,
способное
поглощать
при
любой
температуре
все в
Спектральный
коэффициент
поглощения
характеризуется
отношеИспускательная
способность
–это
количество
энергии,широкого
испускаемой
спектрального
обусловленное
тепловыми
колебаниями
падающее
насостава,
него
излучение
всех
частот,
называется
нием
потока
излучения
поглощенного
телом
к потоку
падающего
на тело
единицу
времени
единицей
поверхности
тела
в единичном
интервале
электрических
зарядов
(электронов,
входящих вW(T;λ);
состав λ(T)
вещества.
излучения.
частот.
абсолютно
черным
телом. ионов),
Характеристики:
Тепловое излучение находится в термодинамическом равновесии с
Энергетическая
Спектральная плотность
светимость –энергии
энергияизлучения
испускаемая
– это
в единицу
энергия излучения
времени в
излучателем. Количество излучаемой энергии стремится сравняться с
единицей
единице объема,
поверхности
приходящаяся
излучающего
на единичный
тела по всем
интервал
направлениям
частот u(ω,Т).
R(T).
количеством поглощаемой.
R( T ) T
4

20.

Функция Кирхгофа- отношение испускательной и
поглощательной способности тела не зависит от природы
тела и является функцией частоты и температуры.
Спектр излучения абсолютно черного тела является сплошным.
Распределение излучения зависит
от длины волны (частоты). При
некотором значении длины волны
достигает максимума.
С повышением температуры максимум
излучения смещается в сторону более
коротких длин волн.
T const
h

21.

Дифракция электронов на круглом
отверстии
Дифракция света (красный) на круглом
отверстии
i
(t , r ) A0 exp( t ) (r )
Английский ученый бельгийского происхождения Дирак предложил описывать
состояние элементарных частиц как кванты излучения с помощью волновой
функции

22.

Волновое уравнение Шредингера (общий случай).
Волновая функция
i
(t , r ) exp( t ) (r )
Система
Потенциал
Свободная
частица,
движущаяс
я вдоль
r
U (r ) 0
Волновое Уравнение
2 2
(r ) U (r ) (r ) (r )
2m
Уравнение Шредингера
Волновая функция
2 2
(r ) (r )
2m
(r ) A exp( ik r ) B exp( ik r )
Связь энергии с
волновым
вектором.
2k 2
2m
p 2
k

23.

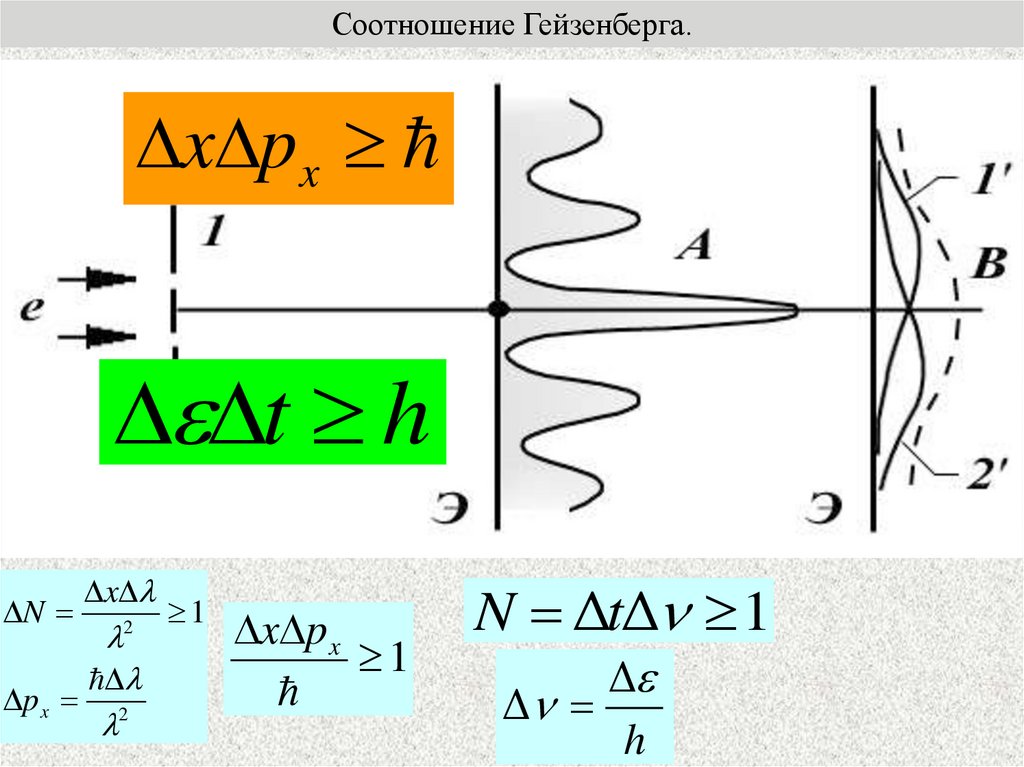
Соотношение Гейзенберга.
x px
t h
N
p x
x
2
2
1
x p x
1
N ΔtΔ 1
Δ
Δ
h

24.

Элементарные квантовые системы ().
i
(t , r ) exp( t ) (r )
2 2
(r ) U (r ) (r ) (r )
2m
Система
Атом
водорода
Потенциал
Zqe2
U ( x) k
r
Волновая функция
Связь
энергии с
волновым
вектором.
2m
n 2i
2 (r ) 2 e (U (r ) ) (r ) 0
n
1 (r )
1
a3
exp( r a)
Ll l (l 1)
l 0,1,...,(n 1)
Llz ml
l 0, 1, 2..., l

25.

Ui
Wn 2
n
Ll l (l 1)
l 0,1,...,(n 1)
Ll ml
z
ml 0, 1, 2..., l
Ls ms
z
ms 1 2