Похожие презентации:
Расстояния в пространстве
1.
Расстояния впространстве
2.
Расстояние между точками А и Вможно вычислить:
1) как длину отрезка АВ, если отрезок
АВ удается включить в некоторый
треугольник в качестве одной из его
сторон;
2) по формуле нахождения расстояния
между точками ;
3) по формуле нахождения длины
вектора.
3.
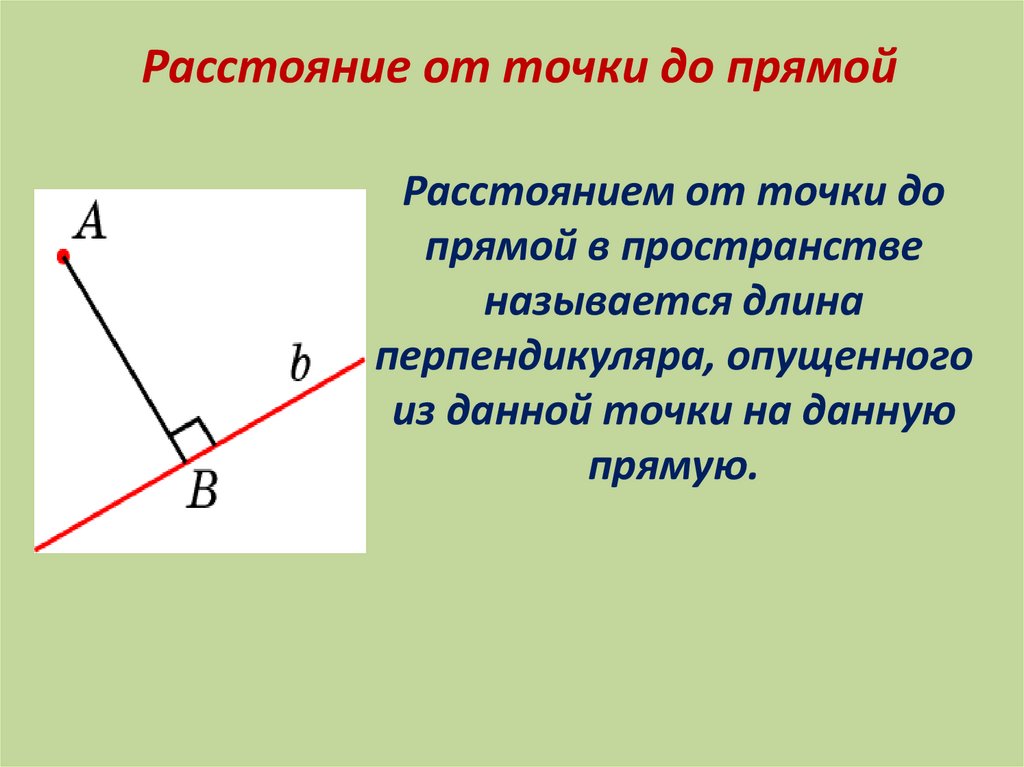
Расстояние от точки до прямойРасстоянием от точки до
прямой в пространстве
называется длина
перпендикуляра, опущенного
из данной точки на данную
прямую.
4.
• Расстояние от точки до прямой можновычислить:
1) как длину отрезка перпендикуляра, если
удается включить этот отрезок в
некоторый треугольник в качестве
одной из высот;
2) используя векторный метод;
3) используя координатно-векторный
метод.
5.
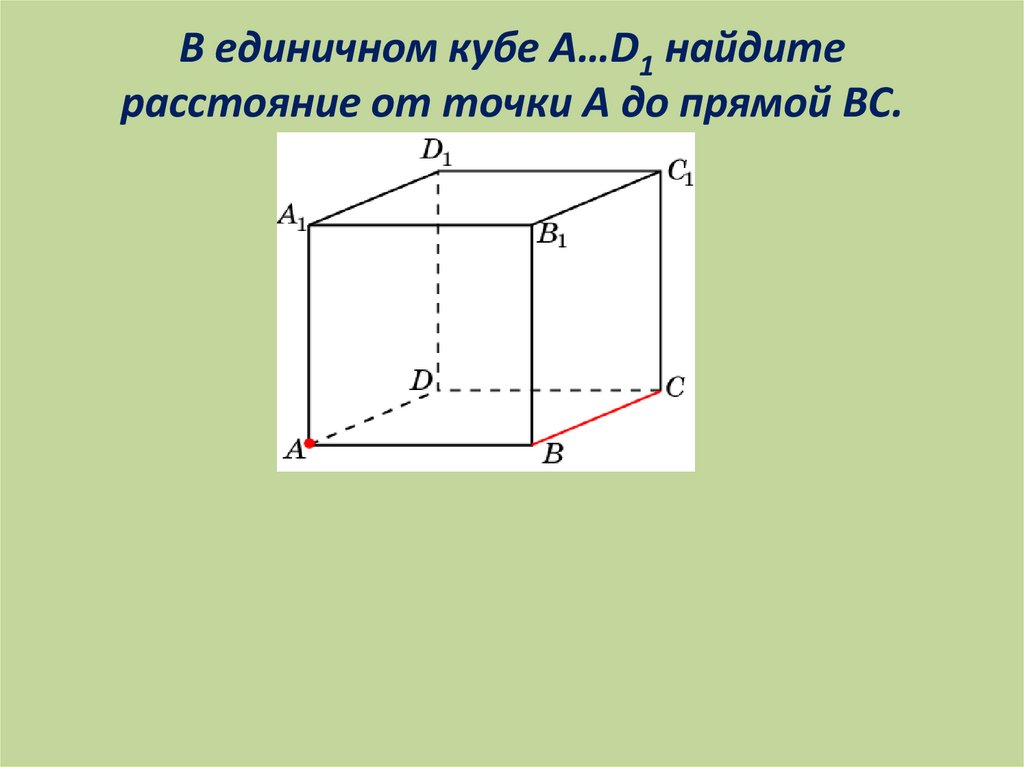
В единичном кубе A…D1 найдитерасстояние от точки A до прямой BC.
6.
В единичном кубе A…D1 найдитерасстояние от точки A до прямой CB1.
7.
Задачи для самостоятельного решения1)В правильной треугольной призме
ABCA₁B₁C₁ , все ребра которой равны 1,
найдите расстояние от точки А до прямой
ВС ₁ .
2) В правильной шестиугольной призме
АВC DEFA₁B₁C₁D₁ E₁ F₁ A₁ , все ребра которой
равны 1, найдите расстояние от точки А до
прямой: а) DЕ;
б) D₁E₁ ; в) B₁C₁ ; г) BE₁ ; д) BC₁ ;
е) CE₁ ; ж) CF₁ ; з) CB₁ .
8.
Задание № 14 (2 балла)• 4. Дана правильная треугольной призма
ABCA1B1C1.
• а) Докажите, что плоскость α, проходящая
через прямую AB1 и центр грани ACC1A1
делит объем призмы в отношении 2 : 1.
• б) Пусть высота призмы равна 2, сторона
основания равна 1. Найдите расстояние от
точки B1 до прямой AC1.
9.
Расстояние от точки до плоскостиРасстоянием от точки
до
плоскости
в
пространстве
называется
длина
перпендикуляра,
опущенного из данной
точки
на
данную
плоскость.
10.
• Расстояние от точки до плоскости, не содержащейэту точку, есть длина отрезка перпендикуляра,
опущенного из этой точки на плоскость.
• Расстояние между прямой и параллельной ей
плоскостью равно длине их общего перпендикуляра.
• Расстояние между прямой и параллельной ей
плоскостью равно расстоянию от любой точки
этой прямой до плоскости.
• Расстояние между двумя параллельными
плоскостями равно длине их общего перпендикуляра.
• Расстояние между двумя параллельными
плоскостями равно расстоянию между точкой
одной из этих плоскостей и другой плоскостью.
11.
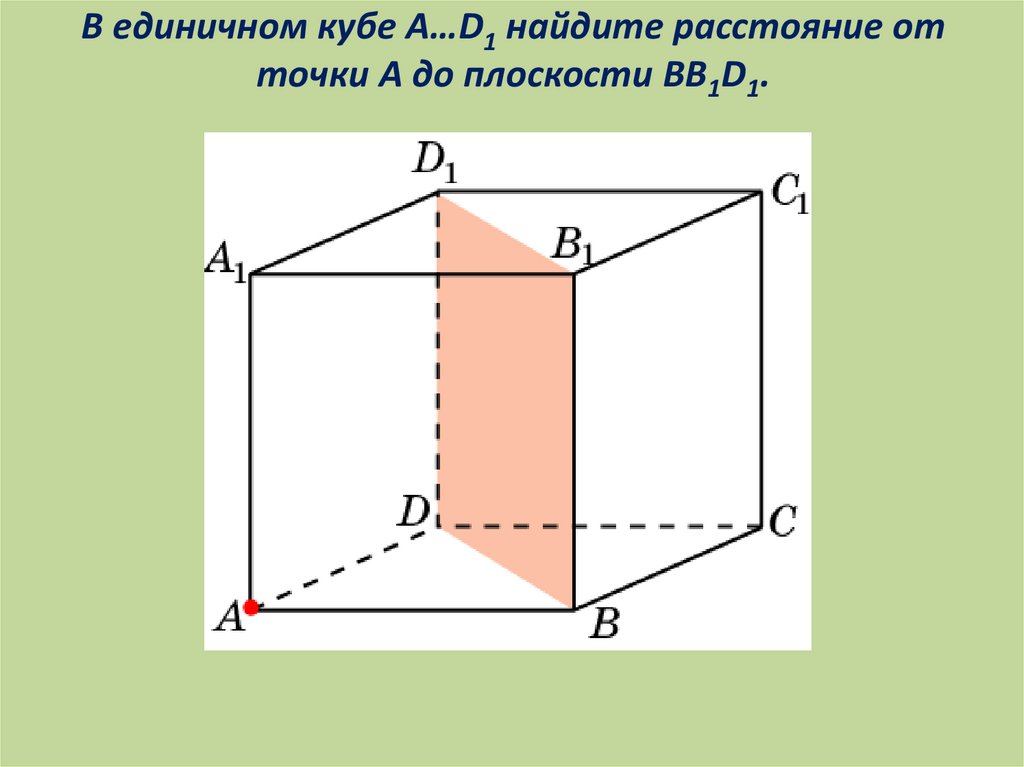
В единичном кубе A…D1 найдите расстояние отточки A до плоскости BB1D1.
12.
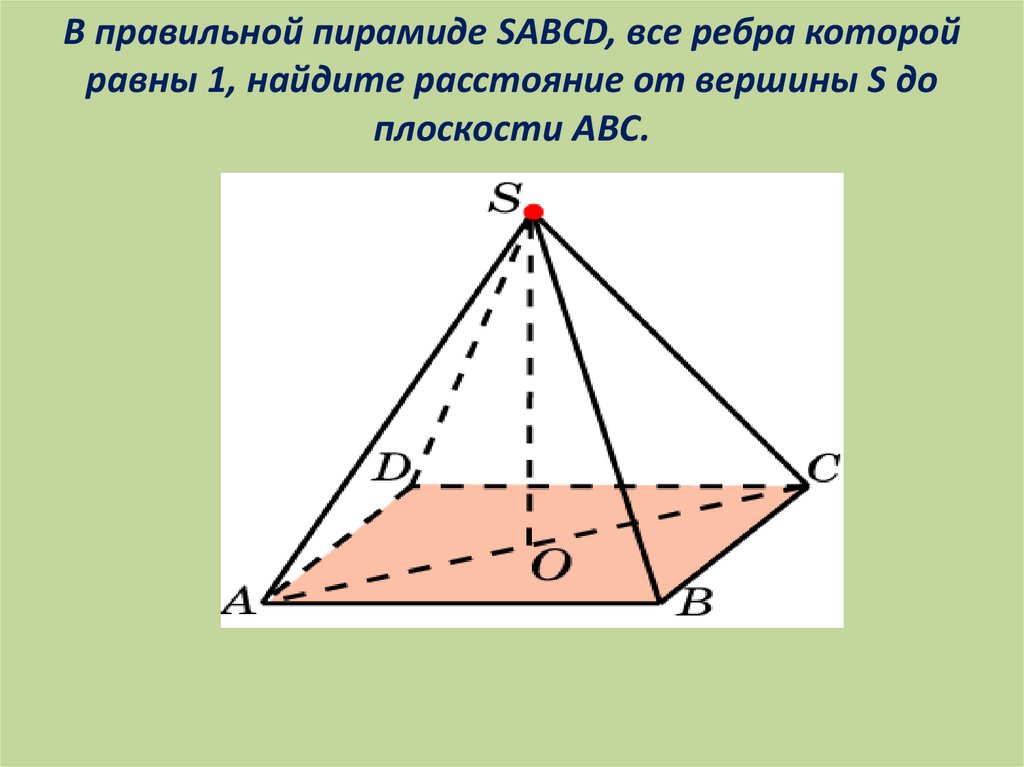
В правильной пирамиде SABCD, все ребра которойравны 1, найдите расстояние от вершины S до
плоскости ABC.
13.
Задачи для самостоятельного решения1.В правильном тетраэдре ABCD найдите расстояние от
вершины D до плоскости ABC.
2.В правильной 6-ой пирамиде SABCDEF, боковые ребра
которой равны 2, а ребра основания – 1, найдите
расстояние от вершины S до плоскости ABC.
3. В правильной 6-й призме A…F1, ребра которой равны 1,
найдите расстояние от точки A до плоскости CFF1.
4. В правильной 6-й призме A…F1, ребра которой равны 1,
найдите расстояние от точки A до плоскости BA1E1.
5.В правильной 6-й призме A…F1, ребра которой равны 1,
найдите расстояние от точки A до плоскости A1B1D.
14.
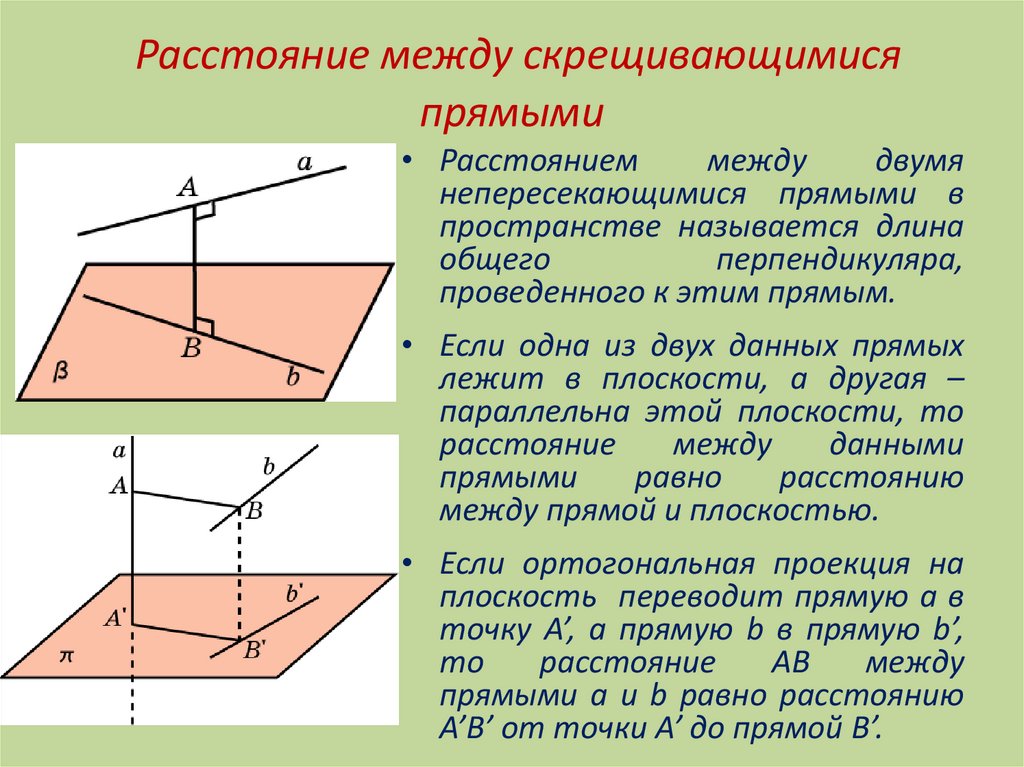
Расстояние между скрещивающимисяпрямыми
• Расстоянием
между
двумя
непересекающимися прямыми в
пространстве называется длина
общего
перпендикуляра,
проведенного к этим прямым.
• Если одна из двух данных прямых
лежит в плоскости, а другая –
параллельна этой плоскости, то
расстояние
между
данными
прямыми
равно
расстоянию
между прямой и плоскостью.
• Если ортогональная проекция на
плоскость переводит прямую a в
точку A’, а прямую b в прямую b’,
то
расстояние
AB
между
прямыми a и b равно расстоянию
A’B’ от точки A’ до прямой B’.
15.
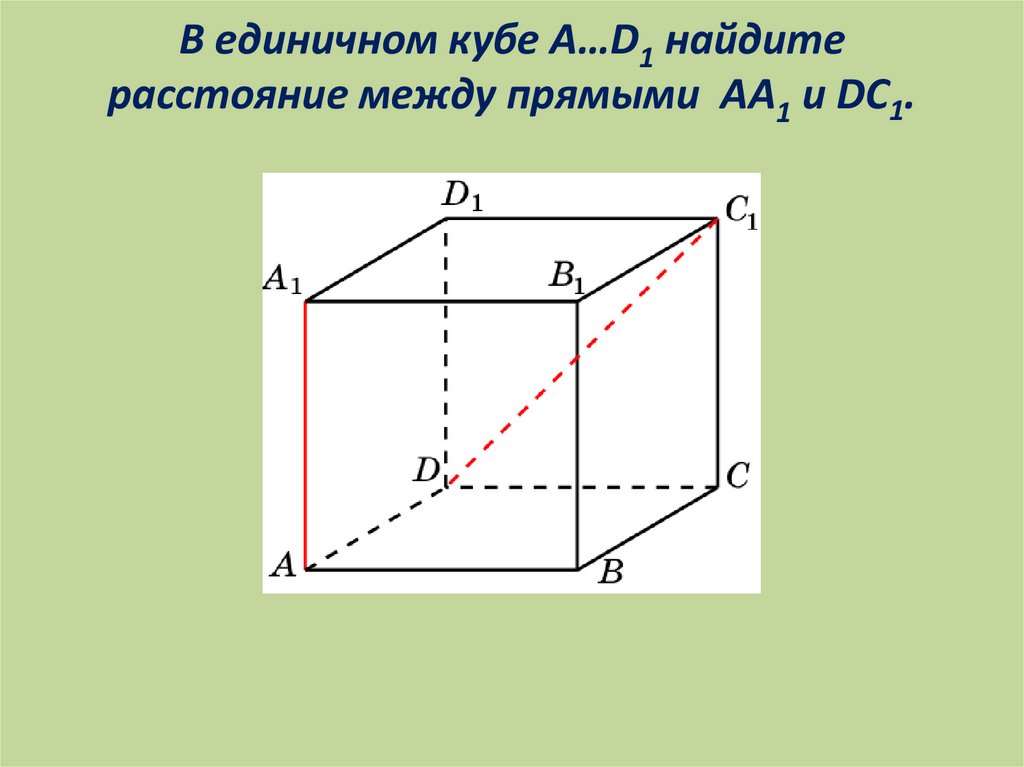
В единичном кубе A…D1 найдитерасстояние между прямыми AA1 и DC1.
16.
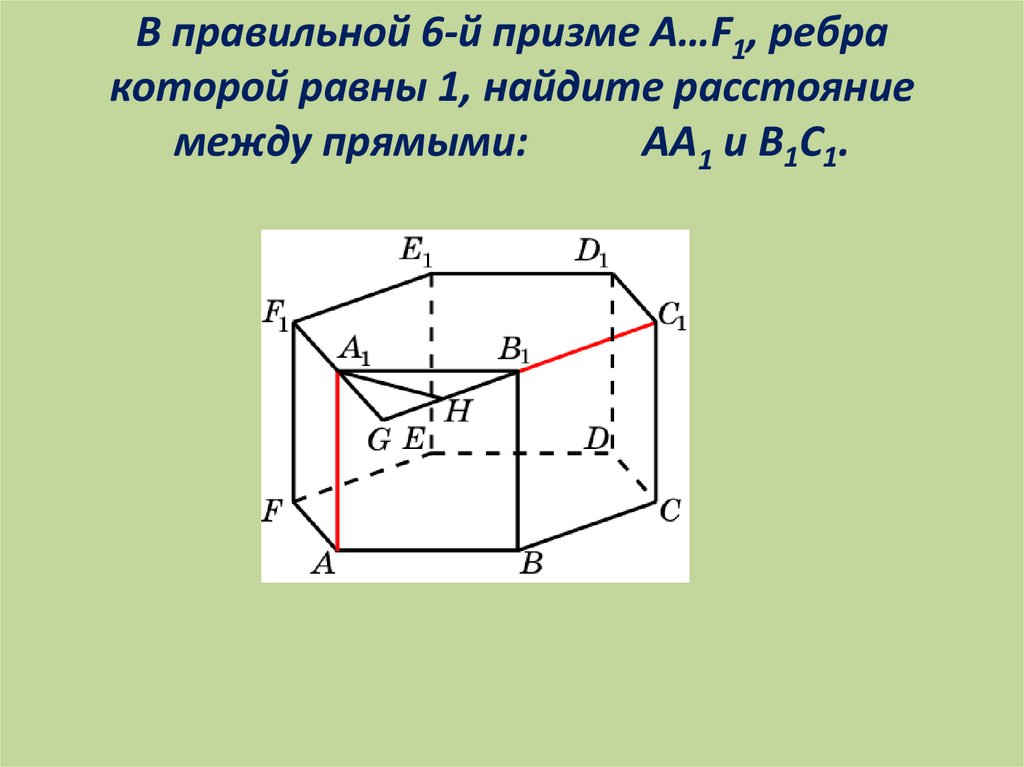
В правильной 6-й призме A…F1, ребракоторой равны 1, найдите расстояние
между прямыми:
AA1 и B1C1.
17.
Задачи для самостоятельного решения1.В правильной четырехугольной пирамиде SABCD, все
ребра которой равны 1, найдите расстояние между
прямыми BD и SA.
2.В пирамиде DABC известны длины ребер: AB= AC=DB
= DC= 10, BC=DA =12. Найдите расстояние между
прямыми DA и ВС.
3.В правильной пирамиде SABCD, все ребра которой
равны 1, найдите расстояние между прямыми SA и
BC.
4. В правильной 6-й призме A…F1, ребра которой равны
1, найдите расстояние между прямыми AВ и BE.











 Математика
Математика








