Похожие презентации:
Расстояния в пространстве
1.
Расстоянияв пространстве
2.
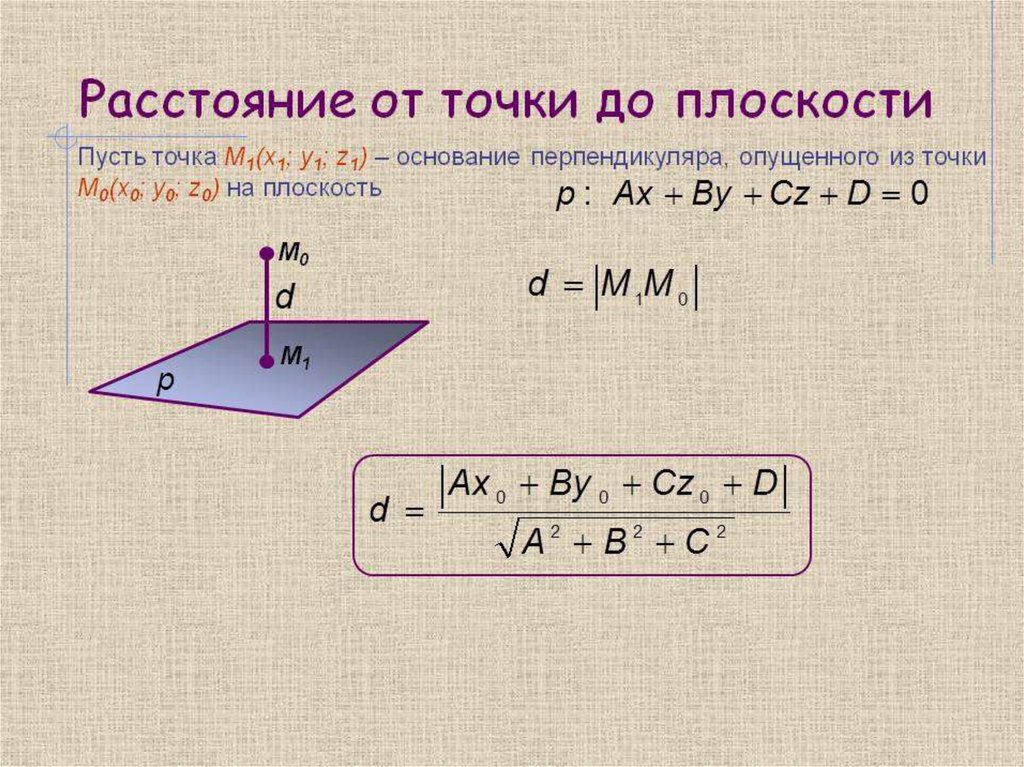
Цель урока:• 10.3.5 - уметь находить расстояние от
точки до плоскости и между
скрещивающимися прямыми;
3.
Актуализация знаний.1. Угол между прямыми равен 90˚. Как
называются такие прямые?
Ответ: перпендикулярные.
2. Верно ли утверждение: «Прямая называется
перпендикулярной плоскости, если она
перпендикулярна некоторой прямой,
лежащей в этой плоскости»
Ответ: да.
3. Сформулируйте признак
перпендикулярности прямой и
плоскости.
Ответ: прямая перпендикулярна
плоскости, если она перпендикулярна к
двум пересекающимся прямым,
лежащим в этой плоскости.
4.
Актуализация знаний.А
4. Что можно сказать о двух прямых,
перпендикулярных к одной плоскости?
М
Ответ: прямые параллельны.
5. Закончи предложение «
Ответ: параллельны.
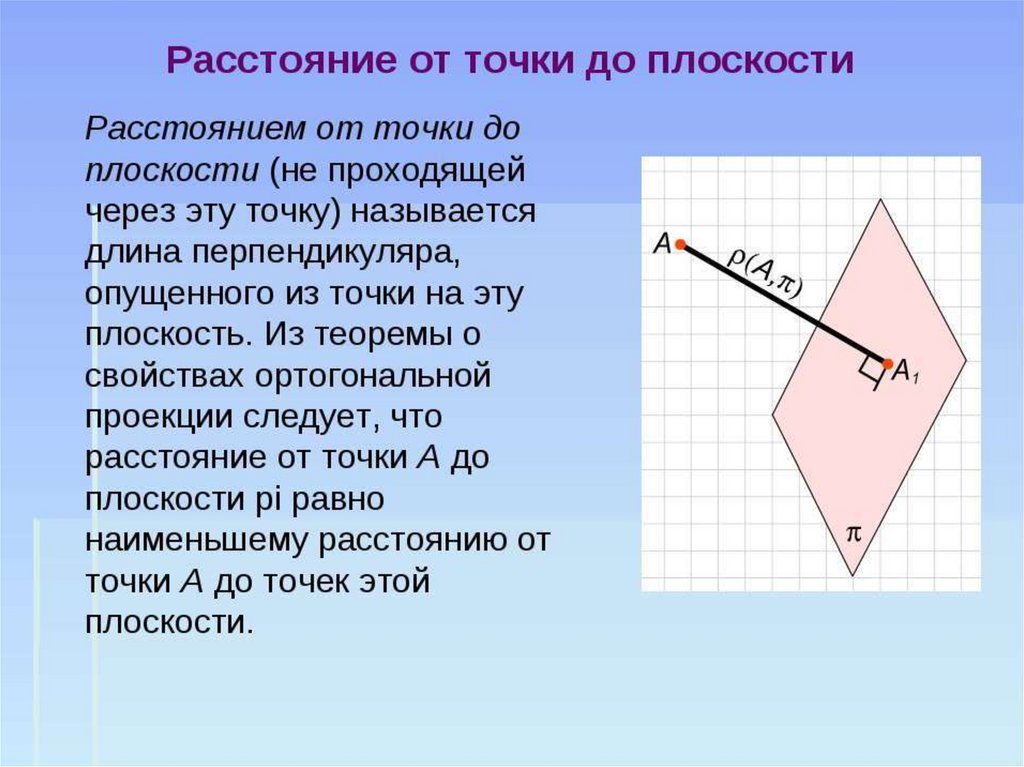
6. Как определяется расстояние от
точки до прямой на плоскости?
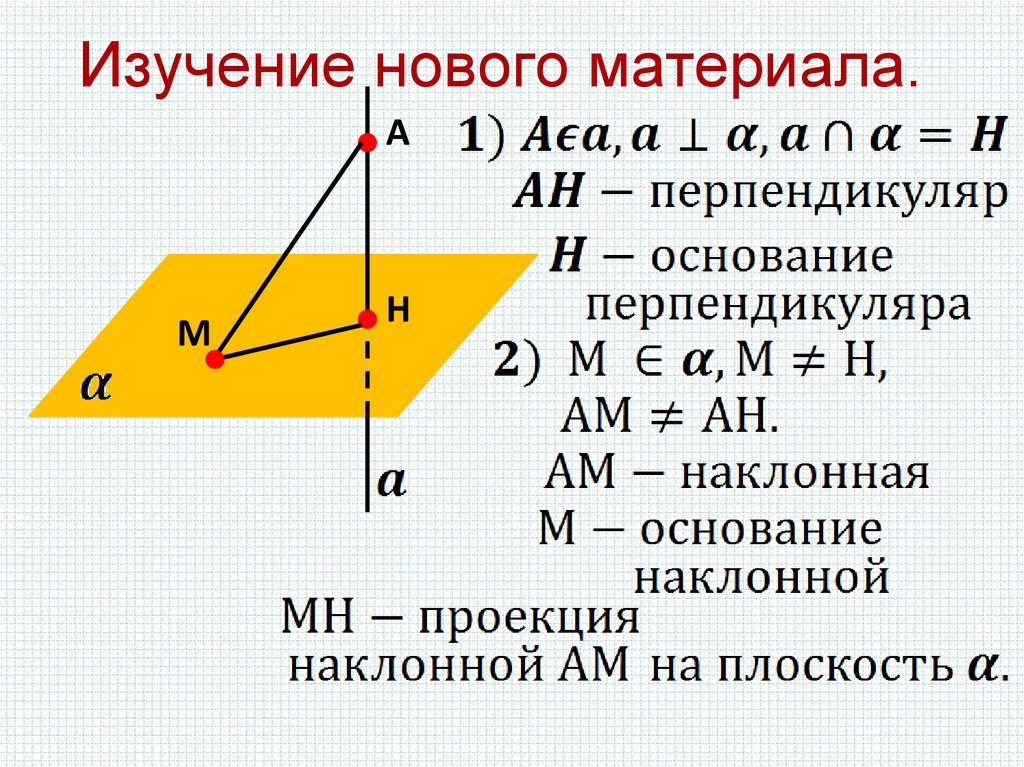
7. Вспомним, как называются
отрезки АМ, АН, точка М, точка
Н.
Н
5.
Изучение нового материала.А
М
Н
6.
7.
8.
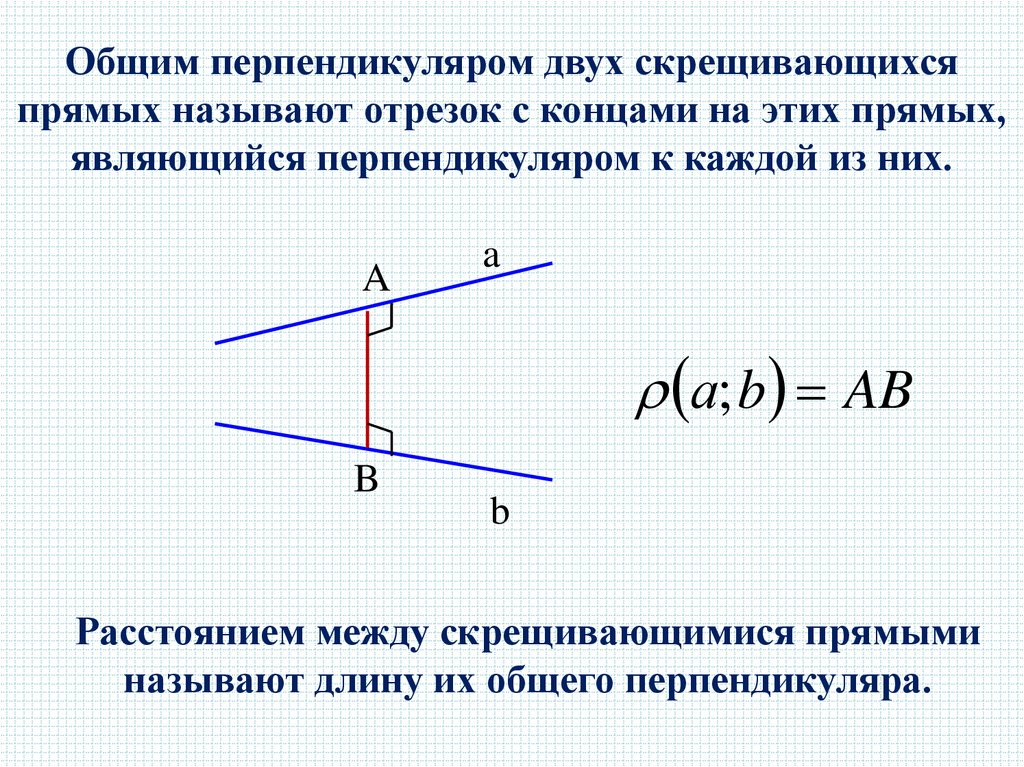
Общим перпендикуляром двух скрещивающихсяпрямых называют отрезок с концами на этих прямых,
являющийся перпендикуляром к каждой из них.
A
a
а; b AB
B
b
Расстоянием между скрещивающимися прямыми
называют длину их общего перпендикуляра.
9.
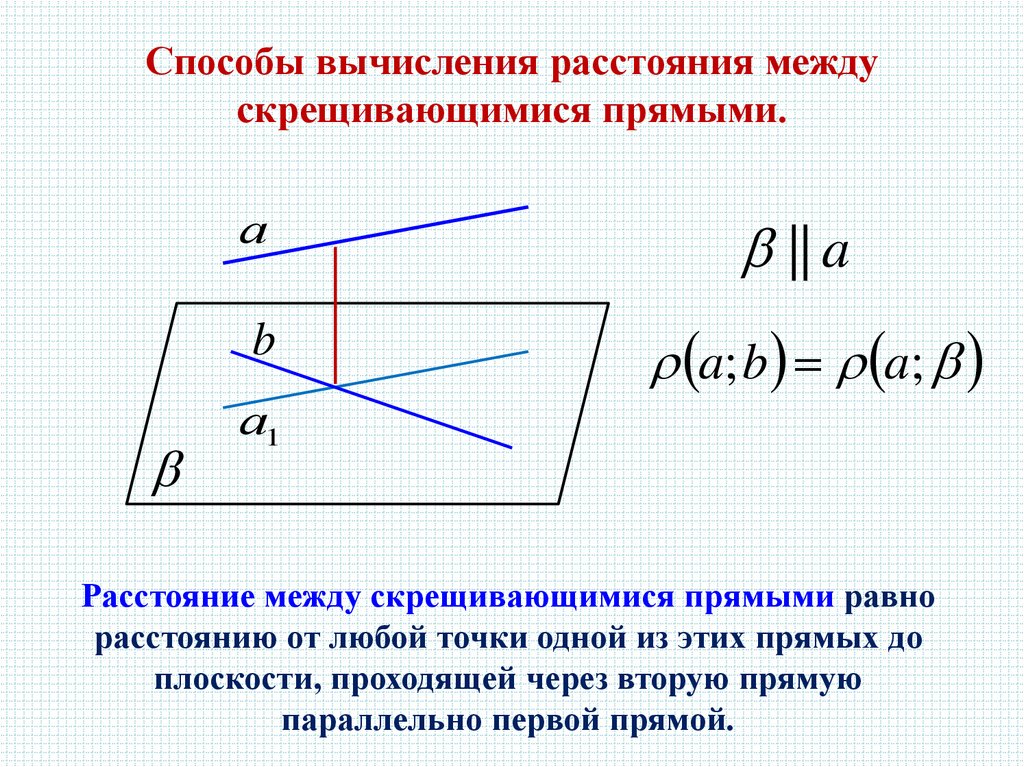
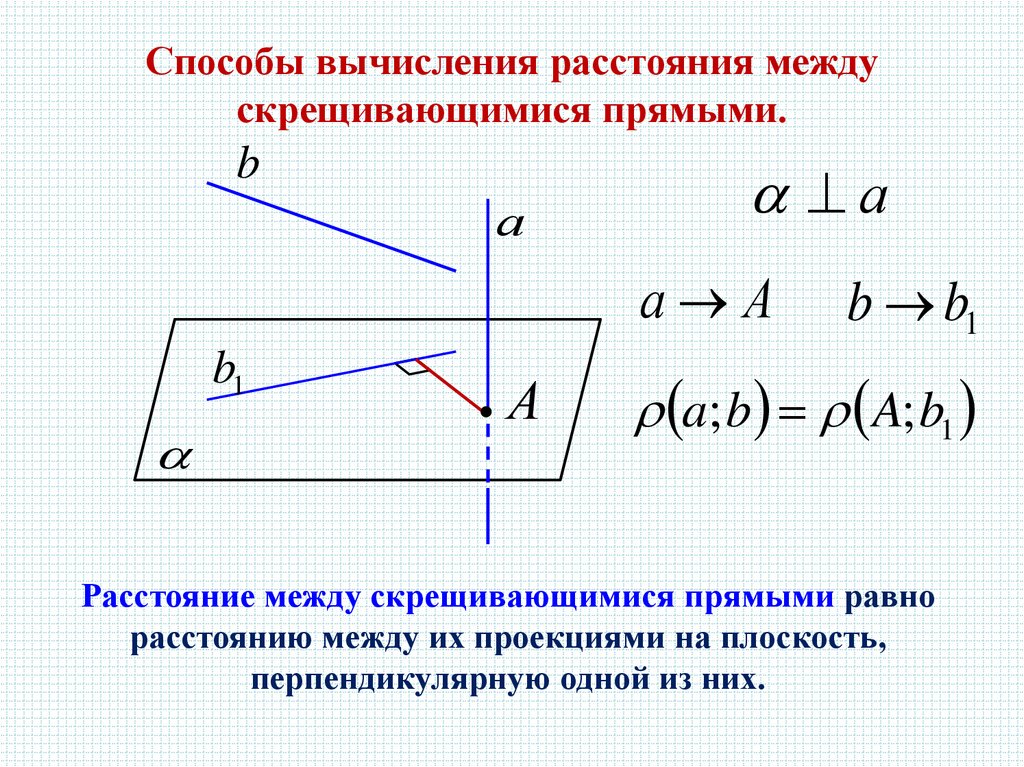
Способы вычисления расстояния междускрещивающимися прямыми.
а
|| a
b
a; b a;
а1
Расстояние между скрещивающимися прямыми равно
расстоянию от любой точки одной из этих прямых до
плоскости, проходящей через вторую прямую
параллельно первой прямой.
10.
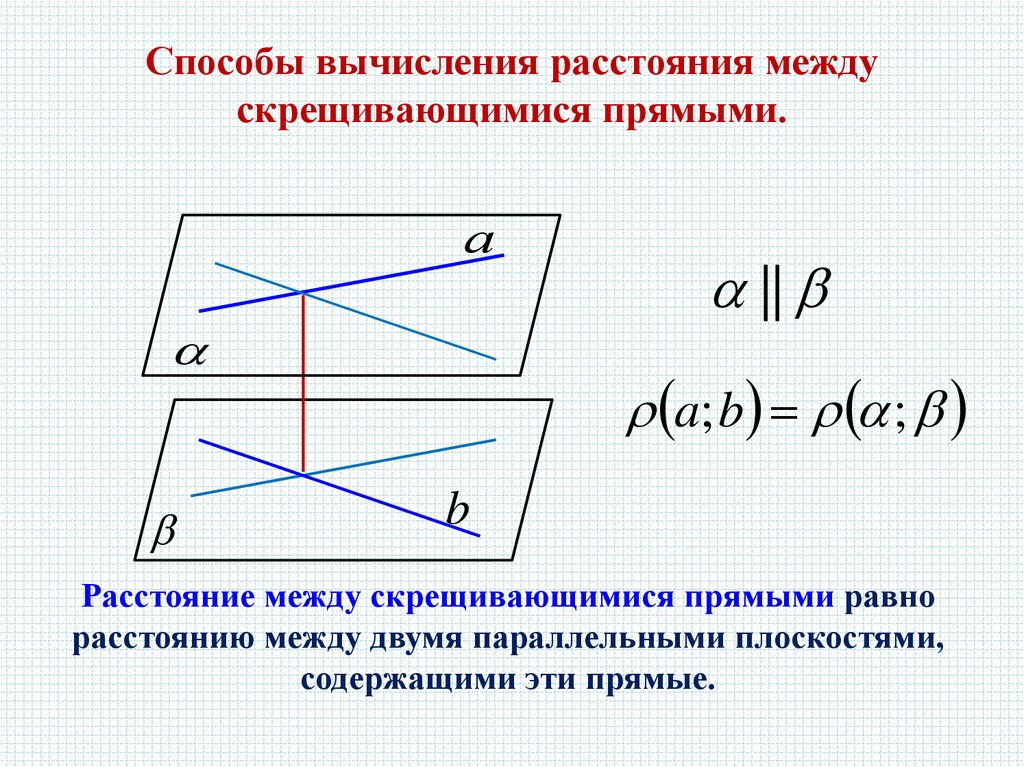
Способы вычисления расстояния междускрещивающимися прямыми.
а
||
a; b ;
b
Расстояние между скрещивающимися прямыми равно
расстоянию между двумя параллельными плоскостями,
содержащими эти прямые.
11.
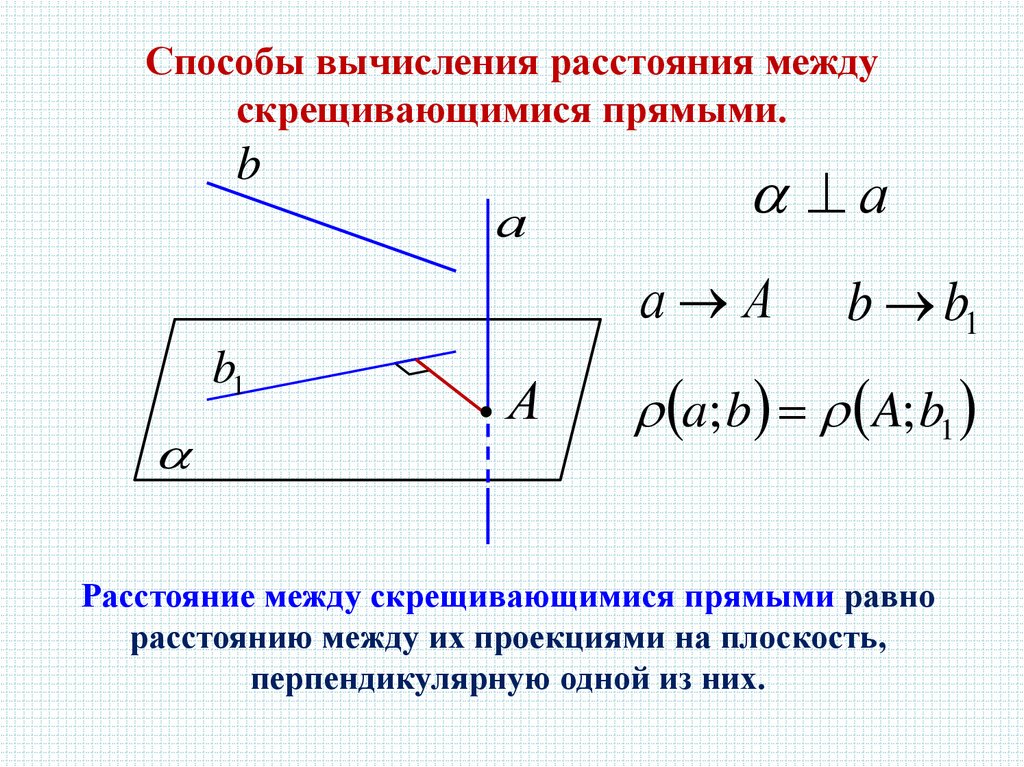
Способы вычисления расстояния междускрещивающимися прямыми.
b
а
а
а А
b1
А
b b1
a; b A; b1
Расстояние между скрещивающимися прямыми равно
расстоянию между их проекциями на плоскость,
перпендикулярную одной из них.
12.
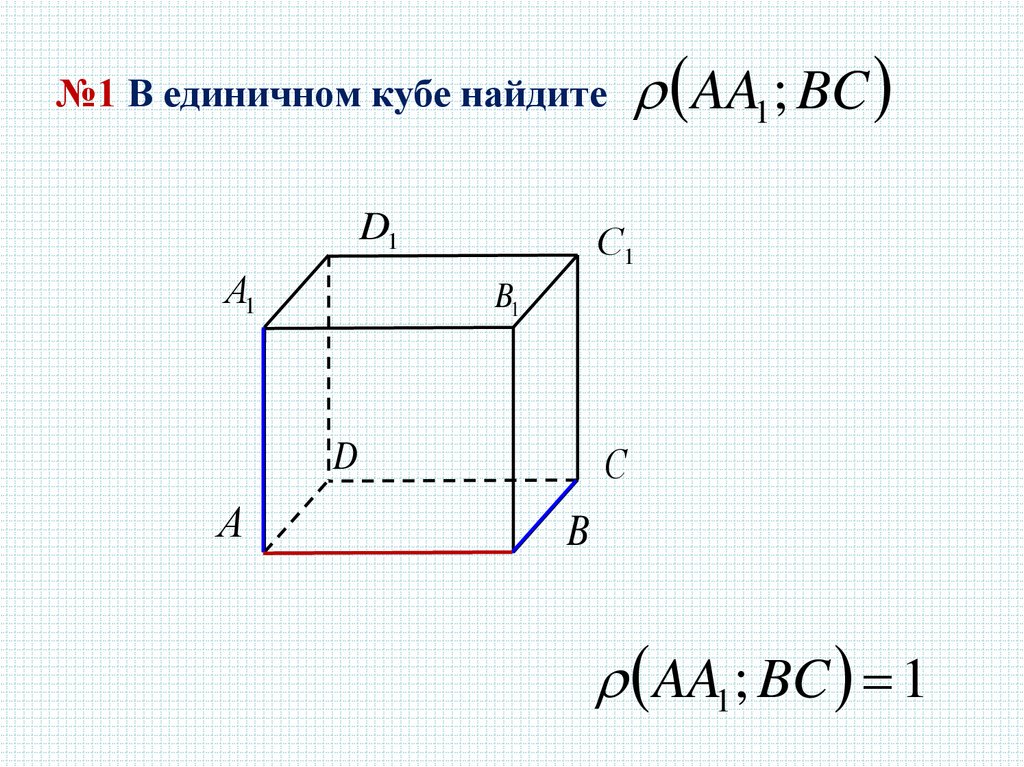
№1 В единичном кубе найдите AA1 ; BCD1
А1
С1
B1
С
D
А
B
AA1 ; BC 1
13.
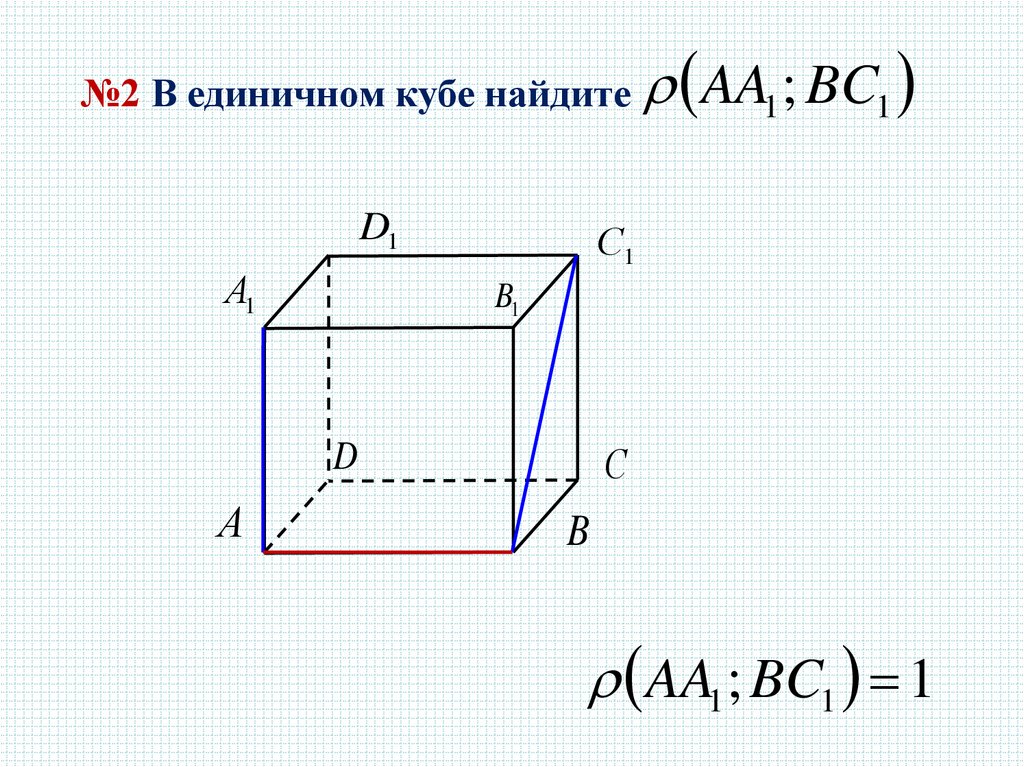
№2 В единичном кубе найдите AA1 ; BC1D1
А1
С1
B1
С
D
А
B
AA1 ; BC1 1
14.
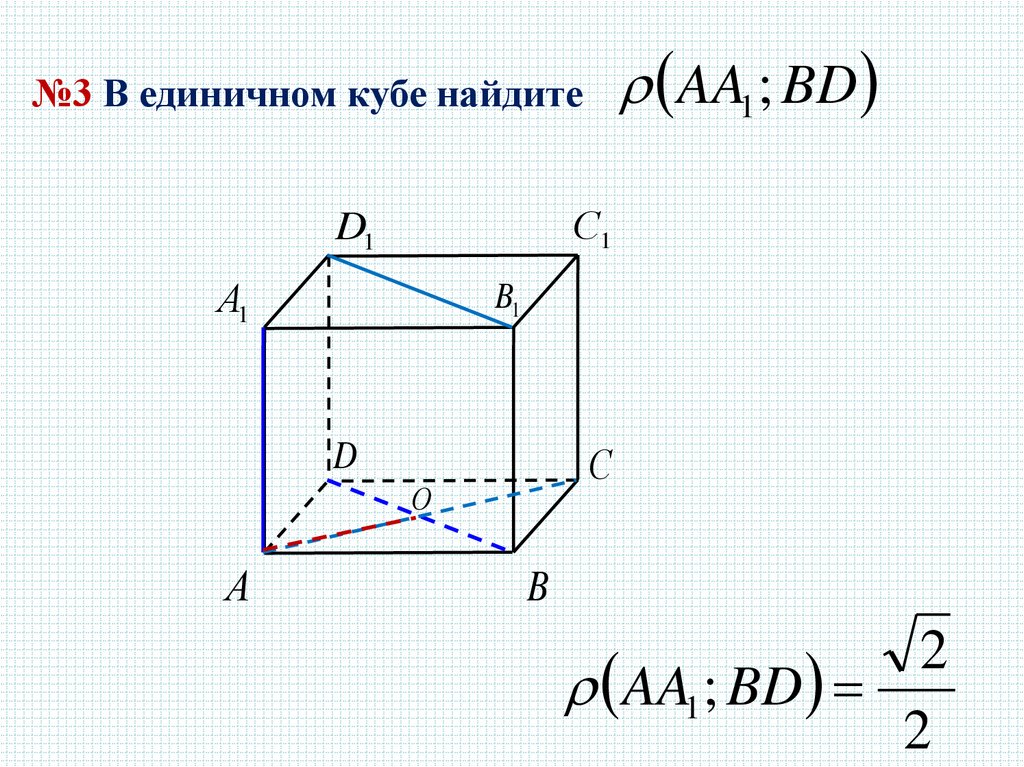
AA1 ; BD№3 В единичном кубе найдите
С1
D1
А1
B1
С
D
О
А
B
2
AA1 ; BD
2
15.
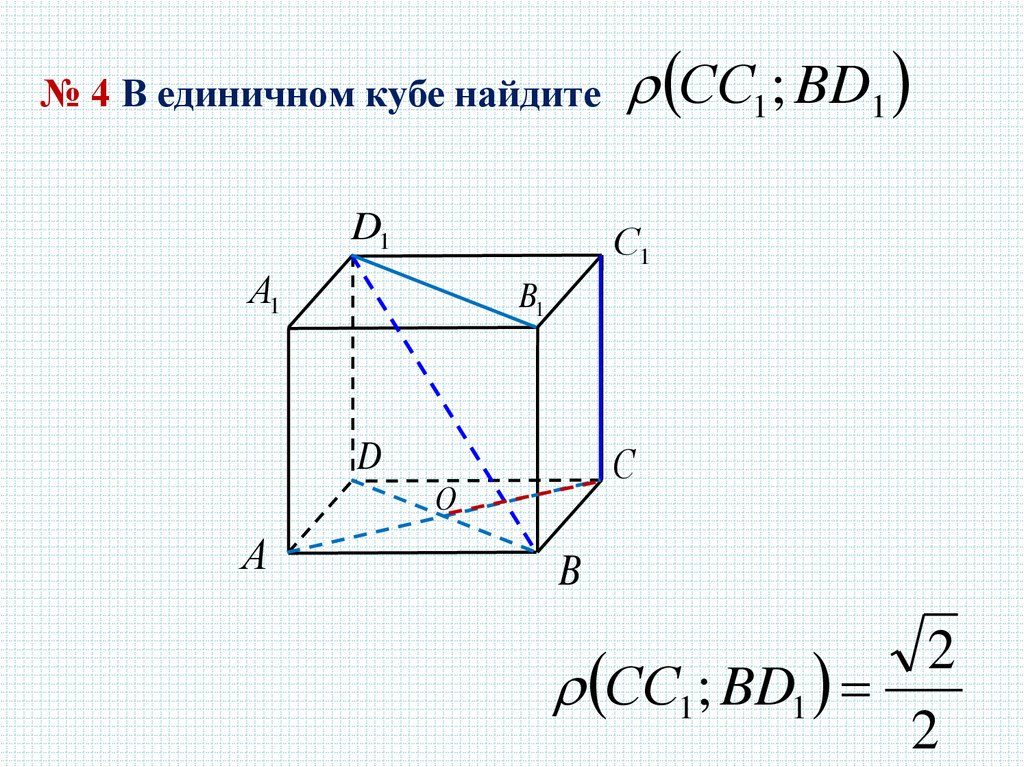
№ 4 В единичном кубе найдите СС1 ; BD1D1
С1
А1
B1
С
D
О
А
B
2
СС1 ; BD1
2
16.
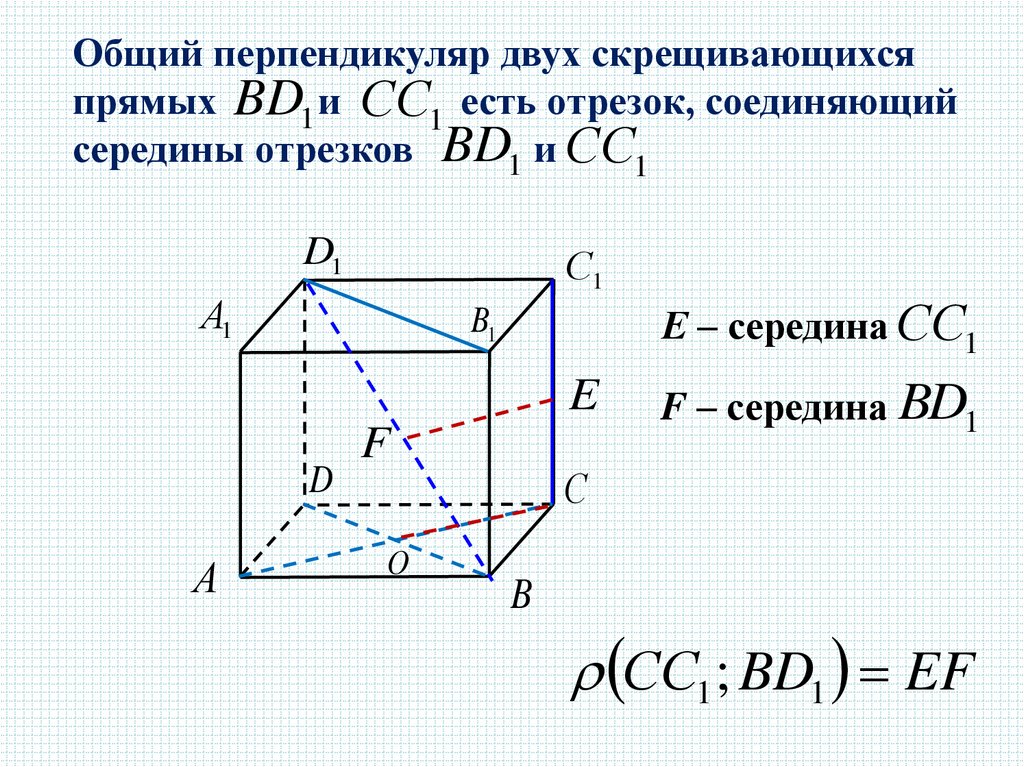
Общий перпендикуляр двух скрещивающихсяпрямых BD1 и СС1 есть отрезок, соединяющий
середины отрезков BD1 и СС1
D1
С1
А1
B1
E
D
А
F
О
Е – середина СС1
F – середина BD1
С
B
СС1 ; BD1 EF
17.
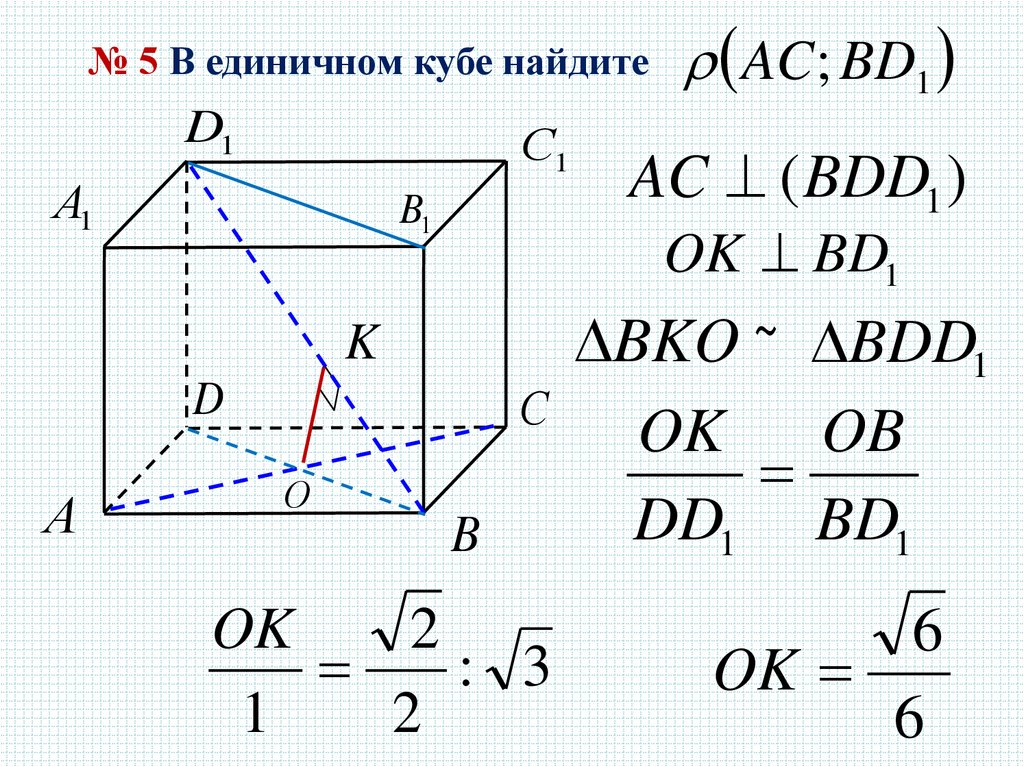
№ 5 В единичном кубе найдитеD1
С1
А1
B1
K
D
А
О
AC; BD1
AC ( BDD1 )
OK BD1
BKO ~ BDD1
С
OK
OB
DD1 BD1
B
OK
2
: 3
1
2
6
OK
6
18.
Способы вычисления расстояния междускрещивающимися прямыми.
b
а
а
а А
b1
А
b b1
a; b A; b1
Расстояние между скрещивающимися прямыми равно
расстоянию между их проекциями на плоскость,
перпендикулярную одной из них.
19.
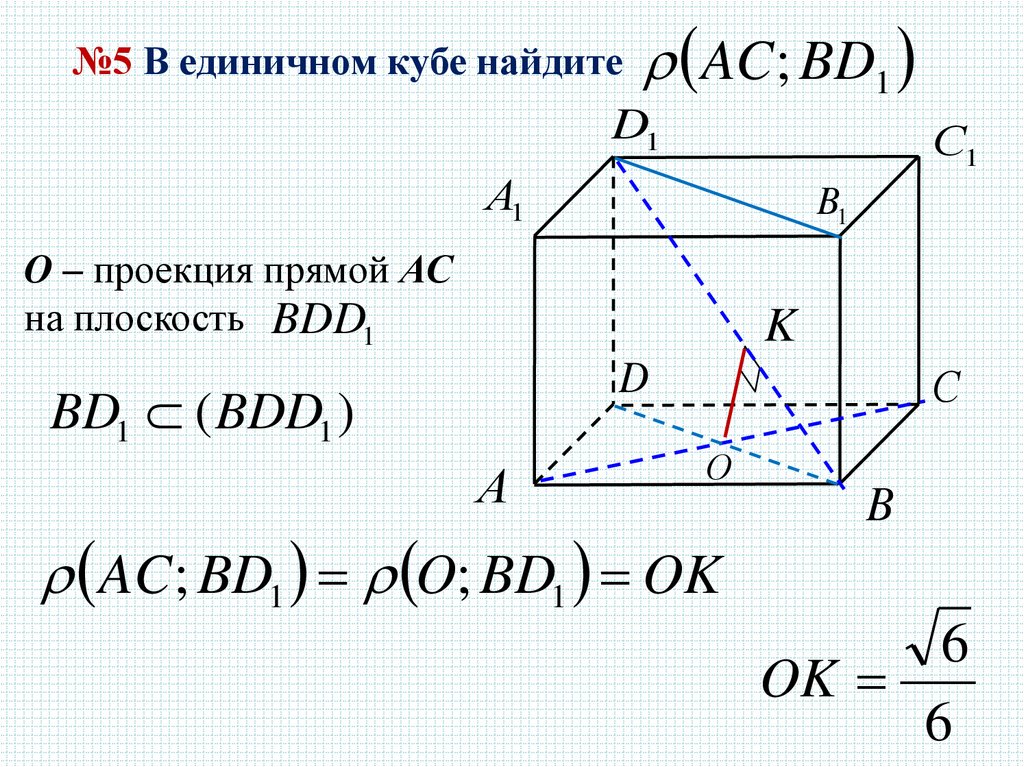
№5 В единичном кубе найдите AC ; BD1D1
С1
А1
B1
O – проекция прямой АС
на плоскость BDD1
K
С
D
BD1 ( BDD1 )
А
О
AC; BD1 O; BD1 OK
B
6
OK
6
20.
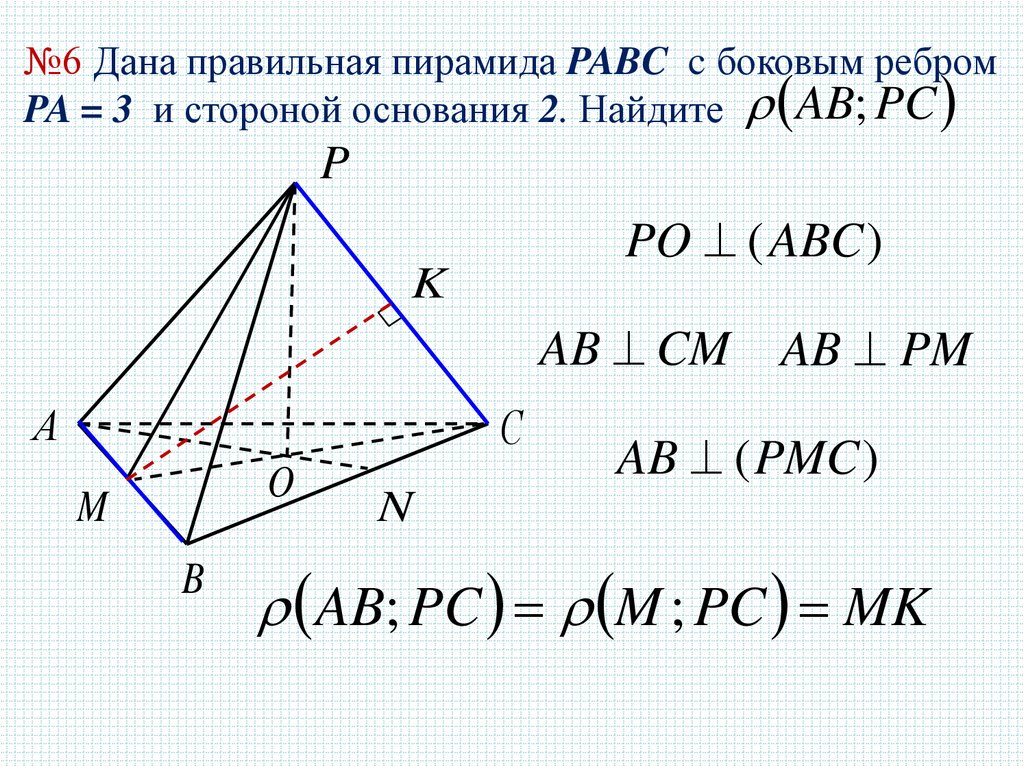
№6 Дана правильная пирамида PABC c боковым ребромPA = 3 и стороной основания 2. Найдите AB; PC
P
PO ( ABC )
K
AB CM AB PM
А
С
O
M
B
AB (PMC )
N
AB; PC M ; PC MK
21.
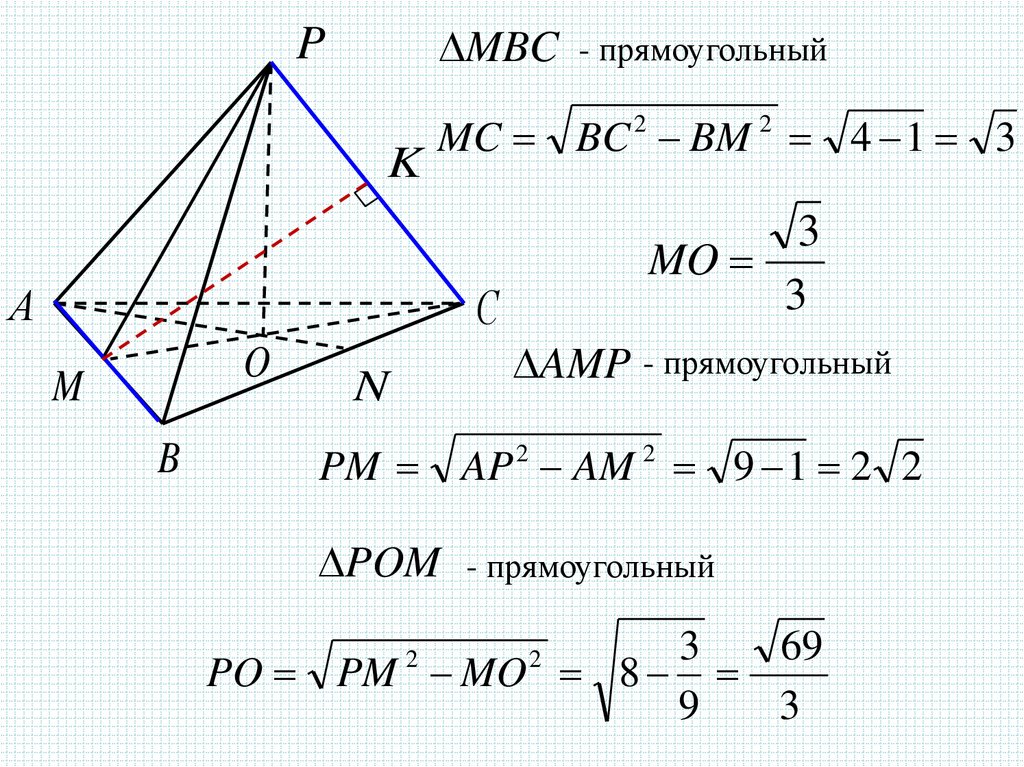
MBC - прямоугольныйP
K
А
MC BC 2 BM 2 4 1 3
С
O
M
B
N
3
MO
3
AMP - прямоугольный
PM AP 2 AM 2 9 1 2 2
POM - прямоугольный
3
69
PO PM MO 8
9
3
2
2
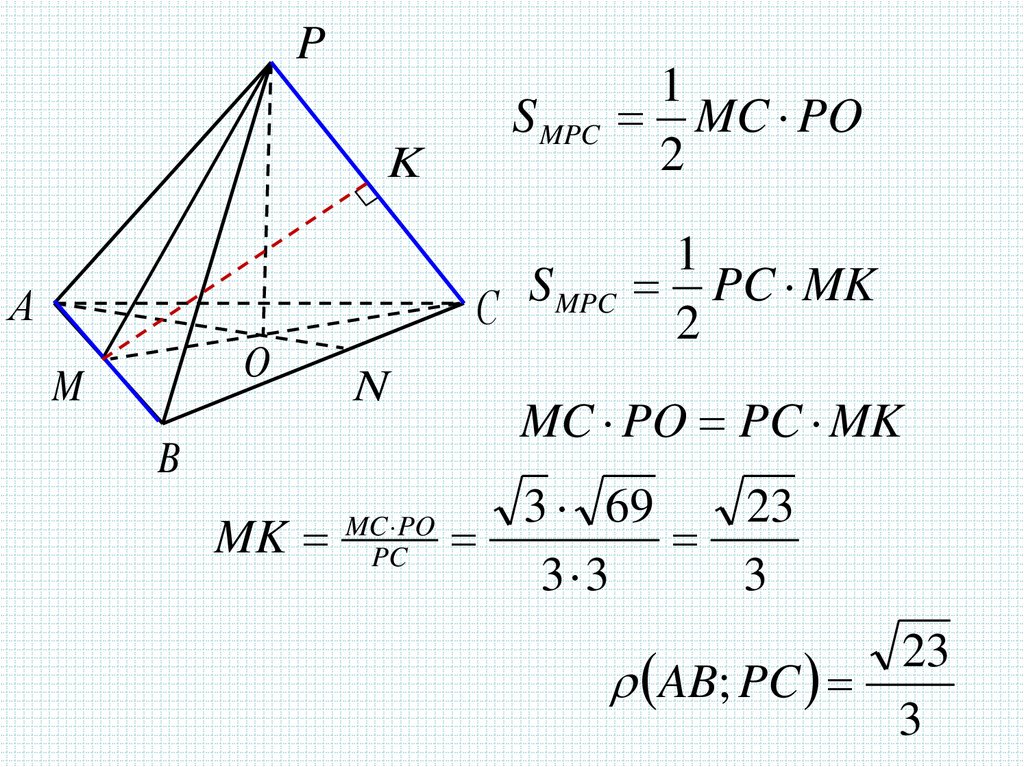
22.
PK
1
S
PC
MK
MPC
С
2
А
O
M
N
B
MK
1
S MPC MC PO
2
MC PO
PC
MC PO PC MK
3 69
23
3 3
3
23
AB; PC
3
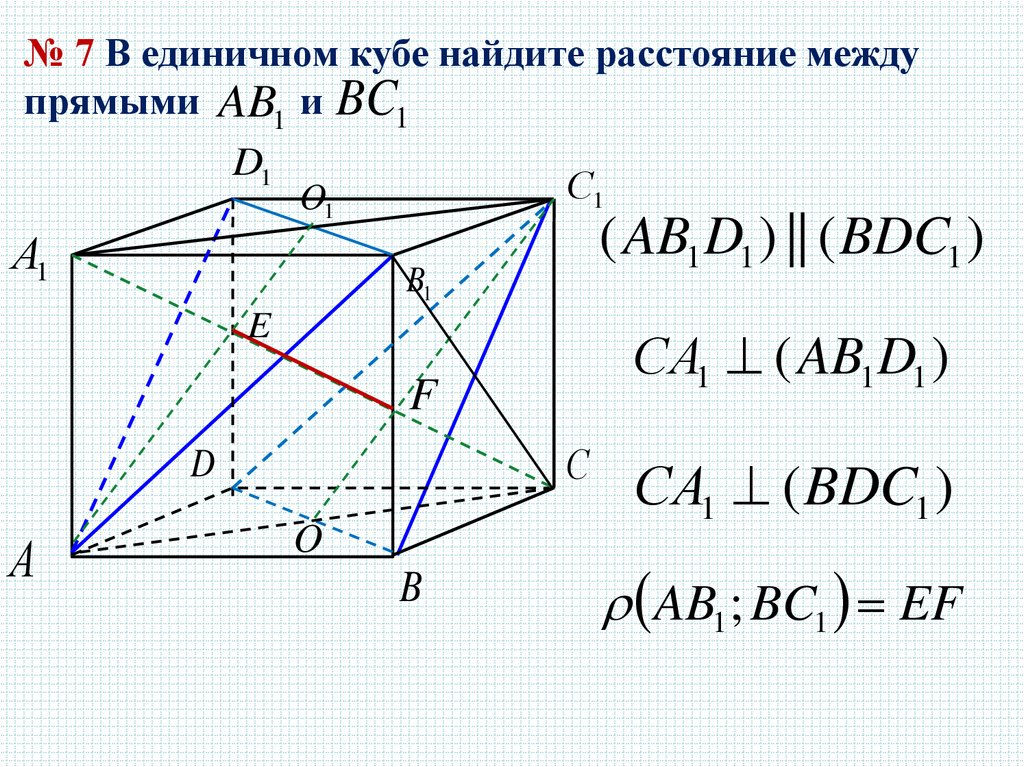
23.
№ 7 В единичном кубе найдите расстояние междупрямыми AB1 и BC1
D1
С1
O1
А1
( AB1 D1 ) || ( BDC1 )
B1
E
СA1 ( AB1 D1 )
F
С
D
А
O
B
СA1 ( BDC1 )
AB1 ; BC1 EF
24.
O1А1
F
E
А
AO1 || OC1
С1
С
O
A1O1 O1C1
A1 E EF
AO OC
EF FC
1
3
EF A1C
3
3
3
AB1 ; BC1
3
25.
Самостоятельная работа.Дана правильная пирамида PABC
c боковым ребром PA = 5 и
стороной основания 3. Найдите AB; PC
26.
Домашнее задание•Выучить все определения и
теоремы.
Параграф 2.2.3.-2.2.4 стр 44
№ 2.34 стр 46
Учебник «Геометрия 10»
Шыныбеков А.Н. 2019 год
.




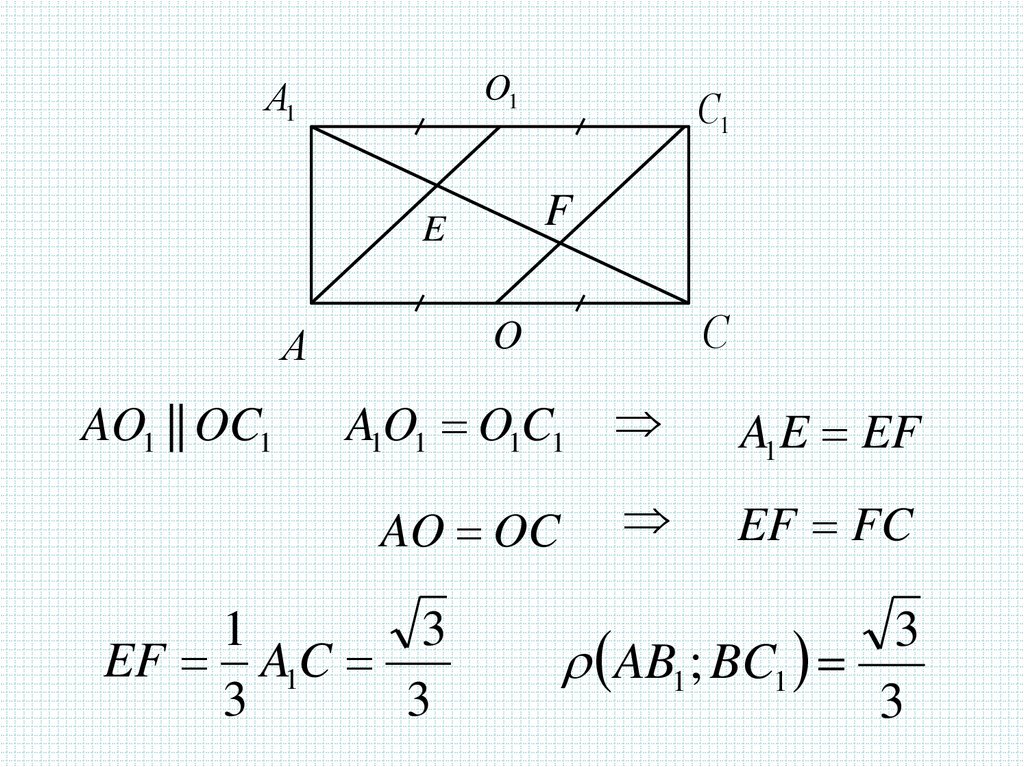


 Математика
Математика








