Метод Ньютона. Геометрическая иллюстрация метода Ньютона

1.

Метод Ньютона

2.

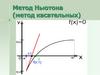
Геометрическая иллюстрация метода
Ньютона

3.

Суть метода Ньютона
Пусть корень уравнения f(x)=0 отделен на отрезке [a;b], причем первая
и вторая производные f’(x) и f''(x) непрерывны и знакопостоянны при х
[a;b].
В этом случае для построения последовательности приближений к
корню может быть использован метод Ньютона: каждое следующее
приближение xn вычисляется через предыдущее приближение xn–1 по
формуле:
f(x n 1 )
x n x n 1
f' (x n 1 )
Таким образом, задавшись начальным приближением x0 можно
получить первое приближение
f(x 0 )
x1 x 0
f' (x 0 )
затем второе
f(x 1 )
x 2 x1
f' (x 1 )
и так далее до получения приближения, погрешность которого не превышает
заданную.

4.

5.

Теорема о сходимости метода Ньютона
Пусть корень уравнения f(x) = 0 отделен на отрезке [a;b] (функция f(x)
непрерывна на [a;b] и на концах его принимает разные знаки), а производные
f'(x) и f''(x) отличны от нуля и сохраняют постоянные знаки на [a;b]. Тогда,
если выбрать начальное приближение х0 [a;b] так, чтобы f'(x0) ∙ f''(x0) > 0, то
последовательность приближений, определяемая формулой
f(x n 1 )
x n x n 1
f' (x n 1 )
сходится.

6.

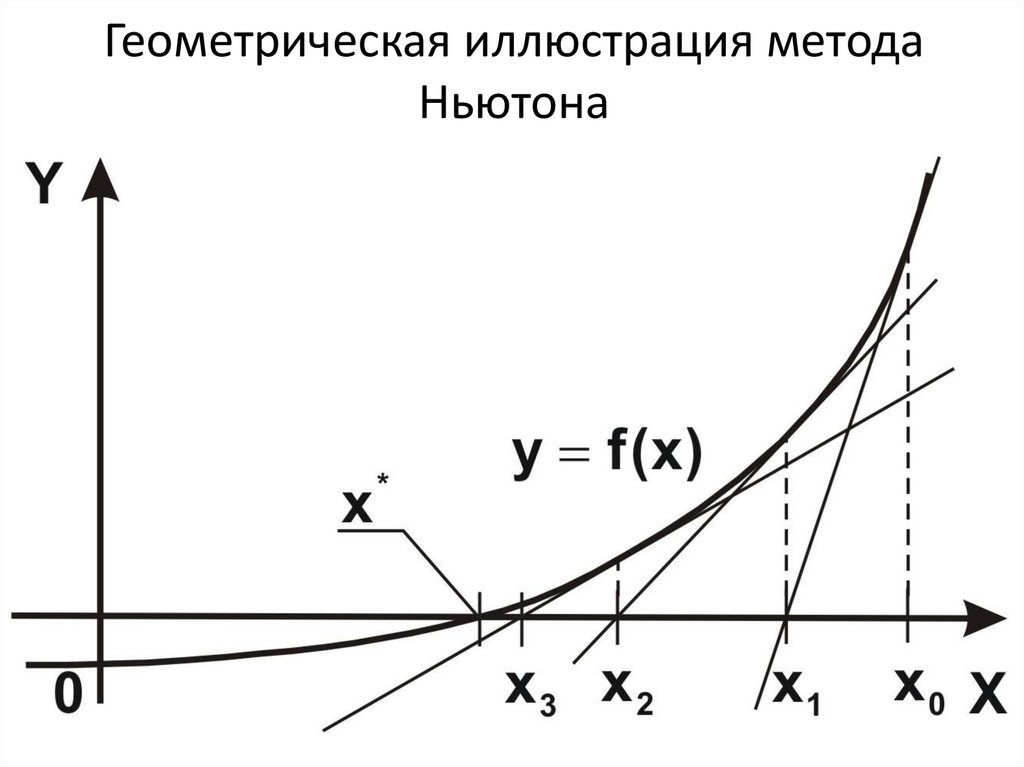
f'(x) и f''(x) не знакопостоянны

7.

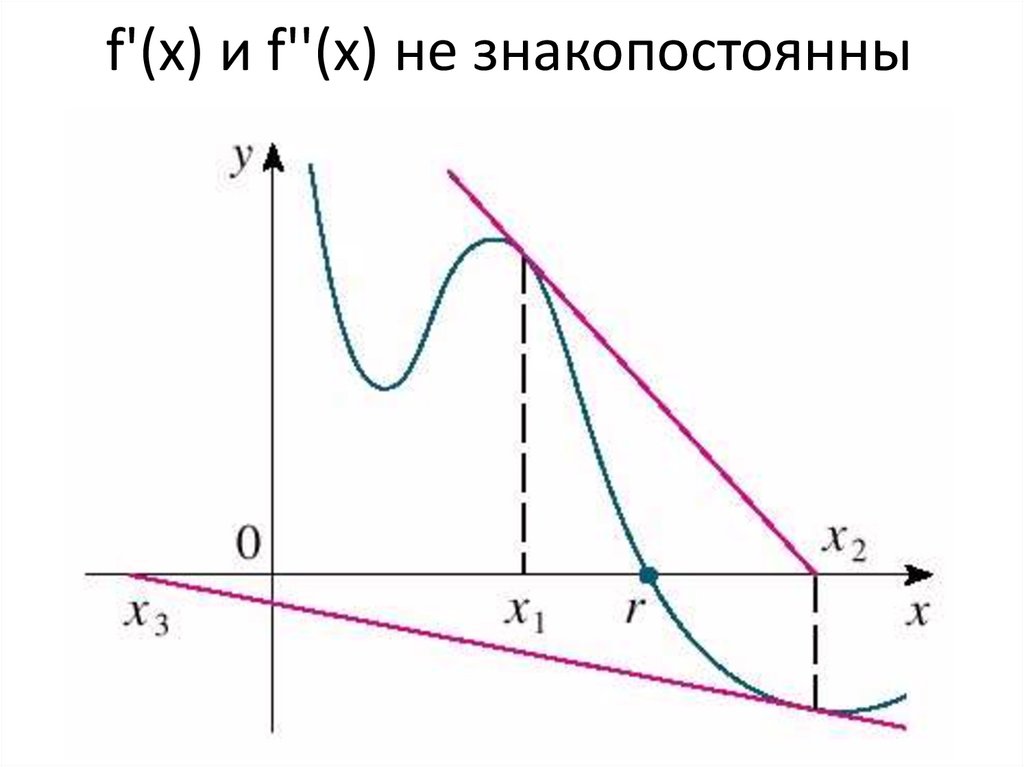
Схема алгоритма метода Ньютона

8.

Оценка погрешности приближения для метода
Ньютона
Можно показать, что погрешность n–го приближения
| x n x* |
M2
(x n x n 1 ) 2
2 m1
где m1 – наименьшее значение |f'(x)| при x [a; b];
M2 – наибольшее значение |f’’(x)| при x [a; b].
Таким образом, если задана допустимая погрешность приближения к корню
ε, то процесс последовательных приближений можно прекратить при
выполнении условия:
2 m 1ε
| x n x n 1 |
M2
Существует и другой, универсальный способ оценки погрешности
приближения и соответствующее ему правило останова. Этот способ
применим к любому методу уточнения корня, но требует дополнительного
вычисления функции в точке очередного приближения:
| f(x n ) |
ε
m1
где m1 – наименьшее значение |f'(x)| при x [a; b].

9.

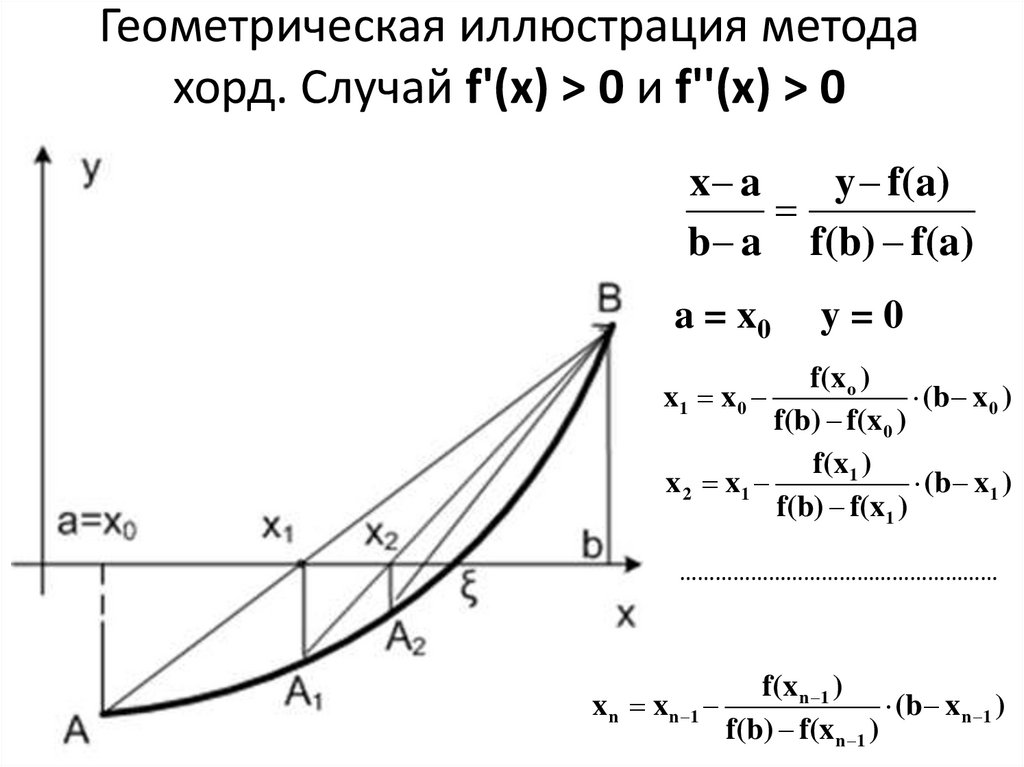
Геометрическая иллюстрация метода
хорд. Случай f'(x) > 0 и f''(x) > 0
x a
y f(a)
b a f(b) f(a)
a = x0
y=0
f(x o )
(b x 0 )
f(b) f(x 0 )
f(x1 )
x 2 x1
(b x1 )
f(b) f(x1 )
x1 x 0
………………………………………………
x n x n 1
f(x n 1 )
(b x n 1 )
f(b) f(x n 1 )

10.

Геометрическая иллюстрация метода
хорд. Случай f'(x) > 0 и f''(x) < 0
b x
f(b) y
b a f(b) f(a)
b = x0
y=0
f(x o )
(x 0 a)
f(x 0 ) f(a)
f(x1 )
x 2 x1
(x1 a)
f(x1 ) f(a)
x1 x 0
………………………………………………
x n x n 1
f(x n 1 )
(xn 1 a)
f(x n 1 ) f(a)