Цифровая схемотехника и архитектура компьютера. Проектирование последовательностной логики. (Глава 3)

1.

Глава 3
Цифровая схемотехника и архитектура
компьютера, второе издание
Дэвид М. Харрис и Сара Л. Харрис
Глава 3 <1>

2.

Цифровая схемотехника и архитектура компьютера
Эти слайды предназначены для преподавателей, которые читают
лекции на основе учебника «Цифровая схемотехника и
архитектура компьютера» авторов Дэвида Харриса и Сары
Харрис. Бесплатный русский перевод второго издания этого
учебника можно загрузить с сайта компании Imagination
Technologies:
https://community.imgtec.com/downloads/digital-design-andcomputer-architecture-russian-edition-second-edition
Процедура регистрации на сайте компании Imagination
Technologies описана на станице:
http://www.silicon-russia.com/2016/08/04/harris-and-harris-2/
Глава 3 <2>

3.

Благодарности
Перевод данных слайдов на русский язык был выполнен командой
сотрудников университетов и компаний из России, Украины, США в составе:
Александр Барабанов - доцент кафедры компьютерной инженерии факультета радиофизики,
электроники и компьютерных систем Киевского национального университета имени Тараса
Шевченко, кандидат физ.-мат. наук, Киев, Украина;
Антон Брюзгин - начальник отдела АО «Вибро-прибор», Санкт-Петербург, Россия.
Евгений Короткий - доцент кафедры конструирования электронно-вычислительной аппаратуры
факультета электроники Национального технического университета Украины «Киевский
Политехнический Институт», руководитель открытой лаборатории электроники Lampa, кандидат
технических наук, Киев, Украина;
Евгения Литвинова – заместитель декана факультета компьютерной инженерии и управления,
доктор технических наук, профессор кафедры автоматизации проектирования вычислительной
техники Харьковского национального университета радиоэлектроники, Харьков, Украина;
Юрий Панчул - старший инженер по разработке и верификации блоков микропроцессорного
ядра в команде MIPS I6400, Imagination Technologies, отделение в Санта-Кларе, Калифорния, США;
Дмитрий Рожко - инженер-программист АО «Вибро-прибор», магистр Санкт-Петербургского
государственного автономного университета аэрокосмического приборостроения (ГУАП), СанктПетербург, Россия;
Владимир Хаханов – декан факультета компьютерной инженерии и управления, проректор по
научной работе, доктор технических наук, профессор кафедры автоматизации проектирования
вычислительной техники Харьковского национального университета радиоэлектроники, Харьков,
Украина;
Светлана Чумаченко – заведующая кафедрой автоматизации проектирования вычислительной
техники Харьковского национального университета радиоэлектроники, доктор технических наук,
профессор, Харьков, Украина.
Глава 3 <3>

4.

Глава 3 :: Темы
• Введение
• Защелки и Триггеры
• Проектирование синхронных
логических схем
• Конечные автоматы
• Синхронизация
последовательностных схем
• Параллелизм
Глава 3 <4>

5.

Введение
• Выходы последовательностной схемы зависят
как от текущих, так и от прошлых значений
на входах - схема имеет память.
• Некоторые определения:
– Состояние: Вся информация о схеме, необходимая
для определения ее будущего поведения
– Защелки и Триггеры: Элементы, хранящие один
бит состояния
– Синхронные последовательностные схемы: За
комбинационной схемой следует набор триггеров
Глава 3 <5>

6.

Последовательностные схемы
• Выдают последовательность событий
• Имеют (краткосрочную) память
• Для сохранения информации используют
обратную связь с выходов на входы
Глава 3 <6>

7.

Элементы, хранящие состояние
• Состояние схемы влияет на ее будущее
поведение
• Элементы хранят состояние схемы
–
–
–
–
Бистабильная схема
RS-триггер
D-защелка
D-триггер
Глава 3 <7>

8.

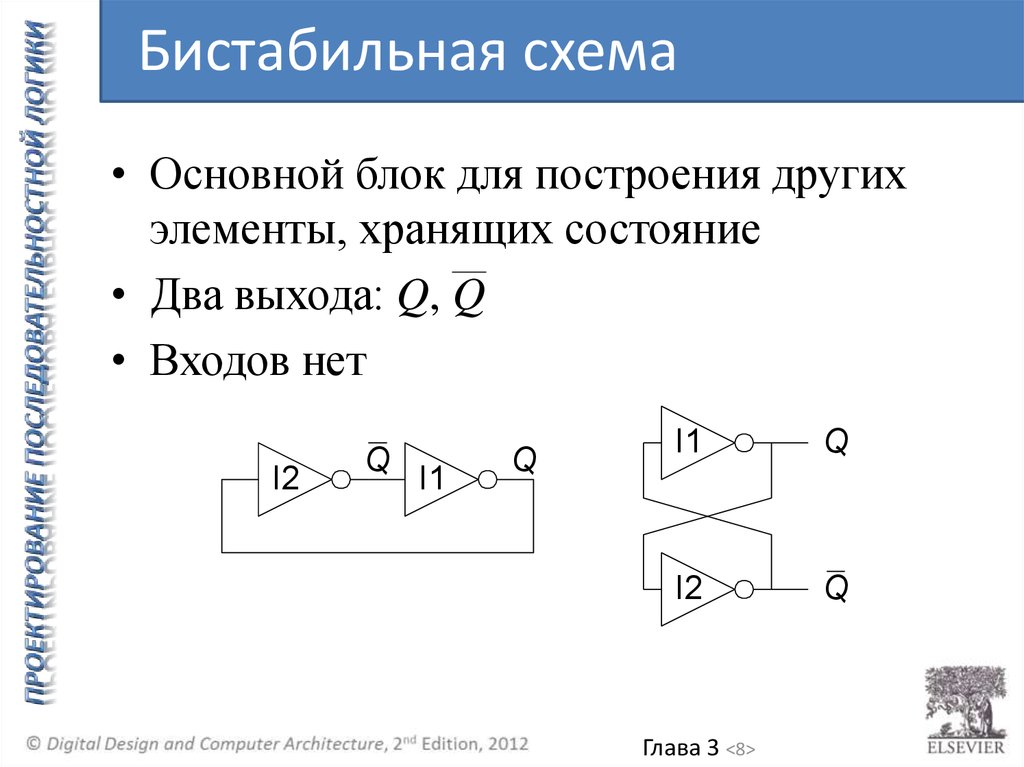
Бистабильная схема
• Основной блок для построения других
элементы, хранящих состояние
• Два выхода: Q, Q
• Входов нет
I2
Q
I1
Q
I1
Q
I2
Q
Глава 3 <8>

9.

Анализ бистабильной схемы
• Рассмотрим два возможных случая:
– Q = 0:
Тогда Q = 1, Q = 0
(нет противоречия)
– Q = 1:
Тогда Q = 0, Q = 1
(нет противоречия)
1
0
0
1
I1
I2
I1
I2
0
1
1
0
• Хранит 1 бит переменной состояния Q (или Q)
• Входы управления состоянием отсутствуют
Глава 3 <9>
Q
Q
Q
Q

10.

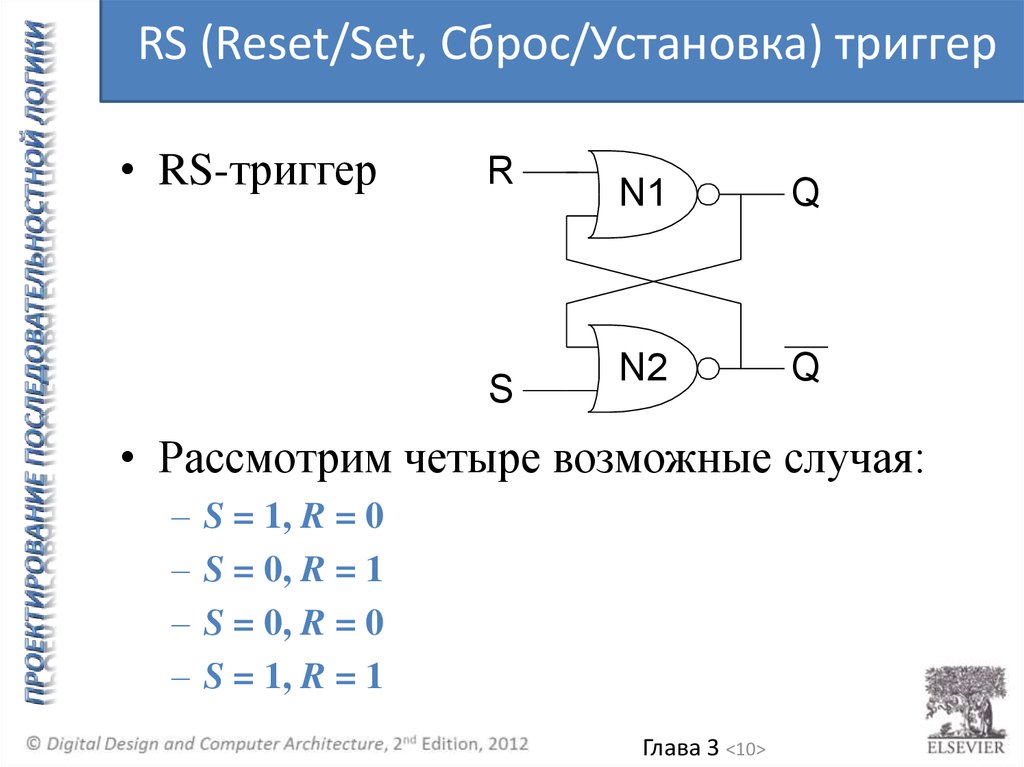
RS (Reset/Set, Сброс/Установка) триггер
• RS-триггер
R
S
N1
Q
N2
Q
• Рассмотрим четыре возможные случая:
–
–
–
–
S = 1, R = 0
S = 0, R = 1
S = 0, R = 0
S = 1, R = 1
Глава 3 <10>

11.

Анализ RS-триггера
– S = 1, R = 0:
Тогда Q = 1 и Q = 0
R
N1
1
Q
0
S
– S = 0, R = 1:
Тогда Q = 1 и Q = 0
0
R
0
1
N2
1
N1
0
0
Q
Q
1
S
0
0
N2
Глава 3 <11>
1
Q

12.

Анализ RS-триггера
– S = 0, R = 0:
Тогда Q = Qprev
Qprev = 0
R
S
– S = 1, R = 1:
Тогда Q = 0, Q = 0
0
0
N1
0
Qprev = 1
N2
R
Q
Q
R
S
1
N1
0
N1
0
0
N2
Q
0
S
0
1
N2
Глава 3 <12>
0
Q
1
Q
Q

13.

Анализ RS-триггера
– S = 0, R = 0:
Тогда Q = Qprev
– Память!
Qprev = 0
R
S
0
N1
0
N2
– S = 1, R = 1:
Тогда Q = 0, Q = 0
– Запрещенное состояние
Q ≠ NOT Q
Qprev = 1
0
Q
Q
R
R
S
1
N1
0
0
N1
Q
N2
Q
0
Q
0
S
0
1
N2
Глава 3 <13>
0
Q

14.

Обозначение RS-триггера
• RS обозначает триггер со входами Reset/Set,
Сброс/Установка
– Хранит один бит состояния (Q)
• Хранимое значение определяется входами S, R
– Set (Установка):
SR Latch
Устанавливает выход в 1
Symbol
(S = 1, R = 0, Q = 1)
– Reset (Сброс):
R Q
Устанавливает выход в 0
(S = 0, R = 1, Q = 0)
S
Q
• Нужно предпринять специальные меры для
исключения появления запрещенного состояния (S = R = 1)
Глава 3 <14>

15.

D-защелка
• Два входа CLK, D
– CLK: определяет когда выход изменяется
– D (вход данных): определяет новое значение выхода
• Работа
D Latch
– Когда CLK = 1, D проходит
Symbol
на выход Q (защелка прозрачна)
CLK
– Когда CLK = 0, Q хранит
D Q
предыдущее значение
Q
(защелка непрозрачна)
• Запрещенное состояние не возникает, когда
Q ≠ NOT Q
Глава 3 <15>

16.

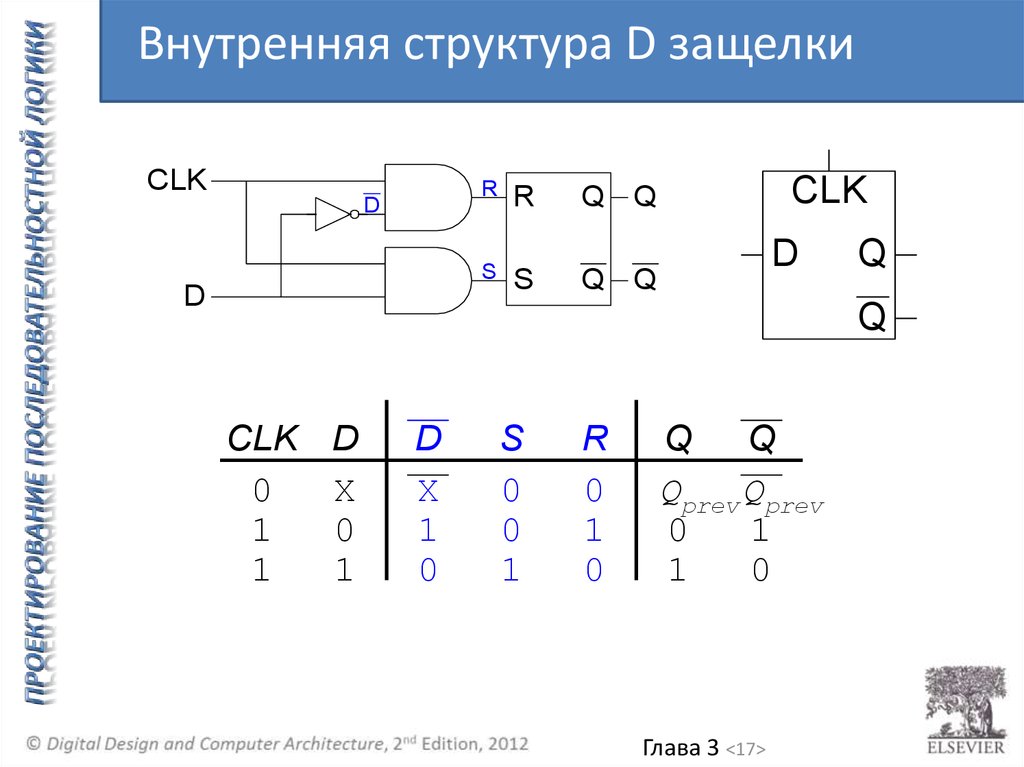
Внутренняя структура D защелки
CLK
R
D
S
D
R
S
CLK
Q Q
D
Q Q
Q
Q
CLK D
0
X
1
0
1
1
D
S
R
Q
Q
Глава 3 <16>

17.

Внутренняя структура D защелки
CLK
R
D
S
D
R
S
CLK
Q Q
D
Q Q
Q
Q
CLK D
0
X
1
0
1
1
D
X
1
0
S
0
0
1
R
0
1
0
Q
Q
Qprev Qprev
0
1
1
0
Глава 3 <17>

18.

D-триггер
• Входы: CLK, D
• Работа
D Flip-Flop
Symbols
– Фиксирует значение D по переднему
фронту CLK
D
• Когда CLK изменяется от 0 к 1, D
проходит на выход Q
• В противном случае Q хранит
предыдущее значение
– Q изменяется только по переднему
фронту CLK
• Такой триггер управляется фронтом
• Активируется фронтом тактового сигнала
Глава 3 <18>
Q
Q

19.

Внутренняя структура D триггера
• Две последовательно соединенные защелки (L1 и L2), которые
управляются комплементарными тактовыми сигналами
• Когда CLK = 0
– L1 прозрачна
– L2 непрозрачна
– D проходит до N1
• Когда CLK = 1
– L2 прозрачна
– L1 непрозрачна
– N1 проходит до Q
CLK
CLK
D D
L1
Q
Q
CLK
N1
D
Q Q
L2
Q Q
• Следовательно, по фронту тактового сигнала (когда CLK
меняется от 0 к 1)
– D проходит до Q
Глава 3 <19>

20.

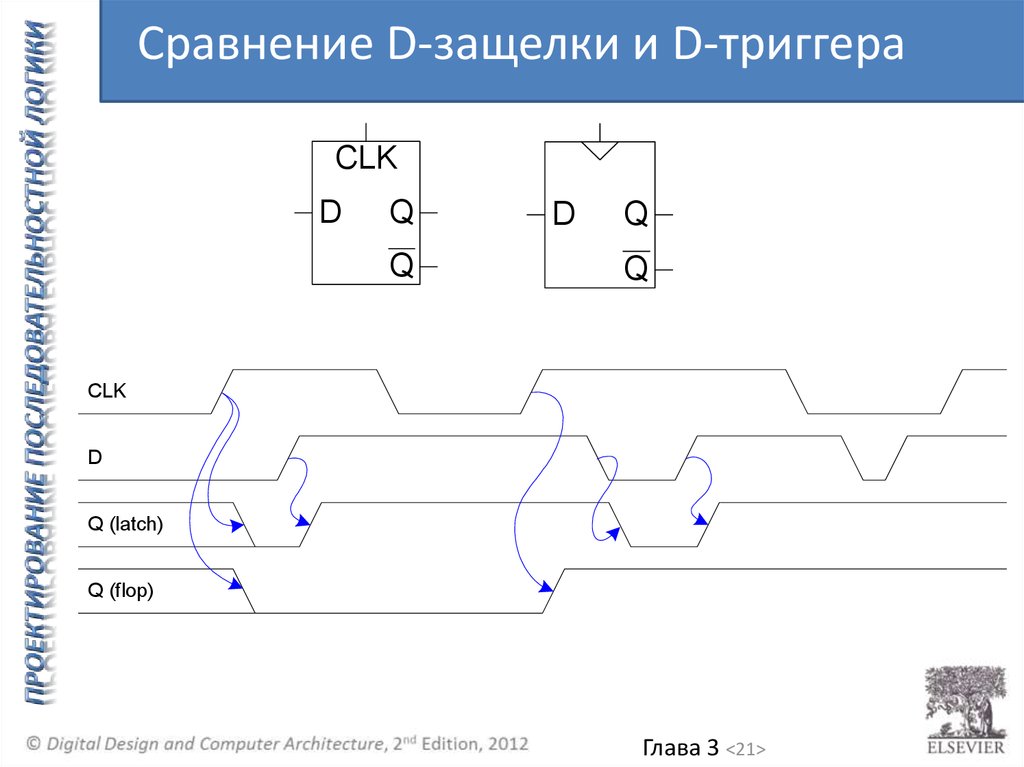
Сравнение D-защелки и D-триггера
CLK
D
Q
Q
D
Q
Q
CLK
D
Q (latch)
Q (flop)
Глава 3 <20>

21.

Сравнение D-защелки и D-триггера
CLK
D
Q
Q
D
Q
Q
CLK
D
Q (latch)
Q (flop)
Глава 3 <21>

22.

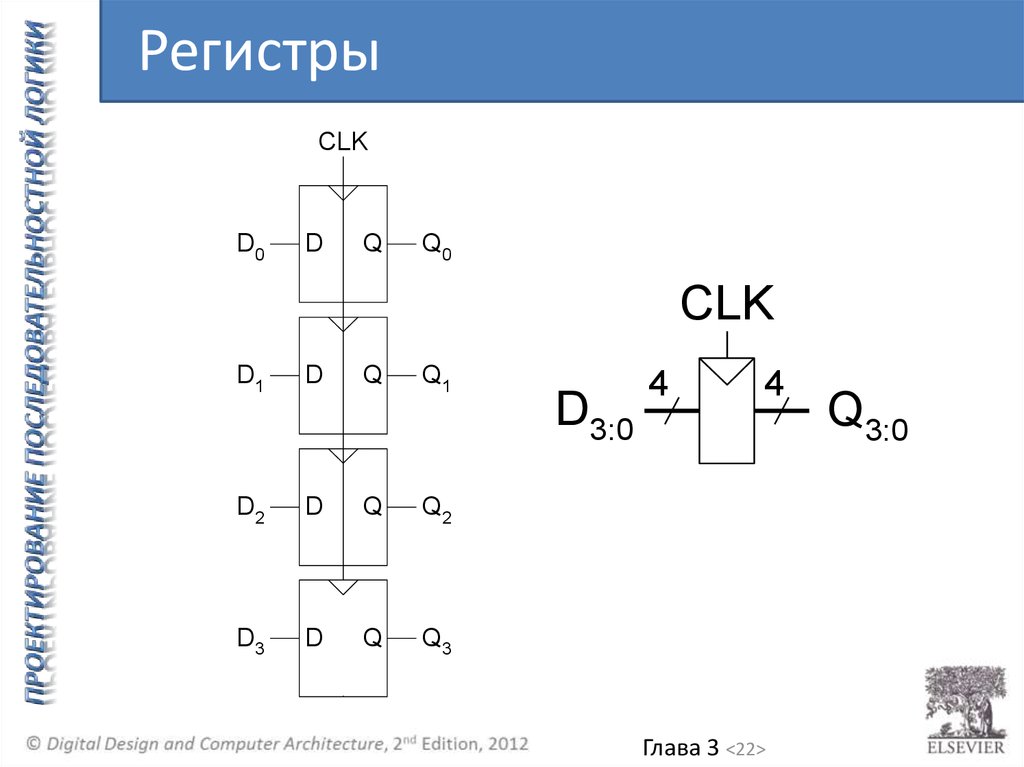
Регистры
CLK
D0
D
Q
Q0
CLK
D1
D
Q
Q1
D2
D
Q
Q2
D3
D
Q
Q3
D3:0
4
4
Глава 3 <22>
Q3:0

23.

D-триггер с функцией разрешения
• Входы: CLK, D, EN
– Вход разрешения (EN) контролирует, будут ли
сохраняться новые данные (D)
• Работа
– EN = 1: D проходит на Q по фронту тактового сигнала
– EN = 0: триггер сохраняет предыдущее состояние
Internal
Circuit
EN
Symbol
CLK
0
D
D
1
Q
Q
D
Q
EN
Глава 3 <23>

24.

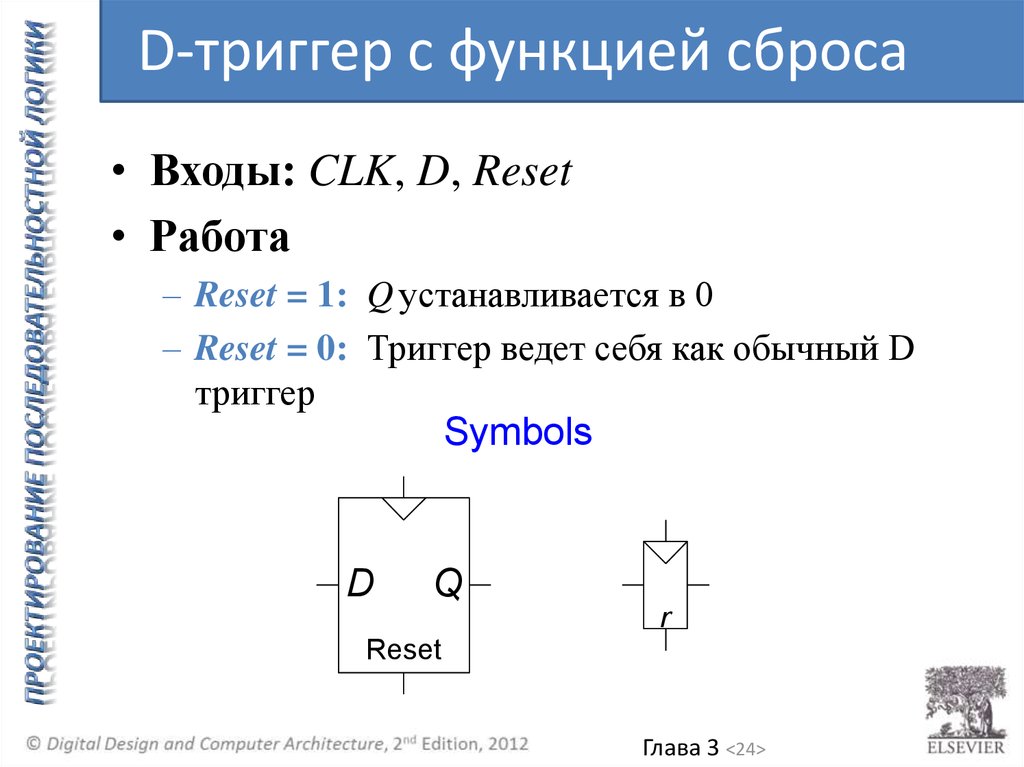
D-триггер с функцией сброса
• Входы: CLK, D, Reset
• Работа
– Reset = 1: Q устанавливается в 0
– Reset = 0: Триггер ведет себя как обычный D
триггер
Symbols
D
Q
r
Reset
Глава 3 <24>

25.

D-триггер с функцией сброса
• Два типа:
– Синхронный: Сброс происходит только по
фронту тактового сигнала
– Асинхронный: сброс происходит сразу после
установки Reset в 1
• Асинхронно сбрасываемые триггеры
требуют отличаются от обычных
внутренней структурой
• Триггер с функцией синхронного сброса?
Глава 3 <25>

26.

Триггеры с функцией сброса
• Два типа:
– Синхронный: Сброс происходит только по фронту
тактового сигнала
– Асинхронный: сброс происходит сразу после
установки Reset в 1
• Асинхронно сбрасываемые триггеры требуют
отличаются от обычных внутренней структурой
• Триггер с функцией синхронного сброса?
Internal
Circuit
CLK
D
Reset
D
Q
Q
Глава 3 <26>

27.

Триггеры с функцией установки
• Входы: CLK, D, Set
• Работа:
– Set = 1: Q устанавливается в 1
– Set = 0: Триггер ведет себя как обычный D
триггер
Symbols
D
Q
s
Set
Глава 3 <27>

28.

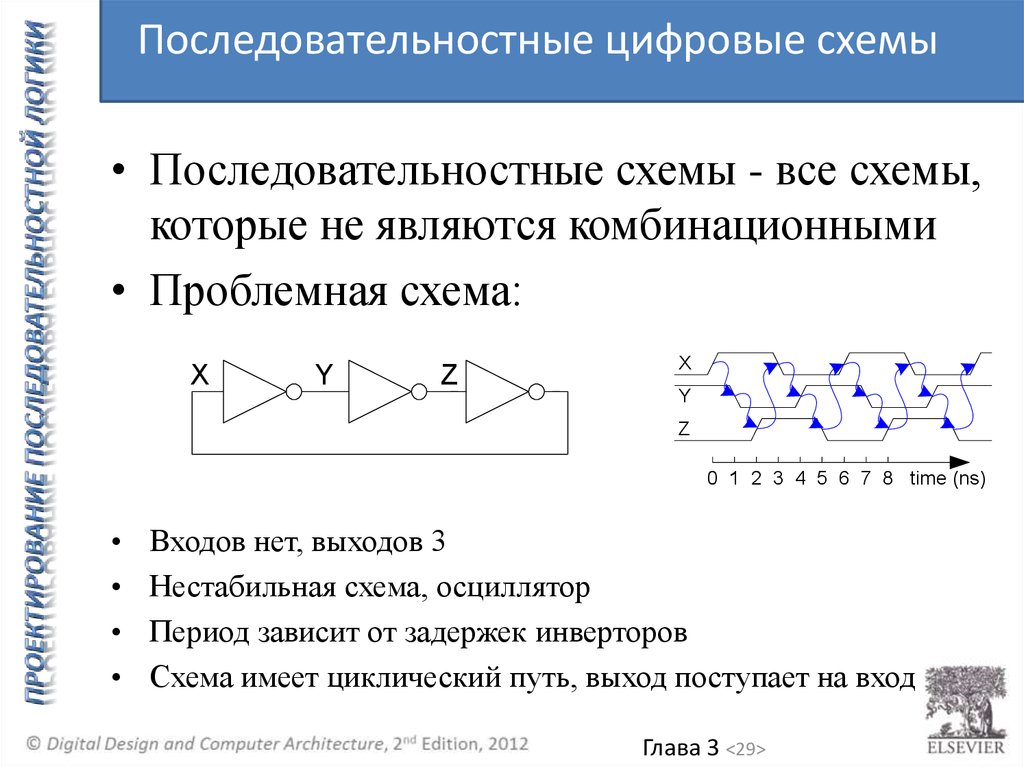
Последовательностные цифровые схемы
• Последовательностные схемы - все схемы,
которые не являются комбинационными
• Проблемная схема:
X
Y
Z
X
Y
Z
0 1 2 3 4 5 6 7 8 time (ns)
Глава 3 <28>

29.

Последовательностные цифровые схемы
• Последовательностные схемы - все схемы,
которые не являются комбинационными
• Проблемная схема:
X
Y
Z
X
Y
Z
0 1 2 3 4 5 6 7 8 time (ns)
Входов нет, выходов 3
Нестабильная схема, осциллятор
Период зависит от задержек инверторов
Схема имеет циклический путь, выход поступает на вход
Глава 3 <29>

30.

Проектирование синхронных логических схем
• Разрушение циклических путей с путем добавления регистров
• Регистры сохраняет состояние схемы
• Состояние изменяется по фронтам тактового сигнала, система
синхронизируется этим сигналом
• Правила построения синхронных последовательностных схем:
– Каждый элемент схемы является либо регистром, либо
комбинационной схемой
– Как минимум один элемент схемы является регистром
– Все регистры тактируются единственным тактовым сигналом
– В каждом циклическом пути присутствует как минимум один
регистр
• Два основные типа синхронных последовательностных схем
– Конечные автоматы (FSM)
– Конвейеры
Глава 3 <30>

31.

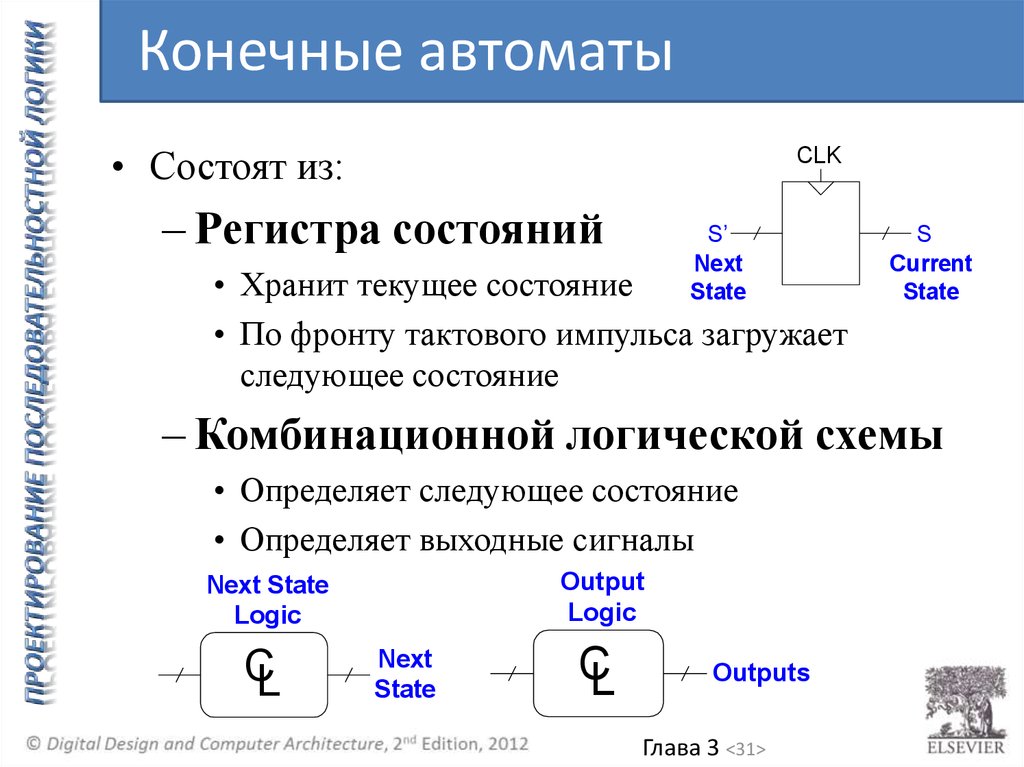
Конечные автоматы
• Состоят из:
CLK
– Регистра состояний
S’
Next
State
• Хранит текущее состояние
• По фронту тактового импульса загружает
следующее состояние
S
Current
State
– Комбинационной логической схемы
• Определяет следующее состояние
• Определяет выходные сигналы
Output
Logic
Next State
Logic
CL
Next
State
CL
Outputs
Глава 3 <31>

32.

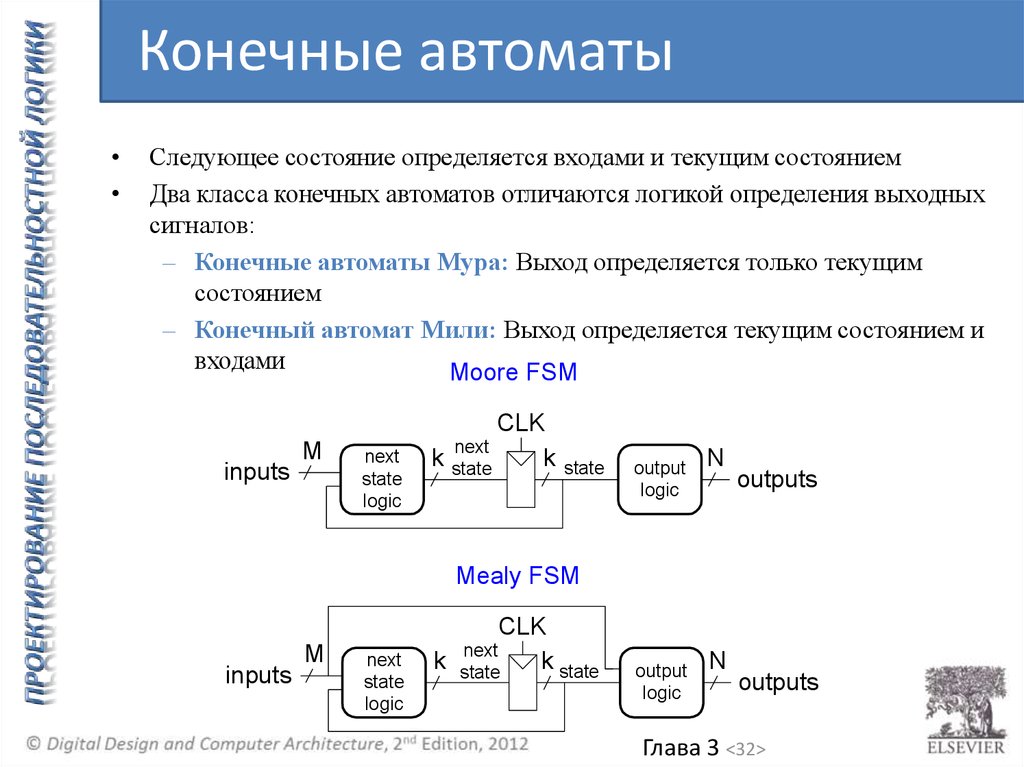
Конечные автоматы
Следующее состояние определяется входами и текущим состоянием
Два класса конечных автоматов отличаются логикой определения выходных
сигналов:
– Конечные автоматы Мура: Выход определяется только текущим
состоянием
– Конечный автомат Мили: Выход определяется текущим состоянием и
входами
Moore FSM
inputs
M
next
state
logic
CLK
next
k state
k
state
output
logic
N
outputs
Mealy FSM
inputs
M
next
state
logic
CLK
next
k state
k state
output
logic
N
outputs
Глава 3 <32>

33.

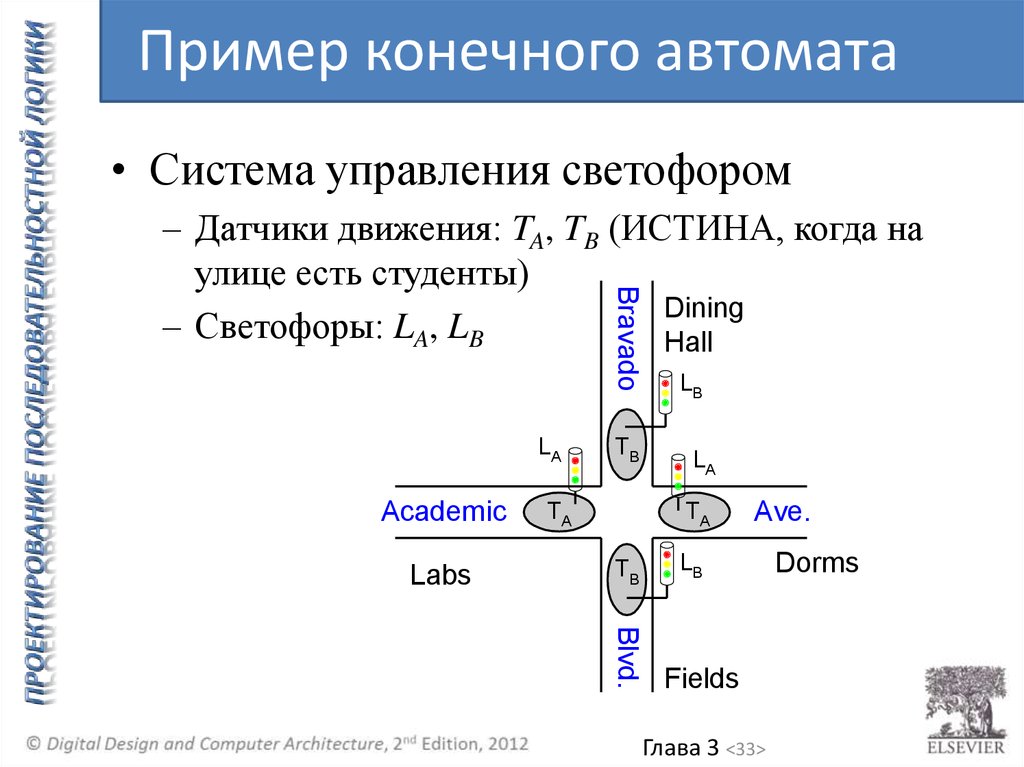
Пример конечного автомата
• Система управления светофором
Bravado
– Датчики движения: TA, TB (ИСТИНА, когда на
улице есть студенты)
Dining
– Светофоры: LA, LB
Hall
LA
Academic
Labs
TB
TA
LB
LA
TA
TB
Ave.
LB
Blvd.
Fields
Глава 3 <33>
Dorms

34.

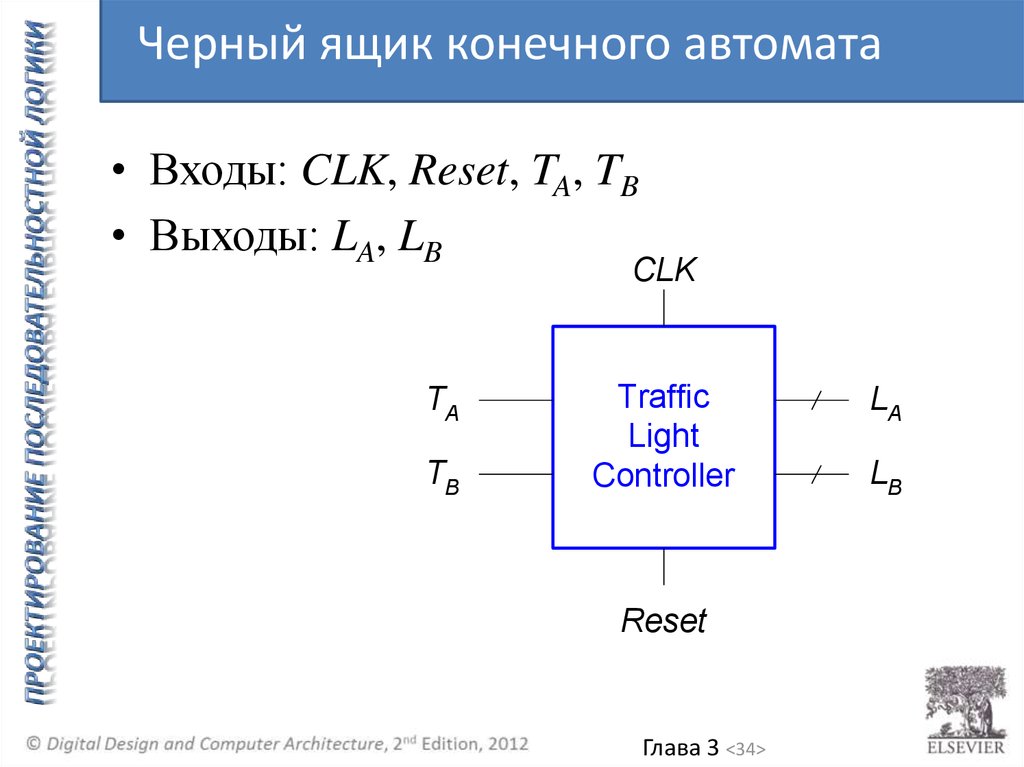
Черный ящик конечного автомата
• Входы: CLK, Reset, TA, TB
• Выходы: LA, LB
CLK
TA
TB
Traffic
Light
Controller
Reset
Глава 3 <34>
LA
LB

35.

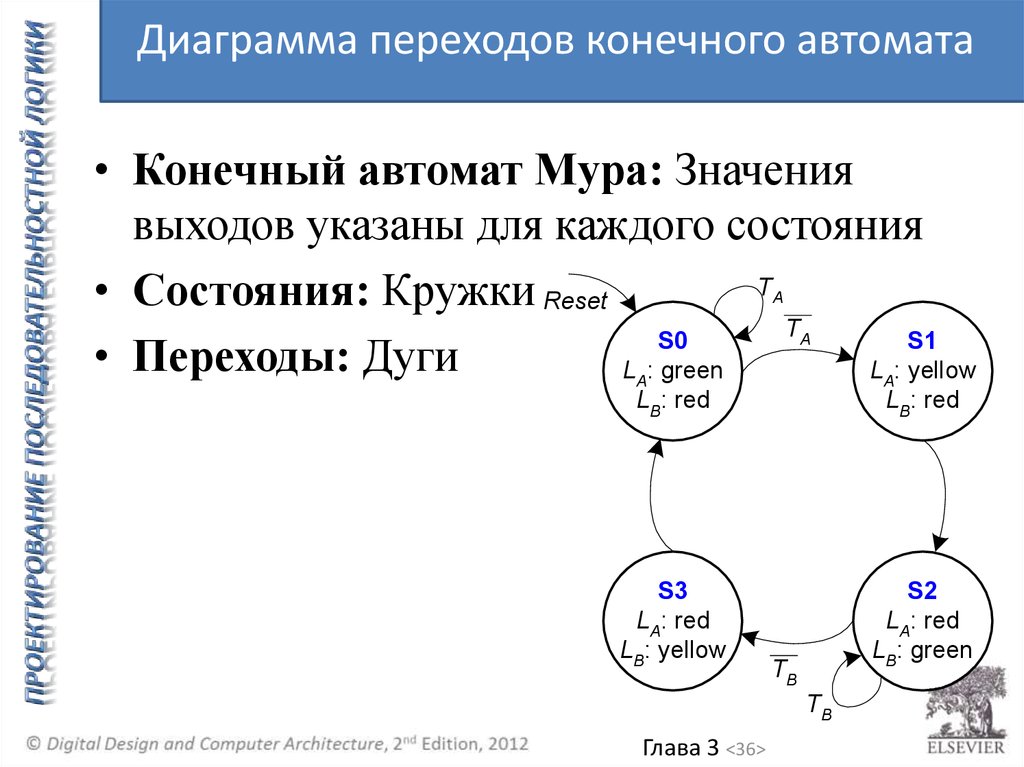
Диаграмма переходов конечного автомата
• Конечный автомат Мура: Значения
выходов указаны для каждого состояния
• Состояния: Кружки
Reset
S0
• Переходы: Дуги
L : green
A
LB: red
Глава 3 <35>

36.

Диаграмма переходов конечного автомата
• Конечный автомат Мура: Значения
выходов указаны для каждого состояния
T
• Состояния: Кружки Reset
T
S0
S1
• Переходы: Дуги
L : green
L : yellow
A
A
A
A
LB: red
S3
LA: red
LB: yellow
LB: red
S2
LA: red
LB: green
TB
TB
Глава 3 <36>

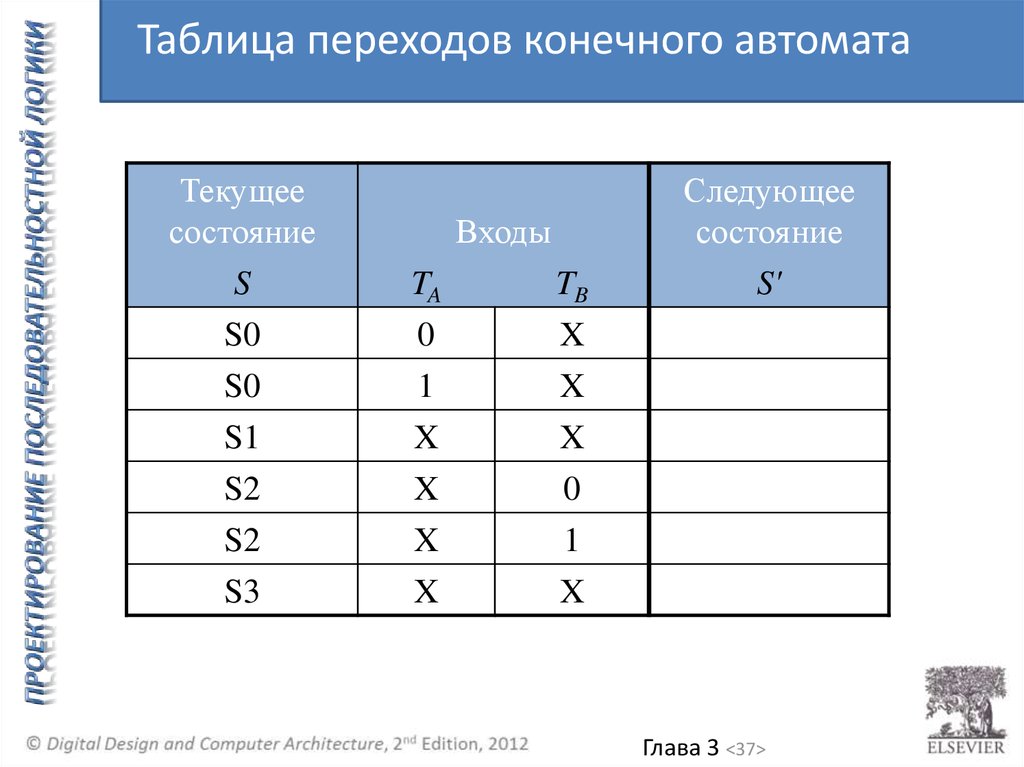
37.

Таблица переходов конечного автомата
Текущее
состояние
Следующее
состояние
Входы
S
S0
S0
TA
0
1
TB
X
X
S1
S2
S2
X
X
X
X
0
1
S3
X
X
S'
Глава 3 <37>

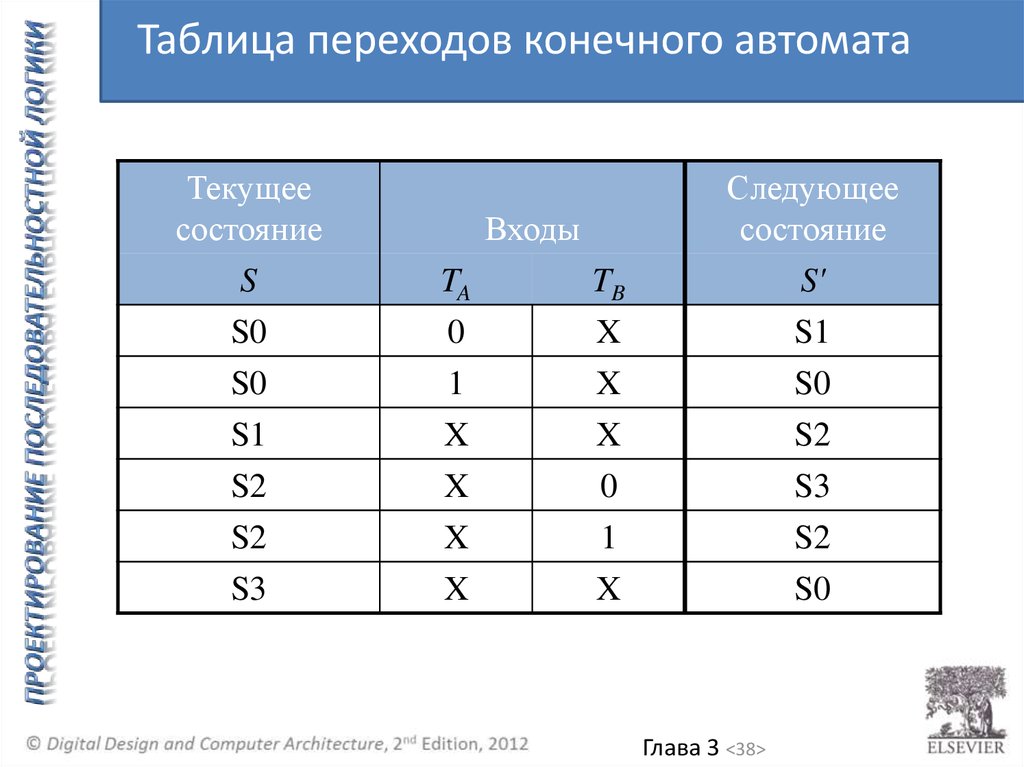
38.

Таблица переходов конечного автомата
Текущее
состояние
S
S0
S0
S1
S2
S2
S3
Входы
TA
0
TB
X
1
X
X
X
X
0
X
X
1
X
Следующее
состояние
S'
S1
S0
S2
S3
S2
S0
Глава 3 <38>

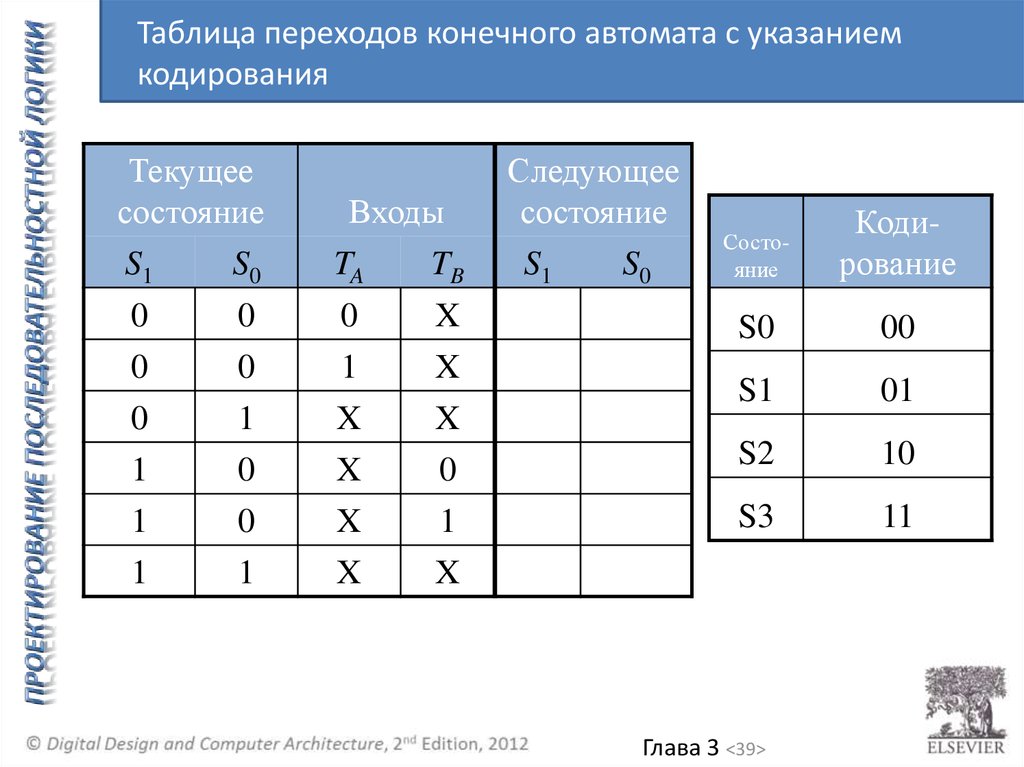
39.

Таблица переходов конечного автомата с указанием
кодирования
Текущее
состояние
S1
S0
Входы
TA
TB
Следующее
состояние
S1
S0
Состояние
Кодирование
0
0
0
0
0
1
0
1
X
X
X
X
S0
00
S1
01
1
1
0
0
X
X
0
1
S2
10
S3
11
1
1
X
X
Глава 3 <39>

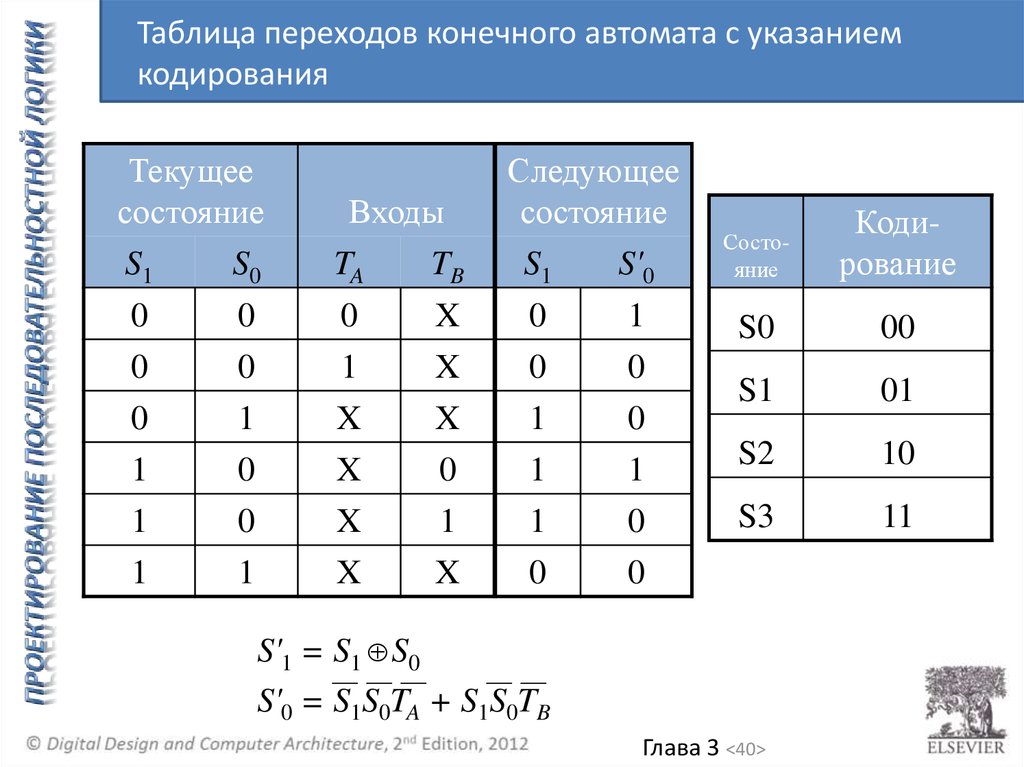
40.

Таблица переходов конечного автомата с указанием
кодирования
Текущее
состояние
S1
S0
Входы
TA
TB
Следующее
состояние
S1
S'0
Состояние
Кодирование
0
0
0
0
0
1
0
1
X
X
X
X
0
0
1
1
0
0
S0
00
S1
01
1
1
0
0
X
X
0
1
1
1
1
0
S2
10
S3
11
1
1
X
X
0
0
S'1 = S1 S0
S'0 = S1S0TA + S1S0TB
Глава 3 <40>

41.

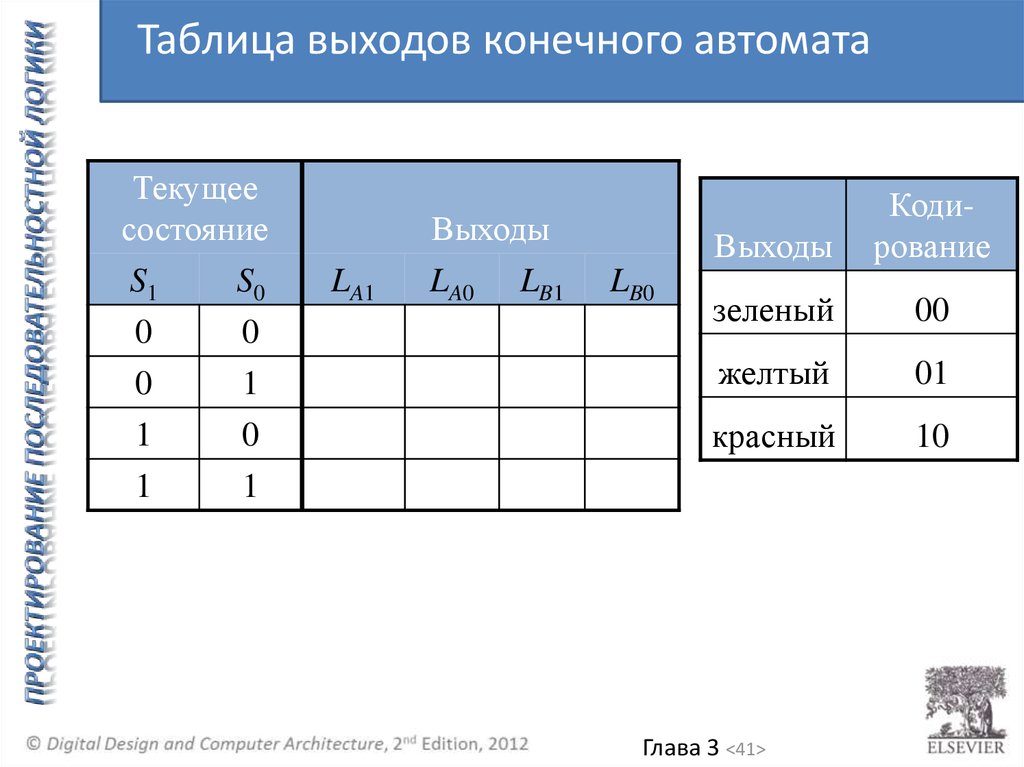
Таблица выходов конечного автомата
Текущее
состояние
S1
S0
0
0
0
1
1
0
1
1
LA1
Выходы
LA0 LB1
LB0
Выходы
Кодирование
зеленый
00
желтый
01
красный
10
Глава 3 <41>

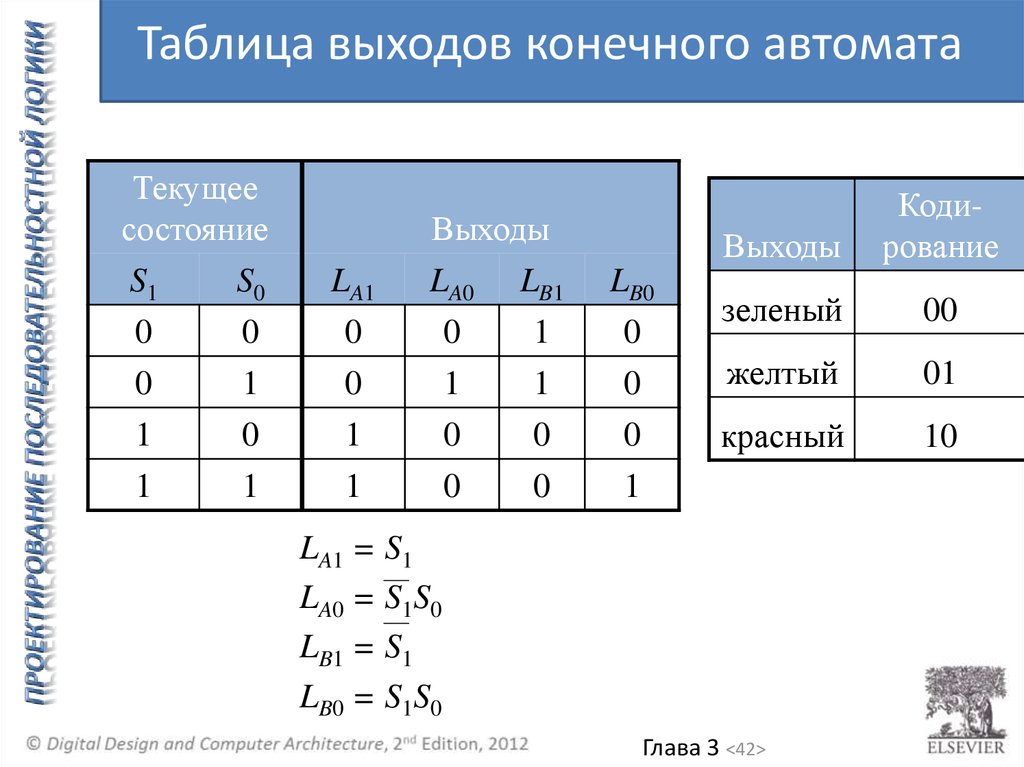
42.

Таблица выходов конечного автомата
Текущее
состояние
S1
S0
0
0
0
1
1
0
1
1
LA1
0
Выходы
LA0 LB1
0
1
0
1
1
1
0
0
1
0
0
LB0
0
0
0
1
Выходы
Кодирование
зеленый
00
желтый
01
красный
10
LA1 = S1
LA0 = S1S0
LB1 = S1
LB0 = S1S0
Глава 3 <42>

43.

Схема конечного автомата: Регистр состояний
CLK
S'1
S1
S'0
S0
r
Reset
state register
Глава 3 <43>

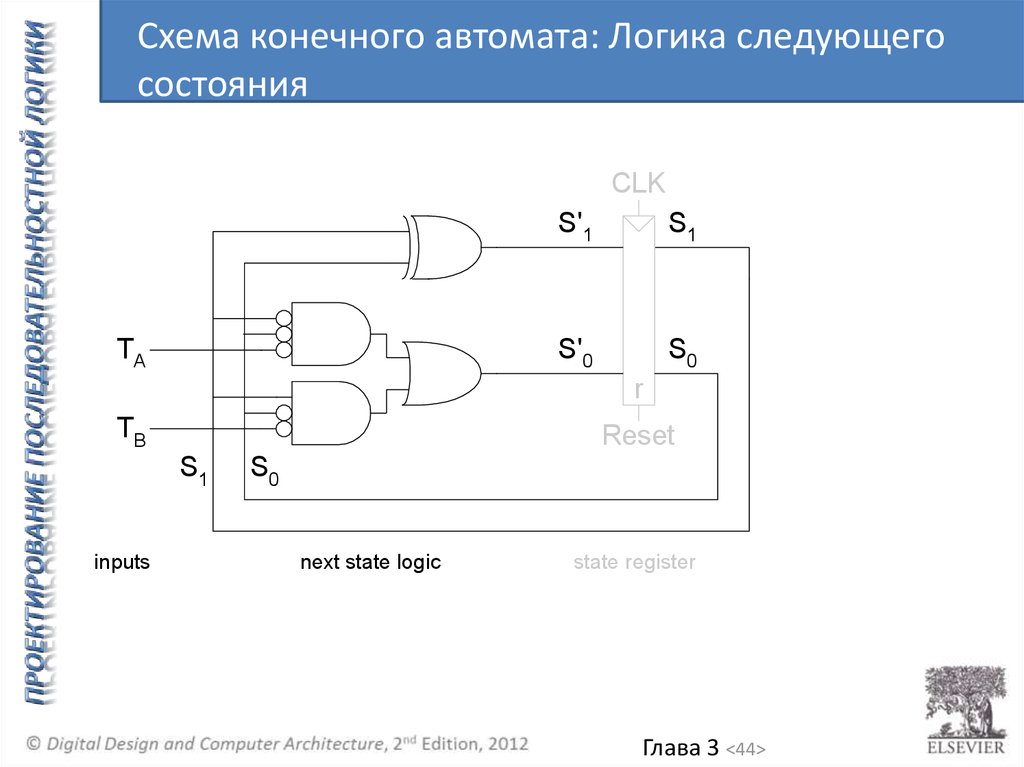
44.

Схема конечного автомата: Логика следующего
состояния
CLK
TA
S'1
S1
S'0
S0
r
TB
Reset
S1
inputs
S0
next state logic
state register
Глава 3 <44>

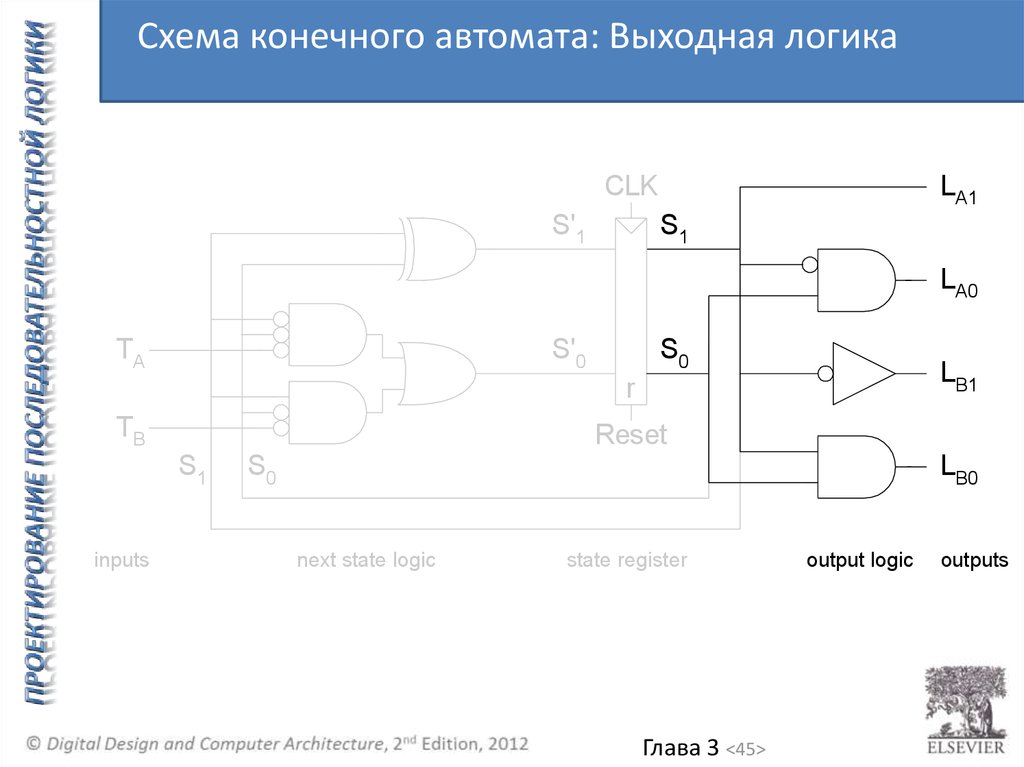
45.

Схема конечного автомата: Выходная логика
CLK
S'1
LA1
S1
LA0
TA
S'0
S0
LB1
r
TB
Reset
S1
inputs
S0
LB0
next state logic
state register
Глава 3 <45>
output logic
outputs

46.

Временная диаграмма конечного автомата
Cycle 1
Cycle 2
Cycle 3
Cycle 4
Cycle 5
Cycle 6
Cycle 7
Cycle 8
Cycle 9
Cycle 10
CLK
Reset
TA
TB
S'1:0
??
S1:0
??
S0 (00)
S1
LA1:0
??
Green (00)
Yellow (01)
LB1:0
??
Red (10)
0
S0 (00)
5
S1 (01)
S2
S3
(10)
(11)
S2 (10)
(01)
S3 (11)
Red (10)
15
20
25
30
S0
LA: green
LB: red
S3
LA: red
LB: yellow
TA
35
S1
LA: yellow
LB: red
S2
LA: red
LB: green
TB
(01)
S0 (00)
Yellow (01) Red (10)
TA
Reset
S1
Green (00)
Green (00)
10
S0 (00)
TB
Глава 3 <46>
40
45
t (sec)

47.

Кодирование состояний конечного автомата
• Двоичное кодирование:
– Для четырех состояний: 00, 01, 10, 11
• Прямое (One-hot) кодирование
–
–
–
–
–
На каждое состояние один бит
Только один бит имеет значение ИСТИНА
Для четырех состояний: 0001, 0010, 0100, 1000
Используется больше триггеров
Часто логика следующего состояния и выходная
логика проще
Глава 3 <47>

48.

Сравнение конечных автоматов Мура и Мили
• У Алисы есть улитка, которая ползает по перфоленте,
содержащей последовательность нулей и единиц. Улитка
улыбается, если последовательность из двух последних
бит, через которые она переползла,
равна 01.
Спроектируйте конечные автоматы
Мура и Мили, определяющие,
когда улитке нужно улыбнуться.
Глава 3 <48>

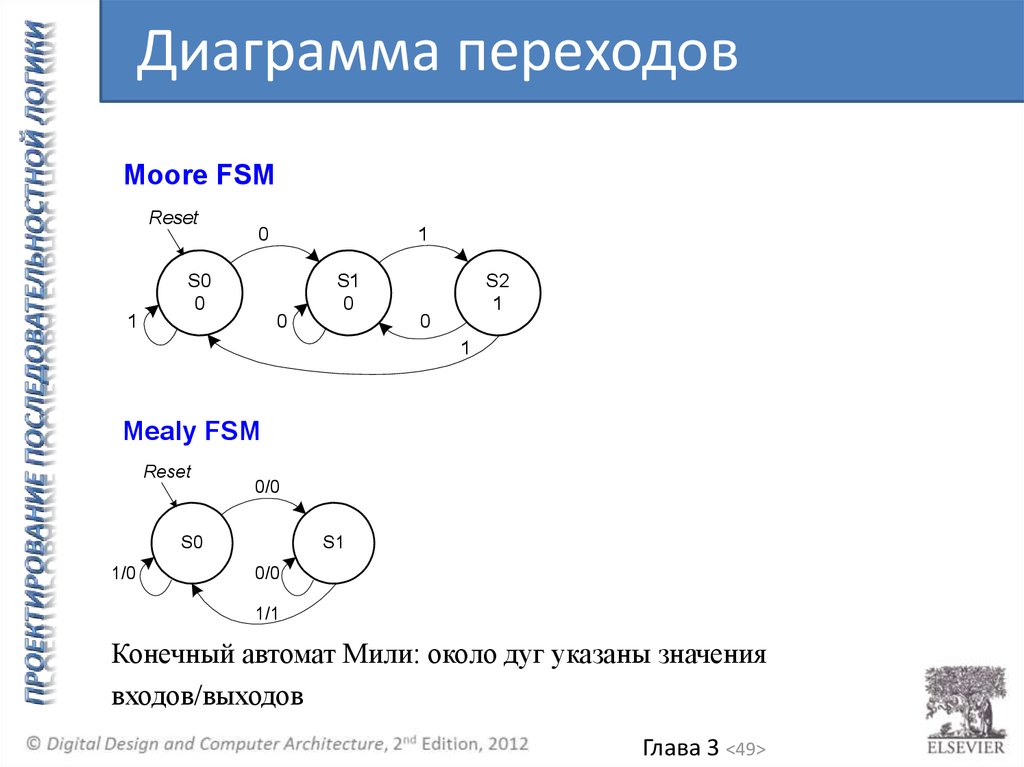
49.

Диаграмма переходов
Moore FSM
Reset
0
1
S0
0
S1
0
1
0
S2
1
0
1
Mealy FSM
Reset
0/0
S0
1/0
S1
0/0
1/1
Конечный автомат Мили: около дуг указаны значения
входов/выходов
Глава 3 <49>

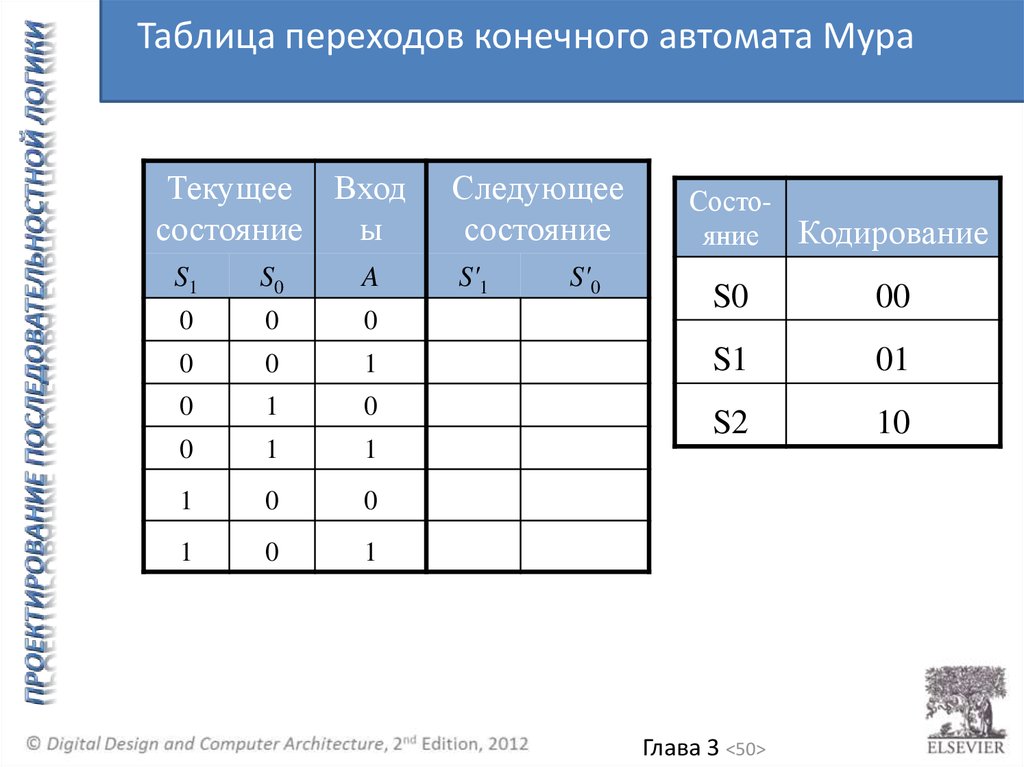
50.

Таблица переходов конечного автомата Мура
Текущее Вход
состояние
ы
S1
S0
A
0
0
0
0
0
0
Следующее
состояние
S'1
S'0
Состояние Кодирование
S0
00
1
S1
01
1
0
0
1
1
S2
10
1
0
0
1
0
1
Глава 3 <50>

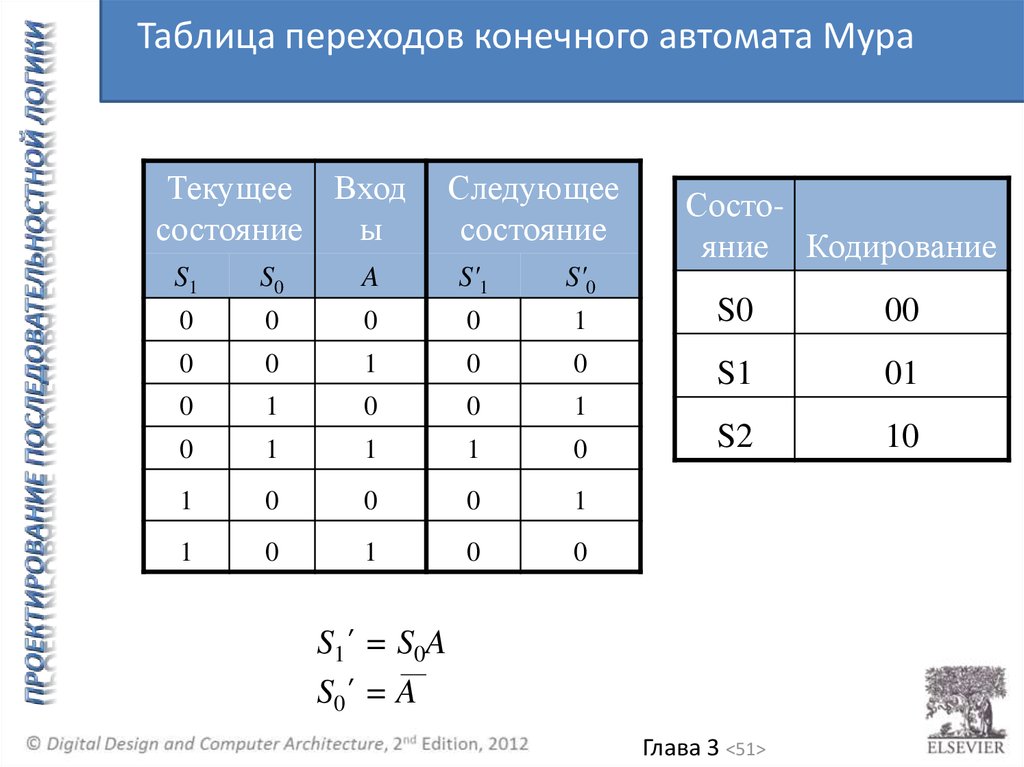
51.

Таблица переходов конечного автомата Мура
Текущее Вход
состояние
ы
Следующее
состояние
Состояние Кодирование
S1
S0
A
S'1
S'0
0
0
0
0
1
S0
00
0
0
1
0
0
S1
01
0
1
0
0
1
0
1
1
1
0
S2
10
1
0
0
0
1
1
0
1
0
0
S1’ = S0A
S0’ = A
Глава 3 <51>

52.

Таблица выходов конечного автомата Мура
Текущее
состояние
S1
S0
0
0
0
1
Выходы
Y
1
0
Y = S1
Глава 3 <52>

53.

Таблица выходов конечного автомата Мура
Текущее
состояние
S1
S0
0
0
0
1
1
0
Выходы
Y
0
0
1
Y = S1
Глава 3 <53>

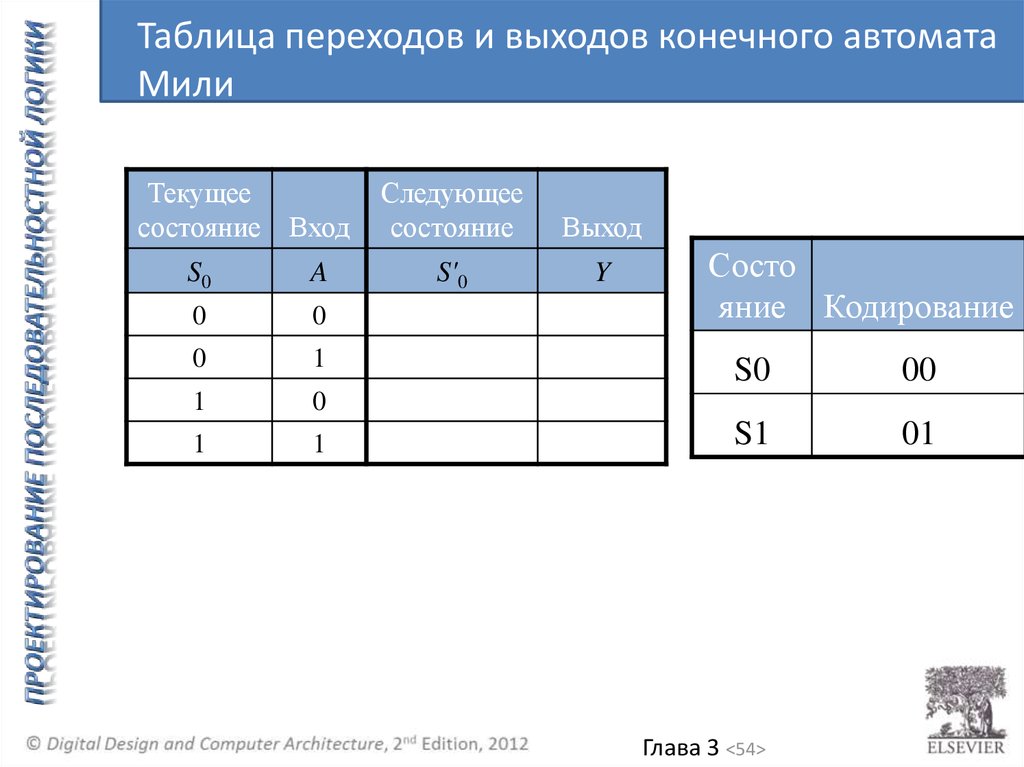
54.

Таблица переходов и выходов конечного автомата
Мили
Текущее
состояние Вход
S0
A
0
0
0
1
1
0
1
1
Следующее
состояние
Выход
S'0
Y
Состо
яние Кодирование
S0
00
S1
01
Глава 3 <54>

55.

Таблица переходов и выходов конечного автомата
Мили
Текущее
состояние Вход
Следующее
состояние
Выход
S0
A
S'0
Y
0
0
1
0
0
1
0
0
1
0
1
0
1
1
0
1
Состояние Кодирование
S0
00
S1
01
Глава 3 <55>

56.

Схема конечного автомата Мура
A
CLK
S'1
S1
S'0
S0
Y
r
Reset
Глава 3 <56>

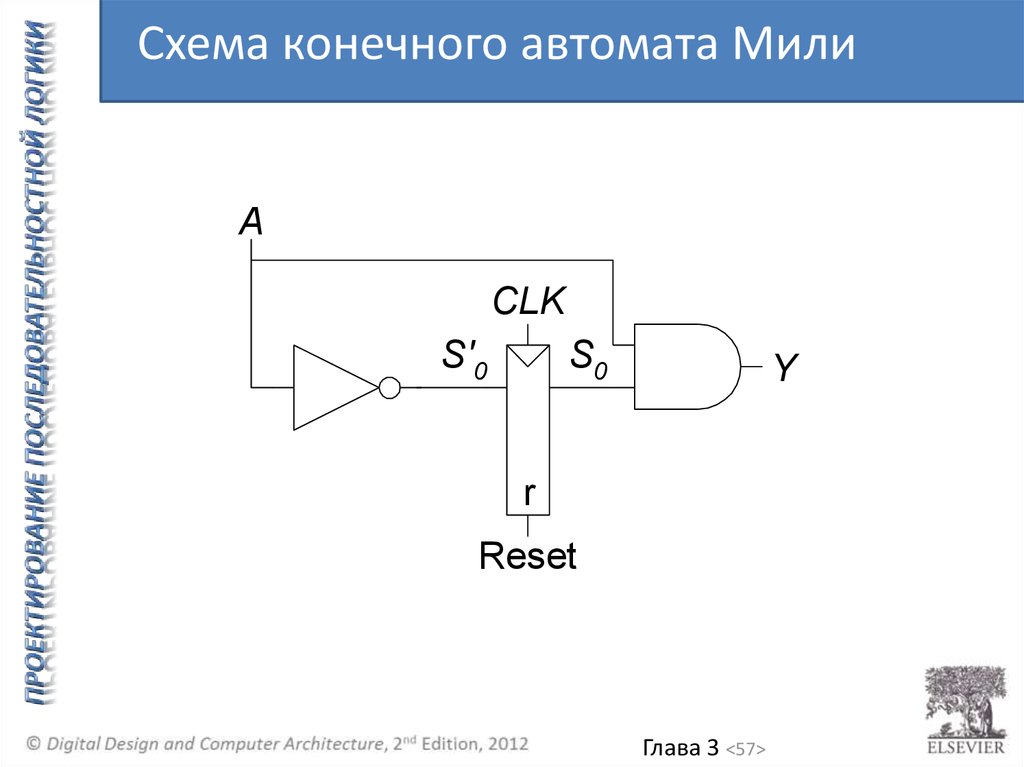
57.

Схема конечного автомата Мили
A
CLK
S'0
S0
Y
r
Reset
Глава 3 <57>

58.

Временные диаграммы конечных автоматов Мура
и Мили
Cycle 1
Cycle 2
Cycle 3
Cycle 4
Cycle 5
Cycle 6
Cycle 7
Cycle 8
Cycle 9 Cycle 10 Cycle 11
CLK
Reset
A
0
1
0
1
1
0
1
1
1
S0
S1
S2
S0
S1
S0
Moore Machine
S ??
S0
S1
S2
S1
S2
Y
Mealy Machine
S ??
S0
S1
S0
S1
S0
Y
Глава 3 <58>

59.

Декомпозиция конечных автоматов
• Разделение сложного конечного автомата на
более простые взаимодействующие конечный
автоматы
• Пример: Модифицируйте контроллер
светофора так, чтобы в нем появился режим
«парада»
– Два дополнительные входа P, R
– Когда P = 1, автомат входит в режим парада и
светофор на Беговой улице остается зеленым
– Когда R = 1, автомат выходит из режима парада
Глава 3 <59>

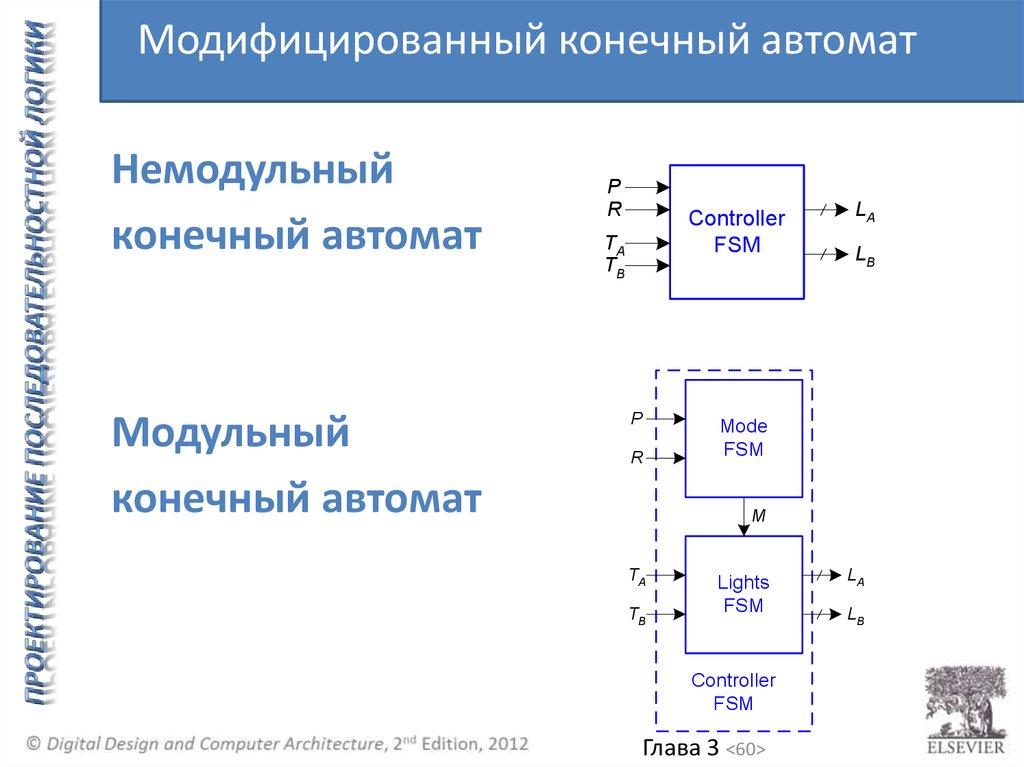
60.

Модифицированный конечный автомат
Немодульный
конечный автомат
Модульный
конечный автомат
P
R
Controller
FSM
TA
TB
P
R
LA
LB
Mode
FSM
M
TA
TB
Lights
FSM
Controller
FSM
Глава 3 <60>
LA
LB

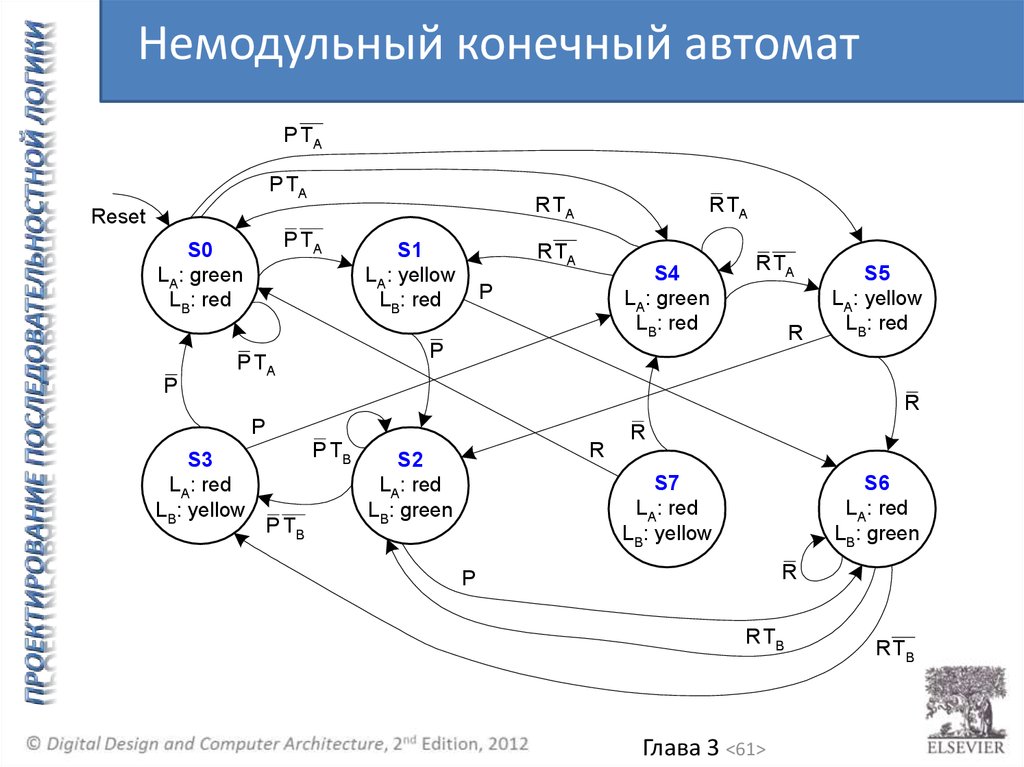
61.

Немодульный конечный автомат
P TA
P TA
R TA
Reset
P TA
S0
LA: green
LB: red
P
S1
LA: yellow
LB: red
R TA
R TA
S4
LA: green
LB: red
P
R
P
P TA
S5
LA: yellow
LB: red
R
P
S3
LA: red
LB: yellow
R TA
P TB
P TB
R
S2
LA: red
LB: green
R
S7
LA: red
LB: yellow
S6
LA: red
LB: green
R
P
R TB
Глава 3 <61>
R TB

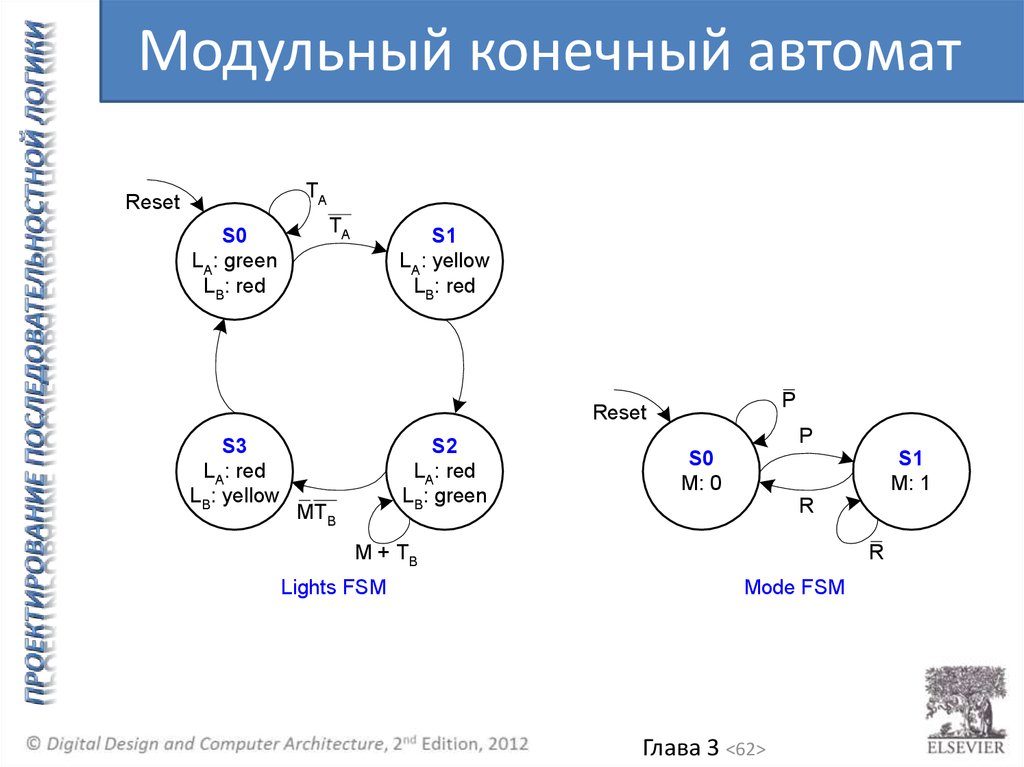
62.

Модульный конечный автомат
TA
Reset
S0
LA: green
LB: red
TA
S1
LA: yellow
LB: red
P
Reset
S3
LA: red
LB: yellow
S2
LA: red
LB: green
MTB
P
S0
M: 0
S1
M: 1
R
M + TB
Lights FSM
R
Mode FSM
Глава 3 <62>

63.

Проектирование конечного автомата
Определите входы и выходы
Нарисуйте диаграмму переходов
Запишите таблицу переходов
Выберите способ кодирования состояний
Для конечного автомата Мура:
– Перепишите таблицу переходов с учетом кодирования
состояний
– Запишите таблицу выходов
Для конечного автомата Мили:
– Перепишите объединенную таблицу переходов и выходов с
учетом кодирования состояний
Запишите булевы выражения логики следующего состояния и
выходов
Нарисуйте принципиальную схему
Глава 3 <63>

64.

Синхронизация
• Триггер фиксирует сигнал D по фронту
тактового сигнала
• Сигнал D должен быть стабильным в
процессе фиксации
• Как при фотографировании, D должен
быть стабильным в окрестности фронта
тактового сигнала
• Если это не так, может возникнуть
метастабильность
Глава 3 <64>

65.

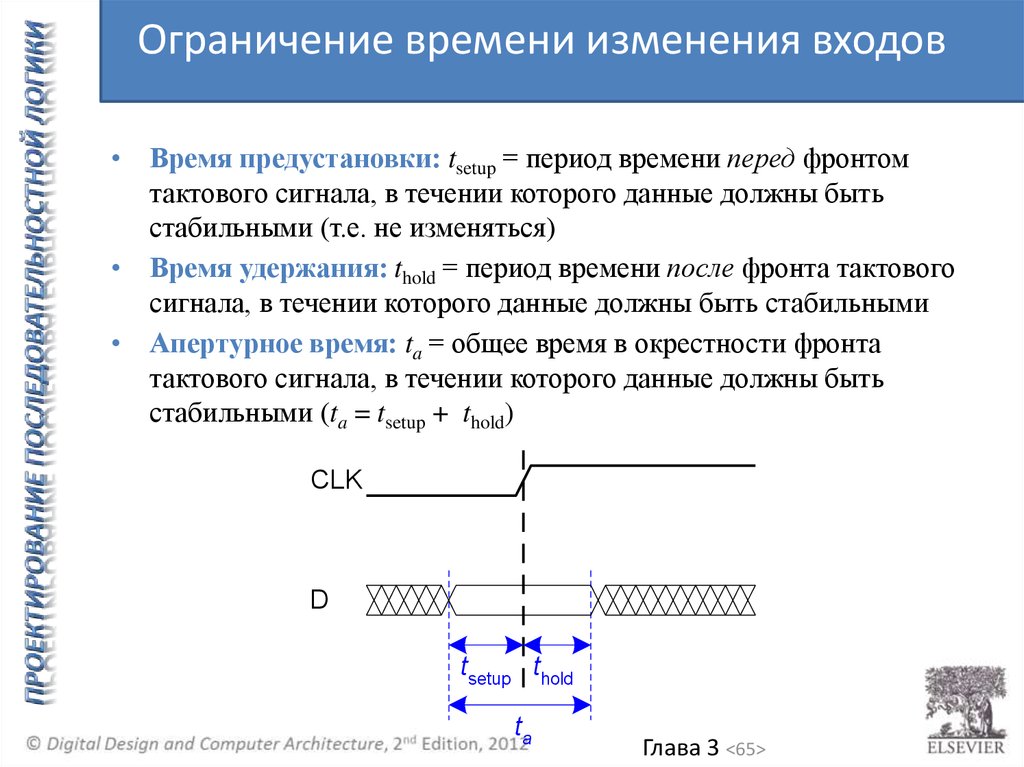
Ограничение времени изменения входов
• Время предустановки: tsetup = период времени перед фронтом
тактового сигнала, в течении которого данные должны быть
стабильными (т.е. не изменяться)
• Время удержания: thold = период времени после фронта тактового
сигнала, в течении которого данные должны быть стабильными
• Апертурное время: ta = общее время в окрестности фронта
тактового сигнала, в течении которого данные должны быть
стабильными (ta = tsetup + thold)
CLK
D
tsetup thold
ta
Глава 3 <65>

66.

Ограничение времени изменения выходов
• Задержка распространения tpcq = период времени после
фронта тактового сигнала, после окончания которого
выход Q будет гарантированно стабильным (т.е,
прекратит изменяться)
• Задержка реакции tccq = период времени после фронта
тактового сигнала, после окончания которого Q может
быть нестабильным (т.е., начать изменяться)
CLK
Q
tccq
tpcq
Глава 3 <66>

67.

Динамическая дисциплина
• Входы синхронной последовательностной
схемы должны быть стабильны в течение
апертурного времени в окрестности
фронта тактового сигнала
• Более точно, входы должны быть
стабильны
– по крайней мере в течении времени tsetup до
фронта тактового импульса
– и по крайней мере в течении времени thold после
фронта тактового импульса
Глава 3 <67>

68.

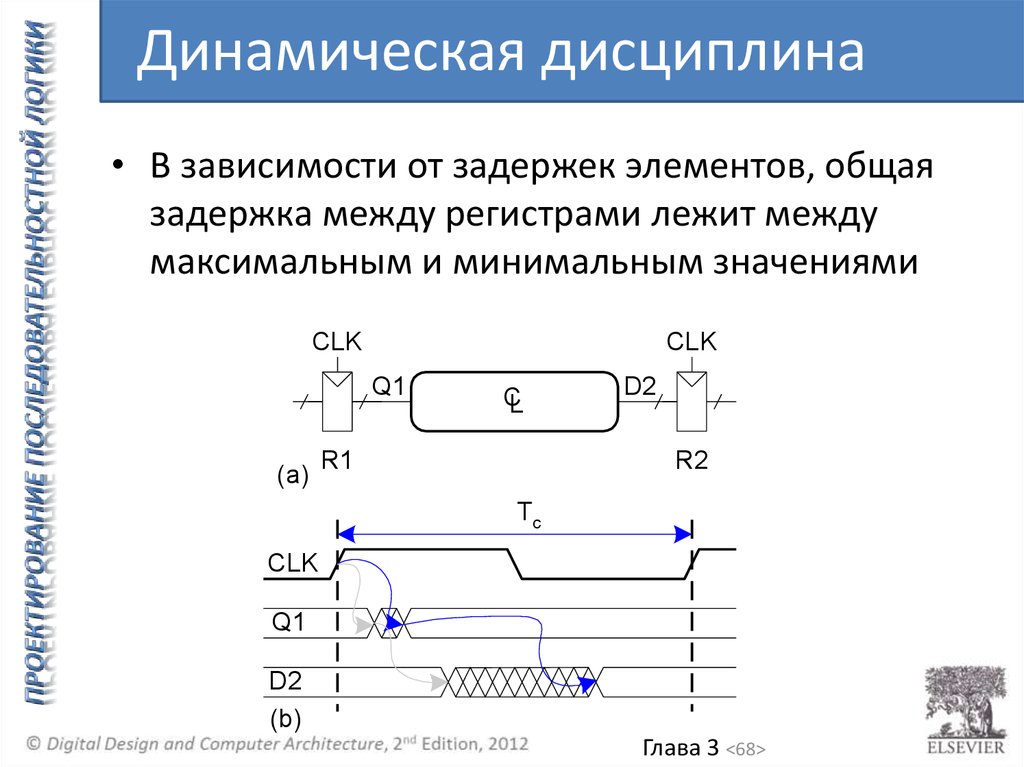
Динамическая дисциплина
• В зависимости от задержек элементов, общая
задержка между регистрами лежит между
максимальным и минимальным значениями
CLK
CLK
Q1
(a)
CL
R1
D2
R2
Tc
CLK
Q1
D2
(b)
Глава 3 <68>

69.

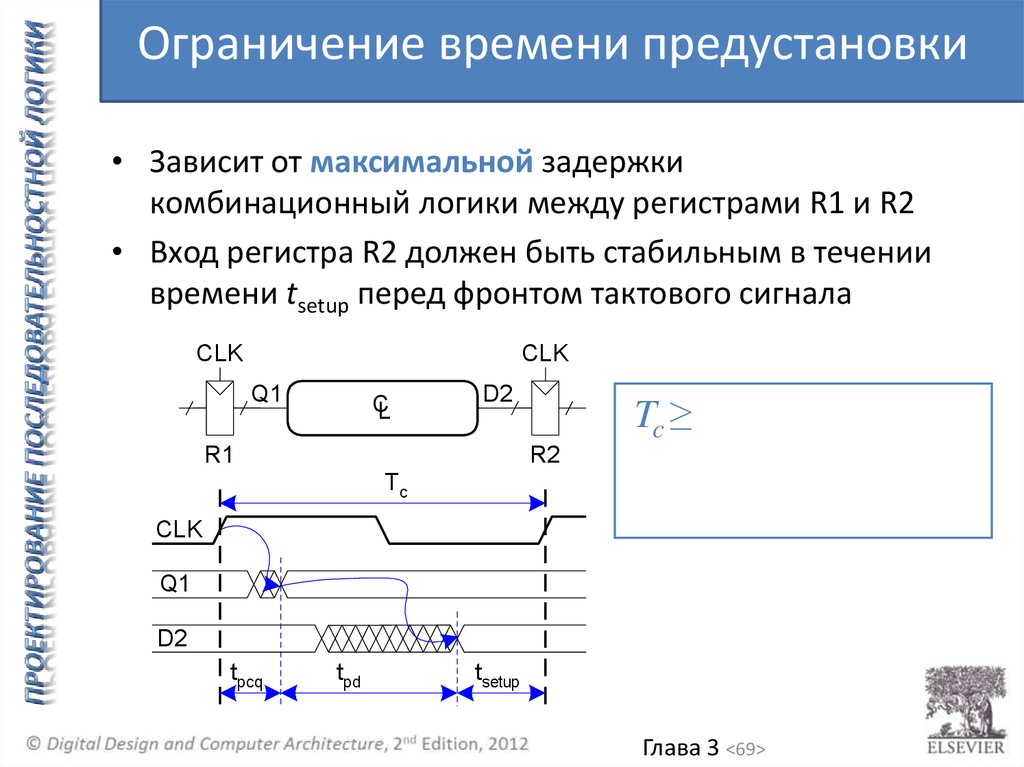
Ограничение времени предустановки
• Зависит от максимальной задержки
комбинационный логики между регистрами R1 и R2
• Вход регистра R2 должен быть стабильным в течении
времени tsetup перед фронтом тактового сигнала
CLK
CLK
Q1
CL
D2
R1
Tc ≥
R2
Tc
CLK
Q1
D2
tpcq
tpd
tsetup
Глава 3 <69>

70.

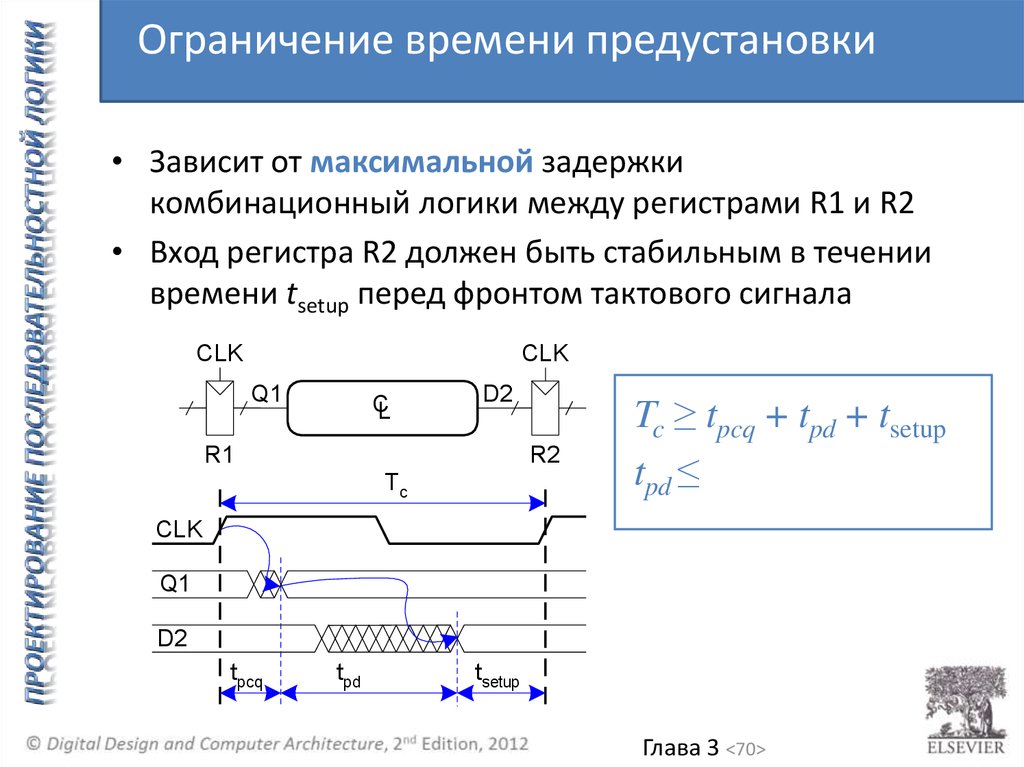
Ограничение времени предустановки
• Зависит от максимальной задержки
комбинационный логики между регистрами R1 и R2
• Вход регистра R2 должен быть стабильным в течении
времени tsetup перед фронтом тактового сигнала
CLK
CLK
Q1
CL
D2
R1
R2
Tc
Tc ≥ tpcq + tpd + tsetup
tpd ≤
CLK
Q1
D2
tpcq
tpd
tsetup
Глава 3 <70>

71.

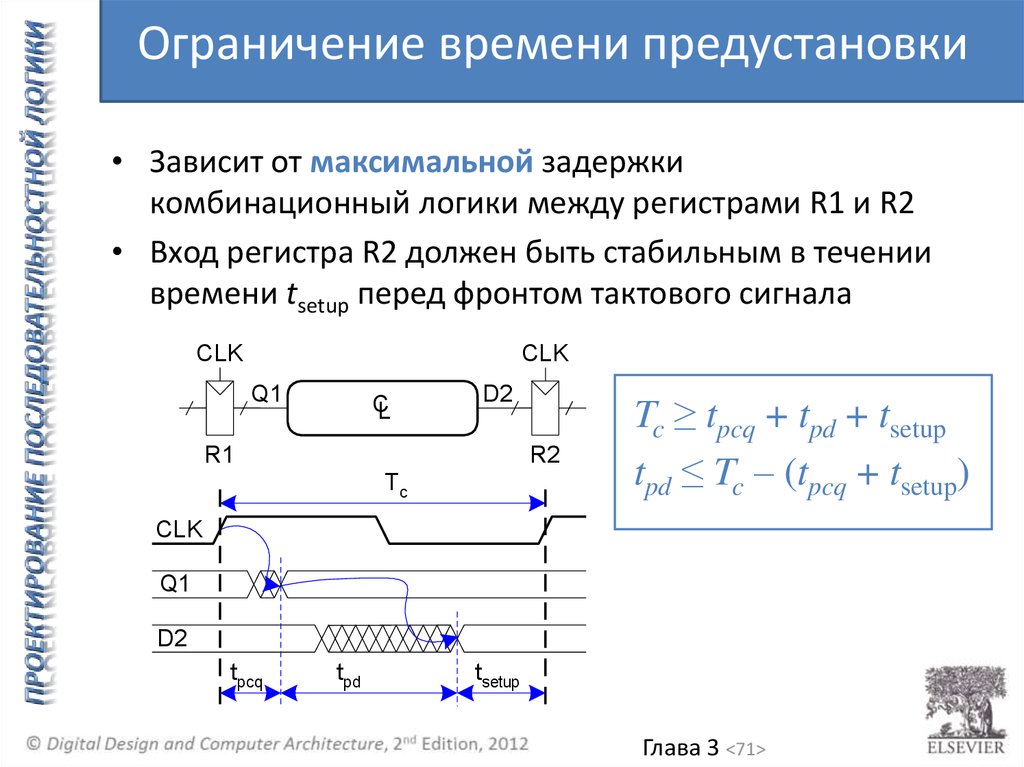
Ограничение времени предустановки
• Зависит от максимальной задержки
комбинационный логики между регистрами R1 и R2
• Вход регистра R2 должен быть стабильным в течении
времени tsetup перед фронтом тактового сигнала
CLK
CLK
Q1
CL
D2
R1
R2
Tc
Tc ≥ tpcq + tpd + tsetup
tpd ≤ Tc – (tpcq + tsetup)
CLK
Q1
D2
tpcq
tpd
tsetup
Глава 3 <71>

72.

Ограничение времени удержания
• Зависит от минимальной задержки
комбинационный логики между регистрами R1 и R2
• Вход регистра R2 должен быть стабильным в течении
времени thold после фронта тактового сигнала
CLK
CLK
Q1
R1
CL
D2
R2
thold <
CLK
Q1
D2
tccq tcd
thold
Глава 3 <72>

73.

Ограничение времени удержания
• Зависит от минимальной задержки
комбинационный логики между регистрами R1 и R2
• Вход регистра R2 должен быть стабильным в течении
времени thold после фронта тактового сигнала
CLK
CLK
Q1
R1
CL
D2
R2
thold < tccq + tcd
tcd >
CLK
Q1
D2
tccq tcd
thold
Глава 3 <73>

74.

Ограничение времени удержания
• Зависит от минимальной задержки
комбинационный логики между регистрами R1 и R2
• Вход регистра R2 должен быть стабильным в течении
времени thold после фронта тактового сигнала
CLK
CLK
Q1
R1
CL
D2
R2
thold < tccq + tcd
tcd > thold - tccq
CLK
Q1
D2
tccq tcd
thold
Глава 3 <74>

75.

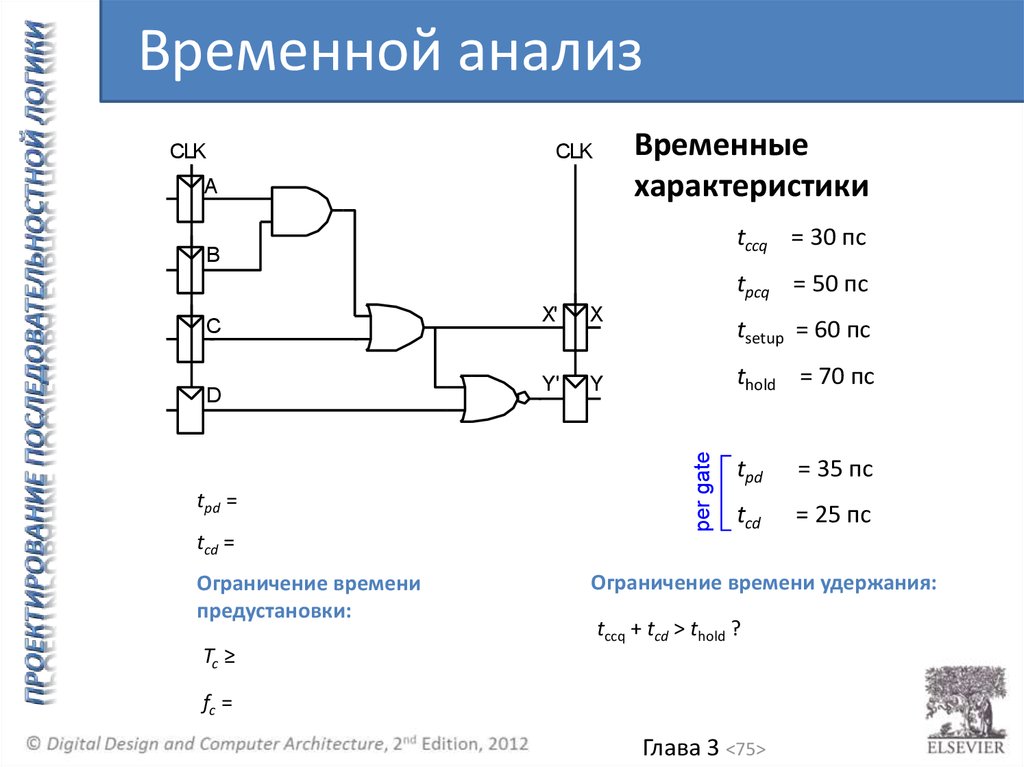
Временной анализ
CLK
Временные
характеристики
CLK
A
tccq = 30 пс
B
tpcq = 50 пс
D
tpd =
tcd =
Ограничение времени
предустановки:
X'
X
Y'
Y
tsetup = 60 пс
thold = 70 пс
per gate
C
tpd
= 35 пс
tcd
= 25 пс
Ограничение времени удержания:
tccq + tcd > thold ?
Tc ≥
fc =
Глава 3 <75>

76.

Временной анализ
CLK
Временные
характеристики
CLK
A
tccq = 30 пс
B
tpcq = 50 пс
D
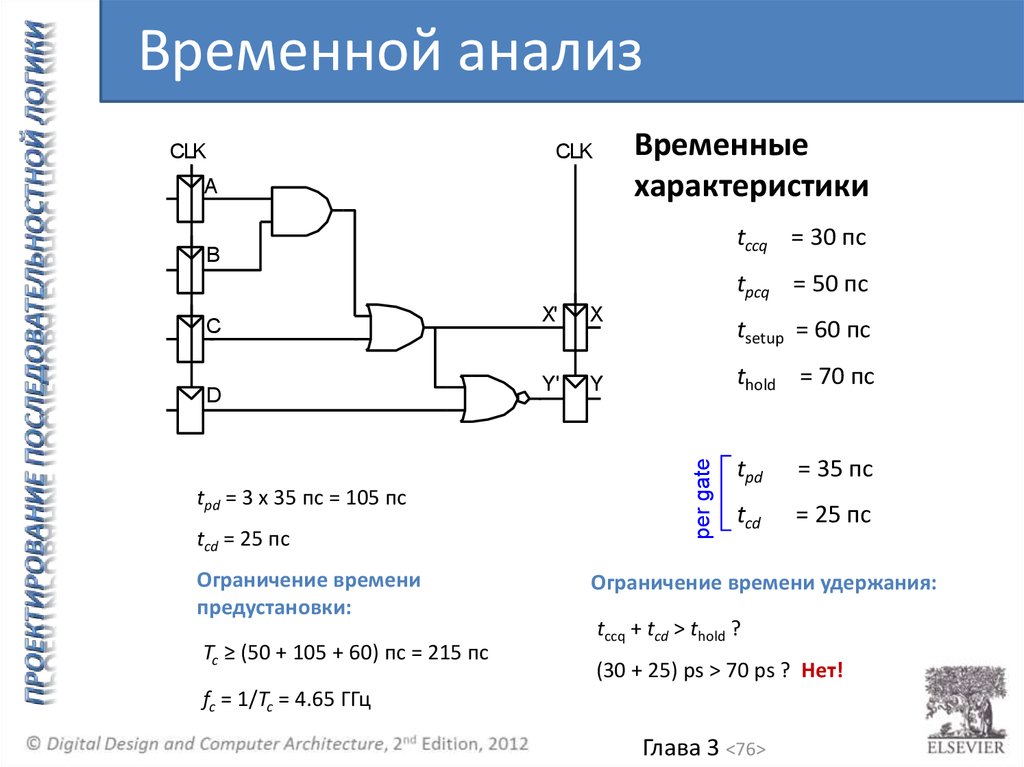
tpd = 3 x 35 пс = 105 пс
tcd = 25 пс
Ограничение времени
предустановки:
Tc ≥ (50 + 105 + 60) пс = 215 пс
X'
X
Y'
Y
tsetup = 60 пс
thold = 70 пс
per gate
C
tpd
= 35 пс
tcd
= 25 пс
Ограничение времени удержания:
tccq + tcd > thold ?
(30 + 25) ps > 70 ps ? Нет!
fc = 1/Tc = 4.65 ГГц
Глава 3 <76>

77.

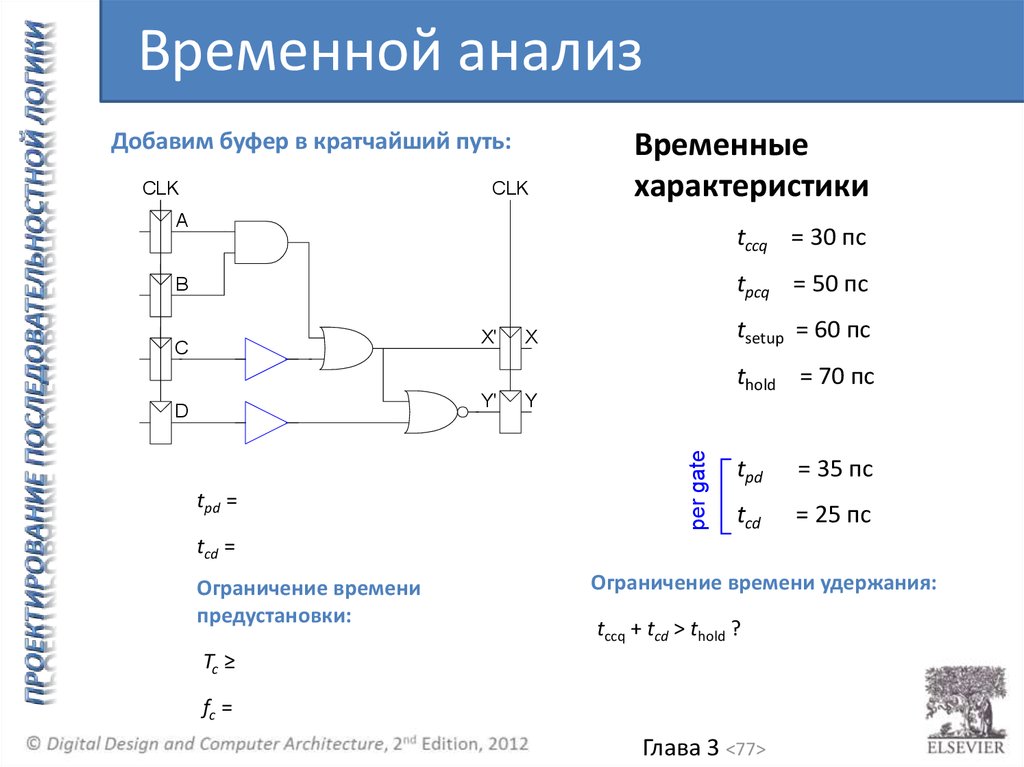
Временной анализ
Добавим буфер в кратчайший путь:
CLK
CLK
Временные
характеристики
A
tccq = 30 пс
tpcq = 50 пс
B
Y'
D
tpd =
tsetup = 60 пс
X
thold = 70 пс
Y
per gate
X'
C
tpd
= 35 пс
tcd
= 25 пс
tcd =
Ограничение времени
предустановки:
Ограничение времени удержания:
tccq + tcd > thold ?
Tc ≥
fc =
Глава 3 <77>

78.

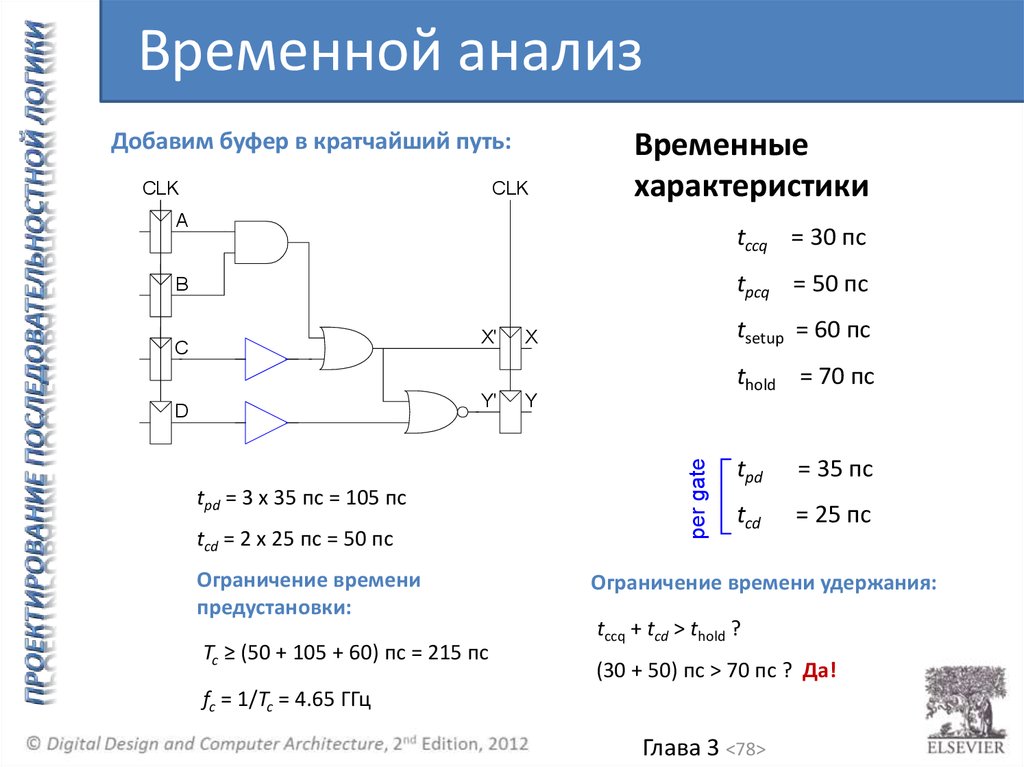
Временной анализ
Добавим буфер в кратчайший путь:
CLK
CLK
Временные
характеристики
A
tccq = 30 пс
tpcq = 50 пс
B
Y'
D
tpd = 3 x 35 пс = 105 пс
tcd = 2 x 25 пс = 50 пс
Ограничение времени
предустановки:
Tc ≥ (50 + 105 + 60) пс = 215 пс
tsetup = 60 пс
X
thold = 70 пс
Y
per gate
X'
C
tpd
= 35 пс
tcd
= 25 пс
Ограничение времени удержания:
tccq + tcd > thold ?
(30 + 50) пс > 70 пс ? Да!
fc = 1/Tc = 4.65 ГГц
Глава 3 <78>

79.

Расфазировка тактовых сигналов
• Тактовые импульсы поступают на разные регистры схемы не
одновременно
• Расфазировка: различие во времени между фронтами тактовых
сигналов разных элементов
• Следует выполнить анализ худшего случая, чтобы
гарантировать выполнение динамической дисциплины для всех
регистров схемы!
delay
CLK
CLK1
CLK2
Q1
R1
C
L
D2
R2
t skew
CLK1
CLK2
CLK
Глава 3 <79>

80.

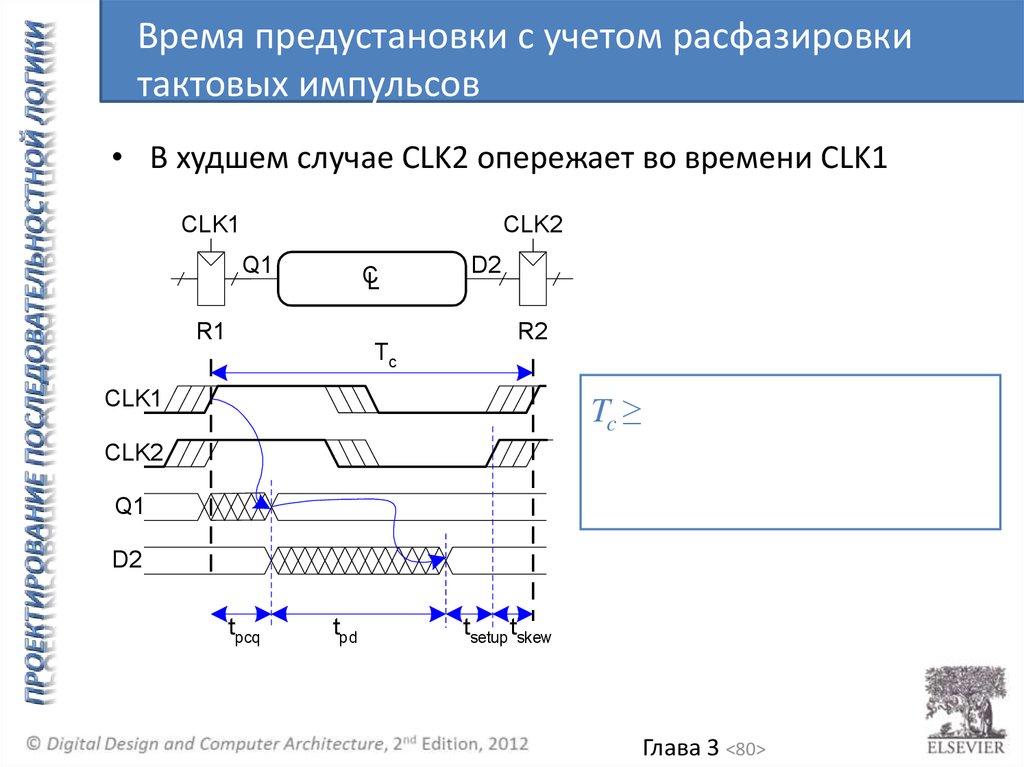
Время предустановки с учетом расфазировки
тактовых импульсов
• В худшем случае CLK2 опережает во времени CLK1
CLK1
CLK2
Q1
C
L
R1
Tc
D2
R2
CLK1
Tc ≥
CLK2
Q1
D2
tpcq
tpd
tsetup tskew
Глава 3 <80>

81.

Ограничение времени предустановки с учетом
расфазировки тактовых импульсов
• В худшем случае CLK2 опережает во времени CLK1
CLK1
CLK2
Q1
C
L
R1
Tc
D2
R2
CLK1
Tc ≥ tpcq + tpd + tsetup + tskew
tpd ≤
CLK2
Q1
D2
tpcq
tpd
tsetup tskew
Глава 3 <81>

82.

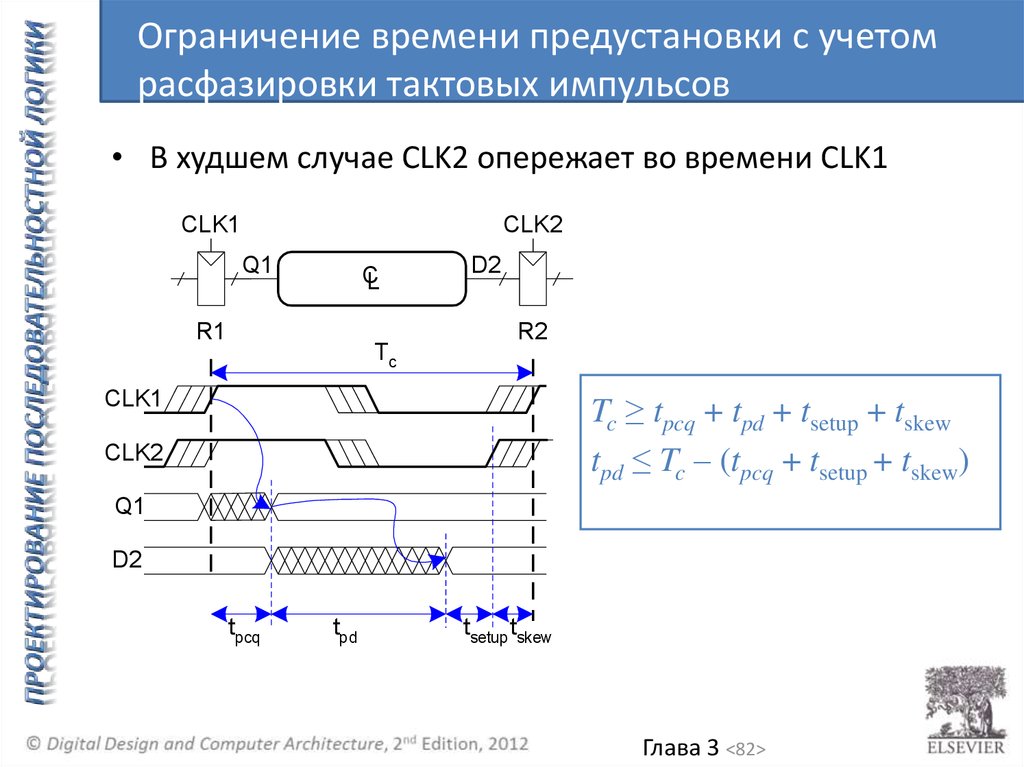
Ограничение времени предустановки с учетом
расфазировки тактовых импульсов
• В худшем случае CLK2 опережает во времени CLK1
CLK1
CLK2
Q1
C
L
R1
Tc
D2
R2
CLK1
Tc ≥ tpcq + tpd + tsetup + tskew
tpd ≤ Tc – (tpcq + tsetup + tskew)
CLK2
Q1
D2
tpcq
tpd
tsetup tskew
Глава 3 <82>

83.

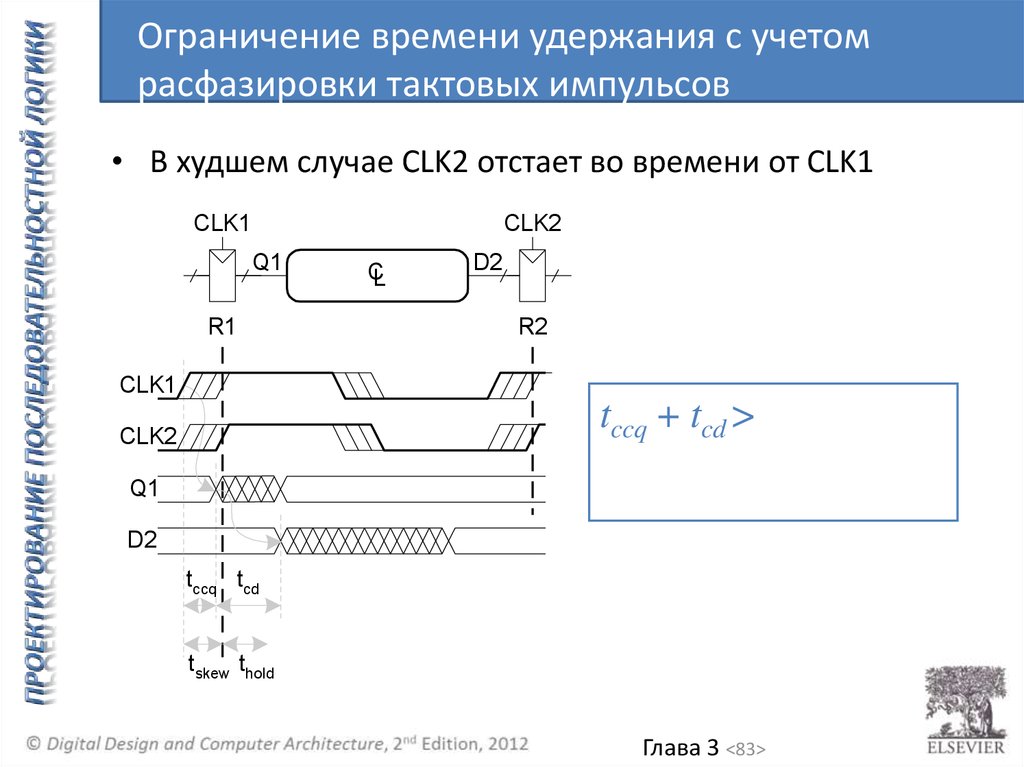
Ограничение времени удержания с учетом
расфазировки тактовых импульсов
• В худшем случае CLK2 отстает во времени от CLK1
CLK1
CLK2
Q1
R1
CL
D2
R2
CLK1
tccq + tcd >
CLK2
Q1
D2
tccq tcd
tskew thold
Глава 3 <83>

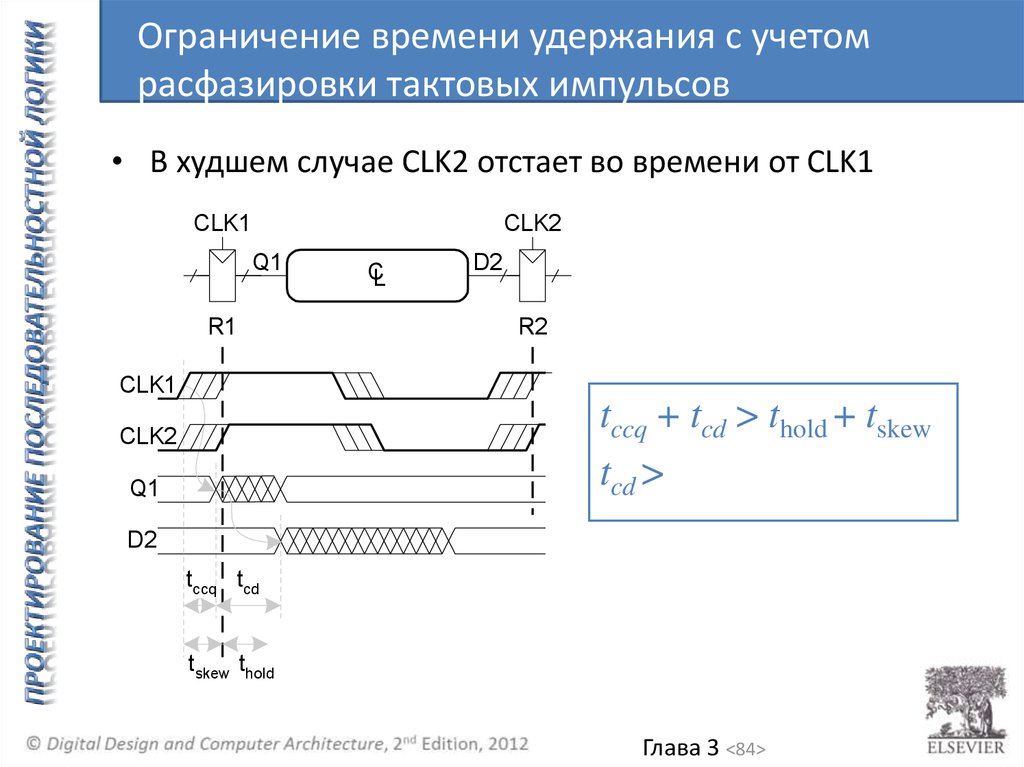
84.

Ограничение времени удержания с учетом
расфазировки тактовых импульсов
• В худшем случае CLK2 отстает во времени от CLK1
CLK1
CLK2
Q1
R1
CL
D2
R2
CLK1
tccq + tcd > thold + tskew
tcd >
CLK2
Q1
D2
tccq tcd
tskew thold
Глава 3 <84>

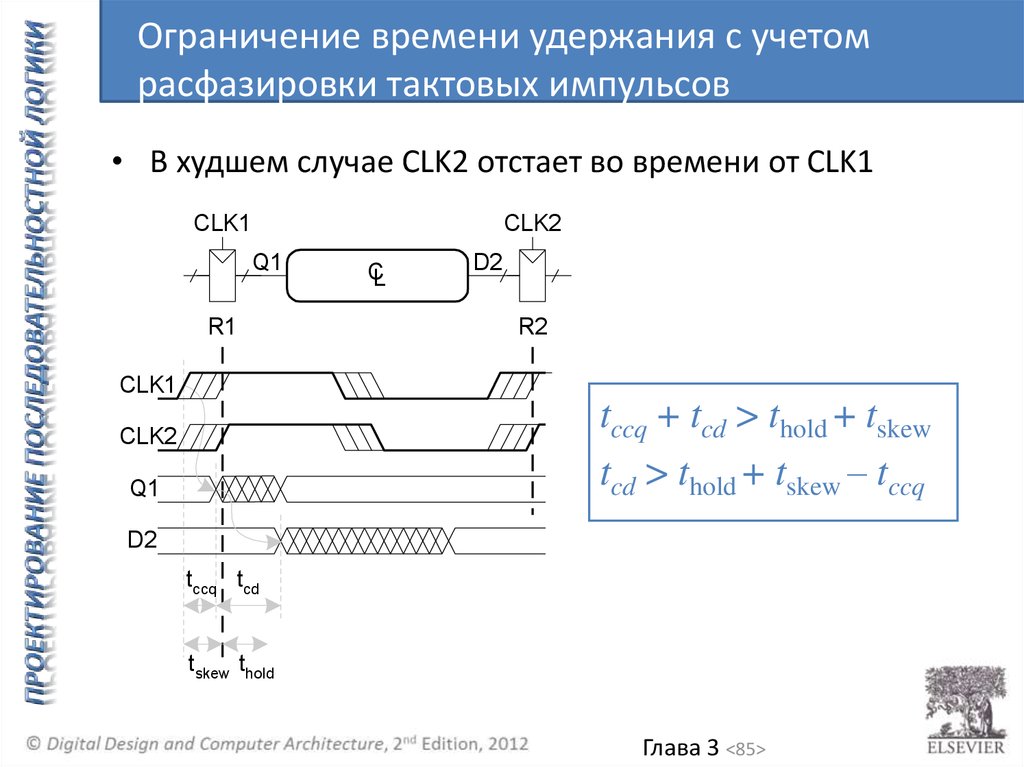
85.

Ограничение времени удержания с учетом
расфазировки тактовых импульсов
• В худшем случае CLK2 отстает во времени от CLK1
CLK1
CLK2
Q1
R1
CL
D2
R2
CLK1
tccq + tcd > thold + tskew
tcd > thold + tskew – tccq
CLK2
Q1
D2
tccq tcd
tskew thold
Глава 3 <85>

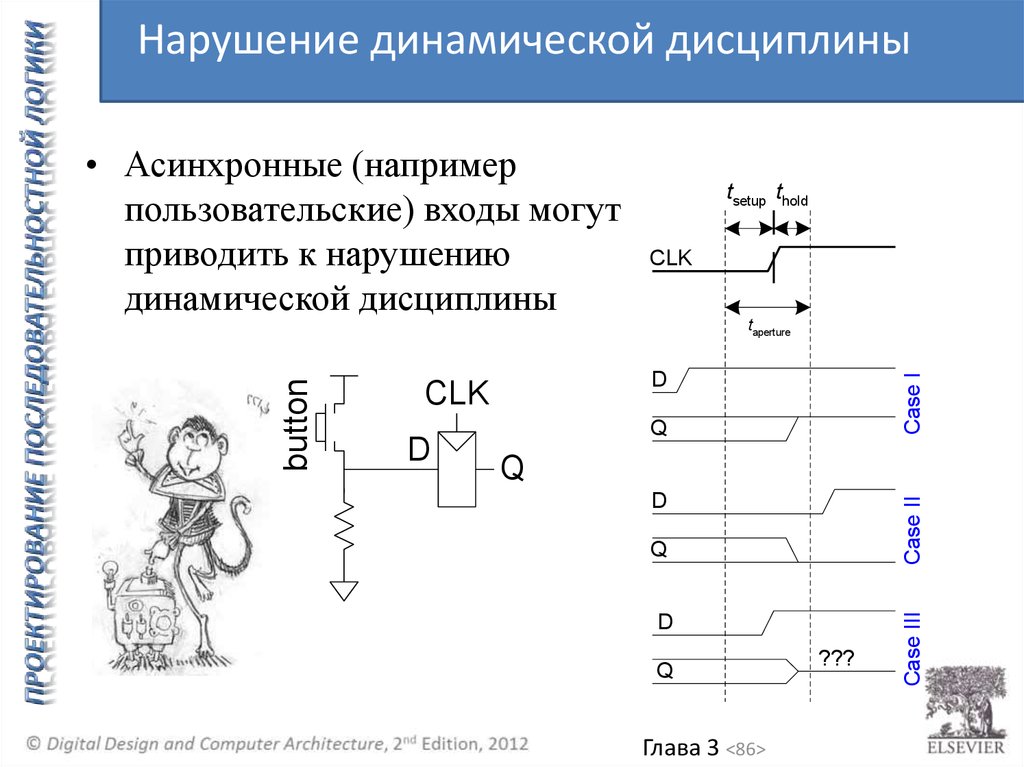
86.

Нарушение динамической дисциплины
• Асинхронные (например
пользовательские) входы могут
приводить к нарушению
динамической дисциплины
tsetup thold
CLK
Q
Q
D
Case II
D
Case I
D
CLK
Q
D
Q
Глава 3 <86>
???
Case III
button
taperture

87.

Метастабильность
• Бистабильные приборы: два стабильные состояния
и метастабильное состояние между ними
• Триггер два стабильные состояния (0 и 1) и одно
метастабильное состояние
• Если триггер попадает в метастабильное состояние,
он может находится в нем неограниченно долго
metastable
stable
stable
Глава 3 <87>

88.

Внутренняя структура триггера
• Триггер имеет обратную связь: если Q находится где-то между 1
и 0, то перекрестно соединенные элементы устанавливают выход
в одно из двух состояний (1 или 0)
R
S
N1
Q
N2
Q
• Метастабильный сигнал: если он не принял корректное значение 0
или 1
• Если вход триггера изменяется в случайный момент, вероятность
того, что его выход Q будет в метастабильном состоянии спустя
время t:
P(tres > t) = (T0/Tc ) e-t/τ
tres
: время разрешения в 1 или 0 T0, τ : характеристики схемы
Глава 3 <88>

89.

Метастабильность
• Интуитивно:
– T0/Tc: вероятность изменения входа в плохое (апертурное)
время
P(tres > t) = (T0/Tc ) e-t/τ
– τ: константа, определяющая как быстро триггер уходит из
метастабильного состояния
P(tres > t) = (T0/Tc ) e-t/τ
• Коротко, если триггер фиксирует метастабильный
вход, то после достаточно продолжительного
ожидания (t) он, с высокой вероятностью, перейдет в
стабильное состояние 0 или 1
Глава 3 <89>

90.

Синхронизаторы
• Наличие асинхронных входов неизбежно
(интерфейс пользователя, системы с разными
тактовыми сигналами и т.д.)
• Функция синхронизатора: сделать вероятность
сбоя (выход Q находится в метастабильном
состоянии) достаточно малой
• Синхронизатор не может довести вероятность сбоя
до 0
CLK
SYNC
D
Q
Глава 3 <90>

91.

Внутренняя структура синхронизатора
• Синхронизатор: строится из двух последовательно соединенных
триггеров
• Предположим, что D изменяется во время фиксации F1
• У внутреннего сигнала D2 есть время (Tc - tsetup) для разрешения в
CLK
CLK
1 или 0
D2
D
Q
F1
F2
Tc
CLK
D2
metastable
Q
tres
t
setup
Глава 3 <91>
tpcq

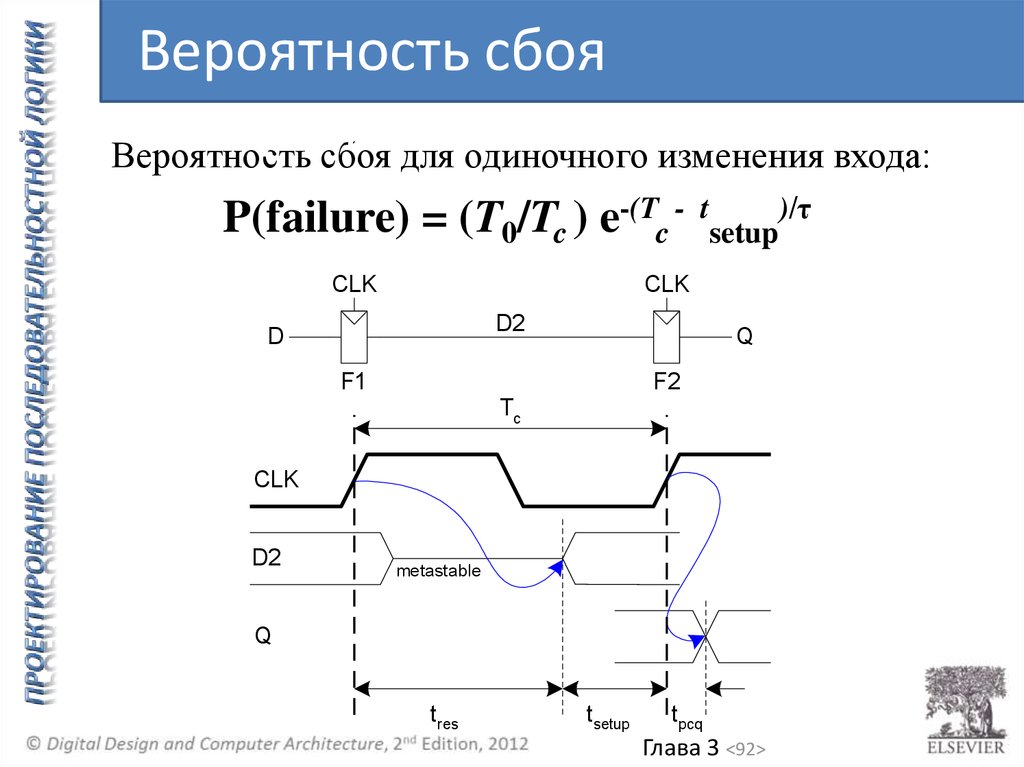
92.

Вероятность сбоя
синхронизатора
Вероятность сбоя для одиночного изменения входа:
P(failure) = (T0/Tc ) e-(Tc CLK
t
)/τ
setup
CLK
D2
D
Q
F1
F2
Tc
CLK
D2
metastable
Q
tres
tsetup
tpcq
Глава 3 <92>

93.

Среднее время между сбоями синхронизатора
• Если асинхронный вход изменяется один раз за секунду, то
вероятность сбоя за одну секунду будет равна P(failure)
• Если вход изменяется N раз за секунду, то вероятность
отказа за секунду будет:
P(failure)/с= (NT0/Tc) e-(Tc -
t
)/τ
setup
• Сбой синхронизатора происходит в среднем 1/[P(failure)/с]
• Эта величина называется средним временем наработки
на отказ (mean time between failures, MTBF):
MTBF = 1/[P(failure)/с] = (Tc/NT0) e(Tc Глава 3 <93>
t
)/τ
setup

94.

Пример синхронизатора
CLK
CLK
D2
D
F1
Q
F2
• Предположим:
Tc = 1/500 МГц = 2 нс
τ = 200 пс
T0 = 150 пс
tsetup = 100 пс
N = 1 событий за секунду
• Чему равна вероятность отказа? MTBF?
Глава 3 <94>

95.

Пример синхронизатора
CLK
CLK
D2
D
F1
Q
F2
• Предположим:
Tc = 1/500 МГц = 2 нс
τ = 200 пс
T0 = 150 пс
tsetup = 100 пс
N = 1 событий за секунду
• Чему равна вероятность отказа? MTBF?
P(failure) = (150 пс/2 нс) e-(1.9 нс)/200 пс
= 5.6 × 10-6
P(failure)/с= 10 × (5.6 × 10-6 )
= 5.6 × 10-5 / с
MTBF = 1/[P(failure)/с] ≈ 5 часов
Глава 3 <95>

96.

Параллелизм
• Два типа параллелизма:
– Пространственный параллелизм:
• несколько копий аппаратных блоков в одно и то
же время выполняют несколько задач
– Временной параллелизм:
• разбиение задачи на несколько ступеней
• также называется конвейеризацией
• например, сборочная линия
Глава 3 <96>

97.

Определения параллелизма
• Токен (Token): Набор входной информации, который
обрабатывается для того, чтобы получить выходную
информацию
• Латентность (latency): Время прохождения одного
токена через всю систему с ее входа на выход
• Пропускная способность (throughput): Количество
токенов, которое обрабатывается системой в единицу
времени
Параллелизм увеличивает пропускную способность
Глава 3 <97>

98.

Пример параллелизма
• Бен готовит печенье для вечеринки, посвященной
введению в эксплуатацию его контроллера светофора
• 5 минут уходит на сворачивание печенья на один
противень
• В течение 15 минут печенье выпекается
• Чему равна пропускная способность и задержка без
параллелизма?
Глава 3 <98>

99.

Пример параллелизма
• Бен готовит печенье для вечеринки, посвященной
введению в эксплуатацию его контроллера светофора
• 5 минут уходит на сворачивание печенья на один
противень
• В течение 15 минут печенье выпекается
• Чему равна пропускная способность и задержка без
параллелизма?
Латентность = 5 + 15 = 20 минут = 1/3 час
Пропускная способность = 1 противень/ 1/3 час= 3
противня/час
Глава 3 <99>

100.

Пример параллелизма
• Чему равна пропускная способность и
задержка если Бен использует
параллелизма?
– Пространственный параллелизм: Бен просит
Алису помочь, используя ее печь
– Временной параллелизм:
• Две ступени: сворачивание и выпекание
• Он использует два противня
• Когда первая партия выпекается, он
сворачивает следующую партию и т.д.
Глава 3 <100>

101.

Пространственный параллелизм:
Latency:
time to
first tray
0
5
10
15
20
25
30
35
40
45
50
Spatial
Parallelism
Time
Tray 1
Ben 1
Ben 1
Tray 2
Alyssa 1
Alyssa 1
Roll
Tray 3
Ben 2
Ben 2
Tray 4
Alyssa 2
Alyssa 2
Латентность = ?
Пропускная способность = ?
Глава 3 <101>
Bake
Legend

102.

Пространственный параллелизм:
Latency:
time to
first tray
0
5
10
15
20
25
30
35
40
45
50
Spatial
Parallelism
Time
Tray 1
Ben 1
Ben 1
Tray 2
Alyssa 1
Alyssa 1
Roll
Tray 3
Ben 2
Ben 2
Tray 4
Alyssa 2
Alyssa 2
Латентность = 5 + 15 = 20 минут = 1/3 час
Пропускная способность = 2 противня/ 1/3 час= 6
противней/час
Глава 3 <102>
Bake
Legend

103.

Временной параллелизм
Latency:
time to
first tray
0
5
10
15
20
25
30
35
40
45
50
Temporal
Parallelism
Time
Tray 1
Tray 2
Tray 3
Ben 1
Ben 1
Ben 2
Ben 2
Ben 3
Ben 3
Латентность = ?
Пропускная способность = ?
Глава 3 <103>

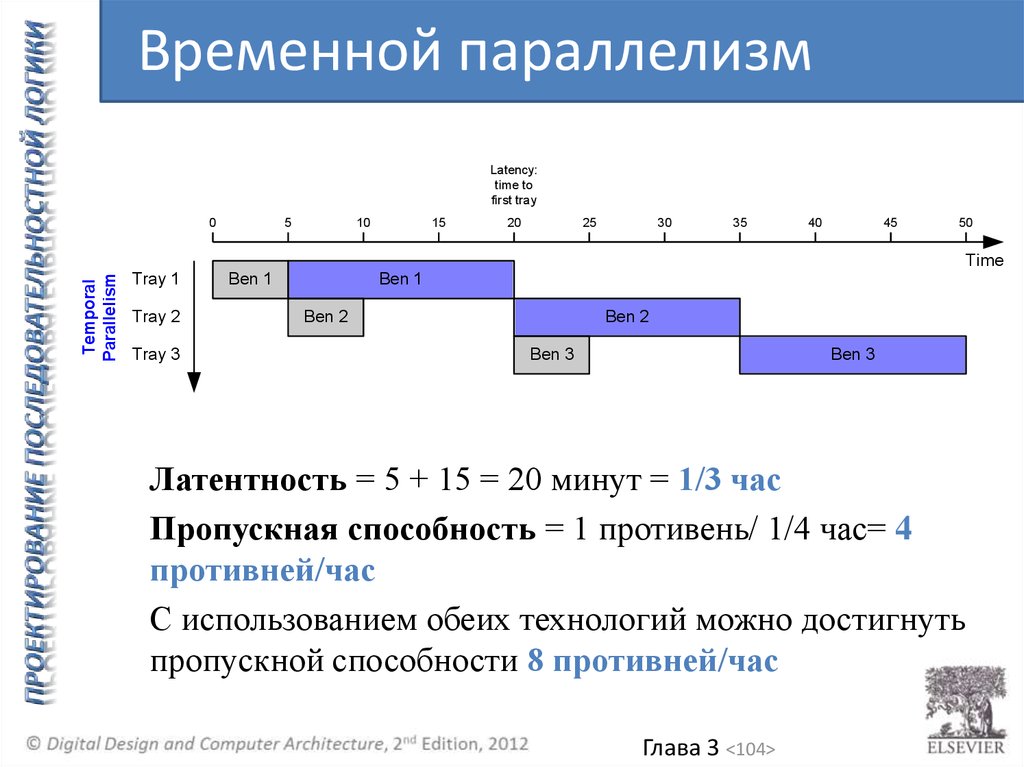
104.

Временной параллелизм
Latency:
time to
first tray
0
5
10
15
20
25
30
35
40
45
50
Temporal
Parallelism
Time
Tray 1
Tray 2
Tray 3
Ben 1
Ben 1
Ben 2
Ben 2
Ben 3
Ben 3
Латентность = 5 + 15 = 20 минут = 1/3 час
Пропускная способность = 1 противень/ 1/4 час= 4
противней/час
С использованием обеих технологий можно достигнуть
пропускной способности 8 противней/час
Глава 3 <104>