Цифровая схемотехника и архитектура компьютера. Цифровые функциональные узлы. (Глава 5)

1.

Глава 5
Цифровая схемотехника и архитектура
компьютера, второе издание
Дэвид М. Харрис и Сара Л. Харрис
Глава 5 <1>

2.

Цифровая схемотехника и архитектура компьютера
Эти слайды предназначены для преподавателей, которые читают
лекции на основе учебника «Цифровая схемотехника и
архитектура компьютера» авторов Дэвида Харриса и Сары
Харрис. Бесплатный русский перевод второго издания этого
учебника можно загрузить с сайта компании Imagination
Technologies:
https://community.imgtec.com/downloads/digital-design-andcomputer-architecture-russian-edition-second-edition
Процедура регистрации на сайте компании Imagination
Technologies описана на станице:
http://www.silicon-russia.com/2016/08/04/harris-and-harris-2/
Глава 5 <2>

3.

Благодарности
Перевод данных слайдов на русский язык был выполнен командой
сотрудников университетов и компаний из России, Украины, США в составе:
Александр Барабанов - доцент кафедры компьютерной инженерии факультета радиофизики,
электроники и компьютерных систем Киевского национального университета имени Тараса
Шевченко, кандидат физ.-мат. наук, Киев, Украина;
Антон Брюзгин - начальник отдела АО «Вибро-прибор», Санкт-Петербург, Россия.
Евгений Короткий - доцент кафедры конструирования электронно-вычислительной аппаратуры
факультета электроники Национального технического университета Украины «Киевский
Политехнический Институт», руководитель открытой лаборатории электроники Lampa, кандидат
технических наук, Киев, Украина;
Евгения Литвинова – заместитель декана факультета компьютерной инженерии и управления,
доктор технических наук, профессор кафедры автоматизации проектирования вычислительной
техники Харьковского национального университета радиоэлектроники, Харьков, Украина;
Юрий Панчул - старший инженер по разработке и верификации блоков микропроцессорного
ядра в команде MIPS I6400, Imagination Technologies, отделение в Санта-Кларе, Калифорния, США;
Дмитрий Рожко - инженер-программист АО «Вибро-прибор», магистр Санкт-Петербургского
государственного автономного университета аэрокосмического приборостроения (ГУАП), СанктПетербург, Россия;
Владимир Хаханов – декан факультета компьютерной инженерии и управления, проректор по
научной работе, доктор технических наук, профессор кафедры автоматизации проектирования
вычислительной техники Харьковского национального университета радиоэлектроники, Харьков,
Украина;
Светлана Чумаченко – заведующая кафедрой автоматизации проектирования вычислительной
техники Харьковского национального университета радиоэлектроники, доктор технических наук,
профессор, Харьков, Украина.
Глава 5 <3>

4.

Глава 5 :: Темы
Введение
Арифметические схемы
Представление чисел
Последовательностные
функциональные блоки
• Матрицы памяти
• Матрицы логических
элементов
Глава 5 <4>

5.

Введение
• Цифровые функциональные блоки:
– Логические элементы, мультиплексоры, декодеры,
регистры, схемы арифметики, счетчики, матрицы
памяти и матрицы логических элементов
• Функциональные блоки демонстрируют
принципы иерархичности, модульности и
регулярности проектируемых систем
– Иерархия более простых компонентов
– Строго определенные интерфейсы и функции
– Регулярная структура легко масштабируется в системы
различных размеров
• Подобные функциональные блоки будут
использованы в главе 7 для проектирования
микропроцессора
Глава 5 <5>

6.

Одноразрядный сумматор. 1
Half
Adder
Full
Adder
A
A
Cout
B
Cout
+
B
0
1
0
1
S
=
Cout =
Cout
Cin
+
S
A
0
0
1
1
B
S
S
Cin
0
0
0
0
1
1
1
1
A
0
0
1
1
0
0
1
1
B
0
1
0
1
0
1
0
1
Cout
S
S =
Cout =
Глава 5 <6>

7.

Одноразрядный сумматор. 2
Half
Adder
Full
Adder
A
A
Cout
B
Cout
+
B
0
1
0
1
S
=
Cout =
Cout
0
0
0
1
Cin
+
S
A
0
0
1
1
B
S
S
0
1
1
0
Cin
0
0
0
0
1
1
1
1
A
0
0
1
1
0
0
1
1
B
0
1
0
1
0
1
0
1
Cout
0
0
0
1
0
1
1
1
S
0
1
1
0
1
0
0
1
S =
Cout =
Глава 5 <7>

8.

Одноразрядный сумматор. 3
Half
Adder
Full
Adder
A
A
Cout
B
Cout
+
B
0
1
0
1
Cout
0
0
0
1
S
=A B
Cout = AB
Cin
+
S
A
0
0
1
1
B
S
S
0
1
1
0
Cin
0
0
0
0
1
1
1
1
A
0
0
1
1
0
0
1
1
B
0
1
0
1
0
1
0
1
Cout
0
0
0
1
0
1
1
1
S
0
1
1
0
1
0
0
1
S = A B Cin
Cout = AB + ACin + BCin
Глава 5 <8>

9.

Многоразрядные сумматоры
• Типы распространения переносов:
– Последовательный
(медленный)
– Ускоренный групповой
(быстрый)
– Префиксный
(самый быстрый)
• Два последних типа используются для
многоразрядных сумматоров, но их реализация
требует дополнительных аппаратных затрат
A
Условное
обозначение Cout
B
N
N
+
Cin
N
S
Глава 5 <9>

10.

Сумматор с последовательным переносом
• Цепь одноразрядных сумматоров
• Перенос проходит через всю цепочку
• Недостаток: медленное суммирование
A31
Cout
B31
+
S31
A30
C30
B30
+
S30
C29
A1
C1
B1
+
A0
C0
S1
Глава 5 <10>
B0
+
S0
Cin

11.

Сумматор с последовательным переносом
Задержка сумматора складывается из задержек
разрядов в каждом звене:
tripple = NtFA
где tFA – задержка одного полного сумматора
Глава 5 <11>

12.

Сумматор с ускоренным групповым переносом
(СУГП)
• Определить значение переноса (Cout) в каждом блоке k-разрядного
сумматора, используя сигналы generate и propagate
Некоторые определения:
– Разряд i формирует перенос либо путем его генерирования (generating)
либо путем распространения (propagating) переноса со своего
соответствующего входа на свой выход
– Генерирование (Gi) и распространение (Pi) сигналов для каждого
разряда:
• Разряд i будет генерировать перенос, если Ai и Bi (оба) равны 1.
Gi = Ai Bi
• Разряд i будет распространять перенос от соответствующего входа к
соответствующему выходу, если Ai или Bi равен 1.
Pi = Ai + Bi
• Перенос разряда i (Ci):
Ci = Ai Bi + (Ai + Bi )Ci-1 = Gi + Pi Ci-1
Глава 5 <12>

13.

Суммирование с ускоренным групповым переносом
• Шаг1: Вычислить Gi и Pi для всех разрядов
• Шаг 2: Вычислить G и P для всех kбитовых блоков сумматора
• Шаг 3: Перенос Cin распространяется
через все k-битовые блоки
генерации/распространения
Глава 5 <13>

14.

Сумматор с ускоренным групповым переносом
• Пример: 4-разрядные блоки (G3:0 и P3:0) :
G3:0 = G3 + P3 (G2 + P2 (G1 + P1G0 )
P3:0 = P3P2 P1P0
• В общем случае,
Gi:j = Gi + Pi (Gi-1 + Pi-1 (Gi-2 + Pi-2Gj )
Pi:j = PiPi-1 Pi-2Pj
Ci = Gi:j + Pi:j Ci-1
Глава 5 <14>

15.

32-разрядный сумматор с ускоренным групповым
переносом с 4-разрядными блоками
B31:28 A31:28
Cout
B27:24 A27:24
B7:4 A7:4
4-bit CLA C27 4-bit CLA C23
Block
Block
S31:28
C7 4-bit CLA C3 4-bit CLA
Block
Block
S27:24
B3
A3
B3:0 A3:0
S7:4
B2
A2
C2
B1
S3:0
A1
C1
B0
A0
C0
+
+
+
+
S3
S2
S1
S0
G3:0
G3
P3
G2
P2
G1
P1
G0
P3:0
Cout
Cin
Cin
P3
P2
P1
P0
Глава 5 <15>
Cin

16.

Задержки сумматор с ускоренным групповым
переносом
Для N-разрядного сумматор с ускоренным групповым
переносом с k-разрядными блоками:
tCLA = tpg + tpg_block + (N/k – 1)tAND_OR + ktFA
– tpg :
задержка генерации всех Pi, Gi
– tpg_block : задержка генерации всех Pi:j, Gi:j
– tAND_OR : задержка тракта вход Cin - выход Cout из элементов
И/ИЛИ в k-разрядном блоке сумматор с ускоренным групповым
переносом
N-разрядный сумматор с ускоренным групповым
переносом практически всегда более быстрый, чем
сумматор с последовательным переносом для N > 16
Глава 5 <16>

17.

Префиксный сумматор
• Вычисляет перенос на входе (Ci-1) для каждого
разряда, затем вычисляет сумму:
Si = (Ai Bi) Ci
• Вычисляет G и P для 1-, 2-, 4-, 8-разрядов
блоков, до тех пор, пока не станут известны все
переносы Gi (входные переносы всех разрядов)
• Количество каскадов log2N
Глава 5 <17>

18.

Префиксный сумматор
• Перенос на входе либо генерируется для данного
разряда либо распространяется от предыдущего.
• Разряд -1 соответствует Cin, тогда
G-1 = Cin, P-1 = 0
• Значение переноса на входе разряда i равно значению
переноса на выходе разряда i-1:
Ci-1 = Gi-1:-1
Gi-1:-1: сигнал генерации блока разрядов от i-1 до -1
• Выражение для суммы:
Si = (Ai Bi) Gi-1:-1
• Цель: быстрое вычисление G0:-1, G1:-1, G2:-1, G3:-1, G4:-1,
G5:-1, … (называемых префиксами)
Глава 5 <18>

19.

Префиксный сумматор
• Сигналы генерации и распространения блока,
охватывающего разряды i:j:
Gi:j = Gi:k + Pi:k Gk-1:j
Pi:j = Pi:kPk-1:j
• Более детально:
– Генерация: блок i:j генерирует перенос, если:
• Старшие разряды (i:k) генерируют перенос или
• Старшие разряды распространяют перенос,
сгенерированный в младших разрядах (k-1:j)
– Распространение: блок i:j распространяет перенос,
если и старшие и младшие разряды распространяют
перенос
Глава 5 <19>

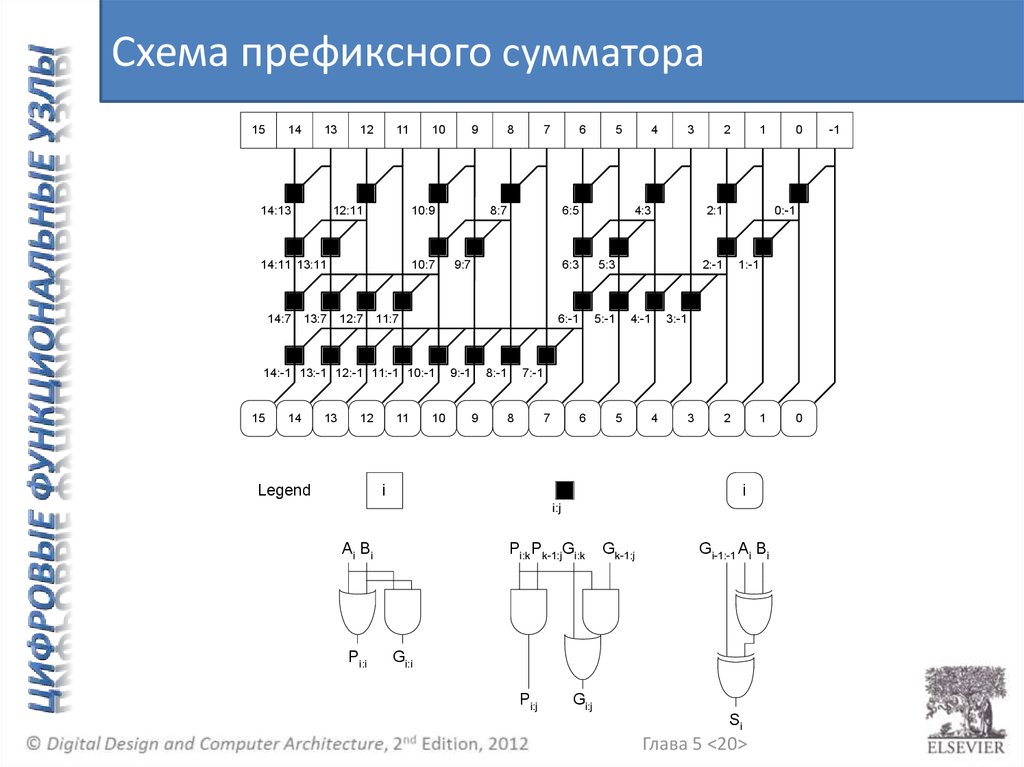
20.

Схема префиксного сумматора
15
14
13
14:13
12
11
12:11
13:7
10:7
12:7
14
13
12
Legend
8
7
11
10
6
8:7
9:7
9:-1
8:-1
9
5
6:5
11:7
14:-1 13:-1 12:-1 11:-1 10:-1
15
9
10:9
14:11 13:11
14:7
10
4
3
4:3
6:3
5:3
6:-1
5:-1
2
1
2:1
0:-1
2:-1
4:-1
1:-1
3:-1
7:-1
8
7
6
5
4
3
2
i
1
i
i:j
Ai Bi
Pi:i
0
Pi:k Pk-1:jGi:k
Gk-1:j
Gi-1:-1 Ai Bi
Gi:i
Pi:j
Gi:j
Si
Глава 5 <20>
0
-1

21.

Задержка префиксного сумматора
tPA = tpg + log2N(tpg_prefix ) + tXOR
– tpg: задержка формирования Pi Gi (элементы И или ИЛИ)
– tpg_prefix: задержка черной префиксной ячейки (элементы ИИЛИ)
Глава 5 <21>

22.

Сравнение задержек сумматоров
Сравнить задержки: 32-разрядный сумматор с последовательным
переносом, сумматор с ускоренным групповым переносом, и
префиксного сумматора
• сумматор с ускоренным групповым переносом содержит 4разрядные блоки
• Задержка 2-входового вентиля = 100 ps; задержка полного сумматора
= 300 ps
Глава 5 <22>

23.

Сравнение задержек сумматоров
Сравнить задержки: 32-разрядный сумматор с последовательным
переносом, сумматор с ускоренным групповым переносом и
префиксный сумматор
• сумматор с ускоренным групповым переносом содержит 4разрядные блоки
• Задержка 2-входового вентиля = 100 ps; задержка полного сумматора
= 300 ps
tripple
tCLA
tPA
= NtFA = 32(300 ps)
= 9.6 ns
= tpg + tpg_block + (N/k – 1)tAND_OR + ktFA
= [100 + 600 + (7)200 + 4(300)] ps
= 3.3 ns
= tpg + log2N(tpg_prefix ) + tXOR
= [100 + log232(200) + 100] ps
= 1.2 ns
Глава 5 <23>

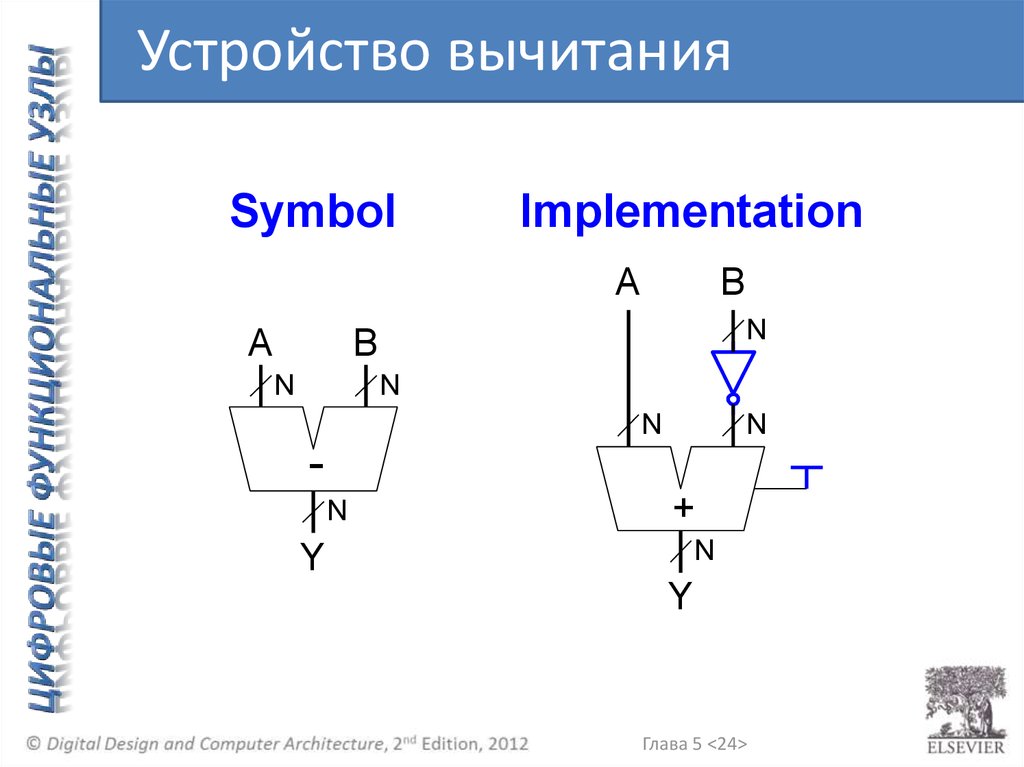
24.

Устройство вычитания
Symbol
Implementation
A
A
B
N
B
N
N
N
N
N
+
N
Y
Y
Глава 5 <24>

25.

Компаратор: Сравнение на равенство
Symbol
Implementation
A3
B3
A
B
4
4
=
Equal
A2
B2
Equal
A1
B1
A0
B0
Глава 5 <25>

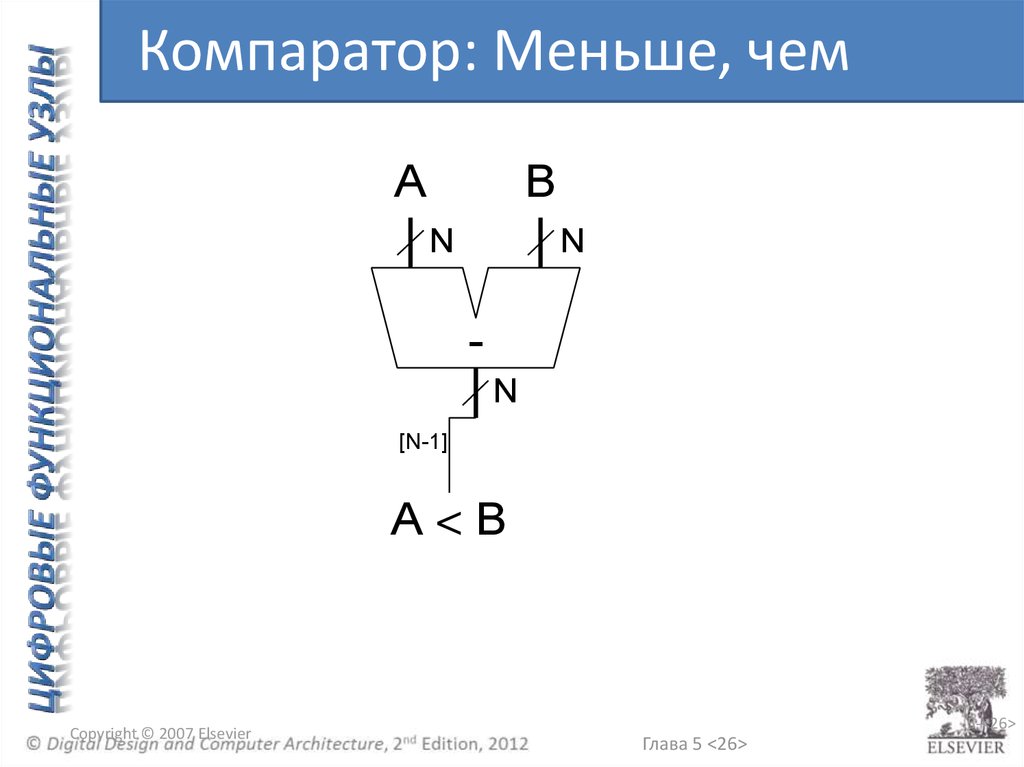
26.

Компаратор: Меньше, чем
A
B
N
N
N
[N-1]
A<B
Copyright © 2007 Elsevier
5-<26>
Глава 5 <26>

27.

Арифметико-логическое устройство (АЛУ)
A
B
N
N
ALU
N
Y
Copyright © 2007 Elsevier
3F
F2:0
Функция
000
A&B
001
A|B
010
A+B
011
Не используется
100
A & ~B
101
A | ~B
110
A-B
111
SLT
5-<27>
Глава 5 <27>

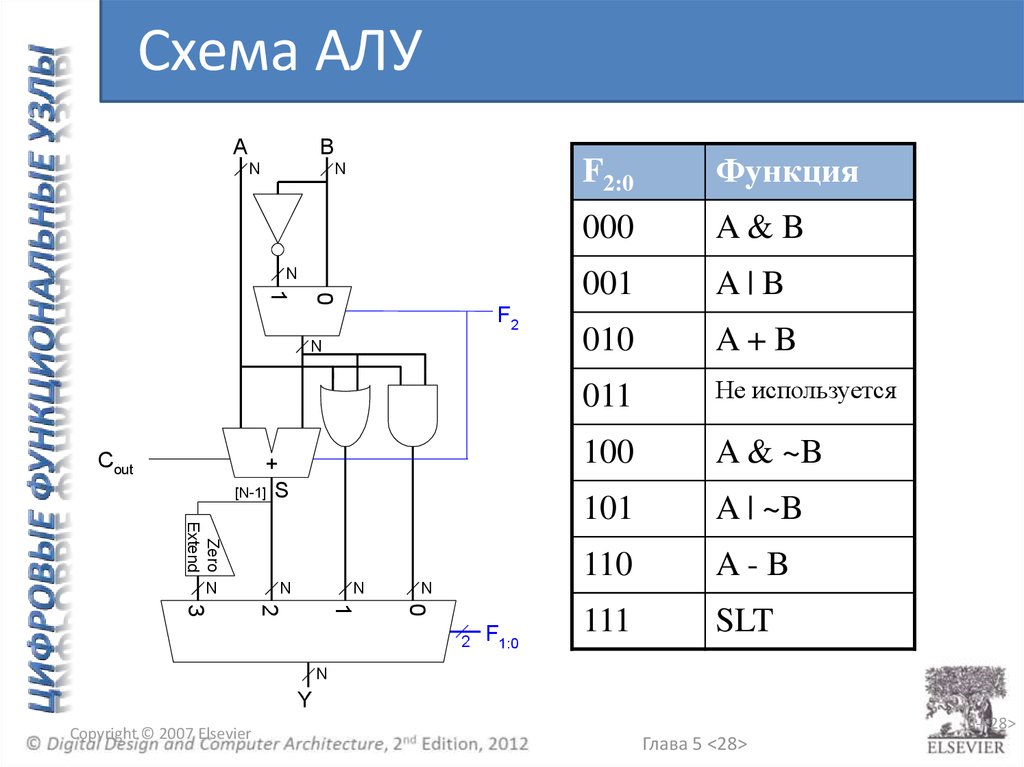
28.

Схема АЛУ
A
B
N
N
N
0
1
F2
N
Cout
+
[N-1] S
Zero
Extend
N
N
N
N
0
1
2
3
2
F1:0
F2:0
Функция
000
A&B
001
A|B
010
A+B
011
Не используется
100
A & ~B
101
A | ~B
110
A-B
111
SLT
N
Y
Copyright © 2007 Elsevier
5-<28>
Глава 5 <28>

29.

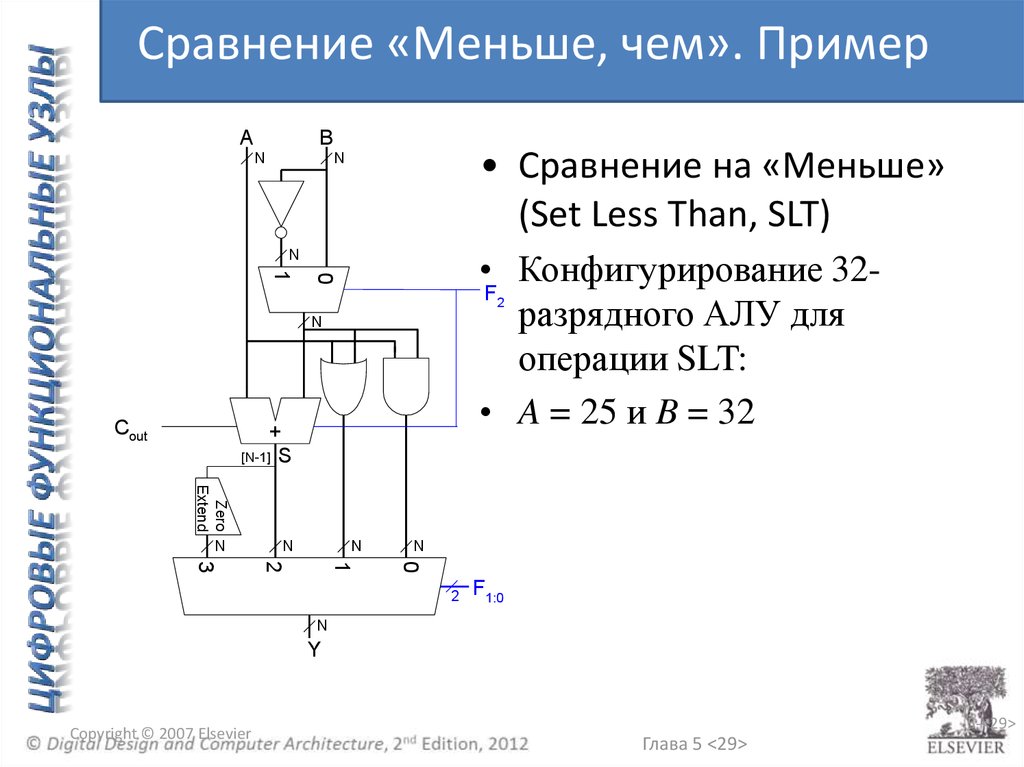
Сравнение «Меньше, чем». Пример
A
B
N
• Сравнение на «Меньше»
(Set Less Than, SLT)
N
• Конфигурирование 32F
разрядного АЛУ для
операции SLT:
• A = 25 и B = 32
N
0
1
2
N
Cout
+
[N-1] S
Zero
Extend
N
N
N
N
0
1
2
3
2
F1:0
N
Y
Copyright © 2007 Elsevier
5-<29>
Глава 5 <29>

30.

Сравнение «Меньше, чем». Пример
A
• Конфигурирование 32разрядного АЛУ для операции
SLT: A = 25 и B = 32
B
N
N
N
0
1
F2
N
Cout
+
[N-1] S
Zero
Extend
N
N
N
N
0
1
2
3
2
N
Y
Copyright © 2007 Elsevier
F1:0
– A < B, поэтому Y должен быть
32-разрядным представлением
1 (0x00000001)
– F2:0 = 111
– F2 = 1 (сумматор работает как
вычитатель): 25 - 32 = -7
– -7 имеет 1 в старшем разряде
(S31 = 1)
– F1:0 = 11 мультиплексор
выбирает Y = S31 (дополнение
нулями) = 0x00000001.
5-<30>
Глава 5 <30>

31.

Устройство сдвига (Shifter)
Логическое устройство сдвига: смещает сдвигаемое значение влево
или вправо и заполняет пустые разряды нулями «0»
Пример: 11001 >> 2 =
Пример 11001 << 2 =
Арифметическое устройство сдвига: при сдвиге влево работает так же,
как и логическое, а при сдвиге вправо заполняет пустые разряды
значением старшего бита (most significant bit, msb).
Пример 11001 >>> 2 =
Пример : 11001 <<< 2 =
Циклический сдвиг: сдвигает биты по кругу, таким образом, что
уходящий бит появляется на месте появившегося свободного разряда
на другом конце числа
Пример : 11001 ROR 2 =
Пример : 11001 ROL 2 =
Copyright © 2007 Elsevier
5-<31>
Глава 5 <31>

32.

Устройства сдвига
• Логическое устройство сдвига:
– Ex: 11001 >> 2 = 00110
– Ex: 11001 << 2 = 00100
• Арифметическое устройство сдвига:
– Ex: 11001 >>> 2 = 11110
– Ex: 11001 <<< 2 = 00100
• Циклическое устройство сдвига:
– Ex: 11001 ROR 2 = 01110
– Ex: 11001 ROL 2 = 00111
Глава 5 <32>

33.

Схема устройства сдвига
A 3 A 2 A1 A0
shamt1:0
2
00
S1:0
01
Y3
10
shamt1:0
11
2
00
S1:0
01
A3:0
4
>>
4
Y2
10
Y3:0
11
00
S1:0
01
Y1
10
11
00
01
10
11
Глава 5 <33>
S1:0
Y0

34.

Устройство сдвига как умножитель и делитель
• A << N = A × 2N
– Пример: 00001 << 2 = 00100 (1 × 22 = 4)
– Пример : 11101 << 2 = 10100 (-3 × 22 = -12)
• A >>> N = A ÷ 2N
– Пример : 01000 >>> 2 = 00010 (8 ÷ 22 = 2)
– Пример : 10000 >>> 2 = 11100 (-16 ÷ 22 = -4)
Глава 5 <34>

35.

Устройство умножения
• Частичное произведение, формируемое путем
умножения текущего разряда множителя на все
разряды множимого
• Сдвинутые частичные произведения,
суммированные для формирования результата
Decimal
230
x 42
460
+ 920
9660
Binary
multiplicand
multiplier
partial
products
result
230 x 42 = 9660
0101
x 0111
0101
0101
0101
+ 0000
0100011
5 x 7 = 35
Глава 5 <35>

36.

Умножитель 4 x 4
A B
4
4
x
8
P
A3
A2
B0
B1
A0
B0
B2
A3B0 A2B0 A1B0 A0B0
A3B1 A2B1 A1B1 A0B1
A3B2 A2B2 A1B2 A0B2
B3
x
+
P7
A3
B3
A2
B2
A3B3 A2B3 A1B3 A0B3
P6 P5 P4 P3 P2
A1
B1
P1
A1
A0
0
0
0
0
P0
P7
P6
P5
P4
Глава 5 <36>
P3
P2
P1
P0

37.

Делитель 4 x 4
0
B3
0
B2
0
B1
A3
B0
Legend
R
1
Q3
Q2
A1
1
Q1
A0
1
Q0
R2
R1
R0
+
D
0
N
1
R3
Cout
1
A2
R
B
Cout Cin
D
N R'
B
R'
A/B = Q + R/B
Алгоритм:
R’ = 0
for i = N-1 to 0
R = {R’ << 1. Ai}
D=R-B
if D < 0, Qi=0, R’=R
else
Qi=1, R’=D
R’=R
Глава 5 <37>
Cin

38.

Системы счисления
• Числа можно представить с помощью
двоичного представления
– Положительные числа
• Беззнаковое двоичное
– Отрицательные числа
• Дополнительный код
• Прямой код
• А как же дробные числа?
Глава 5 <38>

39.

Дробные числа
• Две основных способа представления:
– Fixed-point: двоичное число с фиксированной
точкой
– Floating-point: двоичное число с плавающей
точкой – двоичная точка «плавает» между
значащими цифрами
Глава 5 <39>

40.

Числа с фиксированной точкой
• 6.75 содержит 4 разряда целой части и 4
разряда дробной части :
01101100
0110.1100
2
1
-1
-2
2 + 2 + 2 + 2 = 6.75
• В определенном месте подразумевается наличие
двоичной точки
• Количество разрядов целой и дробной части
должно быть определено заранее
Глава 5 <40>

41.

Пример числа с фиксированной точкой
• Представить 7.510 используя 4 целых бита
и 4 дробных.
Глава 5 <41>

42.

Пример числа с фиксированной точкой
• Представить 7.510 используя 4 целых бита
и 4 дробных.
01111000
Глава 5 <42>

43.

Знаковые числа с фиксированной точкой
• Представление:
– Прямой код (знак/величина)
– Дополнительный код (дополнение до основания системы
счисления)
• Пример: Представить -7.510 используя 4 целых и 4
дробных бита
– Прямой код:
– Дополнительный код:
Глава 5 <43>

44.

Знаковые числа с фиксированной точкой
• Представление:
– Прямой код (знак/величина)
– Дополнительный код (дополнение до основания системы
счисления)
• Пример: Представить -7.510 используя 4 целых и 4
дробных бита
– Прямой код:
11111000
– Дополнительный код:
1. +7.5:
01111000
2. Инвертировать значения разрядов: 10000111
3. Добавить 1 к младшему разряду: +
1
10001000
Глава 5 <44>

45.

Числа с плавающей точкой
• Двоичная точка «плавает» между значащими цифрами
• Подобно десятичному представлению в
экспоненциальном представлении
• Например, записать 27310 в экспоненциальном
представлении :
273 = 2.73 × 102
• В общем виде, число записывается в экспоненциальном
представлении как:
± M × BE
–
–
–
–
M = мантисса
B = основание показательной функции
E = порядок (экспонента)
Например, M = 2.73, B = 10, and E = 2
Глава 5 <45>

46.

Числа с плавающей точкой
1 bit
8 bits
23 bits
Sign
Exponent
Mantissa
• Пример: представить число 22810 используя 32-битное
представление с плавающей точкой
Рассмотрим 3 версии – последняя версия
называется IEEE 754 floating-point standard
Глава 5 <46>

47.

Представление с плавающей точкой. 1
1. Преобразовать десятичное в двоичное (не меняйте
местами шаги 1 & 2!):
22810 = 111001002
2. Записать число в двоичной системе и экспоненциальном
представлении:
111001002 = 1.110012 × 27
3. Заполнить каждое поле 32-битное числа с плавающей
точкой:
– Знак – положительный, знаковый бит – (0)
– 8 разрядов порядка представляют значение 7
– Остальные 23 разряда – мантисса
1 bit
0
Sign
8 bits
00000111
Exponent
23 bits
11 1001 0000 0000 0000 0000
Mantissa
Глава 5 <47>

48.

Представление с плавающей точкой. 2
• Первый разряд мантиссы – всегда 1:
– 22810 = 111001002 = 1.11001 × 27
• Следовательно, нет необходимости хранить его: неявная
ведущая 1
• Хранить только дробные разряды мантиссы в 23разрядном поле
1 bit
0
Sign
8 bits
00000111
Exponent
23 bits
110 0100 0000 0000 0000 0000
Fraction
Глава 5 <48>

49.

Представление с плавающей точкой. 3
• Смещенный порядок: смещение = 127 (011111112)
– Смещенный порядок = смещение + порядок
– Порядок 7 хранится как:
127 + 7 = 134 = 0x100001102
• 32-разрядное (IEEE 754) представление с плавающей
точкой числа 22810
1 bit
0
Sign
8 bits
10000110
Biased
Exponent
23 bits
110 0100 0000 0000 0000 0000
Fraction
в 16-ричном коде: 0x43640000
Глава 5 <49>

50.

Представление с плавающей точкой. Пример
Записать число -58.2510 с плавающей точкой (IEEE 754)
Глава 5 <50>

51.

Представление с плавающей точкой. Пример
Записать число -58.2510 с плавающей точкой (IEEE 754)
58.2510 = 111010.012
1.
Записать в двоичной системе и экспоненциальном представлении:
3.
1.1101001 × 25
Заполнить поля:
Знаковый разряд: 1 (отрицательный)
8 разрядов порядка: (127 + 5) = 132 = 100001002
23 разряда мантиссы: 110 1001 0000 0000 0000 0000
1 bit
8 bits
1 100 0010 0
Sign Exponent
23 bits
110 1001 0000 0000 0000 0000
Fraction
в 16-ричном коде: 0xC2690000
Глава 5 <51>

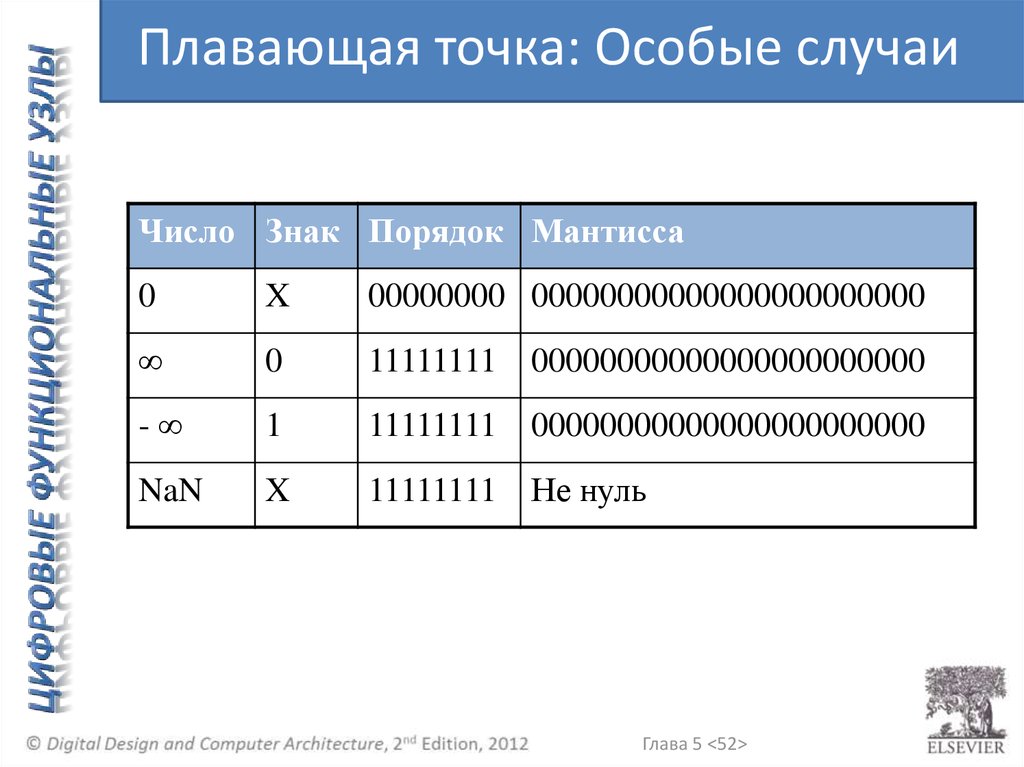
52.

Плавающая точка: Особые случаи
Число Знак Порядок Мантисса
0
X
00000000 00000000000000000000000
∞
0
11111111 00000000000000000000000
-∞
1
11111111 00000000000000000000000
NaN
X
11111111 Не нуль
Глава 5 <52>

53.

Плавающая точка: точность
• Одинарная точность:
– 32-разрядное
– 1 знаковый разряд, 8 разрядов порядка, 23 разряда
мантиссы
– Смещение = 127
• Двойная точность:
– 64- разрядное
– 1 знаковый разряд, 11 разрядов порядка, 52
разряда мантиссы
– Смещение = 1023
Глава 5 <53>

54.

Плавающая точка: округление
• Переполнение: число слишком большое для
представления
• Потеря точности: число слишком маленькое для
представления
• Режимы округления:
– Вниз – к меньшему
– Вверх – к большему
– К нулю (к меньшему по модулю)
– К ближайшему
• Пример: округлить 1.100101 (1.578125) к числу с 3
дробными разрядами
–
–
–
–
Вниз:
Вверх:
К нулю:
К ближайшему:
1.100
1.101
1.100
1.101 (1.625 ближе к 1.578125, чем 1.5)
Глава 5 <54>

55.

Плавающая точка: Суммирование
1.
2.
3.
4.
5.
6.
7.
8.
Выделить порядок числа и мантиссу
Присоединить ведущую 1 к мантиссе
Сравнить порядки
Выполнить сдвиг меньшей мантиссы при
необходимости
Сложить мантиссы
Нормализовать мантиссы и подобрать порядки при
необходимости
Округлить результат
Выполнить сборку порядка и мантиссы обратно в
формат с плавающей точкой
Глава 5 <55>

56.

Суммирование с плавающей точкой. Пример
Сложить числа с плавающей точкой:
0x3FC00000
0x40500000
Глава 5 <56>

57.

Суммирование с плавающей точкой. Пример
1. Извлечь порядок и мантиссу
1 bit
0
Sign
8 bits
01111111
Exponent
23 bits
100 0000 0000 0000 0000 0000
Fraction
1 bit
8 bits
0
10000000
Sign Exponent
23 bits
101 0000 0000 0000 0000 0000
Fraction
Для первого числа (N1):
Для второго числа (N2):
S = 0, E = 127, F = .1
S = 0, E = 128, F = .101
2. Присоединить ведущую 1 к мантиссе
N1:
1.1
N2:
1.101
Глава 5 <57>

58.

Суммирование с плавающей точкой. Пример
3. Сравнить порядки
127 – 128 = -1, поэтому сдвиг N1 вправо на 1 разряд
4. Сдвиг меньшей мантиссы при необходимости
shift N1’s mantissa: 1.1 >> 1 = 0.11 (× 21)
5. Сложить мантиссы
0.11 × 21
+ 1.101 × 21
10.011 × 21
Глава 5 <58>

59.

Суммирование с плавающей точкой. Пример
6. Нормализовать мантиссы и подобрать порядки при
необходимости
10.011 × 21 = 1.0011 × 22
7. Округлить результат
нет необходимости (уложились в 23 разряда)
8. Выполнить сборку порядка и мантиссы обратно в
формат с плавающей точкой
S = 0, E = 2 + 127 = 129 = 100000012, F = 001100..
1 bit
0
Sign
8 bits
10000001
Exponent
23 bits
001 1000 0000 0000 0000 0000
Fraction
Глава 5 <59>

60.

Счетчики
• Инкремент на каждом переднем фронте
• Используется в цикле для перебора всех чисел.
Например,
– 000, 001, 010, 011, 100, 101, 110, 111, 000, 001…
• В примере использованы:
– Отображение цифровых часов
– Программный счетчик: отслеживает выполнение текущей
команды
Symbol
Implementation
CLK
CLK
Q
Reset
+
N
N
1
N
N
N
Q
r
Reset
Глава 5 <60>

61.

Сдвигающий регистр
• Вдвигается новый бит по переднему фронту
тактового сигнала
• Выдвигается бит по переднему фронту тактового
сигнала
• Последовательно-параллельный преобразователь:
преобразует последовательный вход (Sin) в
параллельный выход (Q0:N-1)
Обозначение
Реализация
CLK
Q
Sin Sout
N
Sin
Sout
Q0
Q1
Q2
Глава 5 <61>
QN-1

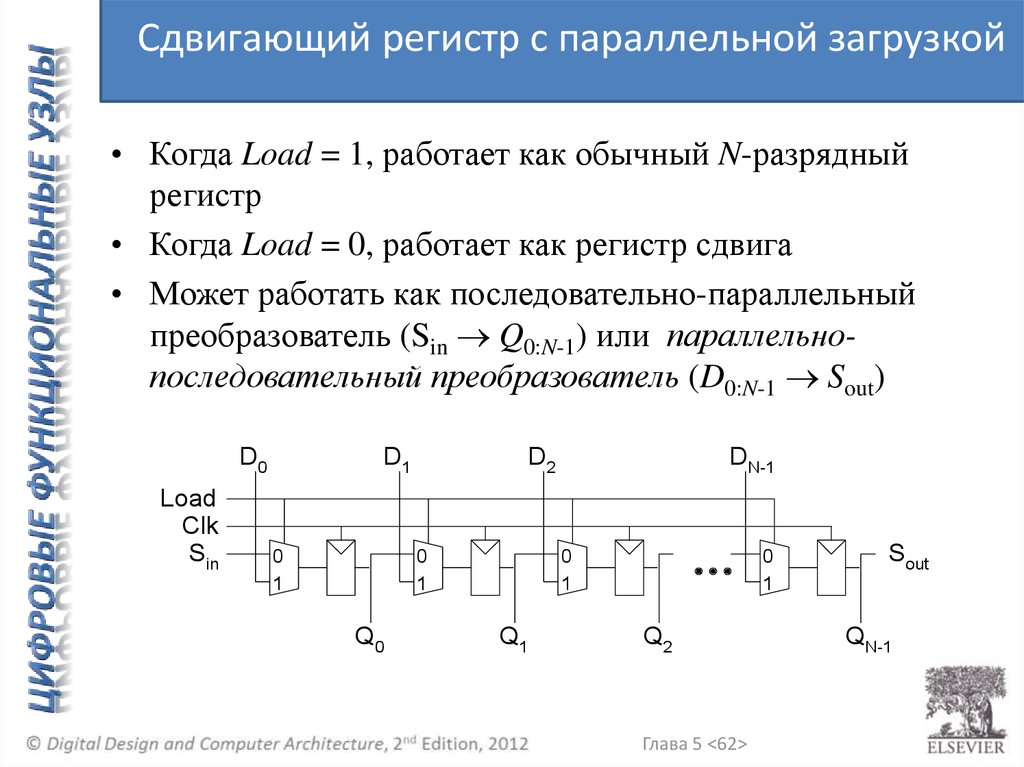
62.

Сдвигающий регистр с параллельной загрузкой
• Когда Load = 1, работает как обычный N-разрядный
регистр
• Когда Load = 0, работает как регистр сдвига
• Может работать как последовательно-параллельный
преобразователь (Sin Q0:N-1) или параллельнопоследовательный преобразователь (D0:N-1 Sout)
D0
Load
Clk
Sin
D1
D2
DN-1
0
0
0
0
1
1
1
1
Q0
Q1
Q2
Глава 5 <62>
Sout
QN-1

63.

Матрицы памяти
• Эффективно хранят большие объемы данных
• 3 основных типа:
– Динамическое оперативное запоминающее устройство (ОЗУ) (DRAM)
– Статическое оперативное запоминающее устройство (ОЗУ) (SRAM)
– Постоянное запоминающее устройство (ПЗУ), память только для чтения
(ROM)
• M-разрядное значение данных считывается/записывается по
уникальному N-разрядному адресу
Address
N
Array
M
Data
Глава 5 <63>

64.

Матрицы памяти
• 2-мерная матрица битовых ячеек
• Каждая битовая ячейка хранит 1 бит
• N адресных битов и M битов данных:
–
–
–
–
Address
N
2N строк и M столбцов
Глубина (Depth): количество строк (количество слов)
Ширина (Width): число столбцов (размер, длина слова)
Размер матрица: depth × width = 2N × M
Address Data
Address
2
Array
3
Data
11
0 1 0
10
1 0 0
01
1 1 0
00
0 1 1
depth
width
Глава 5 <64>
Array
M
Data

65.

Пример матрицы памяти
22 × 3-битовая матрица
Количество слов: 4
Длина слова: 3 бита
Например, 3-битовое слово 100 хранится по адресу 10
Address Data
Address
2
Array
3
Data
11
0 1 0
10
1 0 0
01
1 1 0
00
0 1 1
width
Глава 5 <65>
depth

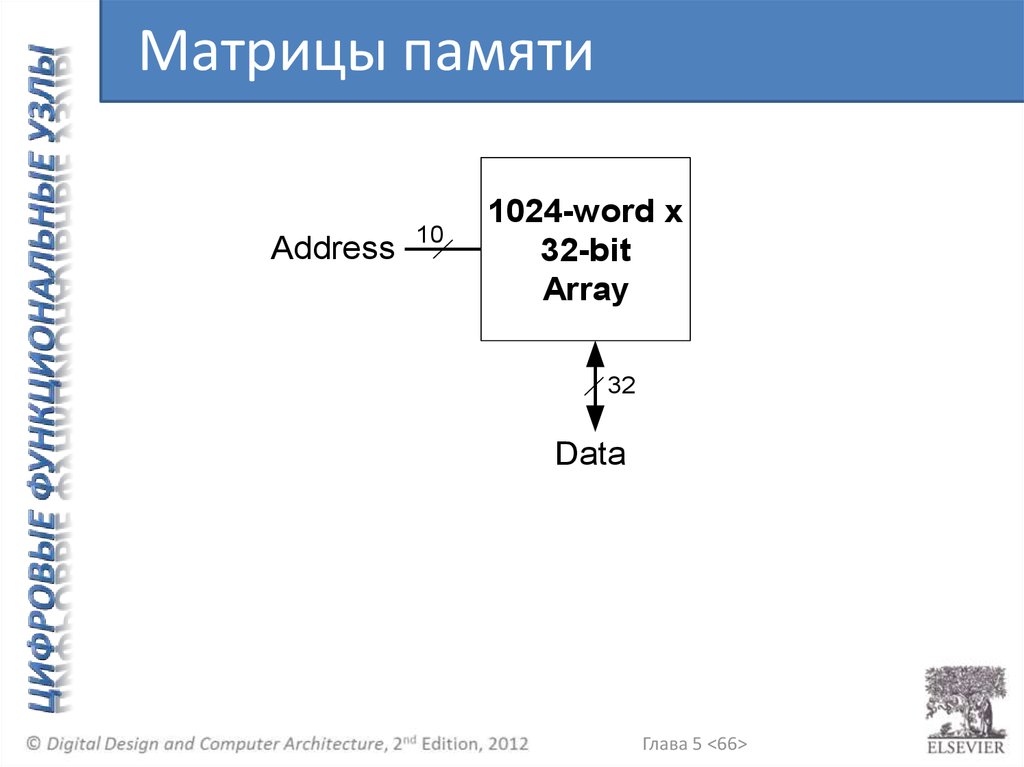
66.

Матрицы памяти
Address
10
1024-word x
32-bit
Array
32
Data
Глава 5 <66>

67.

Запоминающие элементы матрицы памяти
bitline
wordline
stored
bit
bitline =
wordline = 1
bitline =
wordline = 0
stored
bit = 0
stored
bit = 0
bitline =
wordline = 1
bitline =
wordline = 0
stored
bit = 1
(a)
stored
bit = 1
(b)
Глава 5 <67>
Z

68.

Запоминающие элементы матрицы памяти
bitline
wordline
stored
bit
bitline =
wordline = 1
0
bitline =
Z
bitline =
Z
wordline = 0
stored
bit = 0
stored
bit = 0
bitline =
wordline = 1
1
wordline = 0
stored
bit = 1
(a)
stored
bit = 1
(b)
Глава 5 <68>

69.

Матрица памяти
• Линия выборки слов (worldline):
–
–
–
–
формирует сигнал разрешения для выбора строки
в матрице памяти только одна строка может читаться/записываться
соответствует уникальному адресу
только одна линия выборки слов может быть активна
2:4
Decoder
11
Address
2
10
01
00
bitline2
wordline3
wordline2
wordline1
wordline0
bitline1
stored
bit = 0
stored
bit = 1
stored
bit = 0
stored
bit = 1
stored
bit = 0
stored
bit = 0
stored
bit = 1
stored
bit = 1
stored
bit = 0
stored
bit = 0
stored
bit = 1
stored
bit = 1
Data2
Data1
Глава 5 <69>
bitline0
Data0

70.

Типы памяти
• с произвольным доступом, оперативная
память (RAM, ОЗУ): энергозависимая
(volatile)
• Память только для чтения (ROM, ПЗУ):
энергонезависимая (nonvolatile)
Глава 5 <70>

71.

RAM, ОЗУ: оперативная память
• Энергозависимая: содержимое памяти
теряется при отключении электропитания
• Быстрые чтение и запись
• Основная память в компьютере – RAM
(DRAM)
Исторически сложилось название «память с
произвольным доступом», так как в ней доступ к любому
слову данных для чтения или записи осуществляется
всегда за одно и то же время (в отличие от памяти с
последовательным доступом, такой, например, как
магнитная лента)
Глава 5 <71>

72.

ROM, ПЗУ: Память только для чтения
• Энергонезависимая: содержимое памяти
сохраняется при отключении
электропитания
• Чтение быстрое, но запись невозможна
или медленная
• Флэш память в видеокамерах, флэшнакопителях – ROM
Исторически сложилось название «память только для чтения,ROM»,
поскольку информация в нее могла быть записана только во время ее
производства или путем пережигания плавких перемычек. После того,
как память была сконфигурирована, она не могла быть записана снова.
Теперь это уже не так.
Глава 5 <72>

73.

Типы RAM
• DRAM (динамическое ОЗУ - Dynamic
random access memory)
• SRAM (Статическое ОЗУ - Static random
access memory)
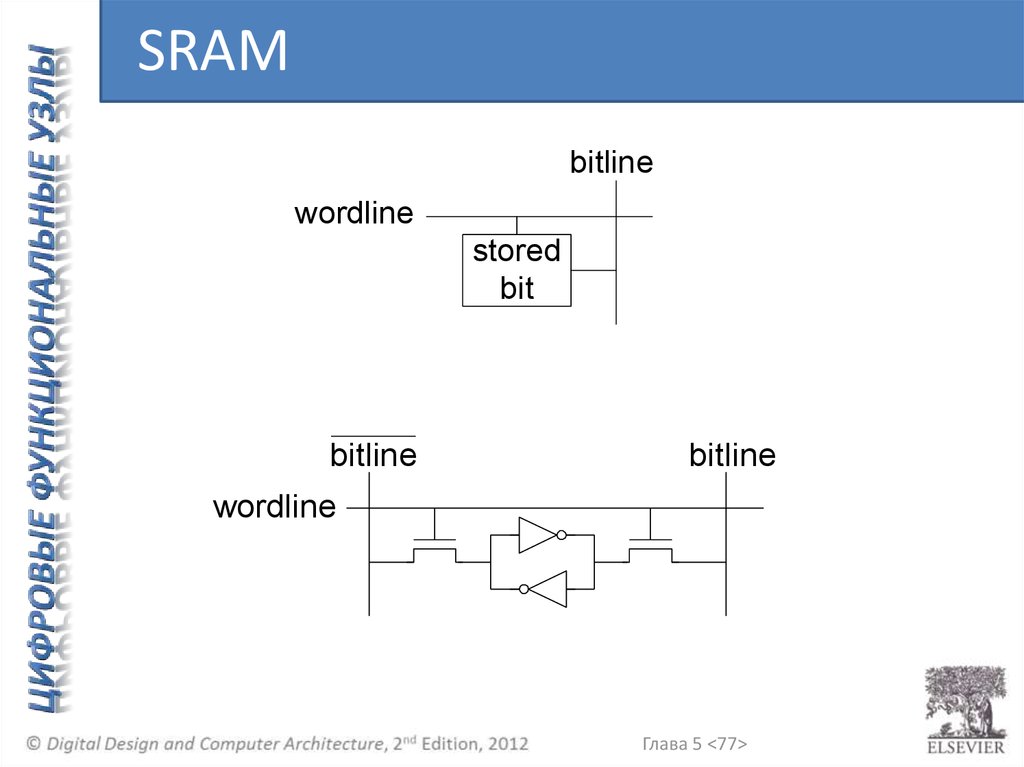
• Отличаются способом хранения данных:
– DRAM использует конденсатор
– SRAM использует инверторы с перекрёстными
обратными связями
Глава 5 <73>

74.

Роберт Деннард, 1932 • Изобрел DRAM в 1966,
IBM
• Многие были настроены
скептически к
работоспособности его
идеи
• С середины 1970-х
DRAM используется
практически во всех
компьютерах
Глава 5 <74>

75.

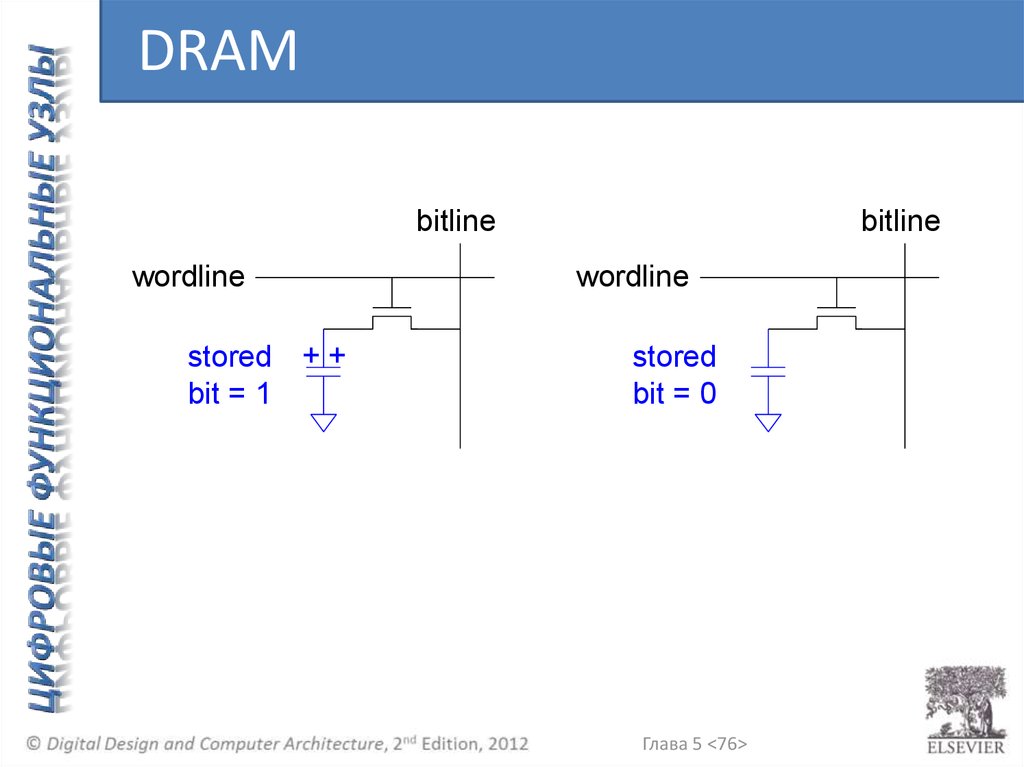
DRAM
• Биты данных сохраняются в конденсаторах
• Динамическая, потому что значение должно быть
обновлено (перезаписано) как периодически, так и
после считывания:
– Утечка заряда конденсатора разрушает значение
– Чтение уничтожает сохраненное значение
bitline
bitline
wordline
wordline
stored
bit
stored
bit
Глава 5 <75>

76.

DRAM
bitline
wordline
stored + +
bit = 1
bitline
wordline
stored
bit = 0
Глава 5 <76>

77.

SRAM
bitline
wordline
stored
bit
bitline
bitline
wordline
Глава 5 <77>

78.

Матрицы памяти. Обзор
2:4
Decoder
11
Address
wordline3
2
10
01
00
bitline2
wordline2
wordline1
wordline0
stored
bit = 0
stored
bit = 1
stored
bit = 0
stored
bit = 1
stored
bit = 0
stored
bit = 0
stored
bit = 1
stored
bit = 1
stored
bit = 0
stored
bit = 0
stored
bit = 1
stored
bit = 1
Data2
DRAM bit cell:
bitline
wordline
bitline1
bitline0
Data1
Data0
SRAM bit cell:
bitline
bitline
wordline
Глава 5 <78>

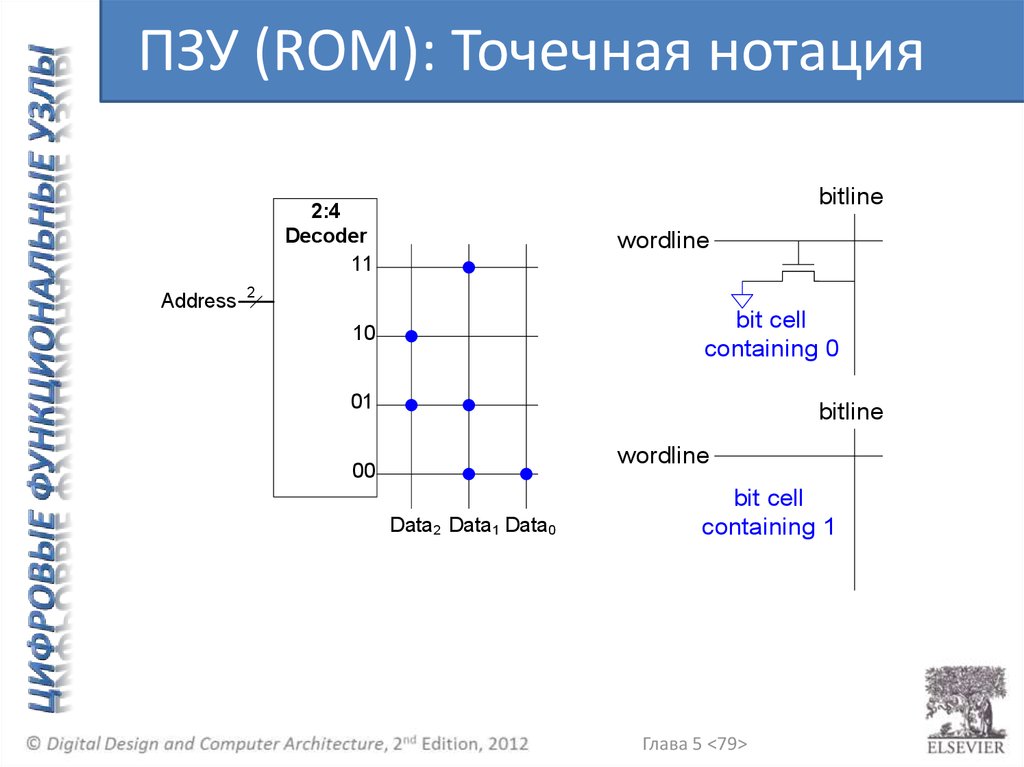
79.

ПЗУ (ROM): Точечная нотация
bitline
2:4
Decoder
11
Address
wordline
2
bit cell
containing 0
10
01
bitline
wordline
00
Data2 Data1 Data0
bit cell
containing 1
Глава 5 <79>

80.

Фуджио Масуока, 1944 • Разрабатывал память и
быстродействующие схемы для
Toshiba, 1971-1994
• Изобрел флэш-память в процессе
самостоятельной работы,
проводимой по ночам и в
выходные дни в конце 1970-х
• Процесс стирания памяти
напомнил ему о вспышке камеры
• Toshiba медленно
коммерциализировала идею; Intel
была первой на рынке в 1988
• Рынок флэш-памяти растет на $ 25
млрд в год
Глава 5 <80>

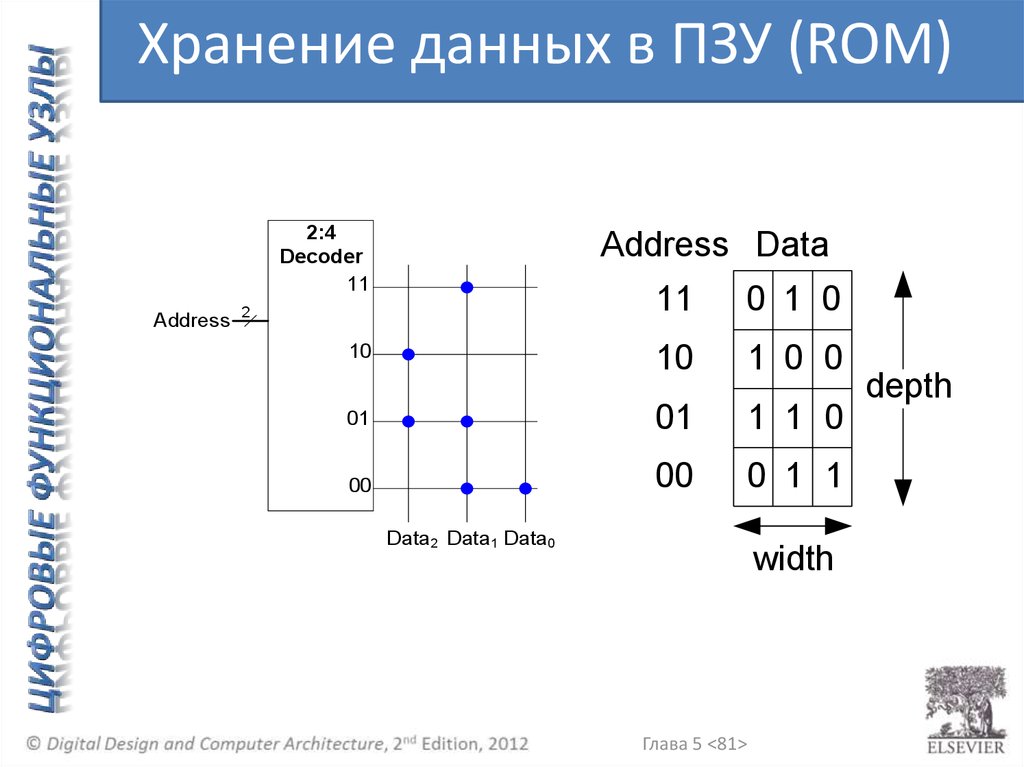
81.

Хранение данных в ПЗУ (ROM)
2:4
Decoder
11
Address
Address Data
11
0 1 0
10
1 0 0
01
01
1 1 0
00
00
0 1 1
2
10
Data2 Data1 Data0
width
Глава 5 <81>
depth

82.

Логические функции и ПЗУ (ROM)
2:4
Decoder
11
Address
Data2 = A1 A0
2
10
Data1 = A1 + A0
01
Data0 = A1A0
00
Data2 Data1 Data0
Глава 5 <82>

83.

Пример: Логика на основе ПЗУ
Реализовать следующие логические функции, используя
ПЗУ 22 × 3-бит:
– X = AB
– Y=A+B
– Z=AB
2:4
Decoder
11
A, B
2
10
01
00
X
Глава 5 <83>
Y
Z

84.

Пример: Логика на основе ROM
Реализовать следующие логические функции, используя
ПЗУ 22 × 3-бит:
– X = AB
– Y=A+B
– Z=AB
2:4
Decoder
11
A, B
2
10
01
00
X
Глава 5 <84>
Y
Z

85.

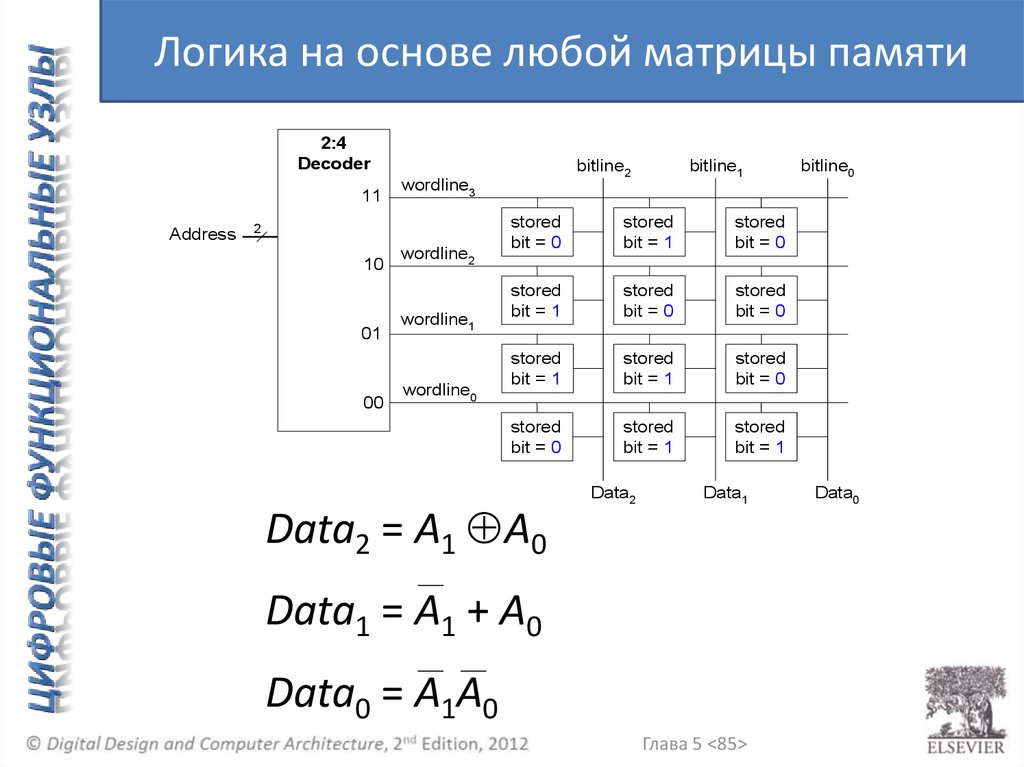
Логика на основе любой матрицы памяти
2:4
Decoder
11
Address
2
10
01
00
bitline2
wordline3
wordline2
wordline1
wordline0
bitline1
stored
bit = 0
stored
bit = 1
stored
bit = 0
stored
bit = 1
stored
bit = 0
stored
bit = 0
stored
bit = 1
stored
bit = 1
stored
bit = 0
stored
bit = 0
stored
bit = 1
stored
bit = 1
Data2 = A1 A0
Data2
Data1
Data1 = A1 + A0
Data0 = A1A0
Глава 5 <85>
bitline0
Data0

86.

Логика на основе матрицы памяти
Реализовать следующие логические функции, используя
22 × 3-битовую матрицу памяти:
– X = AB
– Y=A+B
– Z=AB
Глава 5 <86>

87.

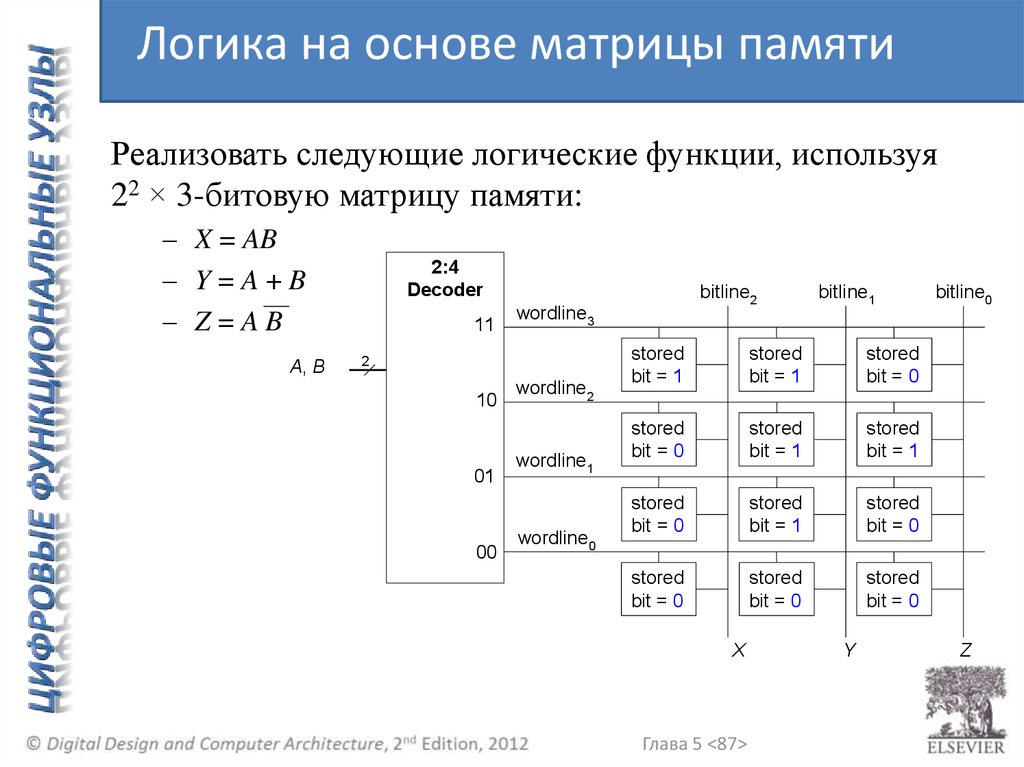
Логика на основе матрицы памяти
Реализовать следующие логические функции, используя
22 × 3-битовую матрицу памяти:
– X = AB
– Y=A+B
– Z=AB
A, B
2:4
Decoder
11
wordline3
2
10
01
00
bitline2
wordline2
wordline1
wordline0
bitline1
stored
bit = 1
stored
bit = 1
stored
bit = 0
stored
bit = 0
stored
bit = 1
stored
bit = 1
stored
bit = 0
stored
bit = 1
stored
bit = 0
stored
bit = 0
stored
bit = 0
stored
bit = 0
X
Глава 5 <87>
Y
bitline0
Z

88.

Логика на основе матрицы памяти
Таблицы преобразования (lookup tables, LUTs), каждой
входной комбинации соответствует некоторое состояние
выхода
4-word x 1-bit Array
2:4
Decoder
00
Truth
Table
A
0
0
1
1
B
0
1
0
1
Y
0
0
0
1
A
A1
B
A0
bitline
stored
bit = 0
01
stored
bit = 0
10
stored
bit = 0
11
stored
bit = 1
Y
Глава 5 <88>

89.

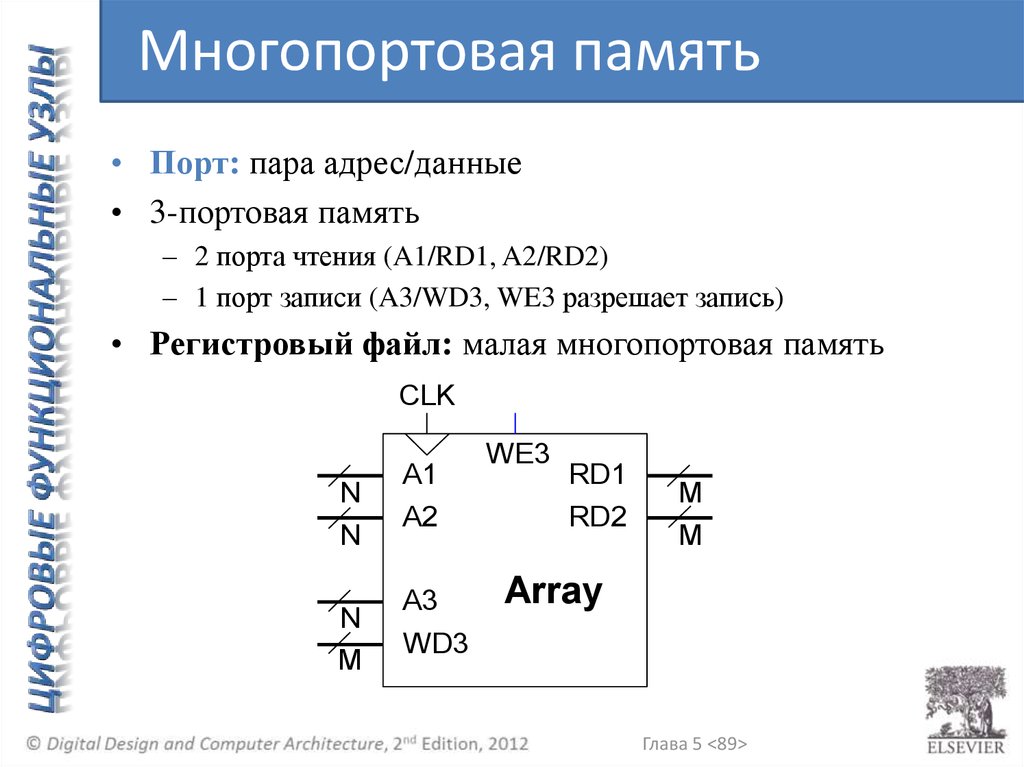
Многопортовая память
• Порт: пара адрес/данные
• 3-портовая память
– 2 порта чтения (A1/RD1, A2/RD2)
– 1 порт записи (A3/WD3, WE3 разрешает запись)
• Регистровый файл: малая многопортовая память
CLK
N
N
N
M
A1
A2
A3
WE3
RD1
RD2
M
M
Array
WD3
Глава 5 <89>

90.

SystemVerilog: матрицы памяти
// 256 x 3 модуль памяти с одним портом чтения/записи
module dmem( input logic
clk, we,
input logic[7:0] a
input logic [2:0] wd,
output logic [2:0] rd);
logic
[2:0] RAM[255:0];
assign rd = RAM[a];
always @(posedge clk)
if (we)
RAM[a] <= wd;
endmodule
Глава 5 <90>

91.

Матрицы логических элементов
• PLAs (ПЛМ, Programmable logic arrays) –
программируемая логическая матрица
– AND матрица, затем OR матрица
– Только комбинационная логика
– Фиксированные внутренние соединения
• FPGAs (Field programmable gate arrays) –
Программируемая пользователем матрица
логических элементов
– Массив конфигурируемых логических блоков CLB
– Комбинационная и последовательностная логика
– Программируемые внутренние соединения
Глава 5 <91>

92.

Программируемые логические матрицы
• X = ABC + ABC
Inputs
• Y = AB
M
Implicants
AND
ARRAY
N
OR
ARRAY
P
Outputs
A
B
C
OR ARRAY
ABC
ABC
AB
AND ARRAY
X
Y
Глава 5 <92>

93.

PLA (ПЛМ): Точечная нотация
Inputs
M
AND
ARRAY
Implicants
OR
ARRAY
N
P
A
B
Outputs
C
OR ARRAY
ABC
ABC
AB
AND ARRAY
X
Y
Глава 5 <93>

94.

FPGA: Программируемая пользователем матрица
логических элементов
• Состоит из:
– LE (логических элементов): реализуют логику
– IOE (Элементов ввода/вывода): интерфейс с
внешним миром
– Programmable interconnection:
программируемые соединения связывают
логические элементы с элементами ввода/вывода
– Некоторые FPGAs включают и другие блоки,
такие как умножители и память RAMs
Глава 5 <94>

95.

Обобщенная структура FPGA
Глава 5 <95>

96.

LE: Логические элементы
• Состоят из:
– Таблиц преобразования (LUT): реализуют
комбинационную логику
– Триггеров: реализуют последовательностную
логику
– Мультиплексоров: соединяют таблицы
преобразования (LUT) и триггеры
Глава 5 <96>

97.

Altera Cyclone IV LE
Глава 5 <97>

98.

Altera Cyclone IV LE
• Конфигурируемые логические блоки
(CLB) Spartan имеют:
– 1 четырехвходовую LUT
– 1 регистровый выход
– 1 комбинационный выход
Глава 5 <98>

99.

Конфигурация ЛБ. Пример
Покажите, как сконфигурировать логические блоки Cyclone
IV для выполнения следующих функций:
– X = ABC + ABC
– Y = AB
Глава 5 <99>

100.

Конфигурация ЛБ. Пример
Покажите, как сконфигурировать ЛБ Cyclone IV для
выполнения следующих функций:
– X = ABC + ABC
– Y = AB
(A)
(B)
(C)
data 1 data 2 data 3 data 4
0
0
0
X
0
0
1
X
0
1
0
X
0
1
1
X
1
0
0
X
1
0
1
X
1
1
0
X
1
1
1
X
(A)
(B)
data 1 data 2 data 3 data 4
0
0
X
X
0
1
X
X
1
0
X
X
1
1
X
X
(X)
LUT output
0
1
0
0
0
0
1
0
C
A
B
0
data 1
data 2
data 3
data 4
X
LUT
LE 1
(Y)
LUT output
0
0
1
0
A
B
0
0
data 1
data 2
data 3
data 4
Y
LUT
LE 2
Глава 5 <100>

101.

FPGA. Последовательность проектирования
Используя средства САПР (Altera’s Quartus II):
• Описать проект с использованием редактора
принципиальных схем или HDL
• Выполнить моделирование проекта
• Выполнить синтез проекта и его имплементацию в
FPGA
• Загрузить конфигурацию в FPGA
• Протестировать проект
Глава 5 <101>