Похожие презентации:
Площадь параллелограмма
1. Площадь параллелограмма.
2. Задачи нашего урока
• доказать теорему оплощади
параллелограмма и
вывести следствие из
неё; использовать их
при решении задач.
• Будут выведены формулы,
по которым можно
вычислить площадь
параллелограмма.
• Все эти формулы широко
используются не только при
решении геометрических
задач, но и в обыденной
практике, при различных
расчётах, связанных с
техникой, производством,
конструированием.
3. Математическая разминка (готовимся к ОГЭ)
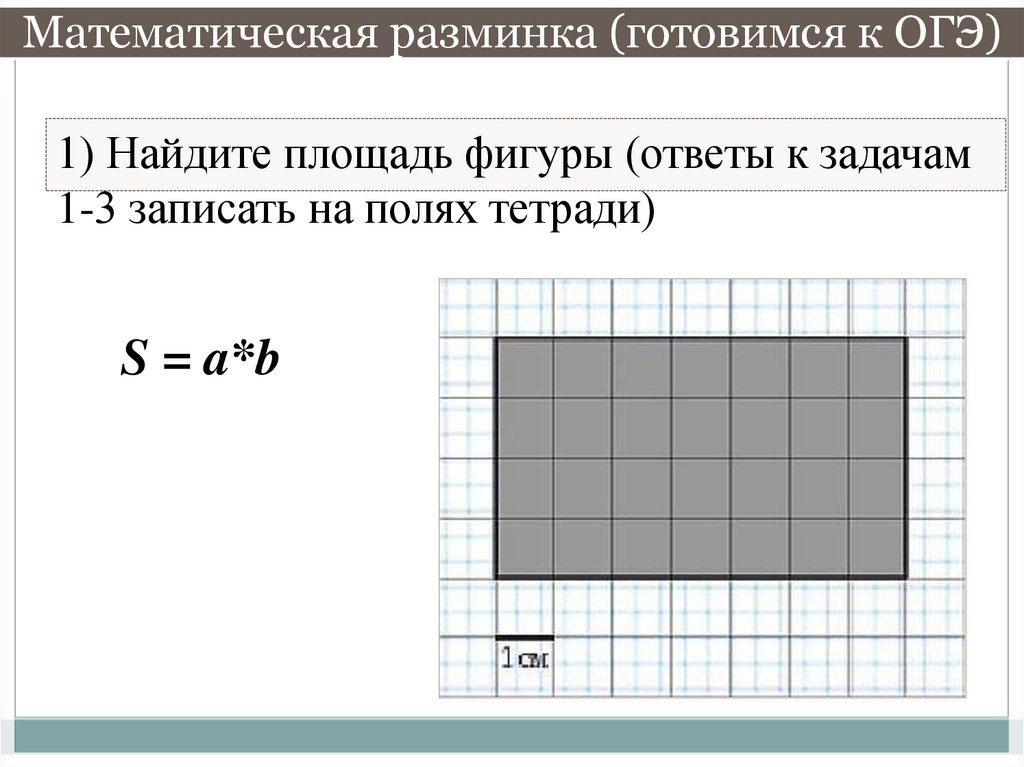
1) Найдите площадь фигуры (ответы к задачам1-3 записать на полях тетради)
S = a*b
4. 2) Периметр квадрата равен 40. Найдите площадь квадрата.
P = 4*aa= ¼*P
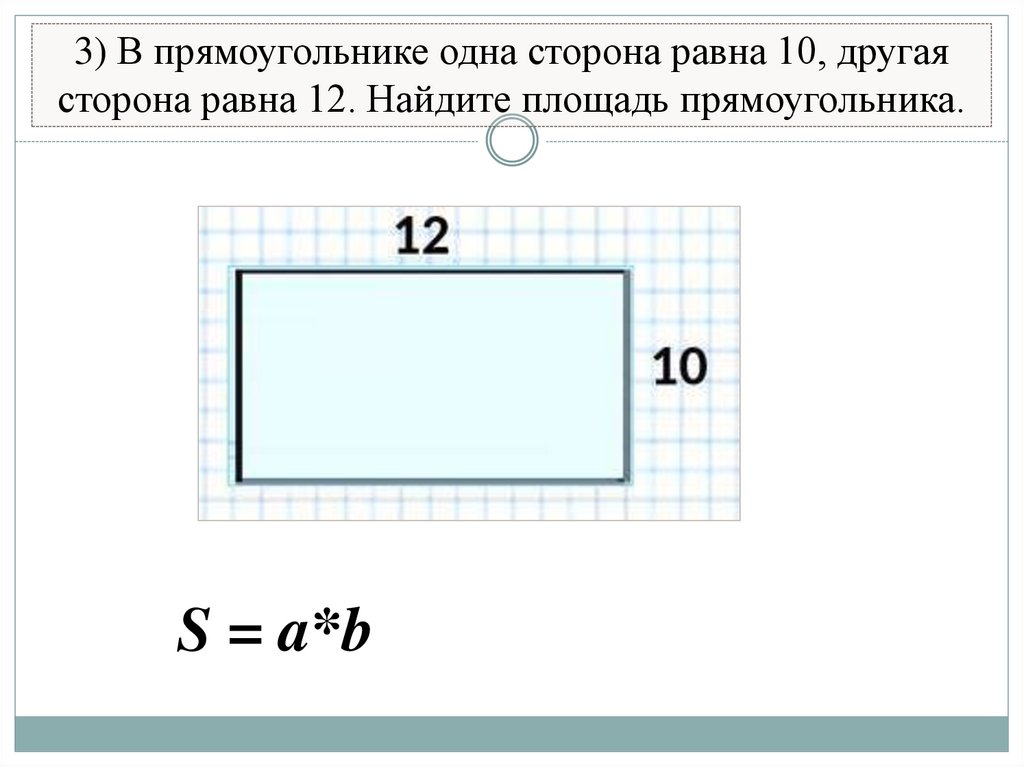
5. 3) В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
3) В прямоугольнике одна сторона равна 10, другаясторона равна 12. Найдите площадь прямоугольника.
S = a*b
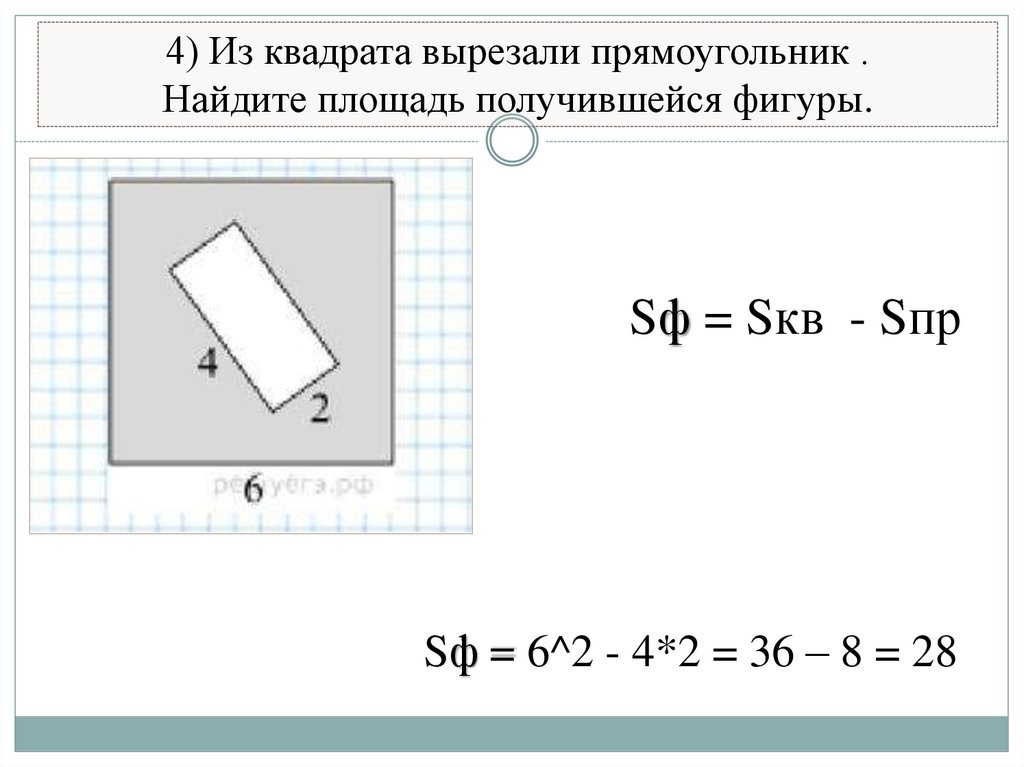
6. 4) Из квадрата вырезали прямоугольник . Найдите площадь получившейся фигуры.
Sф = Sкв - SпрSф = 6^2 - 4*2 = 36 – 8 = 28
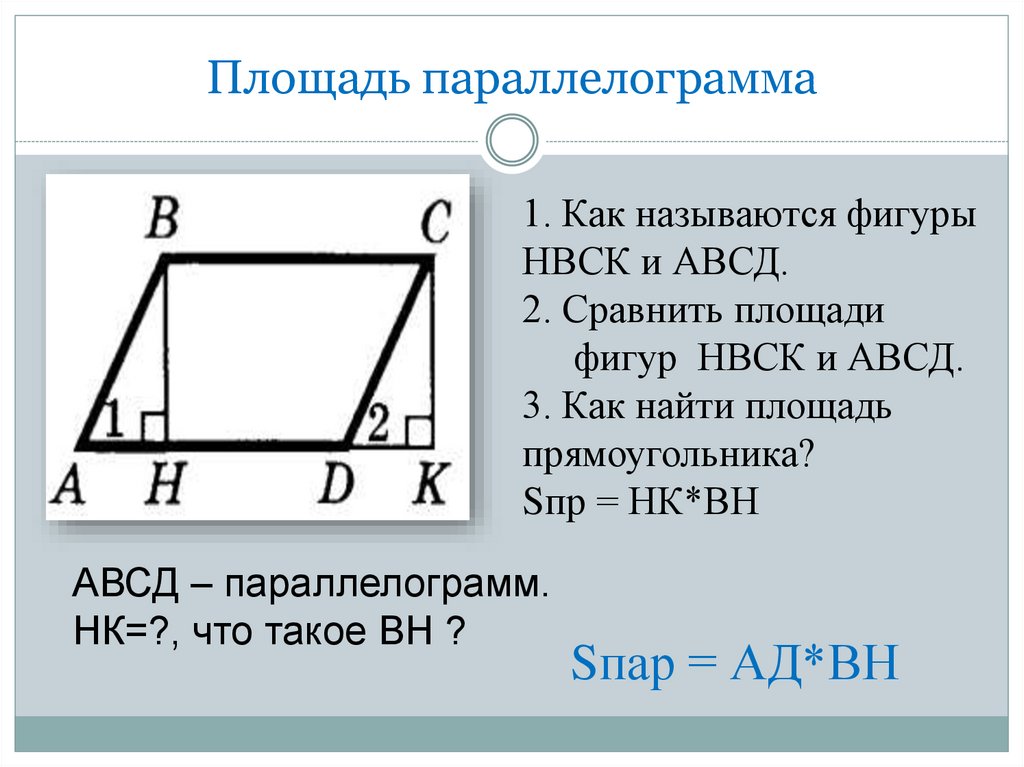
7. Площадь параллелограмма
1. Как называются фигурыНВСК и АВСД.
2. Сравнить площади
фигур НВСК и АВСД.
3. Как найти площадь
прямоугольника?
Sпр = НК*ВН
АВСД – параллелограмм.
НК=?, что такое ВН ?
Sпар = АД*ВН
8. Площадь параллелограмма
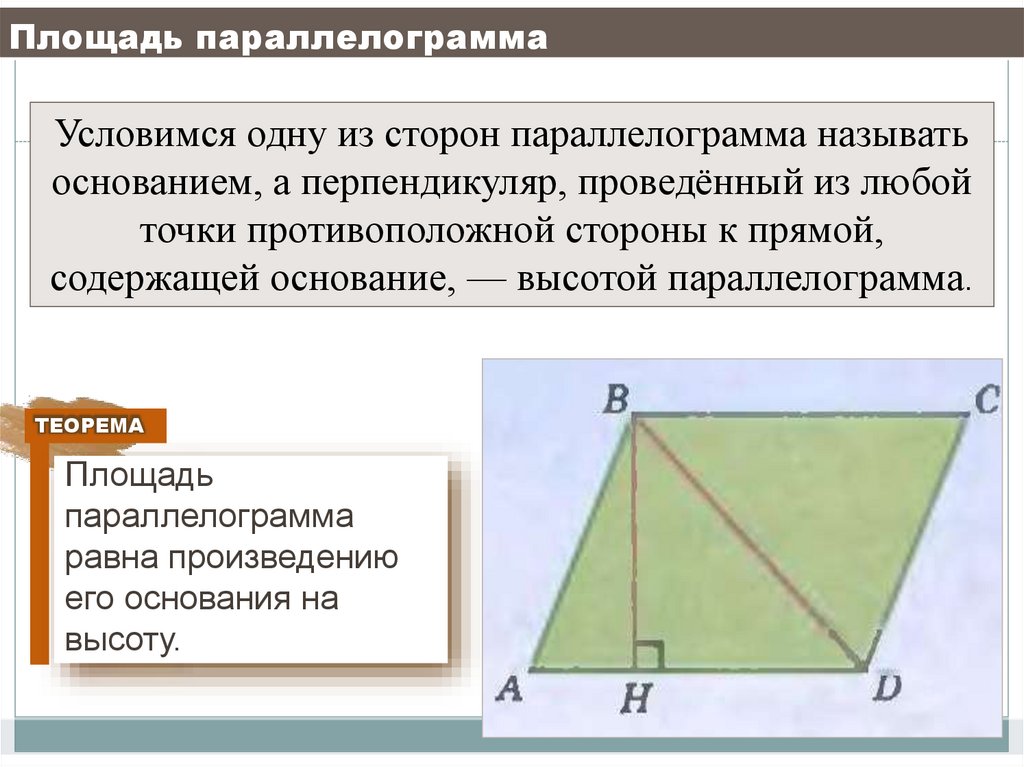
Условимся одну из сторон параллелограмма называтьоснованием, а перпендикуляр, проведённый из любой
точки противоположной стороны к прямой,
содержащей основание, — высотой параллелограмма.
ТЕОРЕМА
Площадь
параллелограмма
равна произведению
его основания на
высоту.
9. Теорема (формула площади параллелограмма по стороне и высоте)
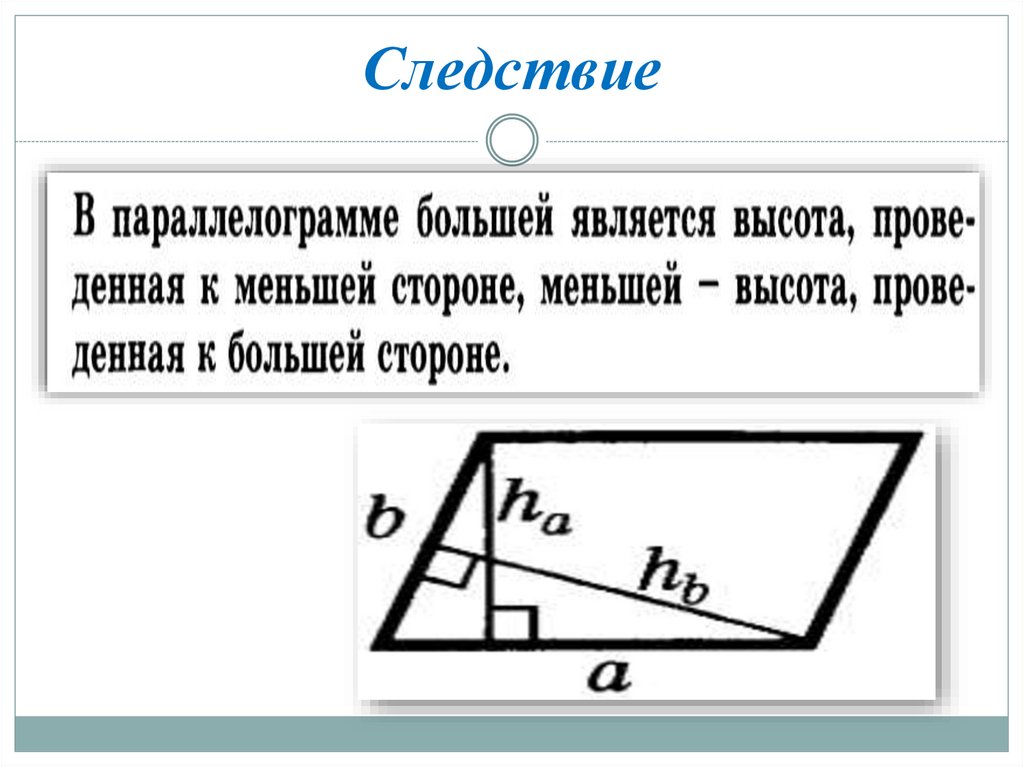
10. Следствие
11. Метод вспомогательных площадей (метод площадей)
12. Повторение материала из 7 класса
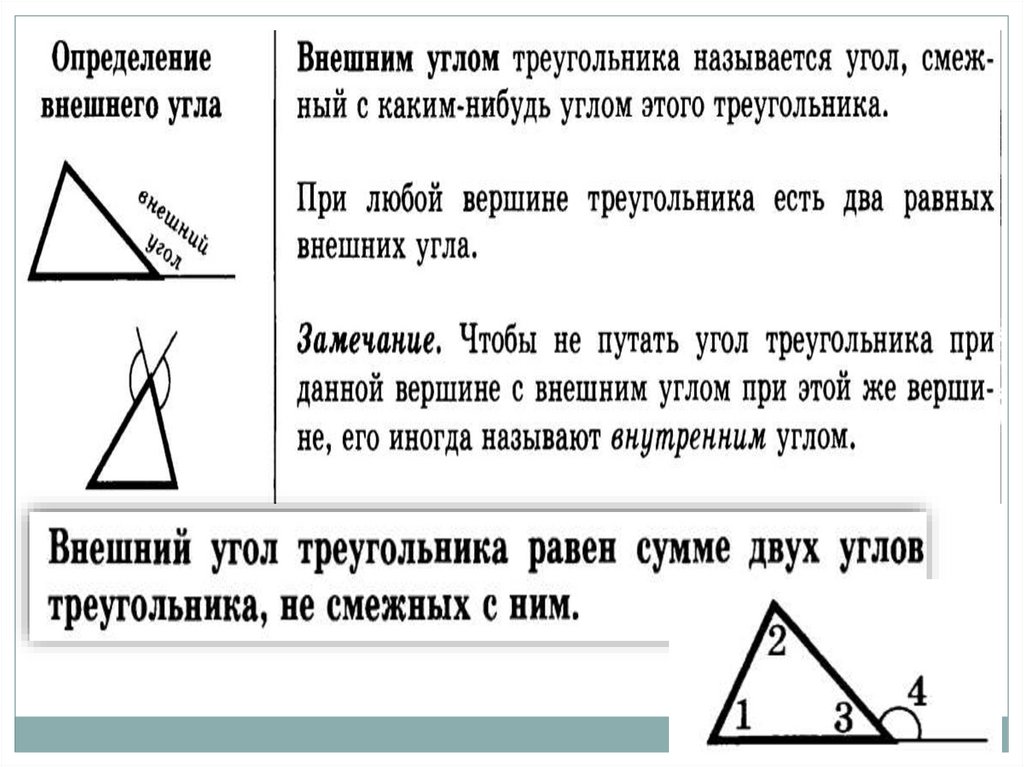
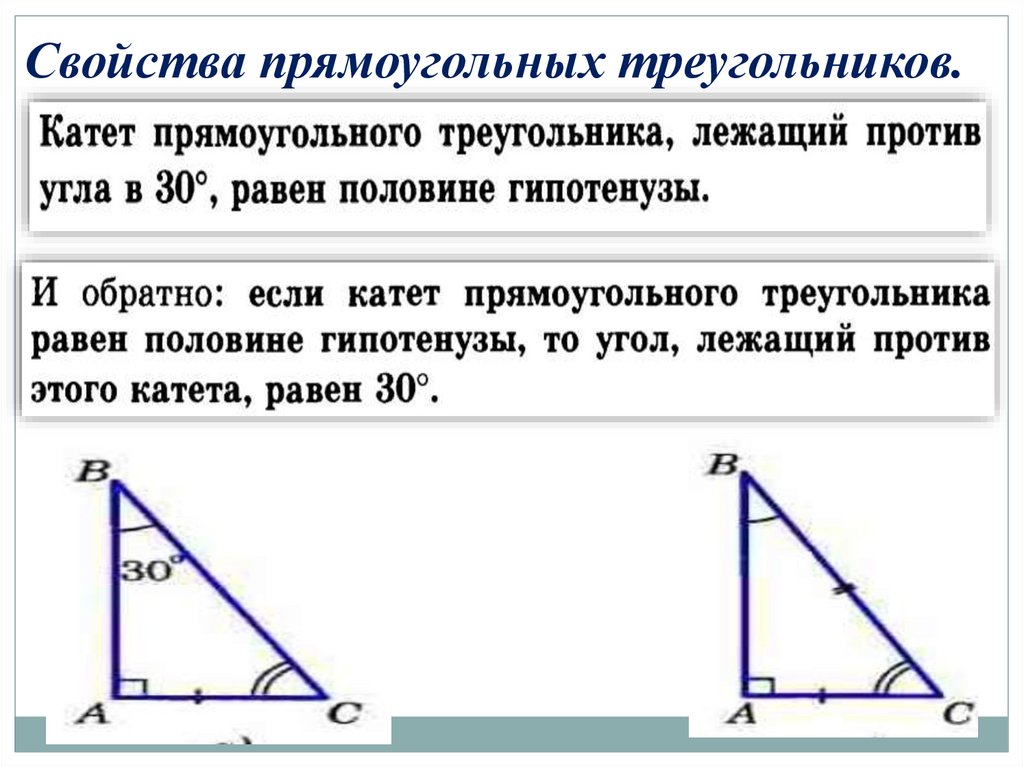
1. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.2. СООТНОШЕНИЯ СТОРОН В
ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ












 Математика
Математика








