Похожие презентации:
Применение букв для записи математических выражений и предложений
1.
Применение букв для записиматематических выражений и
предложений
Буквенные выражения
2.
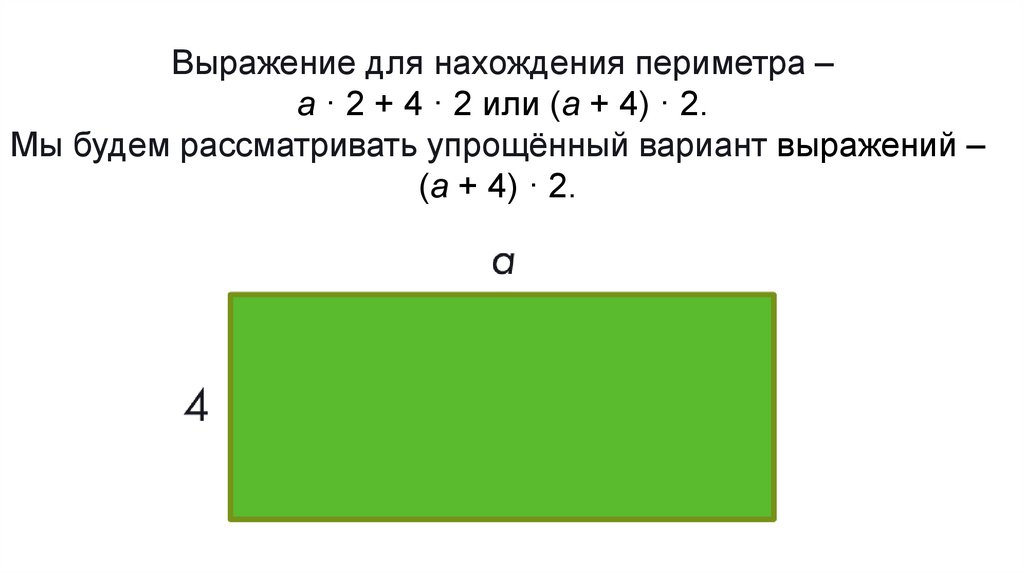
Запиши выражение для нахождения периметра прямоугольникасо сторонами
a см и 4 см.
3.
Выражение для нахождения периметра –a · 2 + 4 · 2 или (a + 4) · 2.
Мы будем рассматривать упрощённый вариант выражений –
(a + 4) · 2.
4.
Для записей выражений используютматематические операции: знаки
арифметических действий, такие, как
умножение, деление, сложение,
вычитание.
5.
Запись (5 + 7) ⋅ 2 – это числовое выражениеВыражения, которые содержат только числа и
математические операции,
называются числовыми выражениями.
Выполним арифметические действия.
(5 + 7) · 2 = 12 · 2 = 24.
Число 24 является значением числового
выражения.
6.
Запись (a + 4) ⋅ 2 – это буквенное выражениеВыражения, которые содержат буквы, числа и
математические операции, называются
буквенными выражениями.
Примеры буквенных выражений:
a ⋅ 3; ab; 5 ⋅ (a – b).
7.
Коэффициент обычно пишут перед буквеннымимножителями:
a ⋅ 3 = 3 ⋅ a;
ab = 1 ⋅ ab;
5 ⋅ (a – b).
Если выражение является произведением числа
и одной или нескольких букв,
то это число называют числовым
коэффициентом (или просто коэффициентом).
Если перед буквой в выражении нет числа, то
коэффициент считаем равным 1.
8.
Степень в буквенном выражении записывается по аналогиисо степенью числового выражения.
Читается «a в третьей степени» или «a в кубе».
9.
Правило 1.Знак умножения в буквенных выражениях
пишут только между числами.
3 ⋅ 27a.
10.
Правило 2.Знак умножения в буквенных выражениях опускается,
если он стоит между буквой и числом.
7 ⋅ a = 7a;
a ⋅ b = ab;
3 ⋅ (a – b) = 3 (a – b).
11.
Правило 3.Знак перед коэффициентом принадлежит
только этому коэффициенту,
а не переменным. В выражении +6
b число +6 – это коэффициент при букве b.
12.
Определим коэффициент в выражении2 ⋅ a ⋅ 3 ⋅ b ⋅ 5.
Перемножим отдельно числа и буквы:
2 ⋅ a ⋅ 3 ⋅ b ⋅ 5 = 2 ⋅ 3 ⋅ 5 ⋅ a ⋅ b = 30 ⋅ ab = 30ab
Коэффициент равен 30.
Чтобы определить коэффициент в выражении, нужно отдельно
перемножить числа, входящие в это выражение,
и отдельно перемножить буквы.
Получившийся числовой сомножитель и будет коэффициентом.
13.
Пример 1. 5a + 7b + 11a.Слагаемые 5a и 11a являются подобными.
Подобные слагаемые – это слагаемые, которые имеют одинаковую
буквенную часть. Например, рассмотрим выражение 5a + 7b + 11a.
Слагаемые 5a и 11a имеют одинаковую буквенную часть – переменную a.
Значит, слагаемые 5a и 11a являются подобными.
14.
Пример 2. Привести подобные слагаемые в выражении 13a + 24a – 15a.В данном случае подобными являются все слагаемые.
Сложим их коэффициенты и результат
умножим на общую буквенную часть – на переменную a:
13a + 24a – 15a = (13 + 24 – 15) ⋅ a = 22a.
15.
13a + 24a – 15a = (13 + 24 – 15) ⋅ a = 22a.Рассмотрим задание на приведение подобных слагаемых.
Обычно подобные слагаемые складывают
(вычитают), чтобы упростить выражение.
Это действие называют приведением подобных слагаемых.
Чтобы привести подобные слагаемые,
нужно сложить (вычесть) коэффициенты
этих слагаемых и полученный результат умножить
на общую буквенную часть.
Подобные слагаемые обычно приводят
в уме и результат записывают сразу.
16.
17.
Как читаются буквенные выражения?18.
Как читаются буквенные выражения?19.
20.
ДОМАШНЕЕ ЗАДАНИЕ1. Составить буквенное выражение:
а)разность удвоенного числа x и числа b;
б)частное числа 25 и суммы чисел m и p;
в)разность числа 45 и утроенного числа k;
г)произведение числа 15 и суммы чисел n и d.
2. https://learningapps.org/view7234891
3. https://learningapps.org/view14369630














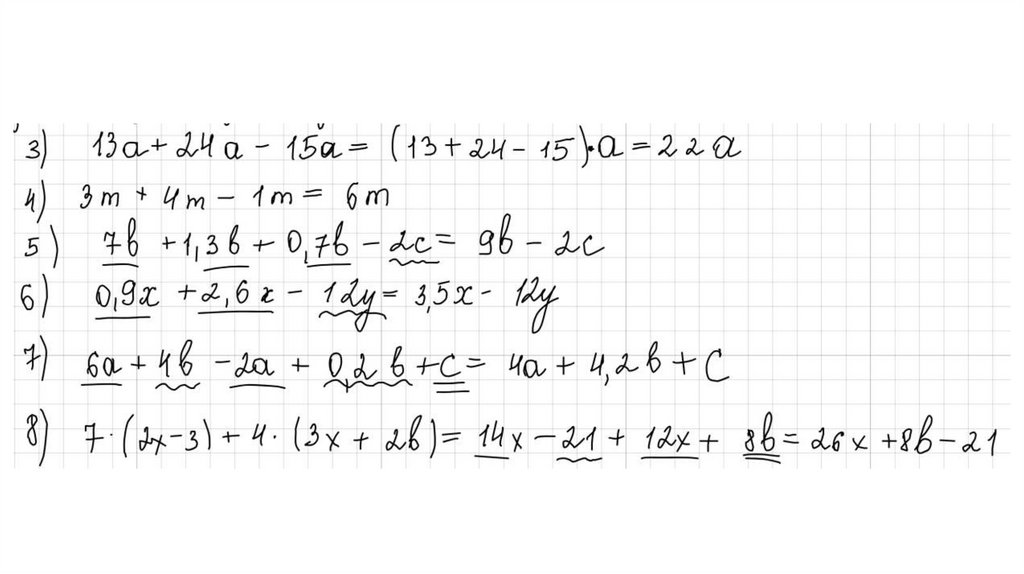




 Математика
Математика








