Определение перемещений в балке аналитическим способом (лекция 1)

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра Строительной механики
Лекция 1.
Определение перемещений в балке аналитическим способом.
Авторы:
к.т.н., Войтко Александр Михайлович
1

2.

Вертикальное перемещение произвольной точки оси балки, то есть перемещение
вдоль оси z , будем называть прогибом и обозначать w(х). Угол поворота
произвольного сечения обозначим φ(х)
Функции w(х) и φ(х) связаны между собой следующей зависимостью:
(4.14)
Для балок условием жесткости является условие, ограничивающее
максимальный прогиб, т. е.
(4.15)
где [w] – допускаемый прогиб, который задается в долях от длины пролета
балки l и в зависимости от типа проектируемой конструкции может находиться
в пределах от l/300-200 (для перекрытий жилых зданий) до l/1000 (для
промышленных зданий, где крепится промышленное оборудование .
2

3.

Деформации балок при изгибе
Рассмотрим два наиболее часто
используемых способа определения
перемещений балок (прогибов и углов
поворота): способ, основанный на
интегрировании приближенного
дифференциального уравнения
изогнутой оси балки, называемый
аналитическим способом и метод
Максвелла
– Мора
Аналитический
способ основан на
интегрировании приближенного
дифференциального уравнения изогнутой
оси балки EIw′′(x) = −M(x) (4.16)
Здесь EI – жесткость балки при изгибе, то
есть произведение модуля упругости на
момент инерции. Предполагается, что эта
величина не меняется по длине балки;
M(x) – изгибающий момент в
произвольном сечении балки.
3

4.

Интегрируя уравнение (4.16), мы получим умноженные на жесткость угол поворота
произвольного сечения
EIw′(x) = −∫ M (x)dx + C
(4.17)
и прогиб произвольного сечения
EIw( x) = −∫ ∫ M ( x)dxdx + Cx + D
(4.18)
В формулах (4.17), (4.18) С и D – произвольные постоянные, которые
находятся из граничных условий, зависящих от условий закрепления балки.
Для каждой статически определимой балки можно записать два граничных
условия для определения двух произвольных постоянных.
Правило знаков для прогиба и угла
поворота
Согласно этому правилу прогиб вниз (по
направлению оси z) считается положительным.
Знак угла поворота зависит от того, где
находится начало отсчета х. Если начало отсчета
х находится слева, как показано на рисунке,
поворот сечения по часовой стрелке считается
4

5.

Правила Клебша
1.Начало координат для всех участков должно быть единым и находиться на конце балки
(левом или правом)(см. рисунок).
2.При составлении выражения для изгибающего момента на каждом участке
рассматриваем всегда все силы с той стороны от сечения, где находится начало
координат.
3. Если на балку действует распределенная нагрузка, которая обрывается в каком-то
сечении балки, то ее следует продолжить до конца балки и приложить на участке, где
добавлена нагрузка, распределенную нагрузку той же интенсивности, но
противоположного знака (см. рисунок). (Конец балки всегда противоположен выбранному
началу координат.)
4.Если к балке приложена сосредоточенная пара сил M0, то в выражение для изгибающего
момента она входит с множителем (x−a)0, где а – расстояние от начала координат до
места приложения
пары сил (см. рисунок).
5. Интегрирование ведется без раскрытия скобок:
5

6.

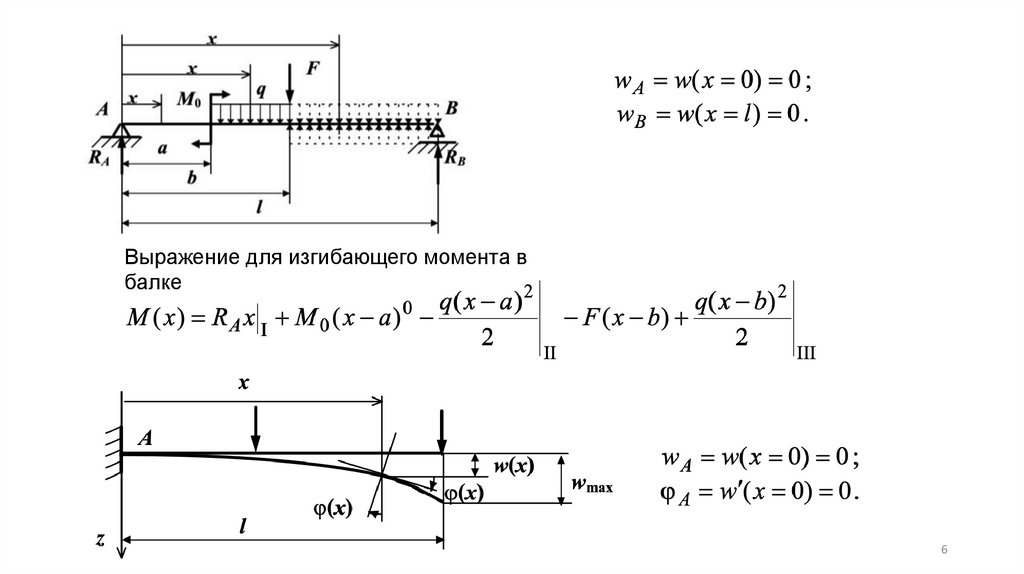
Выражение для изгибающего момента в
балке
6

7.

Для балки с произвольным числом участков при использовании правил Клебша
произвольные постоянные C и D имеют следующий геометрический смысл:
где
соответственно прогиб и угол поворота балки в начале
координат.
7

8.

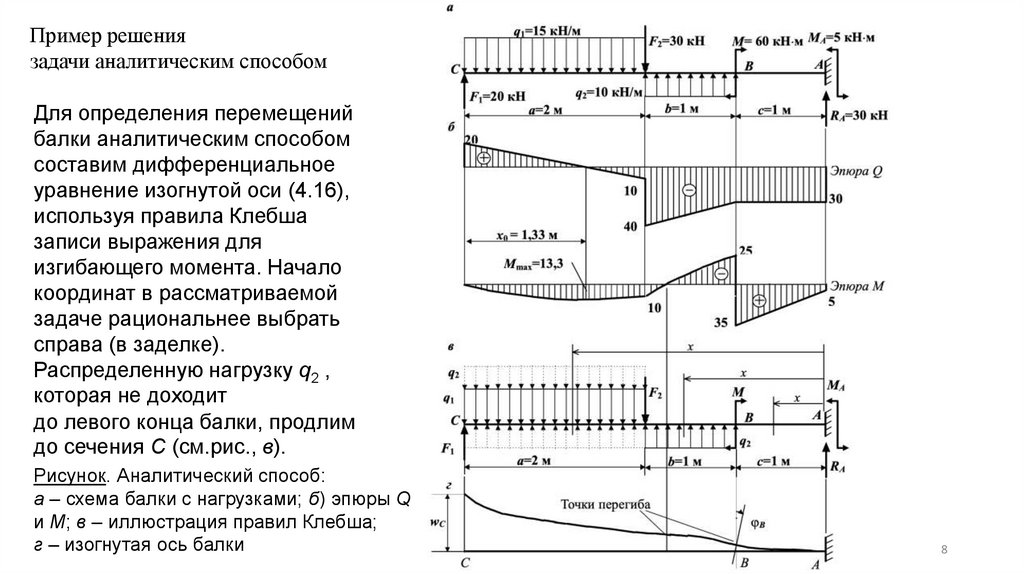
Пример решения
задачи аналитическим способом
Для определения перемещений
балки аналитическим способом
составим дифференциальное
уравнение изогнутой оси (4.16),
используя правила Клебша
записи выражения для
изгибающего момента. Начало
координат в рассматриваемой
задаче рациональнее выбрать
справа (в заделке).
Распределенную нагрузку q2 ,
которая не доходит
до левого конца балки, продлим
до сечения С (см.рис., в).
Рисунок. Аналитический способ:
а – схема балки с нагрузками; б) эпюры Q
и М; в – иллюстрация правил Клебша;
г – изогнутая ось балки
8

9.

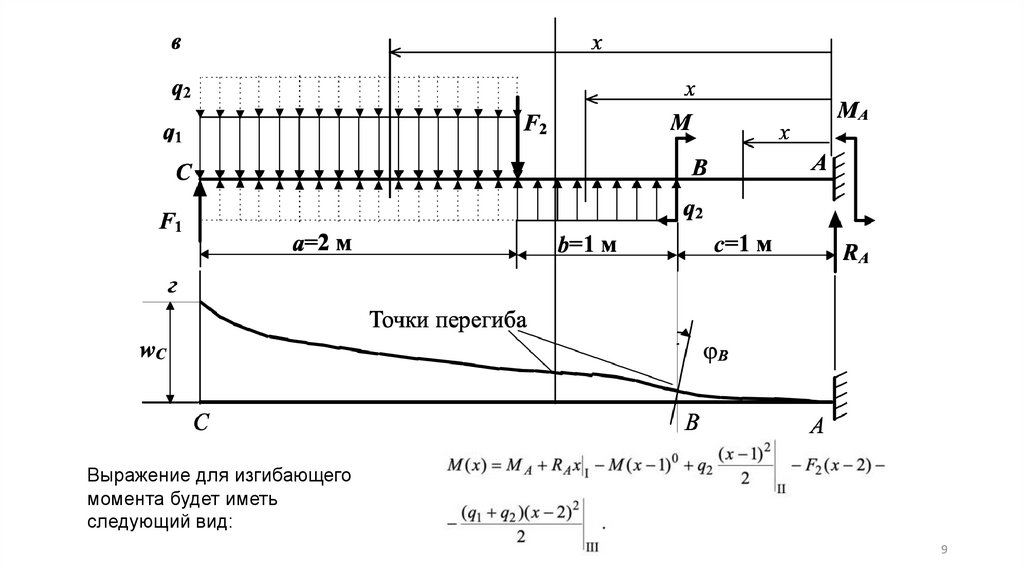
Выражение для изгибающего
момента будет иметь
следующий вид:
9

10.

Подставим это выражение в дифференциальное уравнение (4.16) и проинтегрируем его
два раза:
10

11.

Граничные условия: в заделке (в
сечении А, где находится начало
координат) угол поворота и прогиб
балки равны нулю, т.е.
Для определения угла поворота в сечении В
подставим в выражение для угла по- ворота
на первом участке (только до черты с
номером I) значение x=1м:
В соответствии с правилом знаков
отрицательный знак угла поворота для
выбранного начала координат х справа
означает, что поворот сечения происходит по
часовой стрелке.
11

12.

В сечении С, где требуется найти прогиб, координата х равна 4 м , и это сечение
находится на третьем участке балки, поэтому подставляем х = 4 м в выражение для
прогибов, используя слагаемые на всех трех участках:
Знак минус у найденного прогиба показывает, что сечение С перемещается вверх.
В заключение сосчитаем прогиб балки в сантиметрах, угол поворота в радианах и
проверим условие жесткости. Найдем жесткость ЕI рассматриваемой деревянной
балки из трех бревен радиусом 12 см. Момент инерции поперечного сечения
12

13.

Модуль упругости дерева
Тогда
Прогиб балки в сечении
С:
а угол поворота сечения
В:
Очевидно (см. рис. 4.20, г), что найденный прогиб балки в сечении С является
максимальным, поэтому для проверки условия жесткости сравним его с допускаемым
прогибом. Для балки длиной l=4м допускаемый прогиб согласно условию
[w]=400/200=2см.
Таким образом, максимальный прогиб wmax = |wC| = 1,38 см меньше допускаемого, и
условие жесткости выполняется.
13

14.

Пример №2
Выберем начало отсчета координаты х
на левом конце балки в точке А и
запишем выражение для изгибающего
момента на всех участках с учетом
правил Клебша :
Подставим это выражение в
дифференциальное уравнение
изогнутой оси (4.16) и проинтегрируем
его дважды:
14

15.

Угол поворота сечения А определим, подставив в выражение для w′(x) на
первом участке значение х = 0, то есть
Чтобы найти прогиб в точке D, в выражение для прогибов w(x) подставляем x = 6 м,
используя все слагаемые этого выражения, так как точка находится на последнем
третьем участке:
Разделим полученные результаты на жесткость балки, чтобы сосчитать угол
поворота в радианах, а прогиб в сантиметрах. Жесткость стальной двутавровой
балки №24:
EI =2⋅104 ⋅3460=6,92⋅107кН·см2.
15

16.

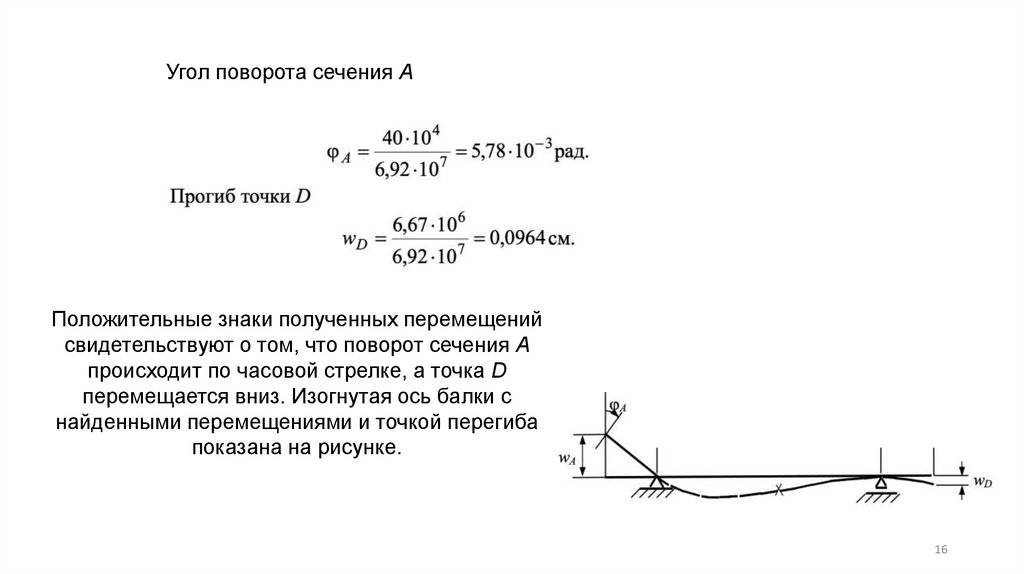
Угол поворота сечения А
Положительные знаки полученных перемещений
свидетельствуют о том, что поворот сечения А
происходит по часовой стрелке, а точка D
перемещается вниз. Изогнутая ось балки с
найденными перемещениями и точкой перегиба
показана на рисунке.
16

17.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра Строительной механики
Авторы:
к.т.н., Войтко Александр Михайлович
[email protected]
17