Похожие презентации:
Расчеты на жесткость при прямом плоском изгибе. Перемещения при изгибе
1.
РАСЧЕТЫ НА ЖЕСТКОСТЬ ПРИПРЯМОМ ПЛОСКОМ ИЗГИБЕ.
Перемещения при изгибе.
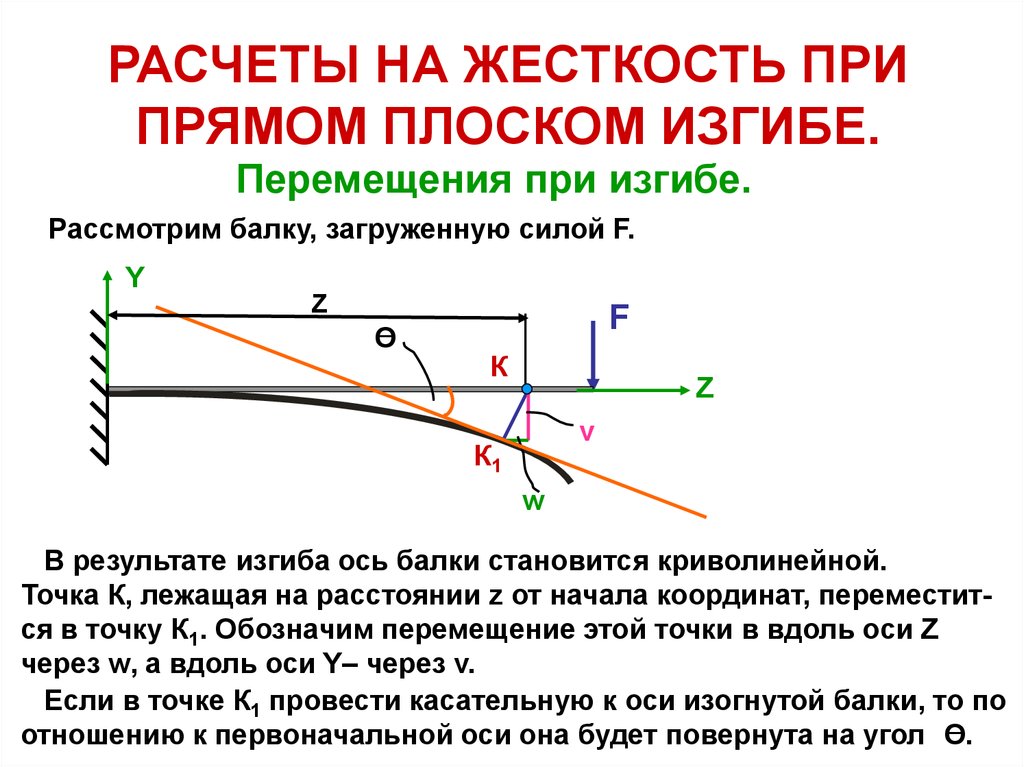
Рассмотрим балку, загруженную силой F.
Y
Z
F
_
O
К
Z
v
К1
w
В результате изгиба ось балки становится криволинейной.
Точка К, лежащая на расстоянии z от начала координат, переместится в точку К1. Обозначим перемещение этой точки в вдоль оси Z
через w, а вдоль оси Y– через v.
Если в точке К1 провести касательную к оси изогнутой балки, то по
_
отношению к первоначальной оси она будет повернута на угол O.
2.
Yℓ
F
_
O
К
К1
v(z)
Z
v
К1
w
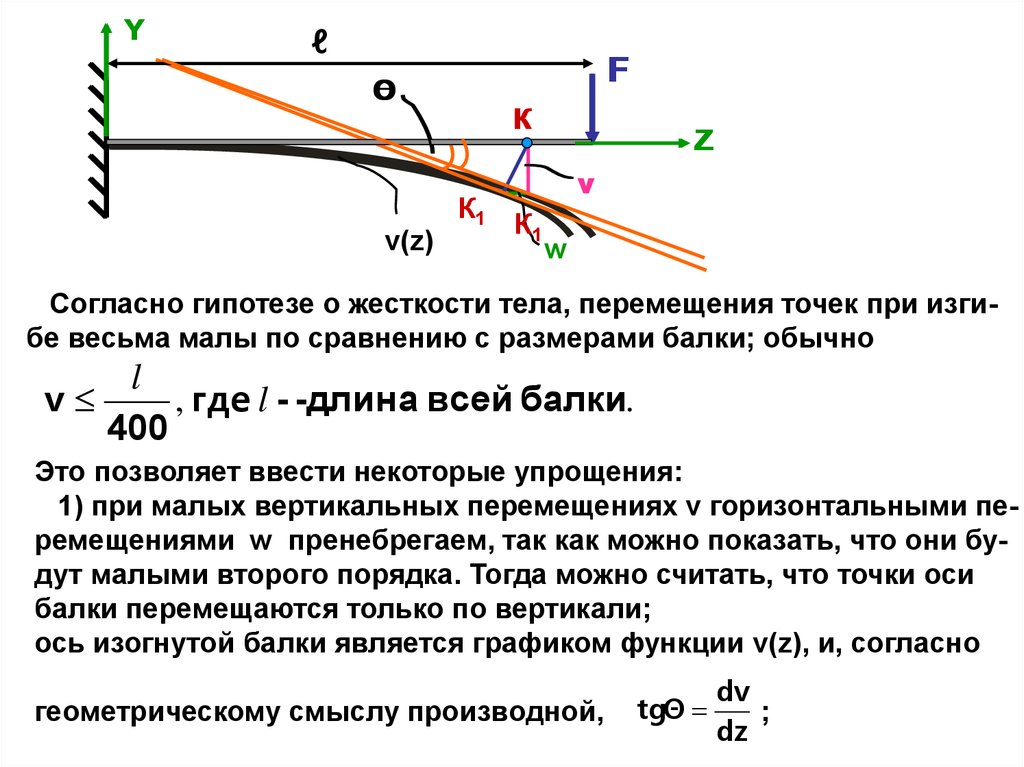
Согласно гипотезе о жесткости тела, перемещения точек при изгибе весьма малы по сравнению с размерами балки; обычно
l
v
, где l - -длина всей балки.
400
Это позволяет ввести некоторые упрощения:
1) при малых вертикальных перемещениях v горизонтальными перемещениями w пренебрегаем, так как можно показать, что они будут малыми второго порядка. Тогда можно считать, что точки оси
балки перемещаются только по вертикали;
ось изогнутой балки является графиком функции v(z), и, согласно
геометрическому смыслу производной,
tgΘ
dv
;
dz
3.
YF
_
O
К
К1
Z
v
v(z)
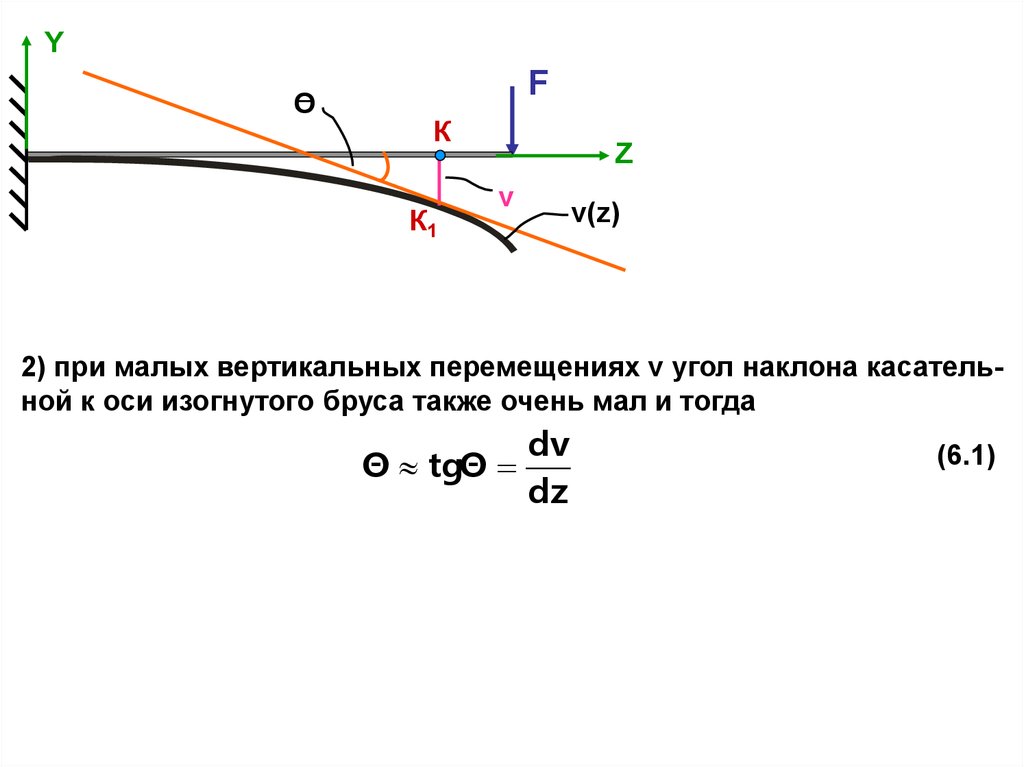
2) при малых вертикальных перемещениях v угол наклона касательной к оси изогнутого бруса также очень мал и тогда
Θ tgΘ
dv
dz
(6.1)
4.
_O
К _
O
К1
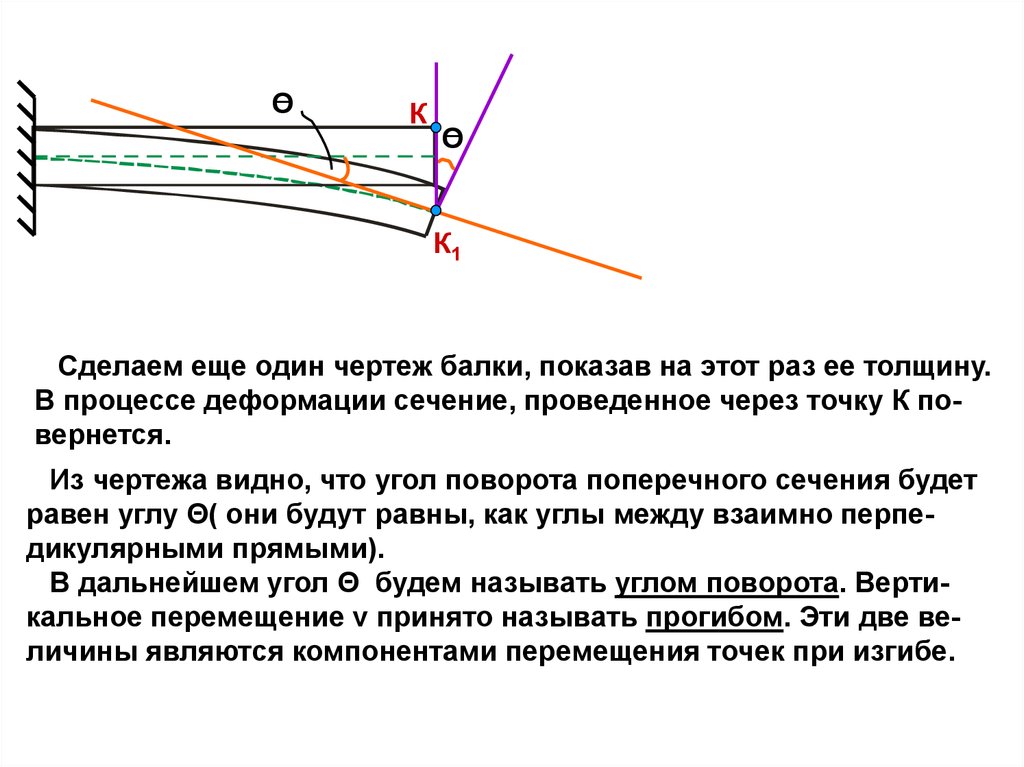
Сделаем еще один чертеж балки, показав на этот раз ее толщину.
В процессе деформации сечение, проведенное через точку К повернется.
Из чертежа видно, что угол поворота поперечного сечения будет
равен углу Θ( они будут равны, как углы между взаимно перпедикулярными прямыми).
В дальнейшем угол Θ будем называть углом поворота. Вертикальное перемещение v принято называть прогибом. Эти две величины являются компонентами перемещения точек при изгибе.
5.
Дифференциальное уравнение оси изогнутогобруса.
При выводе формулы для нормальных напряжений при чистом
изгибе была получена связь между кривизной и изгибающим моментом:
1 Mx
ρ EJx
(6.2)
Из этой формулы следует, что кривизна балки изменяется по тому
же закону, что и величина Mx/EJx. Так, если сечение балки постоянно, балка выполнена из одного и того же материала, то при чистом
изгибе
1 Mx
const.
ρ EJx
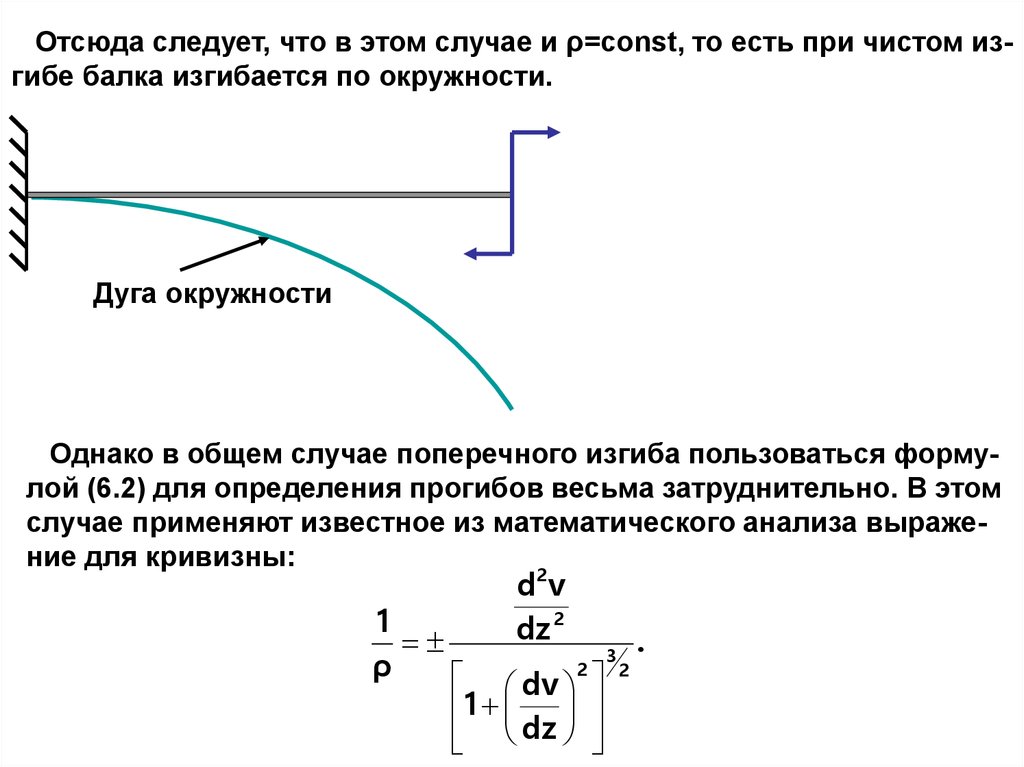
6.
Отсюда следует, что в этом случае и ρ=const, то есть при чистом изгибе балка изгибается по окружности.Дуга окружности
Однако в общем случае поперечного изгиба пользоваться формулой (6.2) для определения прогибов весьма затруднительно. В этом
случае применяют известное из математического анализа выражение для кривизны:
d2 v
dz 2
1
.
3
ρ
dv 2 2
1
dz
7.
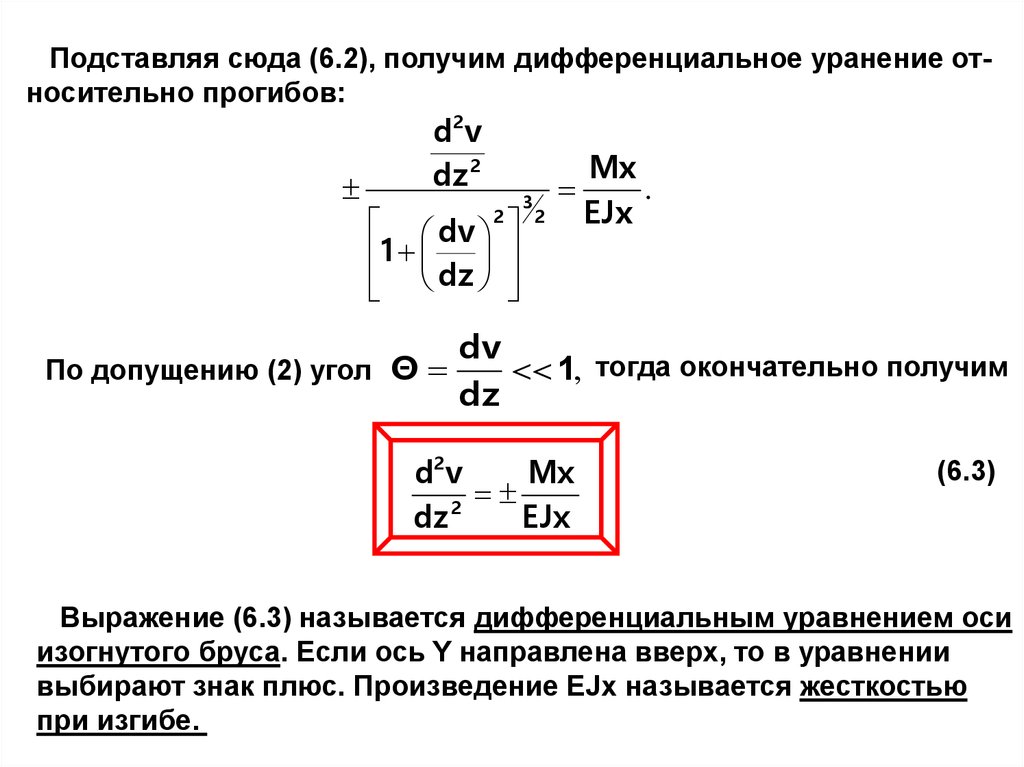
Подставляя сюда (6.2), получим дифференциальное уранение относительно прогибов:d2 v
dz 2
dv
1
dz
По допущению (2) угол Θ
2
3
2
Mx
.
EJx
dv
1, тогда окончательно получим
dz
d2 v
Mx
dz 2
EJx
(6.3)
Выражение (6.3) называется дифференциальным уравнением оси
изогнутого бруса. Если ось Y направлена вверх, то в уравнении
выбирают знак плюс. Произведение EJx называется жесткостью
при изгибе.
8.
Рассмотрим различные методы определения перемещений при изгибе.Метод непосредственного интегрирования.
Этот метод основан на интегрировании уравнения (6.3). Проинтегрировав это уравнение один раз, получим выражение для угла поворота:
dv
Mx
Θ
dz C.
dz
EJx
(6.4)
Проинтегрировав (6.4), получим выражение для прогибов:
v
dv
Mx
dz (
dz C) dz D.
dz
EJx
(6.5)
Если результат вычислений оказывается положительным, то прогиб направлен вверх, то есть совпадает с положительным направлением оси Y.
9.
Для вычисления интегралов, входящих в эти формулы, необходимо сначала записать аналитические выражения для изгибающегомомента Mx и жесткости EJx. Постоянные C и D находятся из граничных условий, то есть из условий закрепления балки.
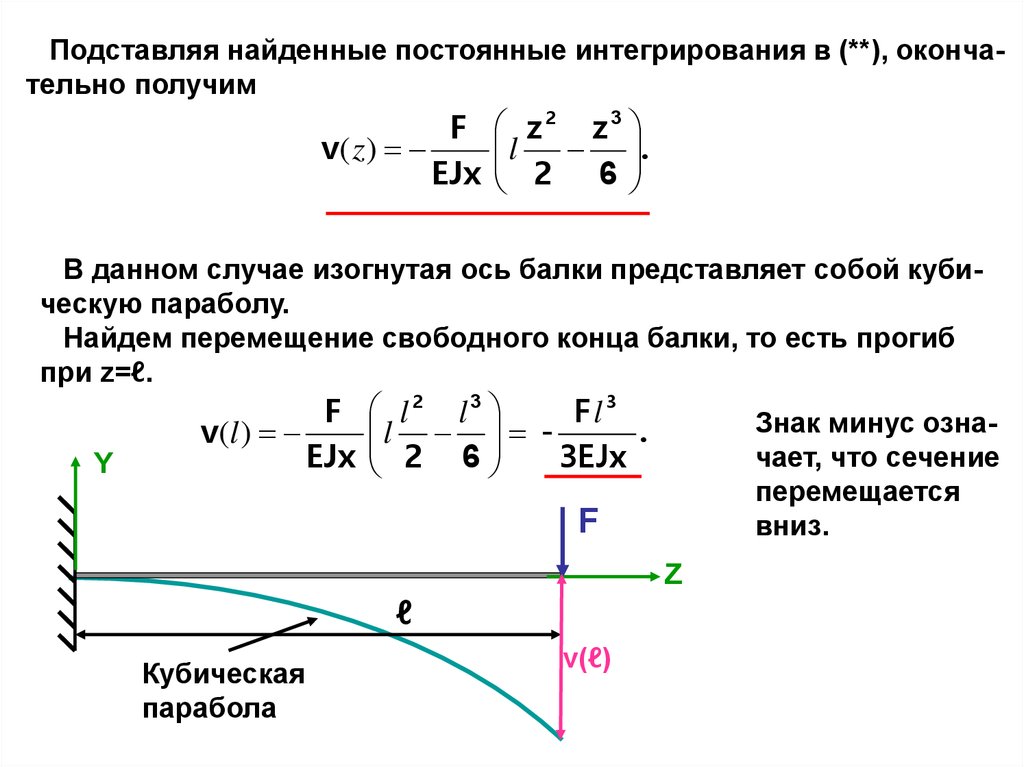
Пример 1.
Определить прогиб свободного конца балки, изображенной на
рисунке, считая жесткость балки постоянной, EJx=Const.
Y
F
Z
ℓ
10.
YF
Z
ℓ
Z
F
Mx
ℓ-Z
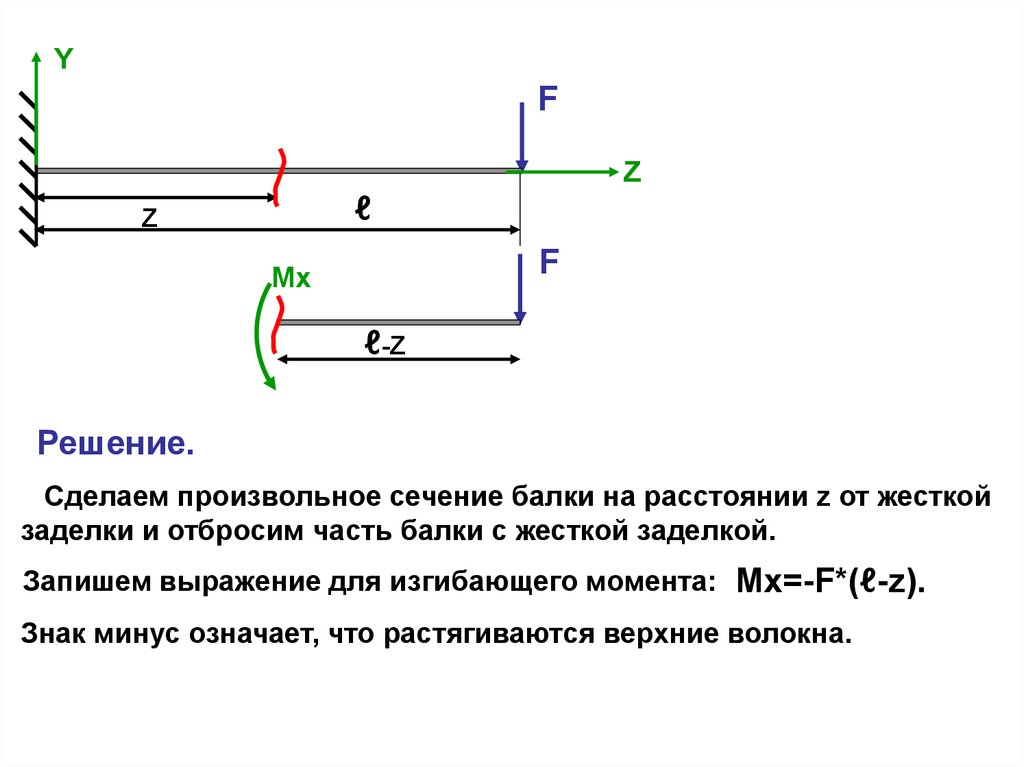
Решение.
Сделаем произвольное сечение балки на расстоянии z от жесткой
заделки и отбросим часть балки с жесткой заделкой.
Запишем выражение для изгибающего момента: Mx=-F*(ℓ-z).
Знак минус означает, что растягиваются верхние волокна.
11.
Подставим полученное выражение в (6.4):dv
Mx
- F ( l - z)
Θ
dz C
dz C
dz
EJx
EJx
F
EJx
F
l z dz C EJx
z2
l z C.
2
(*)
Для получения прогибов проинтегрируем это выражение еще раз:
z2
2
3
- F ( l z - )
F
z
z
2
l Cz D. (**)
v(z) (
C)dz D
EJx
EJx 2 6
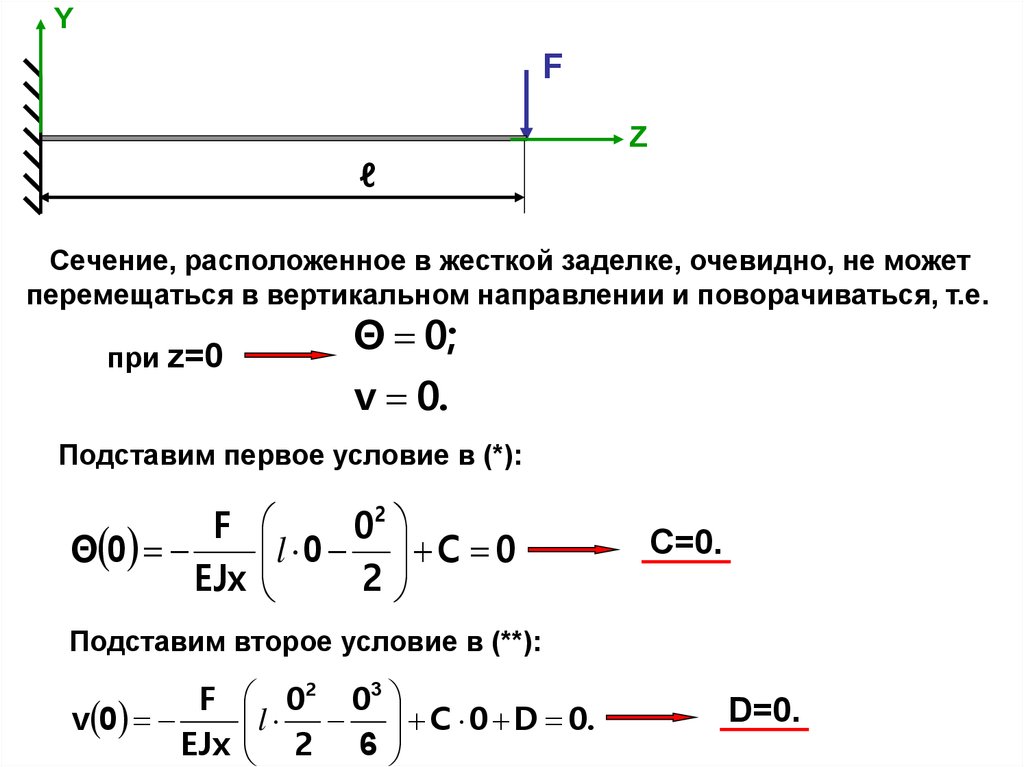
Найдем постоянные интегрирования из граничных условий.
12.
YF
Z
ℓ
Сечение, расположенное в жесткой заделке, очевидно, не может
перемещаться в вертикальном направлении и поворачиваться, т.е.
Θ 0;
при z=0
v 0.
Подставим первое условие в (*):
F
Θ 0
EJx
02
l 0 C 0
2
С=0.
Подставим второе условие в (**):
F
v 0
EJx
02 03
l C 0 D 0.
2 6
D=0.
13.
Подставляя найденные постоянные интегрирования в (**), окончательно получимF
v( z)
EJx
z2 z3
l
.
2 6
В данном случае изогнутая ось балки представляет собой кубическую параболу.
Найдем перемещение свободного конца балки, то есть прогиб
при z=ℓ.
Y
F
v(l )
EJx
l2 l3
Fl3
l .
3EJx
2 6
Знак минус означает, что сечение
перемещается
вниз.
F
Z
ℓ
Кубическая
парабола
v(ℓ)
14.
К достоинствам метода непосредственного интегрирования относится возможность получить функцию прогибов балки, что позволяет при необходимости, построив график этой функции, изобразитьизогнутую ось балки. Недостатком же этого метода является трудоемкость вычислений при увеличении количества участков загружения балки. Так, если балка имеет, например, три участка загружения,
то при интегрировании образуется шесть постоянных интегрирования, для определения которых надо решать систему шести уравнений. Именно вследствие этого недостатка метод непосредственного
интегрирования редко применяется в инженерной практике.
Метод начальных параметров.
Этот метод был разработан группой советских ученых на основе
метода непосредственного интегрирования, но, в отличие от него,
здесь, независимо от количества участков загружения, необходимо
будет определять только две постоянных интегрирования – прогиб
и угол поворота в начале координат. Перемещения в этом методе
находятся с помощью двух формул (даны без вывода).
15.
Для определения прогибов:EJx v z EJx v0 EJx Θ0 z
i
2
z ai
M
i
2
F
i
i
z bi 3
6
4
z ci
q
;
i
i
24
(6.6)
для определения углов поворота:
EJx Θ z EJx Θ0
M z a F
i
i
i
i
i
z bi 2
2
i
3
z ci
q
.
i
6
(6.7)
16.
В этих формулах:Mi,Fi,qi – сосредоточенные моменты, сосредоточенные силы и ин-
тенсивности распределенных нагрузок соответственно,
приложенные к балке, включая и опорные реакции. На
рисунке показаны положительные направления нагрузок;
ai,bi,ci – абсциссы точек приложения сосредоточенных момен-
тов, сосредоточенных сил и начала действия распределенных нагрузок соответственно, отсчитываемые от
начала координат;
Y
Mi
Fi
qi
Z
ai
bi
ci
17.
YMi
О
Fi
qi
Z
Z
ai
bi
ci
z– координата сечения, в котором определяется перемещение.
v0,Θ0– прогиб и угол поворота в начале координат, называемые
начальными параметрами.
При использовании этих формул необходимо соблюдать следующие правила:
1). Начало координат всегда выбирается на левом конце балки;
18.
2). В формулах учитываются только те нагрузки, которые расположены слева от рассматриваемого сечения;3). В случае, если действие распределенной нагрузки заканчивается раньше рассматриваемого сечения, ее продлевают до этого
сечения, а для восстановления действительных грузовых условий
вводят «компенсирующую» нагрузку обратного направления. Дополнительную и компенсирующую нагрузку на расчетной схеме
обычно показывают пунктиром;
Y
qi
Дополнительная
нагрузка
Z
qi
Компенсирующая
нагрузка
4). Если результат вычислений оказывается положительным, то
прогиб направлен вверх, то есть совпадает с положительным направлением оси Y.
19.
Решение задачи методом начальных параметров начинается сопределения самих начальных параметров. При этом могут встретиться следующие случаи:
1). Левый конец балки жестко защемлен. Тогда заданы оба начальных параметра:
v0=0;
Θ0=0.
2). Левый конец балки шарнирно оперт. Тогда задан один начальный параметр:
v0=0;
Θ0 находим из условия
v(а)=0.
а
3). Левый конец балки свободен. Тогда неизвестны оба начальных параметра:
а
с
v0,Θ0 находим из условий
v(a)=0;
v(c)=0.
20.
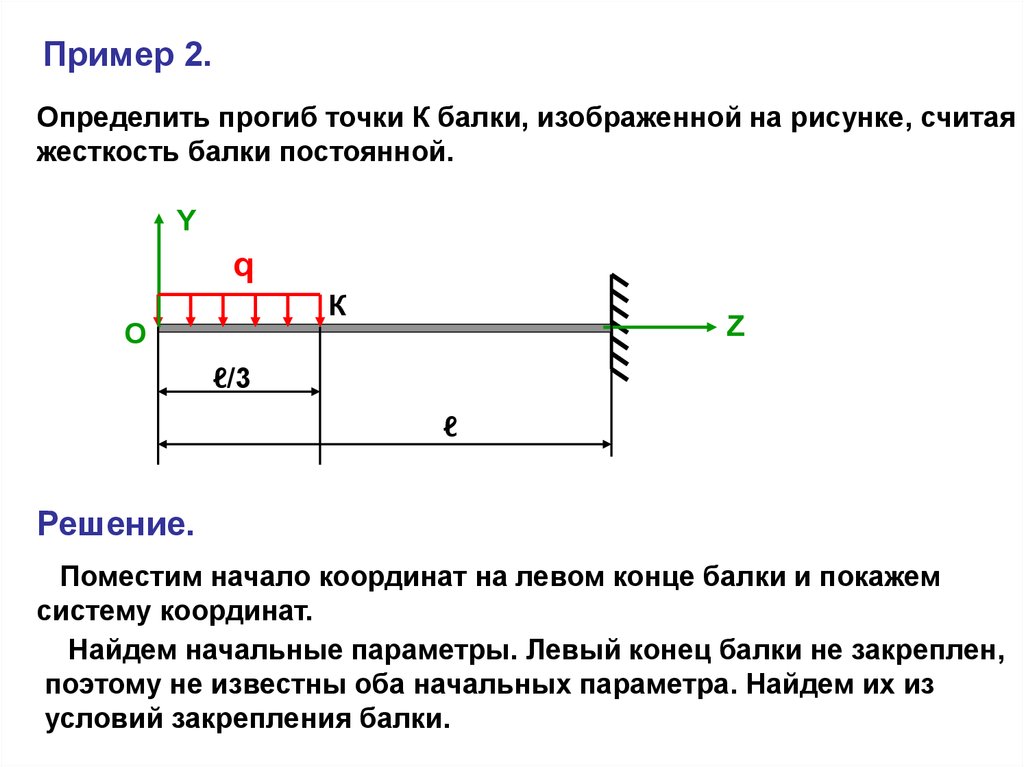
Пример 2.Определить прогиб точки К балки, изображенной на рисунке, считая
жесткость балки постоянной.
Y
q
К
О
Z
ℓ/3
ℓ
Решение.
Поместим начало координат на левом конце балки и покажем
систему координат.
Найдем начальные параметры. Левый конец балки не закреплен,
поэтому не известны оба начальных параметра. Найдем их из
условий закрепления балки.
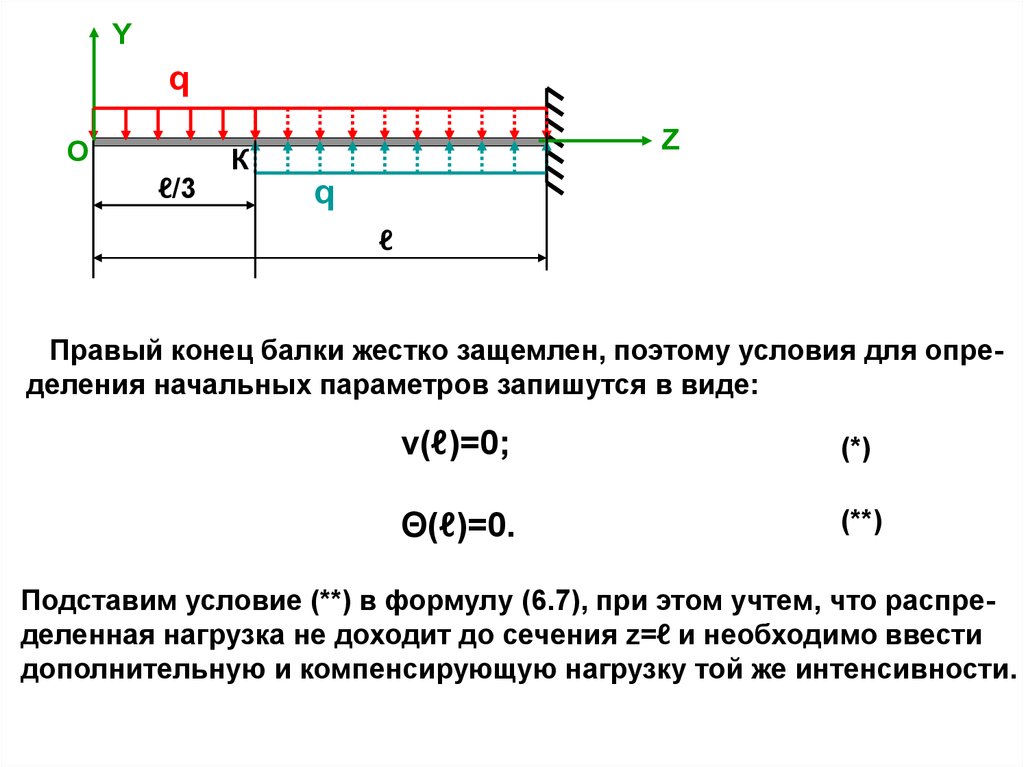
21.
Yq
О
ℓ/3
Z
К
q
ℓ
Правый конец балки жестко защемлен, поэтому условия для определения начальных параметров запишутся в виде:
v(ℓ)=0;
(*)
Θ(ℓ)=0.
(**)
Подставим условие (**) в формулу (6.7), при этом учтем, что распределенная нагрузка не доходит до сечения z=ℓ и необходимо ввести
дополнительную и компенсирующую нагрузку той же интенсивности.
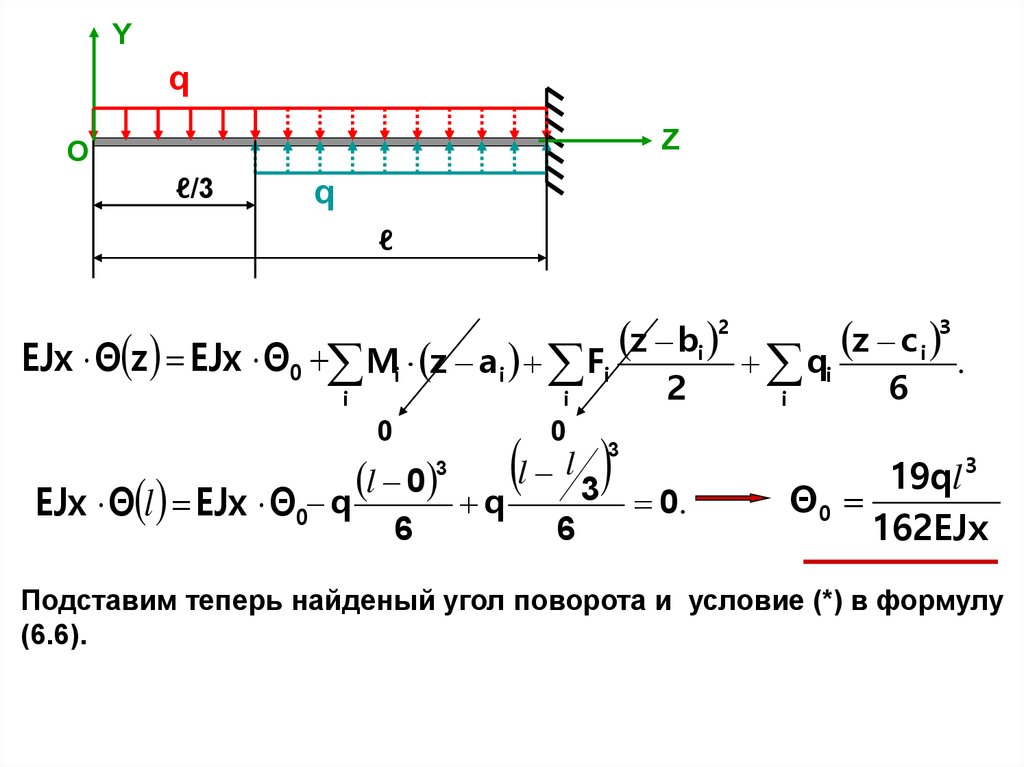
22.
Yq
Z
О
ℓ/3
q
ℓ
EJx Θ z EJx Θ0 Mi z a i Fi
i
i
0
l 0
q
EJx Θ l EJx Θ0
z bi 2
3
6
q
0
l l
6
3
2
3
0.
i
3
z ci
q
.
i
6
19ql 3
Θ0
162EJx
Подставим теперь найденый угол поворота и условие (*) в формулу
(6.6).
23.
Yq
Z
О
ℓ/3
q
ℓ
EJx v z EJx v0 EJx Θ0 z
Mi
i
0
z a i
2
2
Fi
z bi
i
0
3
6
qi
z c i
4
24
i
4
;
4
l l
l 0
19q l 3
3 0.
q
EJx v l EJx v 0 EJx
l q
24
24
162EJx
163ql 4
v0
1944EJx
24.
Начальные параметры найдены. Теперь найдем прогиб точки К,подставляя найденные значения в формулу (6.6).
Y
q
К
О
Z
ℓ/3
ℓ
EJx v z EJx v0 EJx Θ0 z
i
2
z ai
M
i
0
2
F
i
i
z bi 3
6
i
0
4
z ci
q
;
i
24
4
l 0
163
q
l
19q
l
EJx v z l EJx
EJx
l q 3
.
3
3
1944EJx
162EJx
24
4
3
25.
qК
vK
11ql 4
ql 4
vK
0,045
243EJx
EJx
Величина vK получилась отрицательной, что означает, что точка К
перемещается вниз.
26.
Энергетические методы определенияперемещений.
Эти методы основаны на использовании формулы потенциальной энергии деформаций. По аналогии с осевым растяжением-сжатием запишем формулу для определения потенциальной энергии
при изгибе:
Mx
Qy i2
U
dz
dz
2G i Ai
i 0 2E iJx i
i
0
li
2
i
li
Как показывают расчеты, при изгибе балок вклад поперечной силы в величину U пренебрежимо мал по сравнению с вкладом изгибающего момента, поэтому в дальнейшем будем определять потенциальную энергию по упрощенной формуле:
Mx i2
U
dz
i 0 2E iJx i
li
(6.8)
27.
Рассмотрим два энергетических метода определения перемещений.Теорема Кастильяно.
F1
1
F2
2
V1
V2
рис.1
Для вывода теоремы
Кастильяно рассмотрим
упругую систему в виде
однопролетной балки,
загруженной двумя независимыми силами F1
и F2.
Под действием этих сил балка прогибается , при этом сечение 1
прогибается на величину V1, а сечение 2 – на величину V2 (рис.1).
Потенциальная энергия деформации этой балки определяется
окончательными значениями внешних сил и не зависит от порядка
их приложения. Найти эту энергию можно путем сложения работ
сил при любой последовательности их приложения (на основании
гипотезы о независимости действия сил).
28.
F2F1
1
2
V1
V2
рис.1
F1
F2
V11
2
V21
1
рис.2
F2
F1
1
2
V22
V12
рис.3
Приложим сначала статически силу F1, а затем
силу F2. При нагружении
силой F1 сечения 1 и 2
перемещаются на величины V11 и V21 соответственно (рис.2).
Работу силы F1 на перемещении V11 найдем
по формуле (2.22):
F V
A11 1 11 .
2
Приложим теперь к уже
изогнутой балке силу
F2. Сечения 1 и 2 получат дополнительные
перемещения V12 и V22
соответственно (рис.3).
Из рисунков следует,
что V1=V11+V12 и
V2=V21+V22.
29.
Работа силы F2 на перемещении V22 равна, согласно формуле(2.22),
F V
A 22 2 22 .
2
Сила F1 в процессе нагружения балки силой F2 остается неизменной, поэтому ее работу вычисляем по обычной формуле теоретической механики:
A12 F1 V12 .
Потенциальная энергия деформаций будет равна сумме этих
работ:
U A11 A12 A 22
1
1
F1 V11 F1 V12 F2 V22 .
2
2
В теме «Осевое растяжение-сжатие» было показано, что в зоне
упругих деформаций, перемещения прямо пропорционально вызывающей их силе:
30.
V11=k*F1.(*)
С учетом этого выражение для потенциальной энергии деформаций перепишется в виде:
1
1
U F1 k F1 F1 V12 F2 V22 .
2
2
Продифференцируем это выражение по силе F1. При этом учтем,
что перемещения V12, V22 не зависят от этой силы.
U
k F1 V12 .
F1
С учетом (*) получим
U
k F1 V12 V11 V12 V1.
F1
31.
Аналогично можно показать, что если нагружение балки начатьс силы F2, то получим
U
V2 .
F2
Если нагрузить балку вместо сосредоточенной силы сосредоточенным моментом, то, продифференцировав выражение для потенциальной энергии по этому моменту, получим величину угла поворота. Таким образом, можно сформулировать теорему Кастильяно следующим образом:
« Частная производная от потенциальной энергии деформаций по
сосредоточенной нагрузке равна перемещению сечения, в котором
эта нагрузка приложена».
Если результат вычислений положителен, то направление перемещения совпадает с направлением соответствующей нагрузки.
32.
Пример 3.Y
F
Z
Z
ℓ
Используя теорему Кастильно, определить
прогиб свободного конца балки, изображенной
на рисунке. Жесткость
балки считать постоянной.
Решение.
Составим выражение для потенциальной энергии деформаций.
Для этого сначала найдем изгибающий момент в произвольном сечении балки с координатой z.
Это уже было сделано в примере 1:
Mx=-F*(ℓ-z).
Подставим изгибающий момент в (6.8).
33.
Mxi2F l z
U
dz
dz
2EJx
i 0 2E iJx i
0
li
F
2EJx
2
2
l
F
l
F l
l 2lz z dz
2EJx 3
6EJx
l
0
2
2
2
3
2
3
Продифференцируем это выражение по силе F и найдем прогиб:
U 2F l 3
F l3
v
F
6EJx
3EJx
Знак плюс указывает на то, что направление перемещения совпадает с направлением действующей силы, то есть прогиб направлен вниз ( сравни с результатом примера 1).
34.
Теорема Максвелла-Мора.Теорема Кастильяно не позволяет определить перемещение того
сечения, к которому не приложена нагрузка. Однако из этого затруднения есть простой выход. Чтобы определить прогиб или угол поворота в точке, где по условию задачи сила отсутствует, в этой точке
следует приложить соответствующую фиктивную нагрузку. Далее,
написав выражение для потенциальной энергии от системы сил,
включая фиктивную нагрузку, следует взять производную от этого
выражения по фиктивной нагрузке и в полученном выражении для
перемещения положить фиктивную нагрузку равной нулю.
Рассмотрим этот процесс применительно к изгибу балки.
35.
Предположим, что требуется определить перемещение некоторойточки К балки, в которой не приложены никакие нагрузки.
Приложим в точке К фиктивную силу Ф.
Ф
q
К
F
Z
Запишем выражение для изгибающего момента в произвольном
сечении балки. На основании принципа независимости действия
сил
F
Ф
MX z MX z MX z , где
MFX
-- изгибающий момент от заданных нагрузок;
MФX
-- изгибающий момент от фиктивной нагрузки.
1
Последний, очевидно, можно переписать в виде: MФ
Ф
M
X
X,
1
где MX -- изгибающий момент от фиктивной нагрузки, равной
единице, Ф=1, который называется единичным моментом.
36.
Составим выражение для потенциальной энергии деформаций:li
Mx
U
dz
i 0 2E iJx i
2
i
li
i
0
M
F
Xi
Ф M
2E iJx i
1 2
Xi
dz;
Продифференцируем это выражение по силе Ф и найдем перемещение:
U
Ф
i 0
li
2 MFX i Ф M1Xi M1X
2E iJx i
dz;
Теперь «вспомним», что на самом деле нагрузки Ф нет, и в полученное выражение подставим Ф=0.
MFX M1X
dz
E iJx i
i 0
li
(6.9)
37.
Формула (6.9) выражает содержание теоремы Максвелла-Мора.По этой формуле можно определять и прогиб, и угол поворота.
При определении прогиба в качестве фиктивной нагрузки берут
безразмерную сосредоточенную силу, равную единице, а при определении угла поворота фиктивной нагрузкой является безразмерный сосредоточенный момент, также равный единице.
Знак плюс результата указывает на то, что направление перемещения совпадает с направлением единичной фиктивной нагрузки.
Метод Мора по сравнению с другими рассмотренными методами
обладает одним очень важным преимуществом – он является универсальным в смысле выбора вида деформации и объекта применения, то есть его можно использовать при определении перемещений не только при изгибе, но и при растяжении, сжатии, кручении;
и не только балок,но и рам, арок, ферм, пространственных брусьев и т.д.
38.
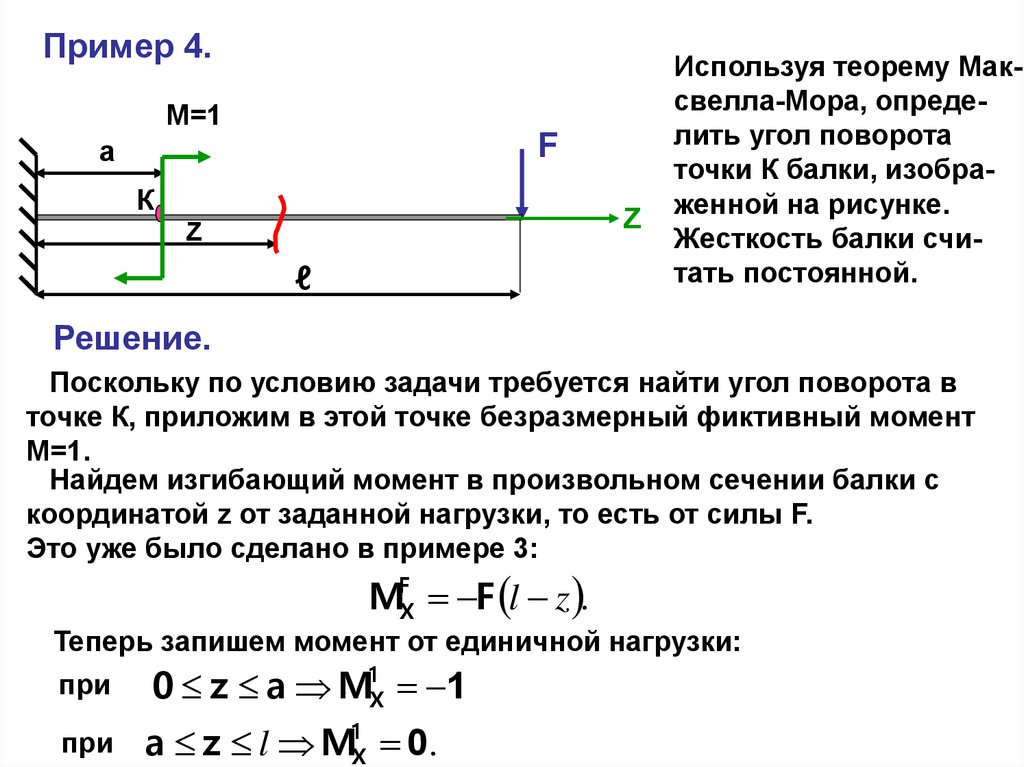
Пример 4.М=1
F
а
К
Z
Z
ℓ
Используя теорему Максвелла-Мора, определить угол поворота
точки К балки, изображенной на рисунке.
Жесткость балки считать постоянной.
Решение.
Поскольку по условию задачи требуется найти угол поворота в
точке К, приложим в этой точке безразмерный фиктивный момент
М=1.
Найдем изгибающий момент в произвольном сечении балки с
координатой z от заданной нагрузки, то есть от силы F.
Это уже было сделано в примере 3:
MFX F l z .
Теперь запишем момент от единичной нагрузки:
при
0 z a M1X 1
при
а z l M1X 0.
39.
Подставим эти выражения в (6.9):MFX M1X
1
Θ
dz
E iJx i
EJx
i 0
li
1
EJx
F
a F l z 0 dz EJx
F
EJx
a2
la
2
l
a
F l z 1 dz
0
a
F
l
z
dz
0
EJx
a
z
lz -
2 0
2
Пусть а=ℓ/3. Тогда
F l2
l2
5F
Θ
EJx 3 32 2 18EJx
Знак плюс результата указывает на то, что направление перемещения совпадает с направлением единичного момента, то есть сечение К поворачивается по часовой стрелке.
40.
Основным недостатком метода Мора является необходимостьсоставления аналитических выражений для изгибающих моментов
MF и M1. Это особенно неудобно при определении перемещений в
брусе, имеющим большое количество участков загружения. Однако,
если брус состоит из участков с постоянной в пределах каждого
участка жесткостью EJx, операцию вычисления интеграла Мора можно значительно упростить, применяя для этого формулы численного
интегрирования – формулу трапеций или формулу Симпсона.
В этом случае для определения перемещений какого-либо сечения
балки необходимо выполнить следующие операции:
1) построить так называемую грузовую эпюру, то есть эпюру изгибающих моментов MF от заданной нагрузки;
2) построить единичную балку, то есть снять с рассматриваемой
балки все нагрузки, и к сечению, перемещение которого надо определить, приложить фиктивную силу, равную единице, если надо определить прогиб, или фиктивный момент, равный единице, если определяется угол поворота;
3) построить так называемую единичную эпюру, то есть эпюру изгибающих моментов M1 от фиктивной нагрузки;
4) разбить обе эпюры на участки перемножения;
41.
5) применить к каждому участку формулу численного интегрирования, используя формулу трапеций, если на грузовая эпюра научастке ограничена прямой линией, или формулу Симпсона, которая применима и для прямолинейных, и для криволинейных участков (см. ниже).
6) сложить полученные результаты.
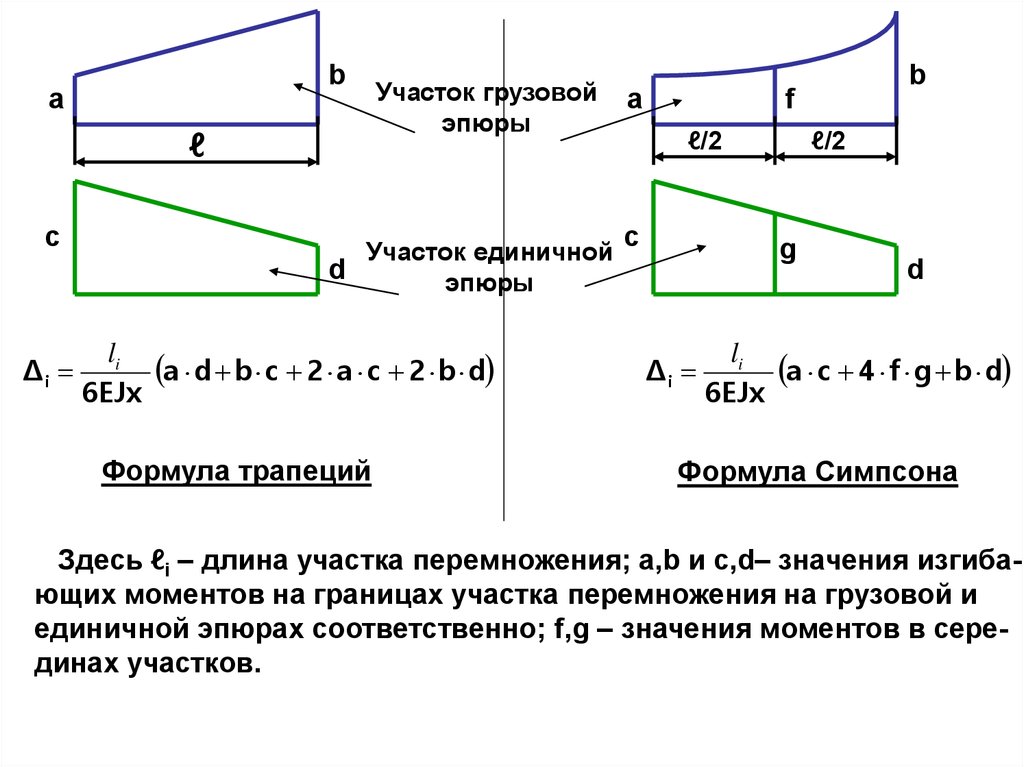
42.
ba
ℓ
c
Δi
Участок грузовой
эпюры
Участок единичной
d
эпюры
li
a d b c 2 a c 2 b d
6EJx
Формула трапеций
a
b
f
ℓ/2
c
ℓ/2
g
Δi
d
li
a c 4 f g b d
6EJx
Формула Симпсона
Здесь ℓi – длина участка перемножения; a,b и c,d– значения изгибающих моментов на границах участка перемножения на грузовой и
единичной эпюрах соответственно; f,g – значения моментов в серединах участков.
43.
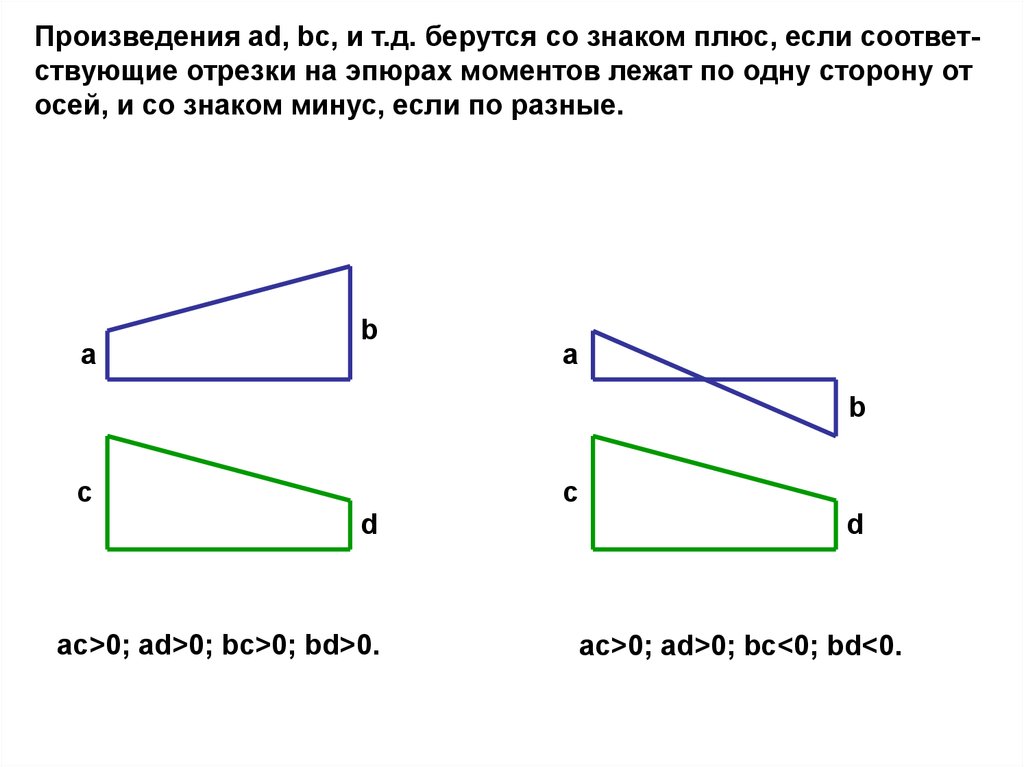
Произведения ad, bc, и т.д. берутся со знаком плюс, если соответствующие отрезки на эпюрах моментов лежат по одну сторону отосей, и со знаком минус, если по разные.
a
b
a
b
c
c
d
ac>0; ad>0; bc>0; bd>0.
d
ac>0; ad>0; bc<0; bd<0.
44.
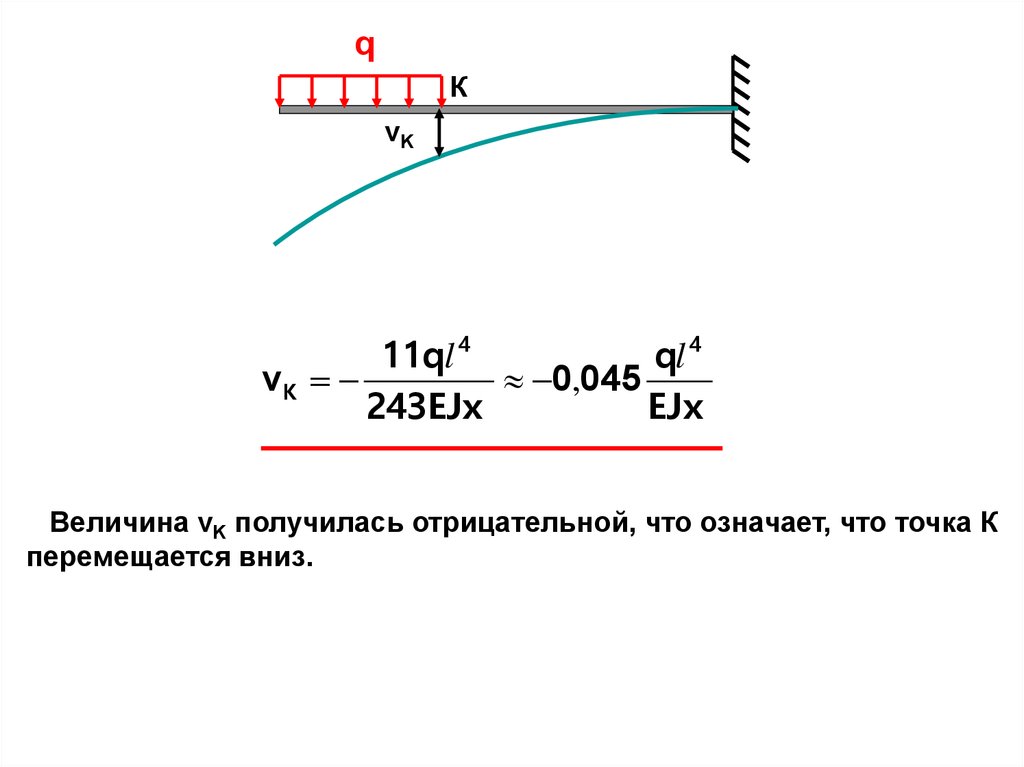
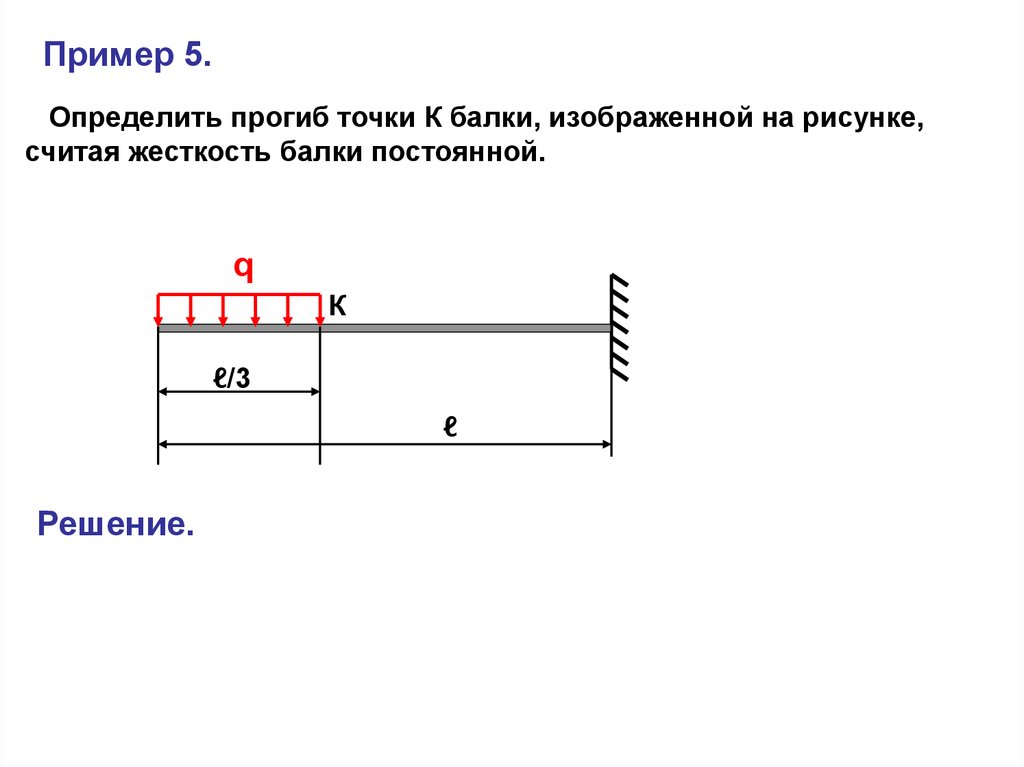
Пример 5.Определить прогиб точки К балки, изображенной на рисунке,
считая жесткость балки постоянной.
q
К
ℓ/3
ℓ
Решение.
45.
qК
2ℓ/3
ℓ/3
qℓ2/18
5qℓ2/18
MFx
F 1
К
ℓ/3
2ℓ/3
2ℓ/3 M1x
1). Построим эпюру изгибающих моментов для данной балки, то есть грузовую эпюру MFx. В дальнейшем эпюры, предназначенные для определения
перемещений, штриховать
не будем.
2). Построим единичную балку. Поскольку по условию задачи требуется определить
прогиб т.К, приложим на единичной балке в т.К безразмерную единичную силу.
3). Построим единичную эпюру, то есть эпюру изгибающих моментов M1x для единичной балки.
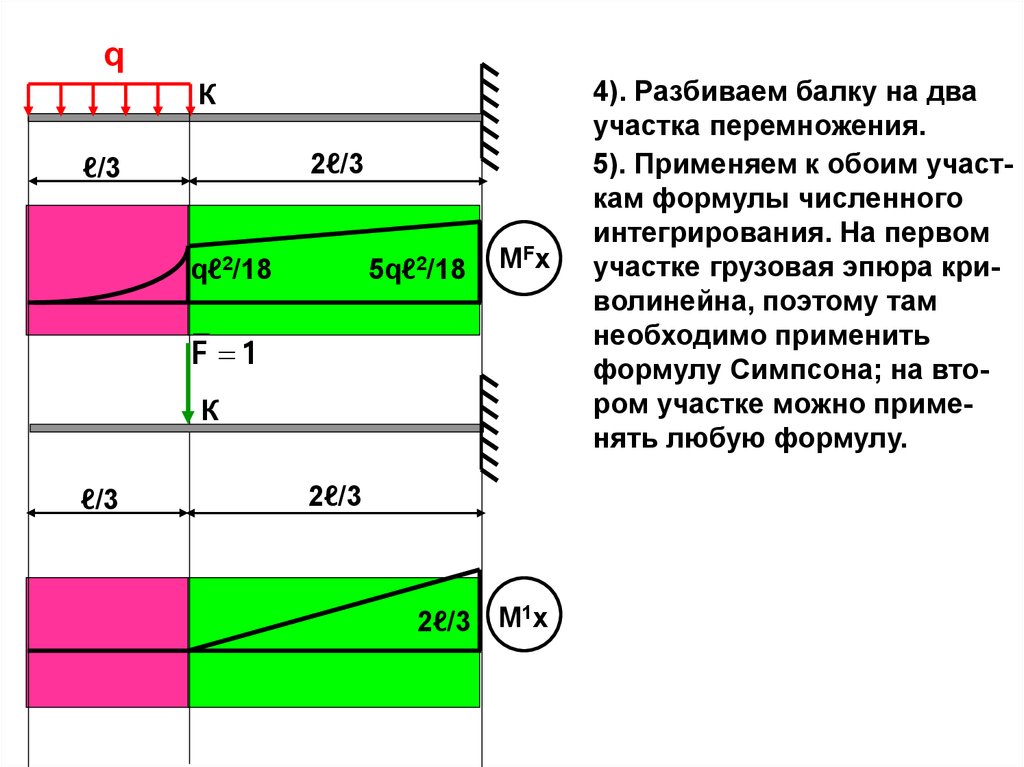
46.
qК
2ℓ/3
ℓ/3
qℓ2/18
5qℓ2/18
MFx
F 1
К
ℓ/3
2ℓ/3
2ℓ/3 M1x
4). Разбиваем балку на два
участка перемножения.
5). Применяем к обоим участкам формулы численного
интегрирования. На первом
участке грузовая эпюра криволинейна, поэтому там
необходимо применить
формулу Симпсона; на втором участке можно применять любую формулу.
47.
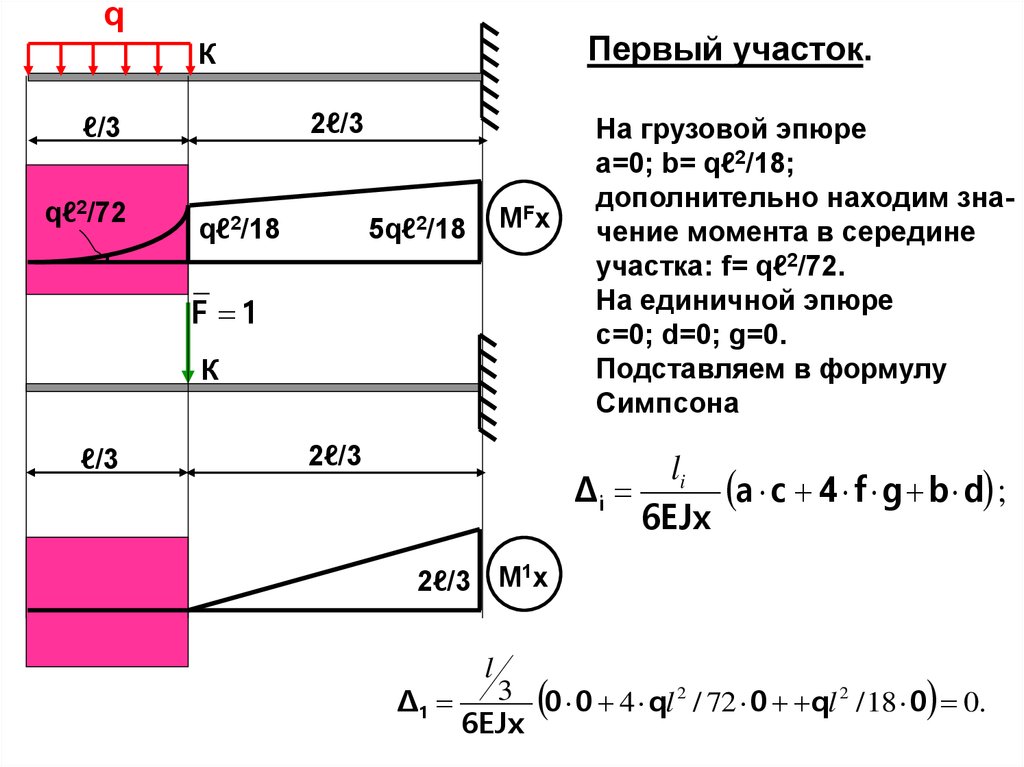
qПервый участок.
К
2ℓ/3
ℓ/3
qℓ2/72
MFx
5qℓ2/18
qℓ2/18
F 1
К
ℓ/3
2ℓ/3
На грузовой эпюре
а=0; b= qℓ2/18;
дополнительно находим значение момента в середине
участка: f= qℓ2/72.
На единичной эпюре
с=0; d=0; g=0.
Подставляем в формулу
Симпсона
li
a c 4 f g b d ;
Δi
6EJx
2ℓ/3 M1x
Δ1
l
3 0 0 4 ql 2 / 72 0 ql 2 / 18 0 0.
6EJx
48.
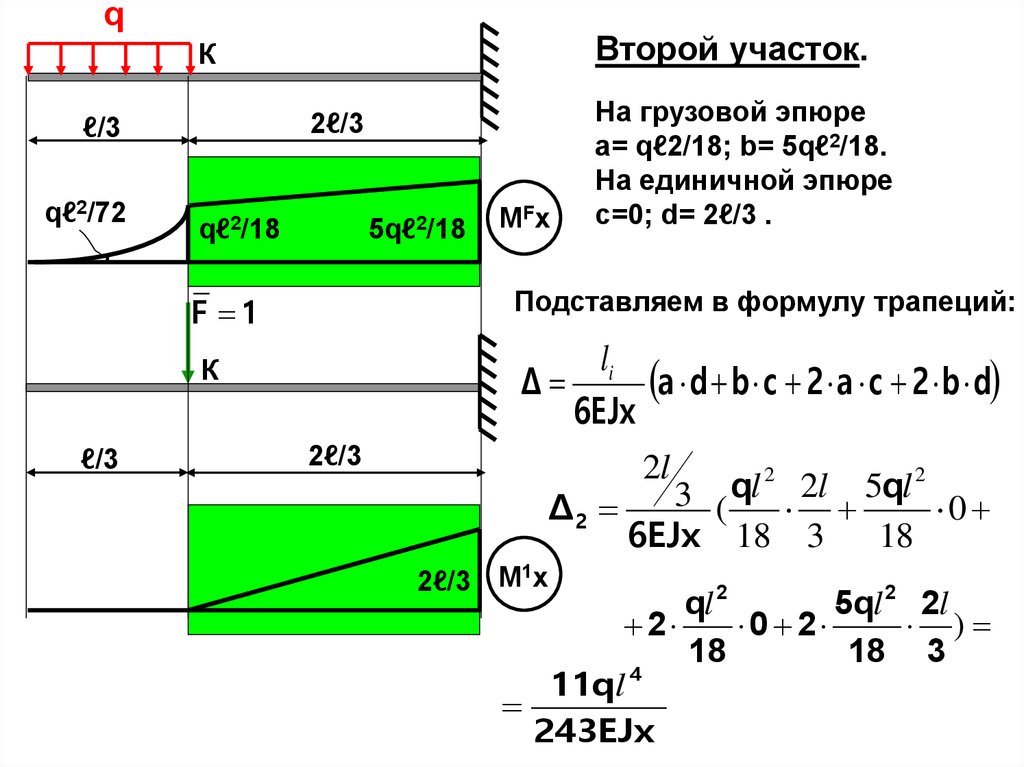
qВторой участок.
К
2ℓ/3
ℓ/3
qℓ2/72
5qℓ2/18
qℓ2/18
Подставляем в формулу трапеций:
F 1
li
a d b c 2 a c 2 b d
Δ
6EJx
К
ℓ/3
MFx
На грузовой эпюре
а= qℓ2/18; b= 5qℓ2/18.
На единичной эпюре
с=0; d= 2ℓ/3 .
2ℓ/3
2l
2
2
q
l
2
l
5
q
l
3 (
Δ2
0
6EJx 18 3
18
2ℓ/3 M1x
ql 2
5ql 2 2l
2
0 2
)
18
18 3
4
11ql
243EJx
49.
Складываем полученные результаты и находим прогиб т.К:vК 1 2 0
11ql 4
243EJx
11ql 4
ql 4
0,045
243EJx
EJx
Знак плюс результата указывает на то, что направление перемещения совпадает с направлением единичной фиктивной нагрузки,
то есть сечение К перемещается вниз (сравни результаты
примера 2).





























 Механика
Механика








