Перемещения при изгибе

1. Перемещения при изгибе

Под расчетом на жесткость понимают оценку упругой податливости балки
под действием приложенных нагрузок и подбор таких размеров
поперечного сечения, при которых перемещения не будут превышать
установленных нормами пределов.
f м акс f
l
400...800
Условие жесткости при изгибе
Перемещение центра тяжести сечения по направлению перпендикулярному к
оси балки, называется прогибом. Прогиб обозначается буквой w
Наибольший прогиб в пролете или на консоли балки, называется стрелой
прогиба и обозначается буквой f.
Угол, , на который каждое сечение поворачивается по отношению к своему
первоначальному положению и есть угол поворота.
Угол поворота считается положительным, при повороте сечения против
хода часовой стрелки
Угол поворота сечения равен значению производной от прогиба по
координате Z в этом же сечении, то есть:
d
dz

2. Уравнение упругой линии балки

d 2
M ( z)
2
EI x
d z
Существуют три метода решения дифференциального уравнения упругой
линии балки. Это метод непосредственного интегрирования, метод Клебша и
метод начальных параметров.
Метод непосредственного интегрирования
Проинтегрировав уравнение упругой линии балки первый раз, получают
выражение для определения углов поворота:
EI x
d
dM ( z )
EI x ( z )
C
dz
dz
Интегрируя второй раз, находят выражения для определения прогибов:
dM ( z ) 2
EI x ( z )
Cz D
2
d z
Значения постоянных интегрирования С и D определяют из начальных
условий на опорах балки

3. Уравнение упругой линии балки

Метод Клебша
Для составления уравнений необходимо выполнить следующие основные
условия:
•начало координат, для всех участков, необходимо расположить в крайнем
левом конце балки;
•интегрирование дифференциального уравнения упругой линии балки
проводить, не раскрывая скобок;
•при включении в уравнение внешнего сосредоточенного момента М его
необходимо помножить на (Z-a)0 где а - координата сечения, в котором
приложен момент;
•в случае обрыва распределенной нагрузки ее продлевают до конца балки, а
для восстановления действительных условий нагружения вводят
«компенсирующую» нагрузку обратного направления

4. Уравнение упругой линии балки

Метод начальных параметров
Для углов поворота:
2
2
3
M pi z d i 1 M i z ai
Ri z d i
Fi z bi
qi z ci
0
2 EI x
EI x
EI x
1
2
6
Для прогибов:
3
2
3
4
M pi z d i
Ri z d i
Fi z bi
qi z ci
1 M i z ai
w w0 0 z
6 EI x
2 EI x
EI x
2
6
24
2
Где —угол поворота сечения, w—прогиб, 0 - угол поворота в начале
координат, w0—прогиб в начале координат, di—расстояние от начало
координат до i-той опоры балки, ai—расстояние от начало координат до точки
приложения сосредоточенного момента Mi , bi—расстояние от начало
координат до точки приложения сосредоточенной силы Fi , сi—расстояние от
начало координат до начала участка распределенной нагрузки qi , Ri и Мрi—
реакция и реактивный момент в опорах балки.

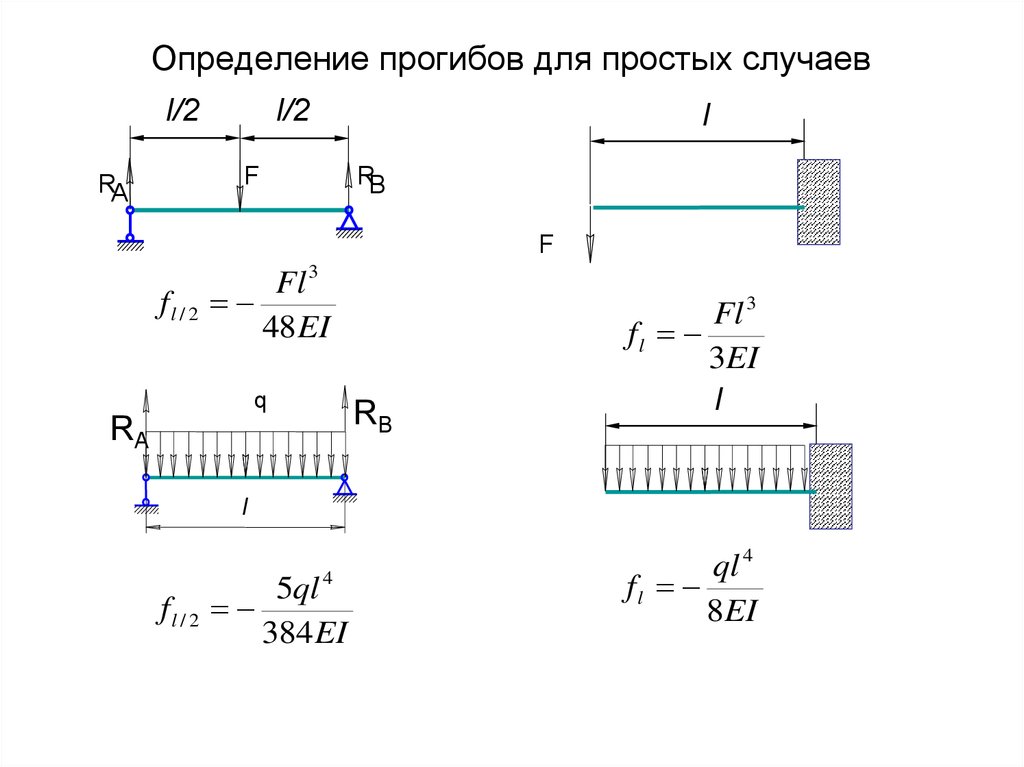
5. Определение прогибов для простых случаев

l/2
l/2
F
RA
l
RB
F
fl / 2
Fl 3
48 EI
q
RA
RВ
Fl 3
fl
3EI
l
l
fl / 2
5ql 4
384 EI
ql 4
fl
8EI