Геометрическая фигура пирамида

1. Пирамида

МБОУ СОШ №5 – «Школа здоровья и развития»
Пирамида
Учитель математики  Семёнова Е.Ю.

2. Содержание

Примеры пирамид 
Определение пирамиды
Виды пирамид
Правильные пирамиды
Построение правильной пирамиды
Свойства правильной пирамиды
Усеченная пирамида
Площадь поверхности пирамиды

3. Пирамиды древности

4. Пирамиды древности

5. Пирамиды древности

6. Магические пирамиды

7. Пирамиды

8. Примеры пирамид

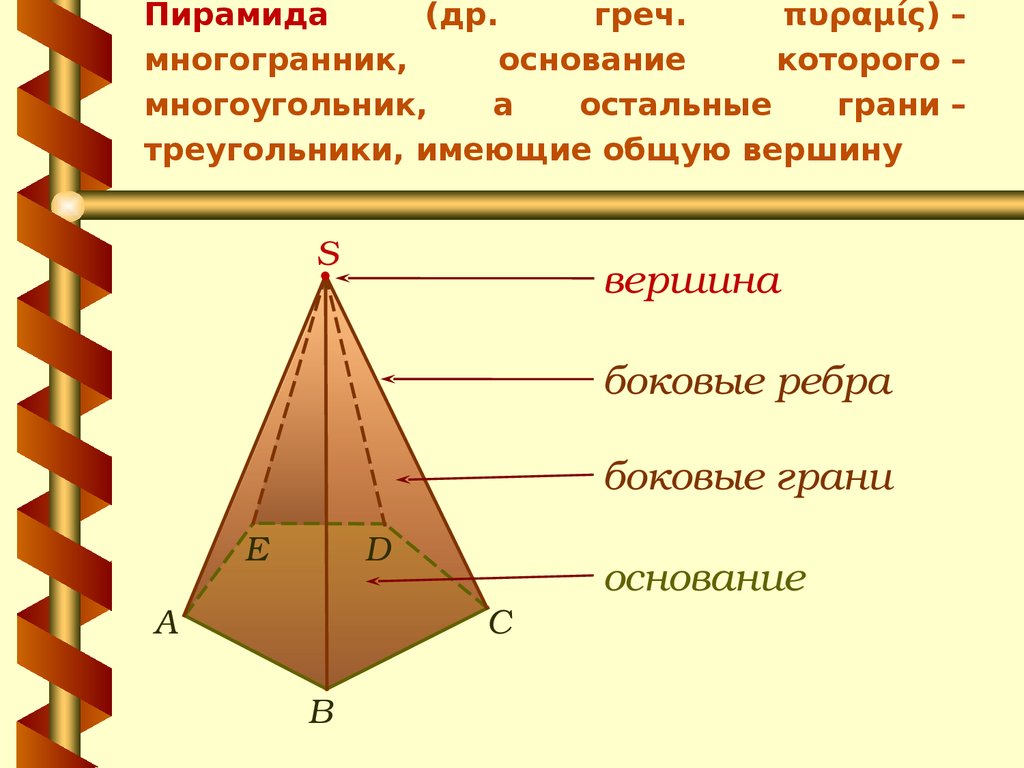
9. Пирамида (др. греч. πυραμίς) – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину

S
вершина
боковые ребра
боковые грани
D
E
А
C
B
основание 

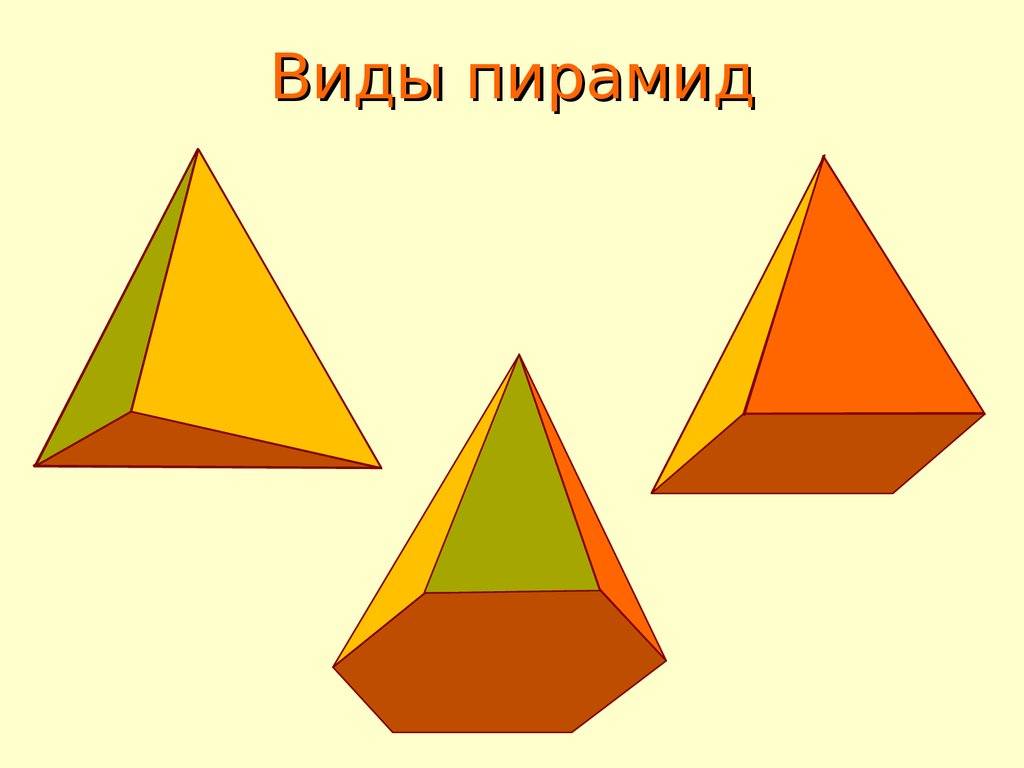
10. Виды пирамид

11. Площадь поверхности пирамиды

Площадь  полной  поверхности  пирамиды  равна 
сумме  площадей  основания  и  боковой 
поверхности.
S
Sполн. 
= Sосн.
 + Sбок.
 
полн. 
осн.
бок.
l 
D
А
С
а 
Н
О
В

12.

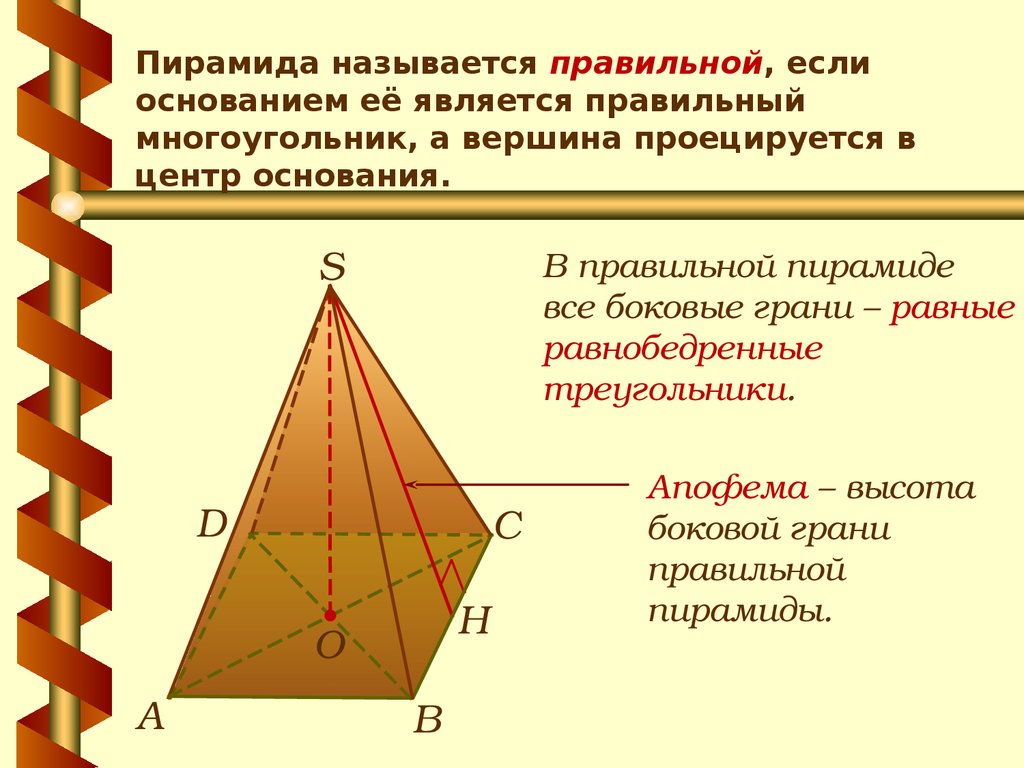
Пирамида называется правильной, если
основанием её является правильный
многоугольник, а вершина проецируется в
центр основания.
S
В правильной пирамиде 
все боковые грани – равные 
равнобедренные 
треугольники. 
D
С
Н
О
А
В
Апофема – высота 
боковой грани 
правильной 
пирамиды.

13. Теорема о площади боковой поверхности правильной пирамиды

Площадь  боковой  поверхности  правильной 
пирамиды  равна  половине  произведения 
периметра основания на апофему
S
Sбок.
 = ½ Pосн.
   SH 
бок.
осн.
d 
D
Док – во:
Sбок = (½ad + ½ad + ½ad + … ) = 
= ½ d (a + a + a + …)= ½Pосн.d
Pосн. 
А
С
а 
Н
О
В

14. Объем пирамиды

Объем  пирамиды  равен  1/3  произведения 
площади основания на высоту.
S
Vпир.
 = 1/3 Sосн
   h 
пир.
осн
h 
D
А
С
а 
О
В

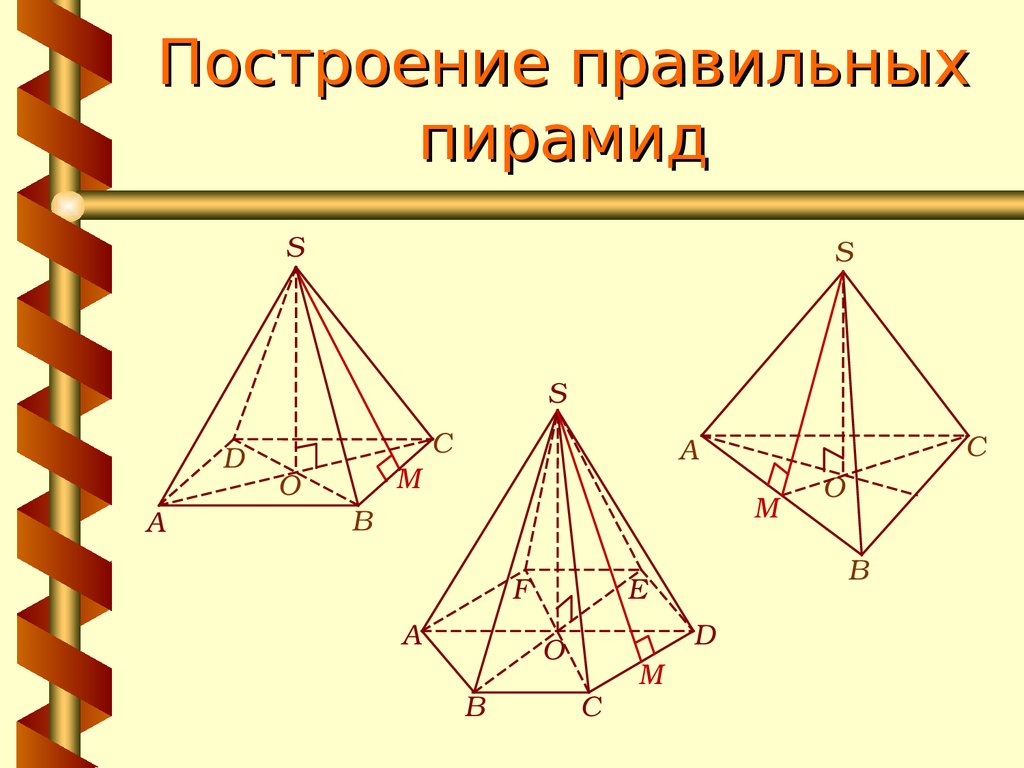
15. Построение правильных пирамид

S
S
S
D
А
M
O
C
С
А
M
В
F
A
B
В
E
D
O
C
M
O

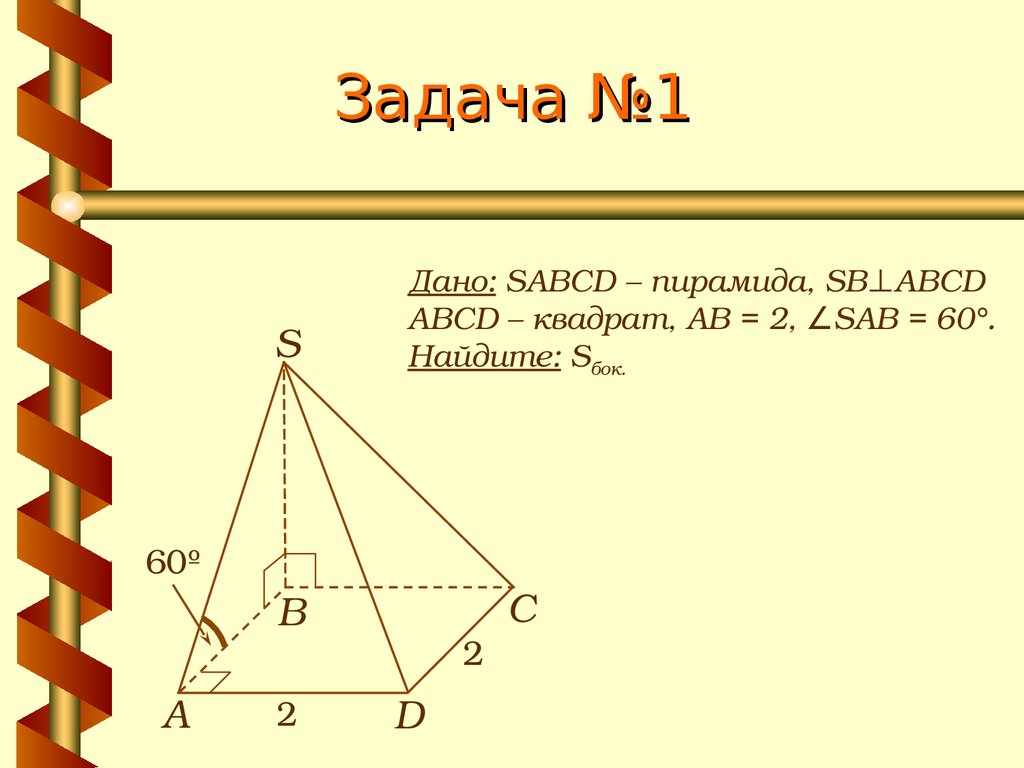
16. Задача №1

S
Дано: SABCD – пирамида, SB⊥ABCD
ABCD – квадрат, АВ = 2, ∠SAB = 60°.
Найдите: Sбок. 
60º
В
А
2
2
D
С

17. Задача №2

Дано: SABCD – пирамида, 
ABCD – ромб, АВ = BD, РABCD = 16, 
SO⊥(АВС), SO = 1.
Найдите: Sбок. 
S
1
В
С
В
O
А
H
D
А
С
O
D
H
М

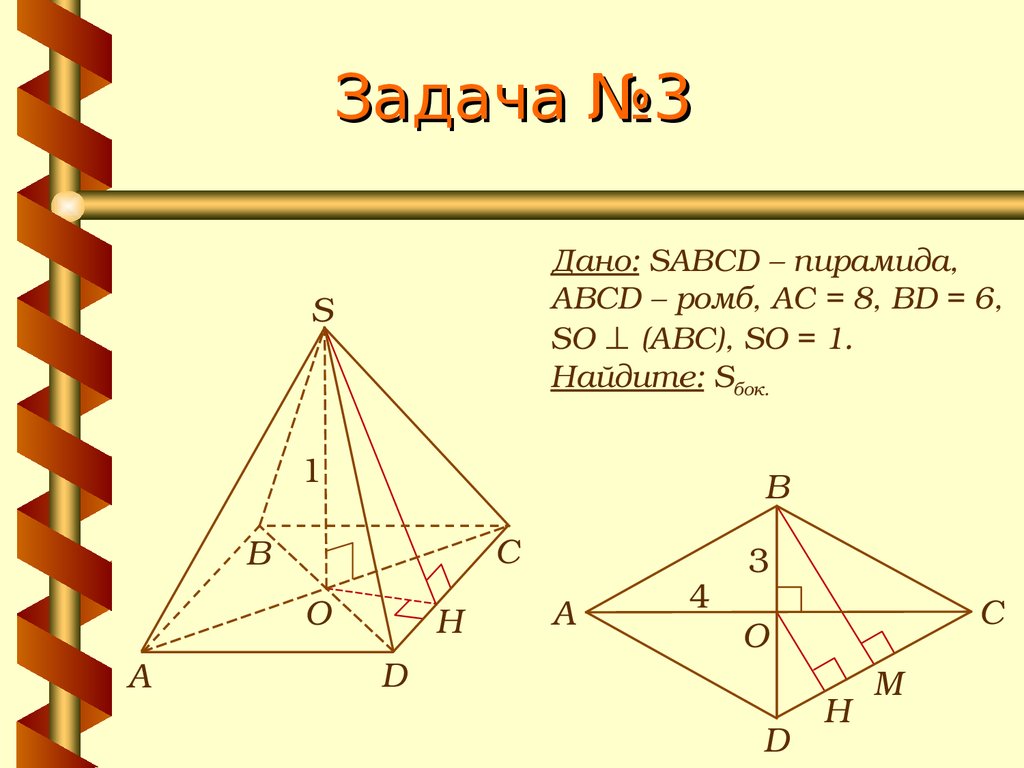
18. Задача №3

Дано: SABCD – пирамида, 
ABCD – ромб, АС = 8, BD = 6, 
SO ⊥ (АВС), SO = 1.
Найдите: Sбок. 
S
1
В
С
В
O
А
H
D
А
4
3
С
O
D
H
М

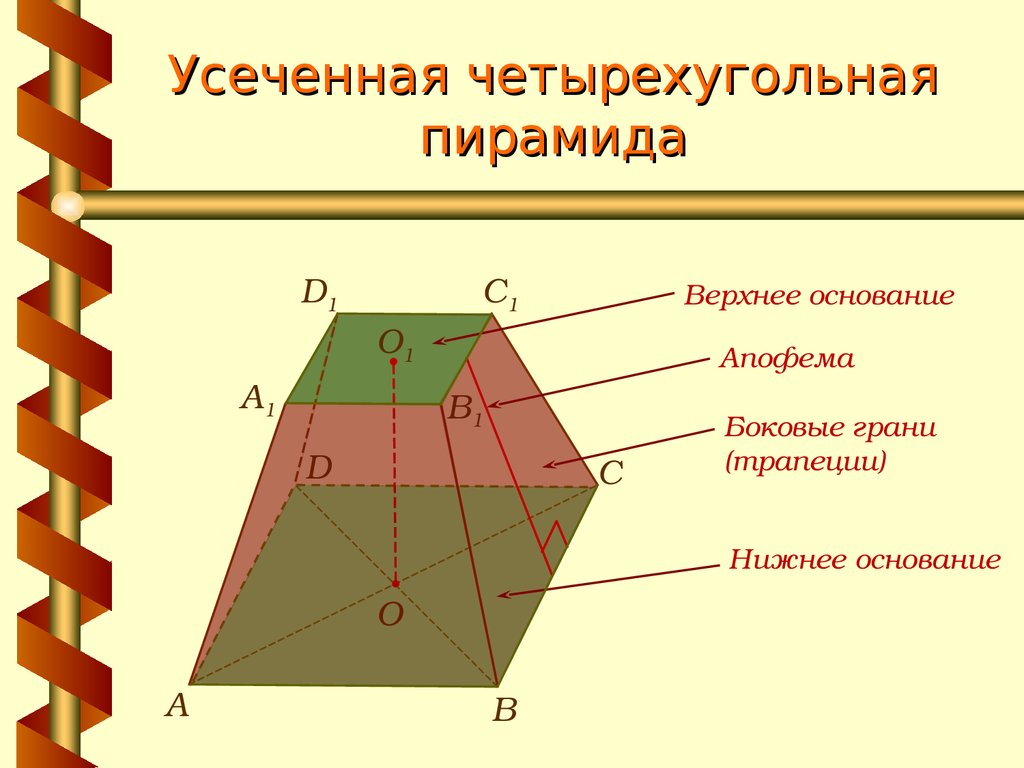
19. Усеченная четырехугольная пирамида

D1
C1
Верхнее основание 
О1
A1
Апофема 
B1
D
С
Боковые грани
(трапеции) 
Нижнее основание
О
А
В

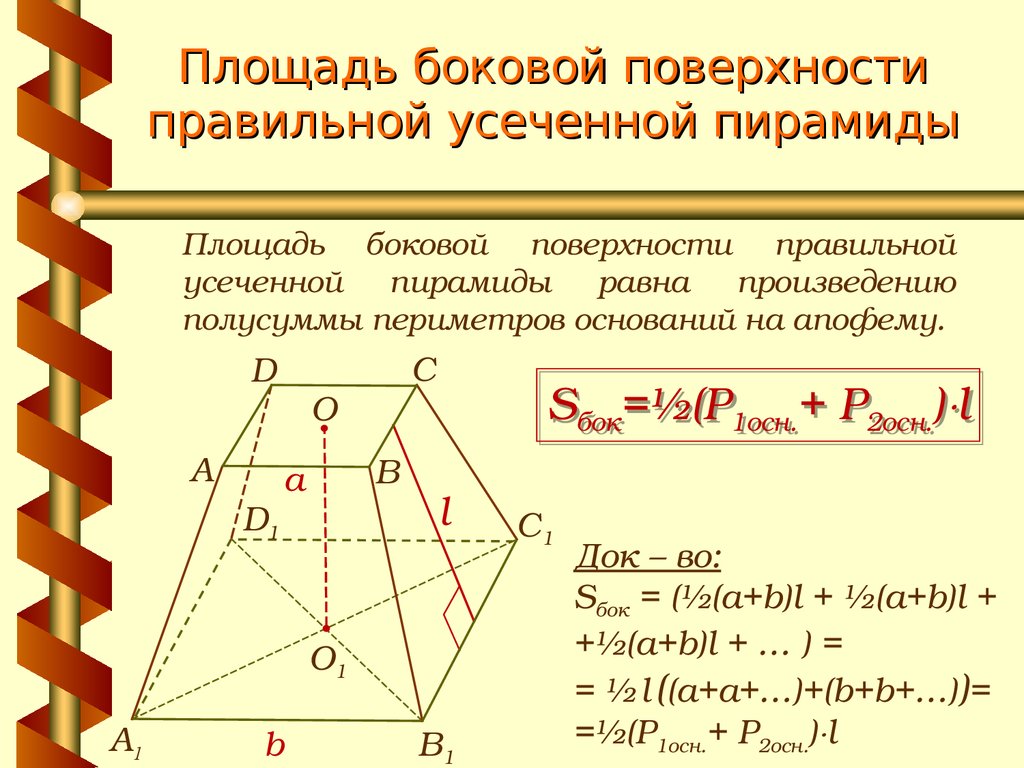
20. Площадь боковой поверхности правильной усеченной пирамиды

Площадь  боковой  поверхности  правильной 
усеченной  пирамиды  равна  произведению 
полусуммы периметров оснований на апофему.
D
A
D1
C
О
B
a
Sбок
=½(P1осн.
+ P2осн.
) l
бок
1осн.
2осн.
l
О1
А1
b
В1
С1
Док – во:
Sбок = (½(a+b)l + ½(a+b)l + 
+½(a+b)l + … ) = 
= ½ l ((a+a+…)+(b+b+…))= 
=½(P1осн.+ P2осн.) l

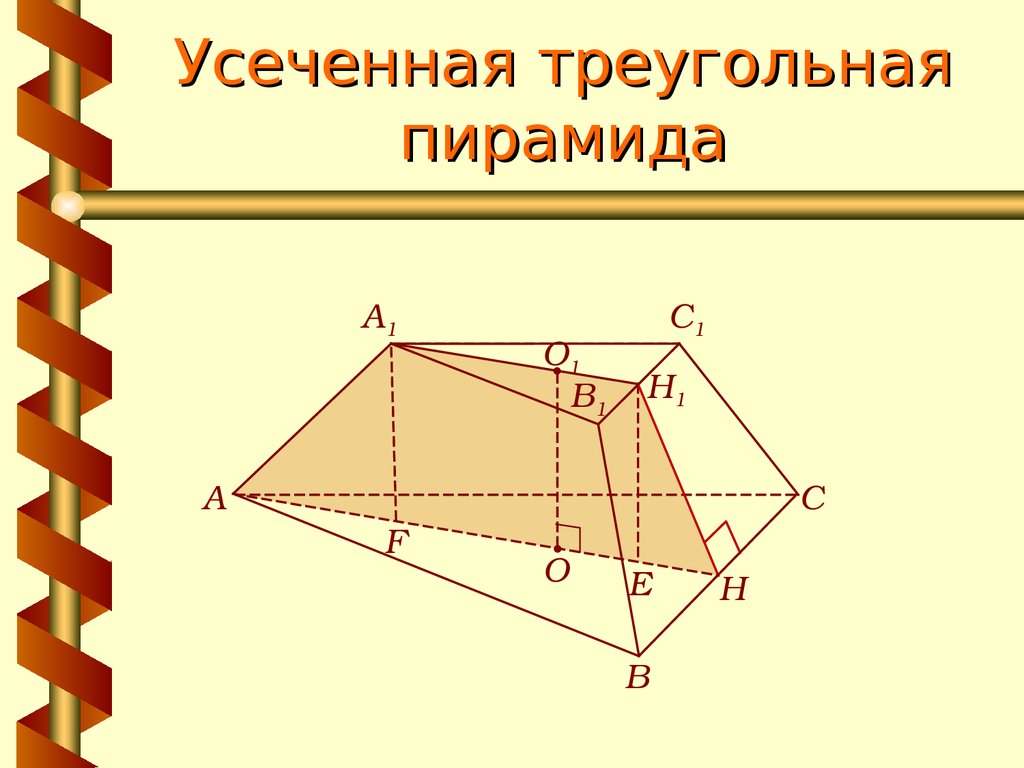
21. Усеченная треугольная пирамида

A1
О1
В1
C1
Н1
А
С
F
О
E
В
Н