Механика твердого тела. Момент силы относительно точки и оси вращения

1. МЕХАНИКА ТВЕРДОГО ТЕЛА Момент силы относительно точки и оси вращения

Лекция 5
МЕХАНИКА ТВЕРДОГО ТЕЛА
Момент силы относительно точки и
оси вращения
1

2.

М
О
r
h
А
F
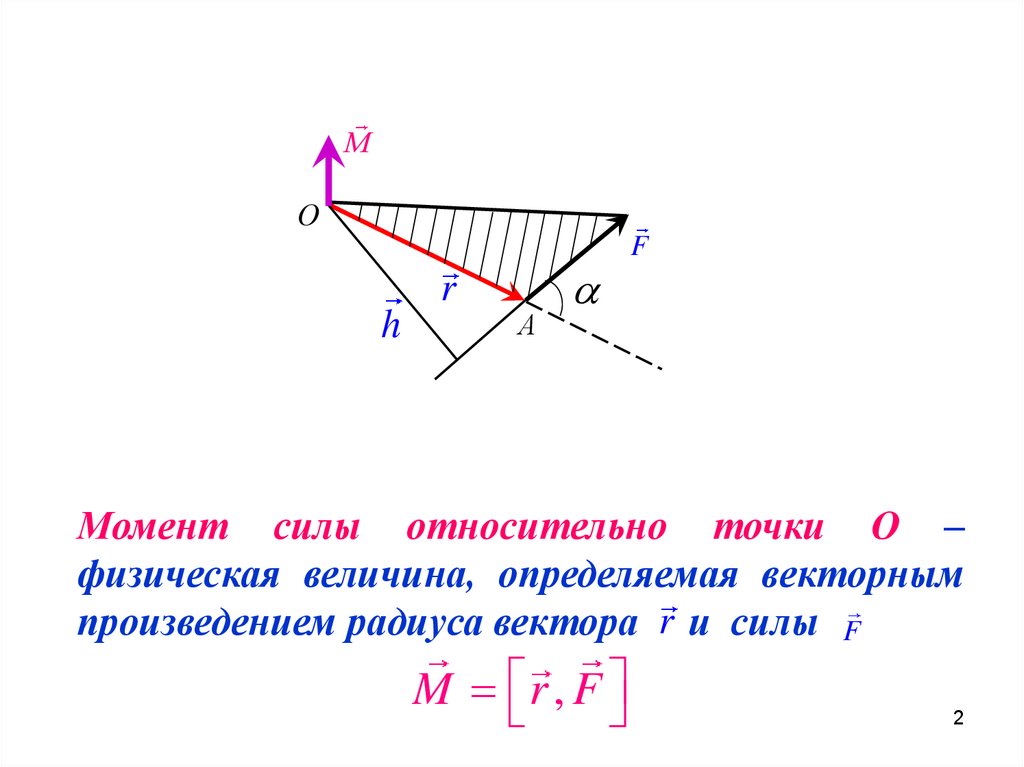
Момент силы относительно точки О –
физическая величина, определяемая векторным
произведением радиуса вектора r и силы F
M r , F
2

3.

Модуль момента силы:
M F r sin
r – радиус-вектор – вектор проведенный из
точки О в точку A приложение силы F ,
– угол между вектором r и F
Его направление определяется по правилу
правоходового винта или буравчика.
За
положительное
направление
вектора M ,
выбирается такое, что если смотреть с острия M ,
то кратчайший поворот от вектора r к вектору F
должен проходить против хода часовой стрелки. 3

4.

М
1
О
r
h
M F h
h r sin
M H M
À
F
2
F1
М1 М 2
F2
F1 l1 F2 l2
F1 F2
l2 l1
h – плечо силы, кратчайшее расстояние
(перпендикуляр) опущенный из точки О на
линию действия силы
4

5.

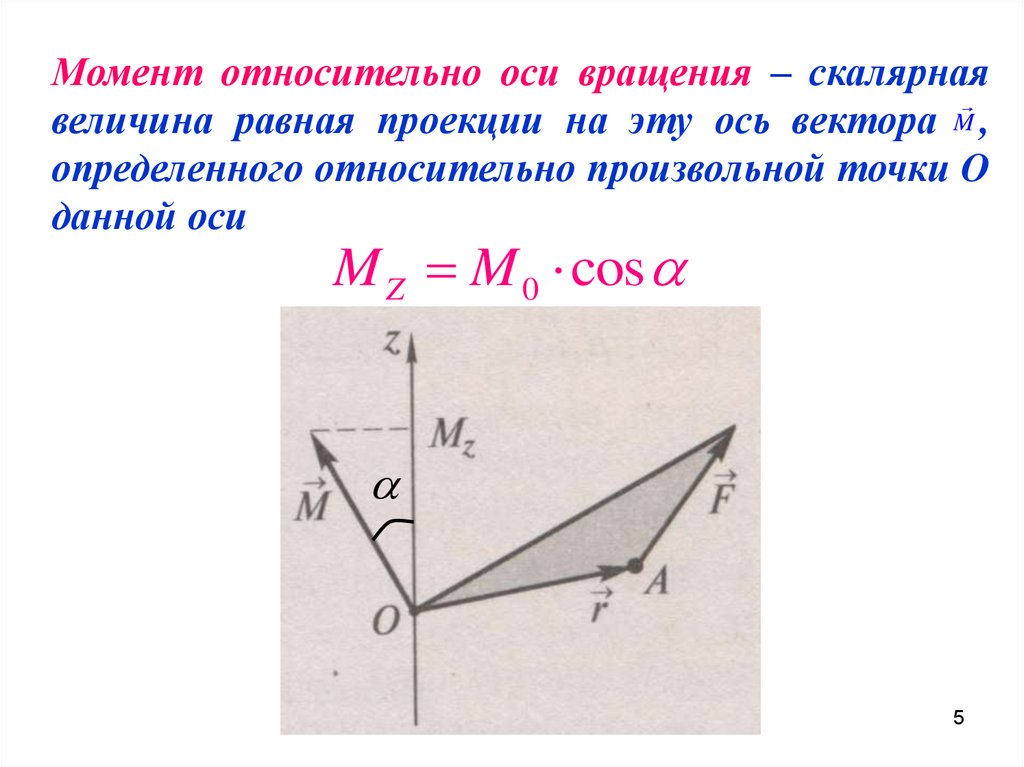
Момент относительно оси вращения – скалярная
величина равная проекции на эту ось вектора M ,
определенного относительно произвольной точки O
данной оси
M Z M 0 cos
5

6. Момент инерции относительно неподвижной оси вращения. Теорема Штейнера

6

7.

Момент инерции тела относительно оси –
скалярная величина, равная сумме произведений
элементарных масс на квадраты их расстояний до
рассматриваемой оси.
n
I m r
i 1
I mr
I r dm r dV
2
2
I кг м
2
i i
2
2
7

8.

Тело
Положение оси
Формула
Полый тонкостенный цилиндр
радиусом R
I m R2
Сплошной цилиндр или диск
радиусом R
I
1
m R2
2
Сплошной цилиндр или диск
радиусом R
I
1
m R2
4
Шар радиусом R
I
2
m R2
5
Прямой тонкий стержень
длиной l
I
Прямой тонкий стержень
длиной l
1
I m l2
3
1
m l2
12
8

9.

Теорема
Штейнера:
момент
инерции
относительно произвольной оси не проходящей
через центр тяжести тела равен сумме момента
инерции относительно оси проходящей через центр
масс параллельной данной оси и произведению
массы этого тела на квадрат расстояний между
этими осями.
I I C ma
2
9

10.

Пример: определить момент инерции стержня если
ось вращения проходит через один из его концов.
l
I I C ma 2
IC
1
ml 2
12
a
l
2
1 2 ml 2 4 2 1 2
I ml
ml ml
12
4
12
3
10

11. Момент импульса относительно точки или оси вращения

11

12.

L
О
p
r
h
А
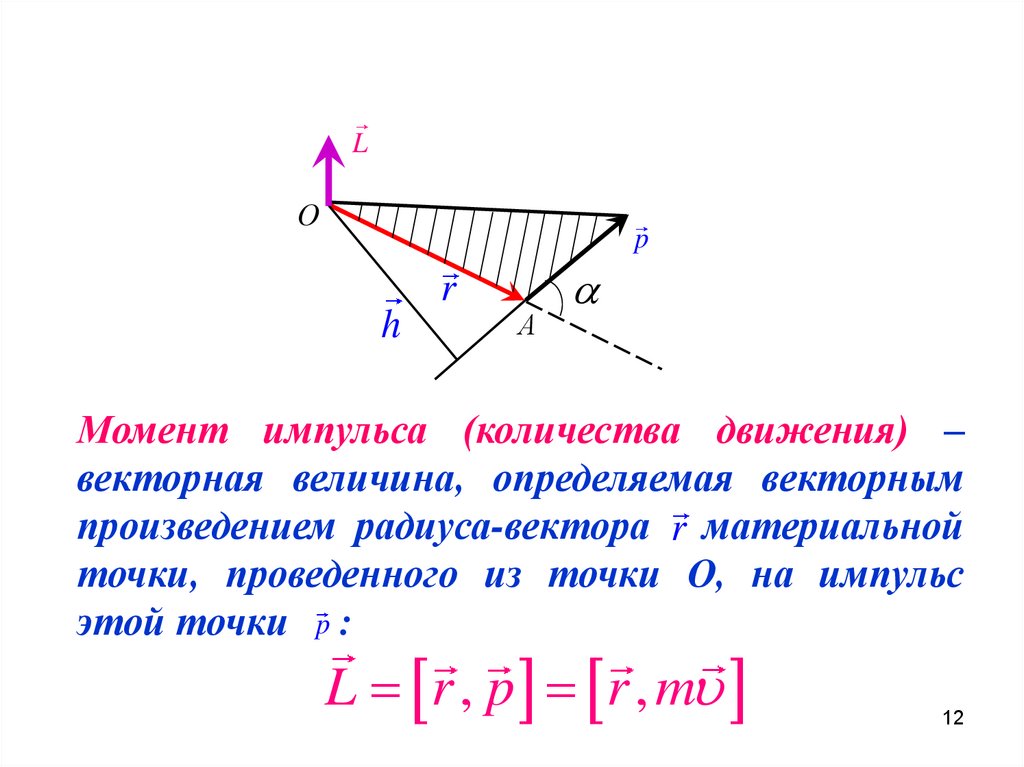
Момент импульса (количества движения) –
векторная величина, определяемая векторным
произведением радиуса-вектора r материальной
точки, проведенного из точки О, на импульс
этой точки p :
L r , p r , m
12

13.

Модуль момента импульса:
L r p sin
r – радиус-вектор – вектор проведенный из точки
О в точку A,
– угол между вектором r и p
Его направление определяется по правилу правого
винта или буравчика.
13

14.

L
О
p
r
h
А
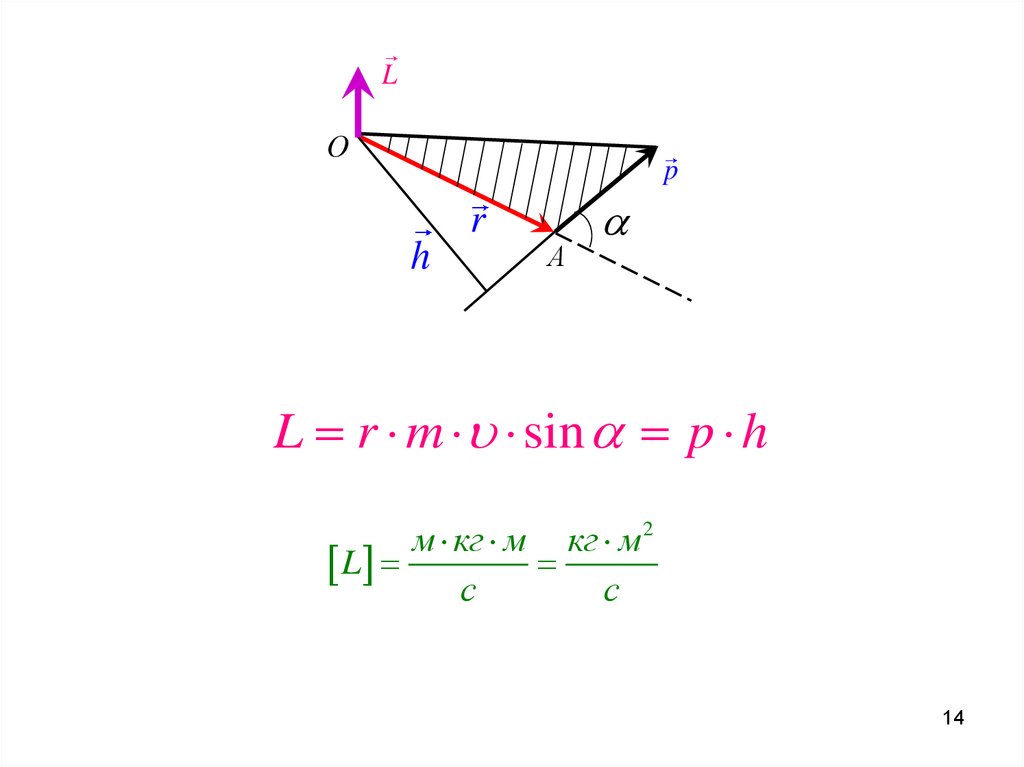
L r m sin p h
м кг м кг м 2
L
с
с
14

15.

Момент импульса относительно неподвижной оси:
скалярная величина, равная проекции на эту ось
вектора
момента
импульса,
определяемого
относительно точки О:
LZ L0 cos
n
LZ mi i ri
i 1
n
n
i 1
i 1
LZ mi ri 2 mi ri 2 I z
LZ I z
15

16. Работа и кинетическая энергия при вращательном движении. Основное уравнение динамики вращательного движения

16

17.

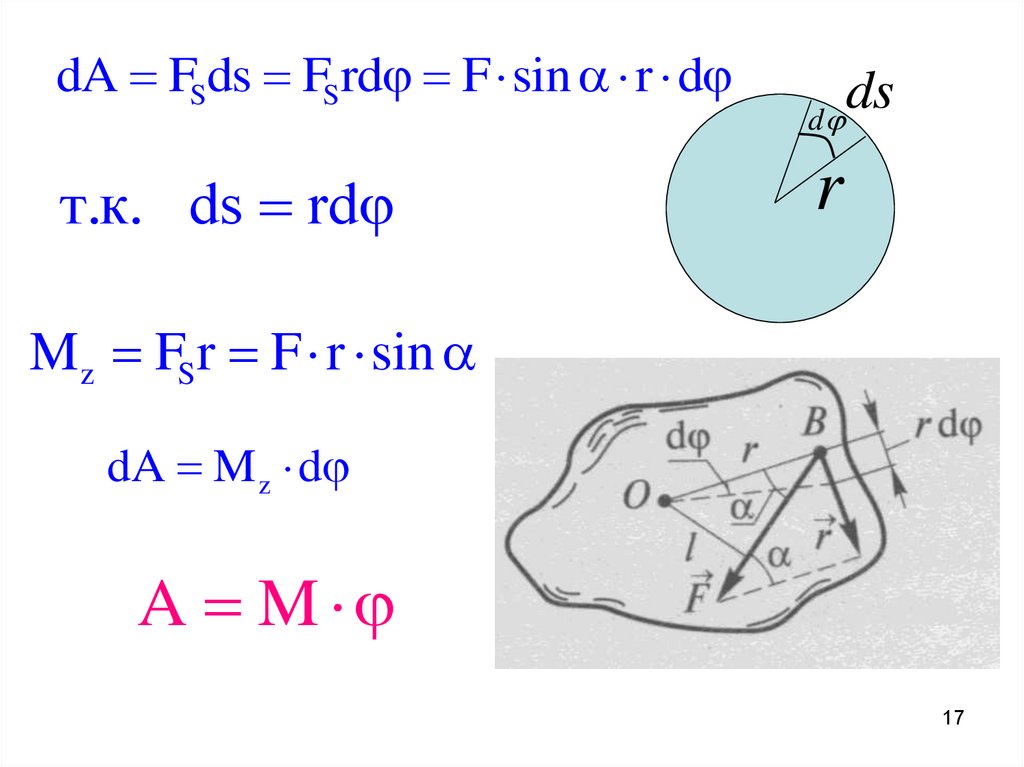
dA FSds FSrd F sin r d
т.к. ds rd
d
ds
r
M z FSr F r sin
dA M z d
A M
17

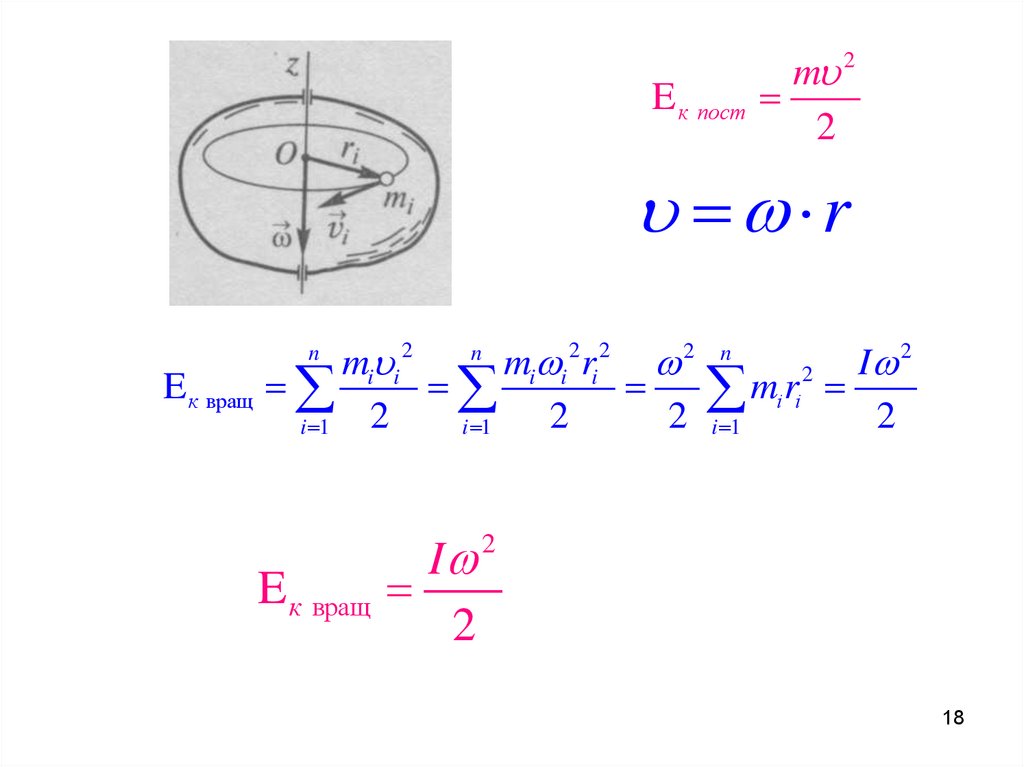
18.

m 2
E к пост
2
r
2
n
mi i 2
mi i 2 ri 2 2 n
I
2
E к вращ
m
r
i i
2
2
2 i 1
2
i 1
i 1
n
I 2
E к вращ
2
18

19.

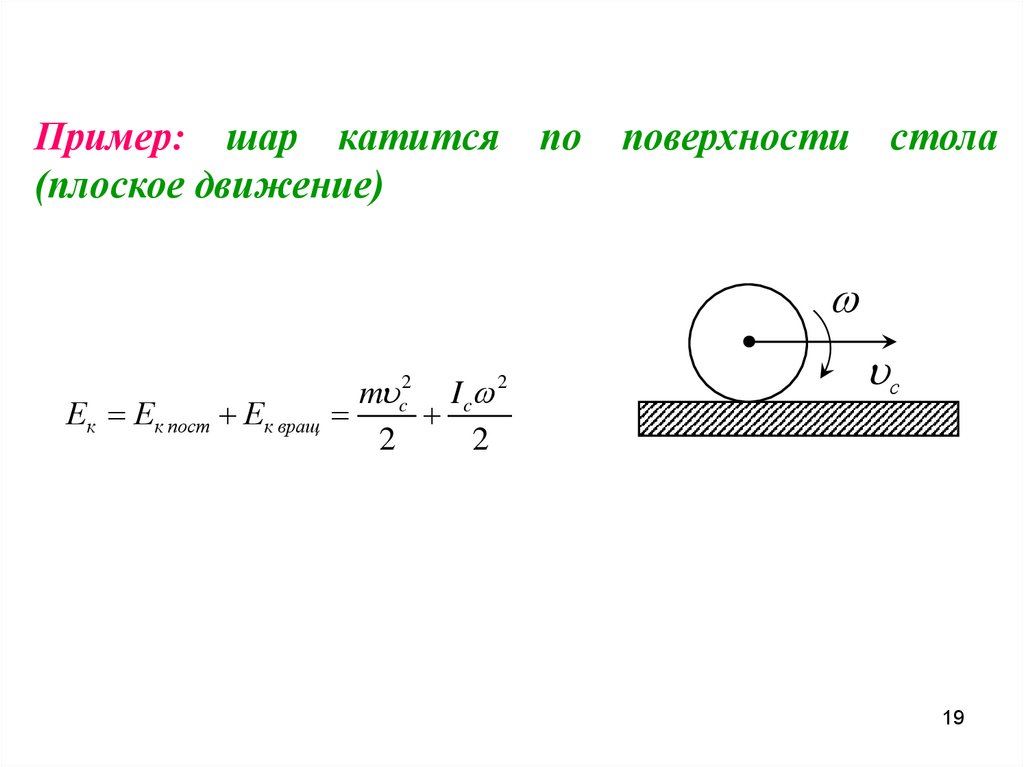
Пример: шар катится по поверхности стола
(плоское движение)
m c2 I c 2
Ек Ек пост Ек вращ
2
2
с
19

20.

dA dЕ к
Iz
dE ê d
Iz d
2
2
M z d I z d
d
d
Mz
Iz
dt
dt
d
dt
d
Mz I z I z
dt
основное
уравнение
динамики
вращательного движения
твердого тела
dL
M внеш
dt
20

21. Закон сохранения момента импульса

21

22.

dL
M внеш
dt
M внеш 0
dL
0
dt
L const
Момент
импульса
замкнутой
системы
сохраняется, т.е. не изменяется с течением
времени
I const
I1 1 I 2 2
22

23.

Закон сохранения момента импульса является
следствием симметрии пространства – его
изотропности.
Изотропность пространства – инвариантность
физических
законов
относительно
выбора
направлений осей координат системы отсчета
(относительно поворота замкнутой системы в
пространстве на любой угол).
23

24.

поступательное
вращательное
S
a
t2
at 2
S S 0 0t
2
0 0t
0 at
0 t
2 02 2aS
2 02 2
p
L
F
M
m
I
p m
L I
F
dp
dt
M внеш
2
dL
dt
F ma
M внеш I
m 2
Ек
2
m 2
Ек
2
A F S
A M
24