Похожие презентации:
Вращение твердого тела вокруг неподвижной оси
1. Вращение твердого тела вокруг неподвижной оси
Момент инерции материальнойточки
Момент инерции системы
материальных точек
Момент инерции твердого тела
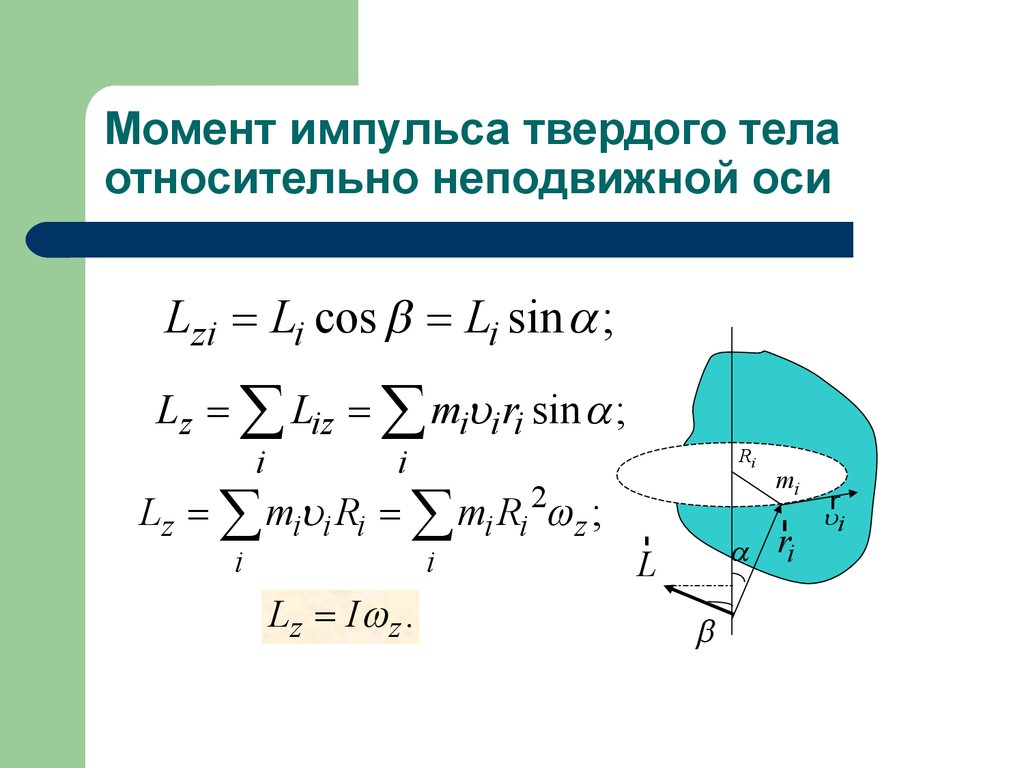
2. Момент импульса твердого тела относительно неподвижной оси
Рассчитаеммомент импульса
тела относительно оси,
r
представив тело как
L
систему материальных точек.
Ri
mi
r
a ri
b
r
ui
3. Момент импульса твердого тела относительно неподвижной оси
Lzi = Li cos b = Li sin a ;Lz = å Liz = å miui ri sin a ;
i
i
Lz = å miui Ri = å mi Ri 2w z ;
i
i
Lz = I w z .
Ri
mi
r
a ri
r
L
b
r
ui
4. Момент инерции
Момент инерции материальной точкиМомент инерции системы материальных точек
I = mR 2 .
I = å mi Ri .
2
i
Момент инерции твердого тела
2
2
I = ò r dm = ò r r dV .
m
V
5. Теорема Штейнера
Момент инерции относительно произвольной осиравен моменту инерции относительно оси,
параллельной данной и проходящей через центр
инерции тела, плюс произведение массы тела на
квадрат расстояния между осями
2
I = I c + ma .
6. Уравнение динамики вращательного движения
Основное уравнение динамики вращения твердоготела с неподвижной осью вращения легко
получить, как следствие, если
продифференцировать по времени уравнение
тогда
Lz = I w z ,
dw z
I
= M z , I bz = M z.
dt
7. Физический смысл момента инерции
Из уравнения динамики, в частности,видно, что момент инерции определяет
инерционные свойства твердого тела при
вращении: при одном и том же значении
момента сил тело с большим моментом
инерции приобретает меньшее угловое
ускорение.
8. Кинетическая энергия вращающегося тела
Рассмотрим тело как систему материальных точекmiui 2
Ek = Eki =
=
2
i
i
miw 2 Ri 2 I w 2
=
.
å
i
å
å
2
2
9. Работа внешних сил при вращении твердого тела
При вращении твердого тела вокруг неподвижнойоси работа внешних сил идет на приращение его
кинетической энергии
2
¶A = dEk ;
Iw
¶A = d (
) = I w z dw z ;
dj 2
Idw z = M z dt , w z =
¶A = M z dj .
dt
.
j
A = ò M z dj .
0
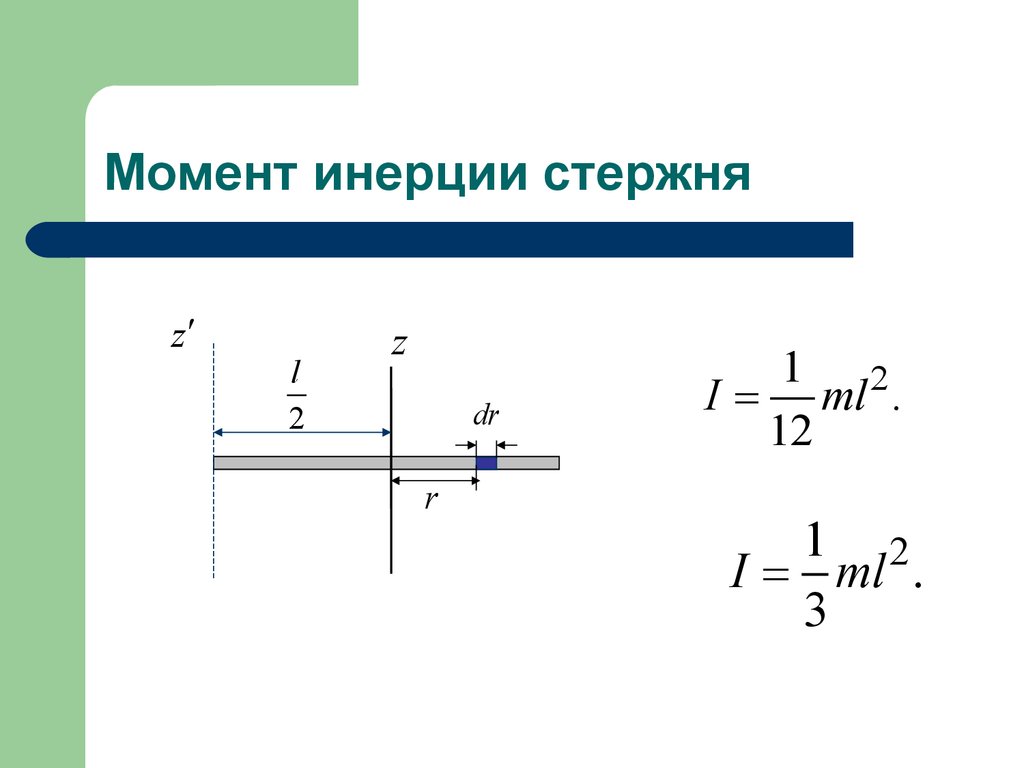
10. Момент инерции стержня
z¢l
2
z
dr
r
1 2
I = ml .
12
1 2
I = ml .
3
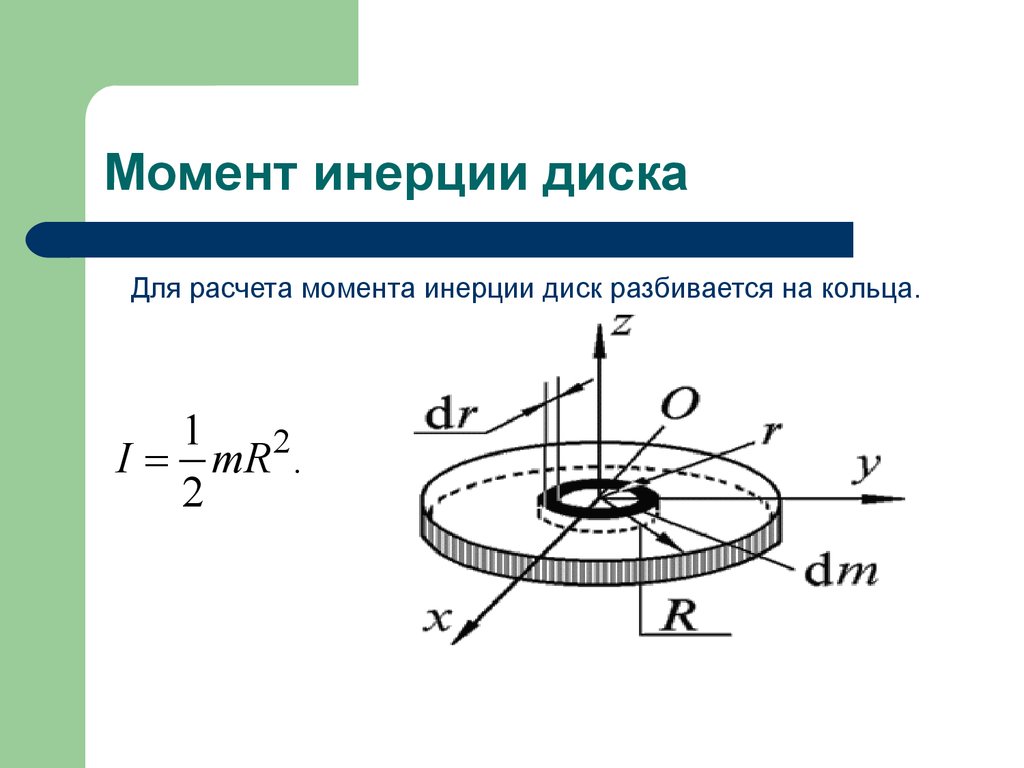
11. Момент инерции диска
Для расчета момента инерции диск разбивается на кольца.1
2
I = mR .
2
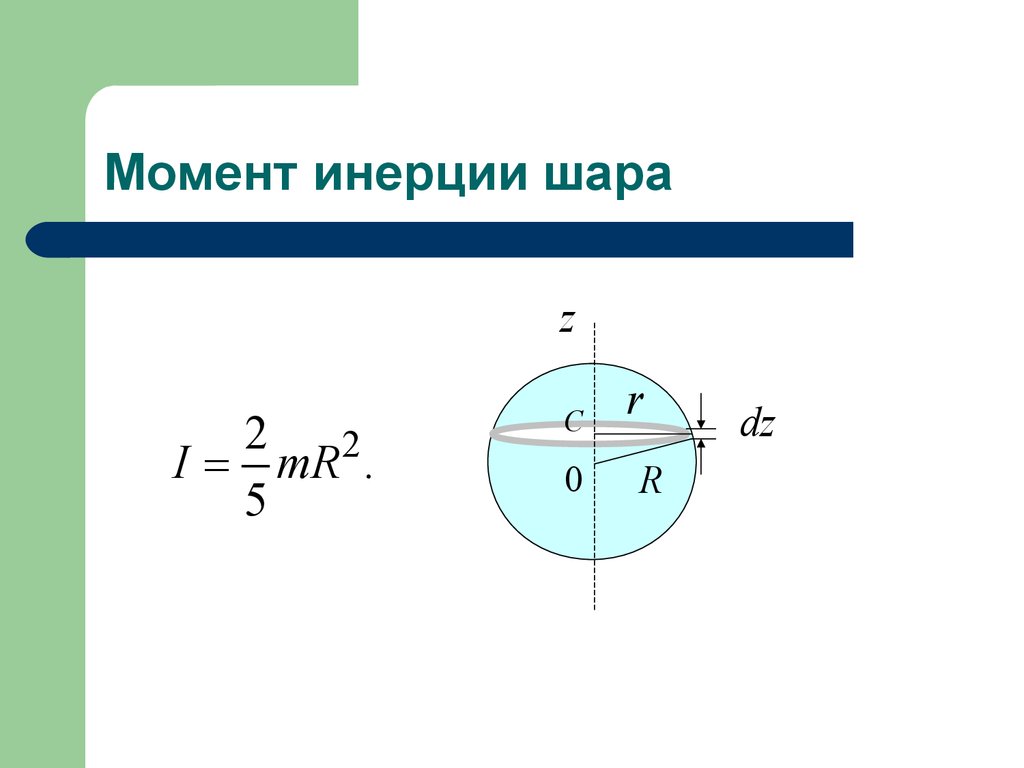
12. Момент инерции шара
z2
2
I = mR .
5
C
0
r
R
dz
13. Момент инерции шара
Разобьем шар на диски и выберем произвольныйдиск. z
C
0
r
R
dz
1
1
2
¶I = dmr = rp r 2 dzr 2 ;
2
2
1
¶I = rp r 4 dz.
2
14. Момент инерции шара
Перейдем к одной переменнойz
C
0
r
dz
R
R
r 2 = R2 - z 2.
1
8
4
2 2
4
I = rp ò ( R - 2 R z + z ) dz = rp R 5 .
2
15
-R
15. Момент инерции шара
Учтем, чтоr=
m
4 pR
3
3
.
Окончательно получим
2
2
I = mR .
5
16. Плоское движение
Плоским называется движение, прикотором все точки тела описывают
траектории в параллельных плоскостях
(качение цилиндра). При этом тело
участвует в двух движениях:
поступательном и вращательном.
17. Плоское движение
Динамические уравнения для плоского движения:r r
du
m
= F.
dt
dw z
I
= M z.
dt
18. Скорость и кинетическая энергия при плоском движении
r rr r
u = uc + [ w , r ] .
muc
I cw
Ek =
+
.
2
2
2
2














 Физика
Физика








