Движение. Развитие теоретического мышления на уроках

1.

Развитие теоретического мышления на уроках
математики.
ТЕМА: «ДВИЖЕНИЕ».
Работу выполняли ученики 9-«Б» класса.

2.

Алгоритм деятельности учащегося при создании проекта.
Выбор темы
Практическая
часть(подбор и
решение задач)
Защита
проекта
Работа с
информационными
ресурсами
Примеры
применения
Рефлексия
Осмысление и
прогнозирование
ожидаемого
результата
Создание
презентации
Моделирование
основной части
проекта
Разработка
критериев
оценивания

3.

КРИТЕРИИ ЗАЩИТЫ ПРОЕКТА.
1)Содержание проекта(теория)-2б.
2)Задачи-2б.
3)Защита-2б.
4)Оформление-1б.
5)Название-1б.
6)«Научность»-1б.

4.

ДВИЖЕНИЕ
Центральная
симметрия
Осевая
симметрия
Параллельный
перенос
Поворот

5.

Симметрия
Симметрия – это идея, с
помощью которой человек
веками пытался объяснить
и создать порядок, красоту
и совершенство.
Герман Вейль

6.

ОПРЕДЕЛЕНИЕ ЦЕНТРАЛЬНОЙ СИММЕТРИИ
Преобразование, переводящее каждую точку
А фигуры (тела) в точку А1, симметричную
ей относительно центра О, называется
преобразованием центральной симметрии
или просто центральной симметрией.

7.

ПРИМЕРЫ:

8.

ИНТЕРЕСНЫЕ ФАКТЫ
Термин «симметрия» придумал скульптор
Пифагор Регийский.
Древние греки полагали, что Вселенная
симметрична просто потому, что она
прекрасна.
Первую научную школу в истории человечества
создал Пифагор Самосский.
«Симметрия – это некая «средняя мера», считал Аристотель .
Римский врач Гален (2 в. н. э.) под симметрией
понимал покой души и уравновешенность.

9.

ИНТЕРЕСНЫЕ ФАКТЫ
Леонардо да Винчи считал, что главную
роль в картине играют пропорциональность
и гармония, под которыми он понимал
симметрию.
Альбрехт Дюрер (1471-1528 г.г.) утверждал,
что каждый художник должен знать способы
построения правильных симметричных
фигур.
Термин «симметрия» (σνμμετρυα, греч.) соразмерность, пропорциональность,
одинаковость в расположении частей.

10.

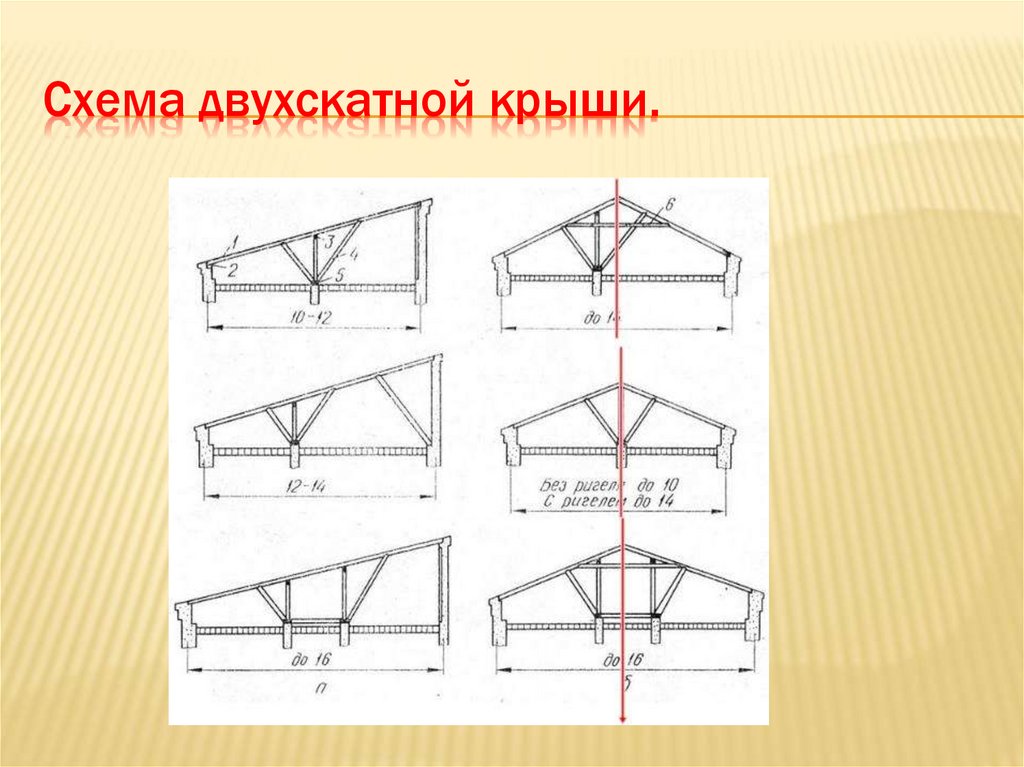
Схема двухскатной крыши.

11.

Зеркальная
симметрия

12.

Точки А и А1 называются симметричными относительно прямой l, если прямая l
перпендикулярна отрезку АА1 и проходит через его середину.
А
А1
А
А
А1
А1
l
l
l
Точка, принадлежащая оси
симметрии, симметрична
сама себе.
Преобразование фигуры, при котором каждой точке этой фигуры сопоставляется
точка, симметричная ей относительно заданной прямой l, называется осевой
с осью симметрией l.

13.

Осевая симметрия является движением, а следовательно,
симметричные фигуры равны.
При осевой симметрии
отрезок отображается на равный ему отрезок.

14.

Осевая симметрия является движением, а следовательно,
симметричные фигуры равны.
При осевой симметрии
треугольник отображается
на равный ему треугольник.

15.

Осевая симметрия является движением, а следовательно,
симметричные фигуры равны.
При осевой симметрии
параллелограмм отображается
на равный ему параллелограмм.

16.

Построение фигуры,
симметричной данной

17.

Построить
А1В1С1, симметричный
АВС относительно прямой i.
А1
С1
А
С
В1
В
i

18.

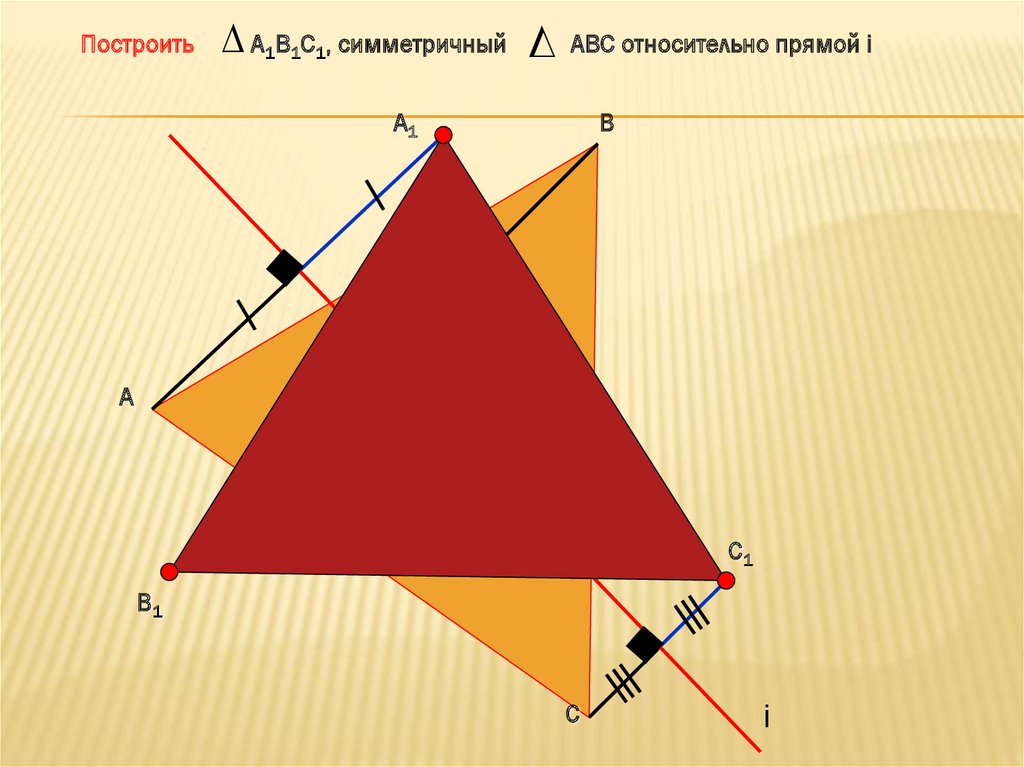
Построить
А1В1С1, симметричный
АВС относительно прямой i
А1
В
А
С1
В1
С
i

19.

Задача 1.
В прямоугольном треугольнике АВС ( C 90 ) медиана АМ=m проведена
к меньшему катету и образует с большим угол в 150. Найдите площадь
треугольника.
0
A
Решение:
1. Построим точку К, симметричную
точке М относительно прямой АС.
2. Имеем:
KAC MAC ,
S KAC S MAC ; S ABC
2 S AMC S KAM
B
2
1 2
m
0
m sin 30
.
2
4
K
С
M

20.

Встречи
с осевой симметрией

21.

Явление осевой симметрии
встречается часто в нашей жизни.
Буквы русского алфавита
имеют оси симметрии.

22.

А ВД ЕЖ З
К МН О П С
Т Ф ХШ Э Ю

23.

Существуют слова,
имеющие ось симметрии.
МАДАМ
КОК ФОКС
НОС

24.

25.

26.

27.

ЧТО ТАКОЕ
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС?
М1
Параллельным
переносом на вектор а
называется отображение
плоскости на себя, при
котором каждая точка М
отображается в такую
точку М1, что вектор ММ1
равен вектору а.
a
М
М

28.

СВОЙСТВА ПАРАЛЛЕЛЬНОГО
ПЕРЕНОСА
1.Параллельный перенос есть движение.
2.При параллельном переносе точки смещаются по
параллельным (или совпадающим) прямым на одно и то же
расстояние.
3.При параллельном переносе прямая переходит в
параллелельную прямую (или в себя).
4.Каковы бы ни были две точки X и X₁,существует, и притом
единственный, параллельный перенос, при котором точка X
переходит в точку X₁.
5.Преобразование,обратное параллельному переносу, есть
параллельный перенос. Композиция двух параллельных
переносов есть параллельный перенос.
6.При параллельном переносе в пространстве каждая плоскость
переходит либо в себя , либо в параллельную ей плоскость.

29.

ПОСТРОЕНИЕ
y
x

30.

А A1
C1
С
В
B1
a

31.

РЕШЕНИЕ:
Y
B
C
А
B₁
C₁
D А₁
D₁
X
В₂
С₂
Задача:
Построить трапецию, которая А₂
получится из данной трапеции
параллельным переносом на
вектор АD (на вектора 2CD).
D₂

32.

ЗАДАЧА
В каком месте следует построить мост MN через
реку, разделяющую две данные деревни А и В, чтобы
путь АМNВ из деревни А в деревню В был
кратчайшим? (берега реки считаются параллельными
прямыми, мост строиться перпендикулярно реке).

33.

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС В МУЗЫКЕ.
Легенда гласит о том, что проходя
мимо кузнецы Пифагор обратил
внимание на удивительно
мелодичное перестукивание
молотков кузнецов. Он взвесил их
молотки и получил соотношение
их веса 1:2 ;2:3; 3:4.
Дома он натянул струну на
«монохорде»( инструмент,
служащий для точного построения
музыкальных интервалов) и
зажимая струну в этих
отношениях получил те же
созвучия, что и кузнецы.

34.

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС В МОСТАХ
ПЕТЕРБУРГА
Длина Литейного моста 396 метров, ширина — 34 метра.
Масса металлических пролетных строений 5902 тонн
В районе моста Нева имеет наибольшую глубину — 24
метра.

35.

Троицкий мост соединяет центр Санкт-Петербурга и Петроградскую
сторону в непосредственной близости от Петропавловской
крепости.
Длина моста 582 метра ширина 24 метра
Масса стальных конструкций 11242 тонны

36.

Длина Дворцового моста 260 метров
Ширина 27,8 метра
Масса стальных конструкций 7770 тонн, в том числе 2800 тонн –
противовесы разводной части моста.

37.

Y
A(x;y)
B
C
A1(x+a;y+b)
B1
C1
0
X

38.

39.

40.

41.

42.

Параллельный
перенос

43.

44.

Поворот, а куда он уходит?
Поворо́т (враще́ние) — движение, при котором по крайней мере
одна точка плоскости (пространства) остаётся неподвижной.(Все точки
фигуры поворачиваются на один и тот же угол вокруг одной и той же точки –
центра поворота.)
Поворотная симметрия :
Поворот плоскости относительно центра О на данный угол, в данном
направлении определяется так: каждой точке X плоскости ставится в
соответствии такая точка X', что во-первых ОХ'=ОХ , во-вторых луч ОХ
откладывается от луча ОХ в заданном направлении. Точка О называется
центром поворота, а угол - углом поворота.
Х’
О
Х

45.

Поворот в движении.

46.

Центральная симметрия
M,
O
180°

47.

48.

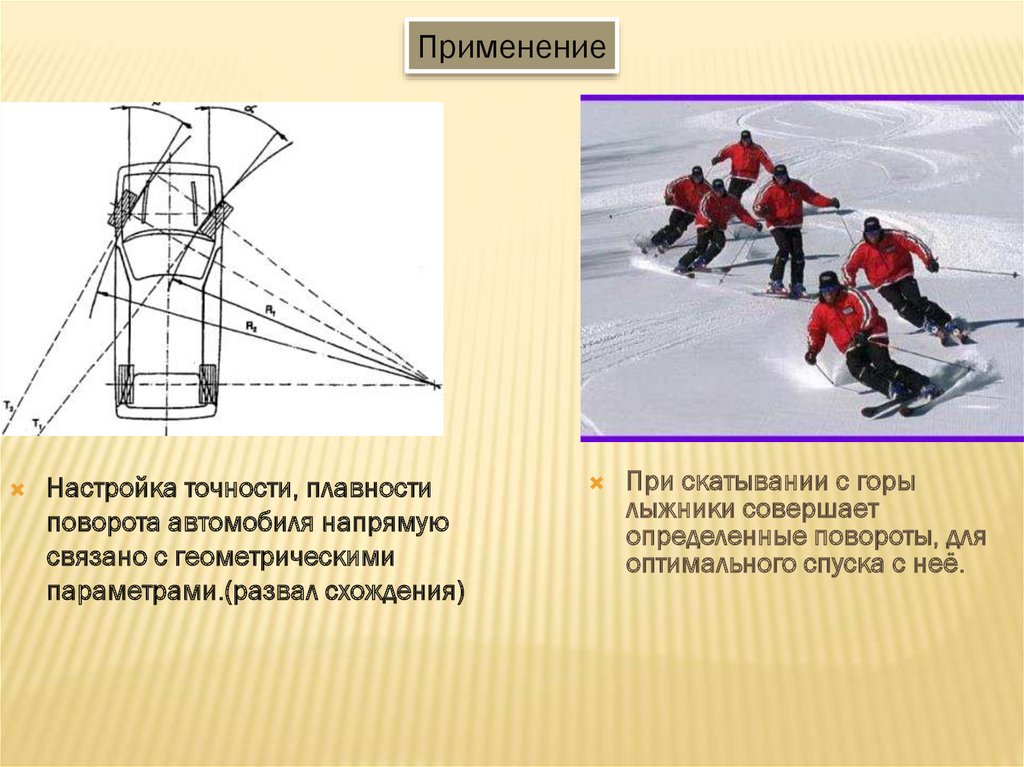
Применение
Настройка точности, плавности
поворота автомобиля напрямую
связано с геометрическими
параметрами.(развал схождения)
При скатывании с горы
лыжники совершает
определенные повороты, для
оптимального спуска с неё.

49.

Задача №1169
В
С
О
А
D
Дано: ABCD- квадрат, AC и BD диагонали , (●)O -пересечение
диагоналей.
Докажите: при повороте
квадрата вокруг (●)O на угол
90° квадрат отображается на
себя
Доказательство:
Так как AC перпендикулярна BD, то AC перейдет в BD. А если AO
равна OC и BO равна OD, то A→B, B→C, C→D, D→A отсюда ABCD
→ ABCD.

50.

Спасибо за внимание.