Похожие презентации:
Теория Гинзбурга - Ландау
1.
Теория Гинзбурга – ЛандауА.С.Мельников
2.
Феноменологическая теория Ландау для фазовыхпереходов II рода. Параметр порядка. Примеры.
План
Волновая функция электронной системы в нормальном
металле и сверхпроводнике.
Уравнения на параметр порядка.
Параметр порядка для сверхпроводящих электронов.
Уравнения Гинзбурга – Ландау.
Граничные условия.
Квантование магнитного потока.
3.
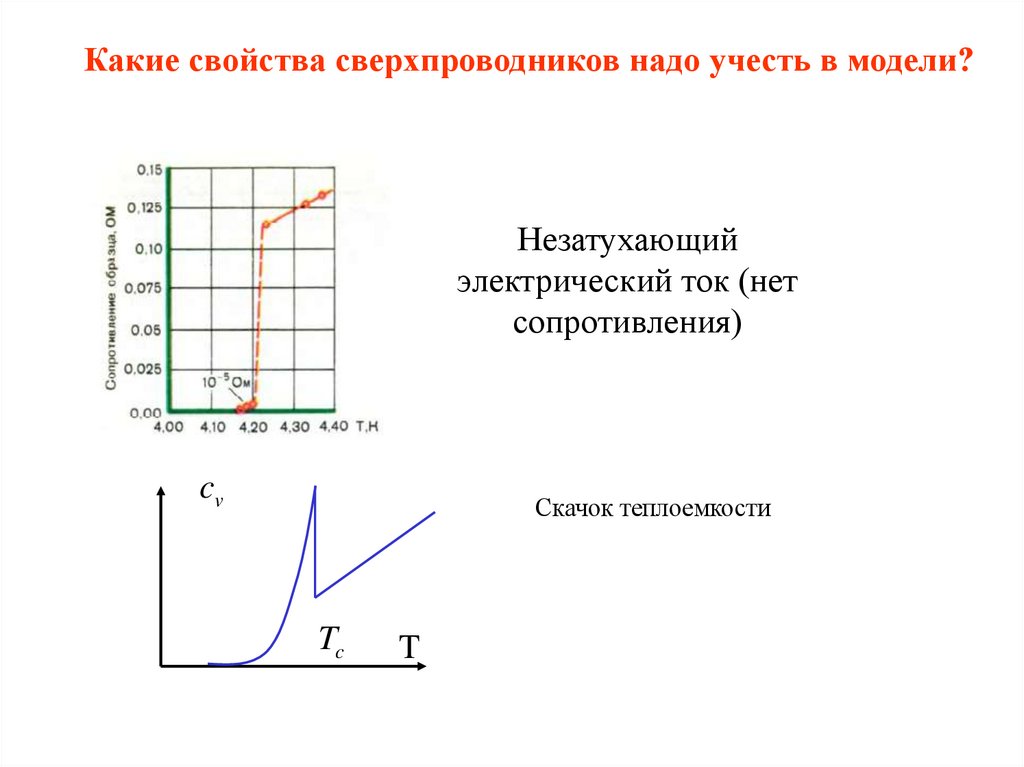
Какие свойства сверхпроводников надо учесть в модели?Незатухающий
электрический ток (нет
сопротивления)
cv
Скачок теплоемкости
Tc
T
4.
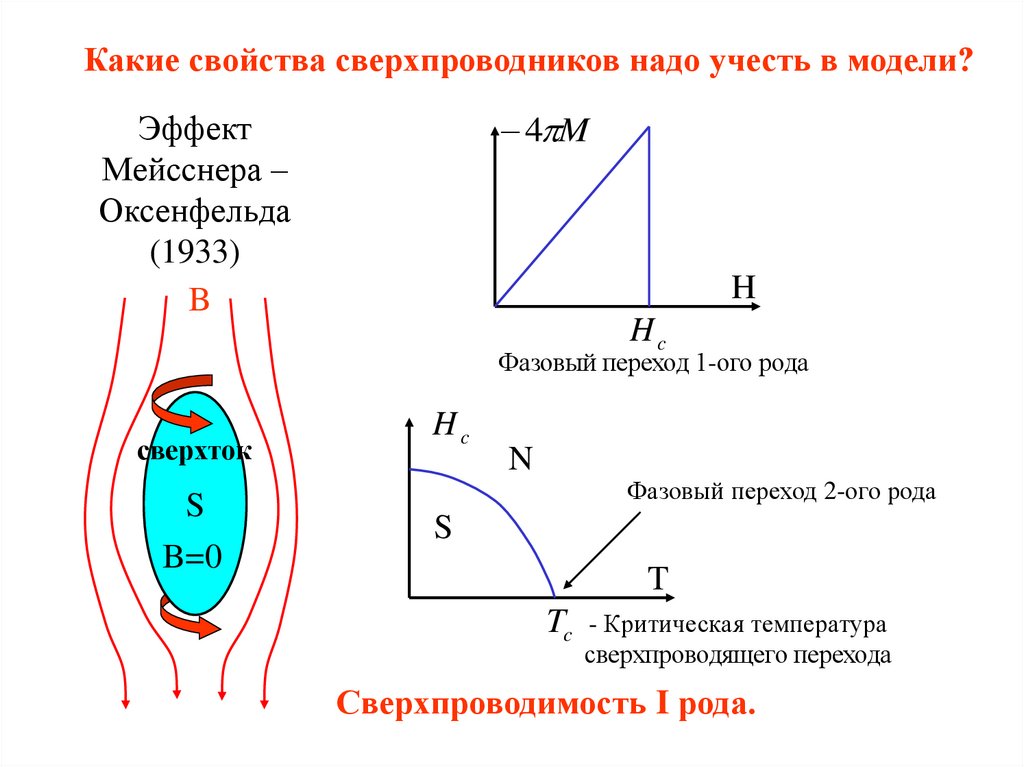
Какие свойства сверхпроводников надо учесть в модели?4 M
Эффект
Мейсснера –
Оксенфельда
(1933)
B
H
Hc
Фазовый переход 1-ого рода
сверхток
S
B=0
Hc
N
Фазовый переход 2-ого рода
S
T
Tc - Критическая температура
сверхпроводящего перехода
Сверхпроводимость I рода.
5.
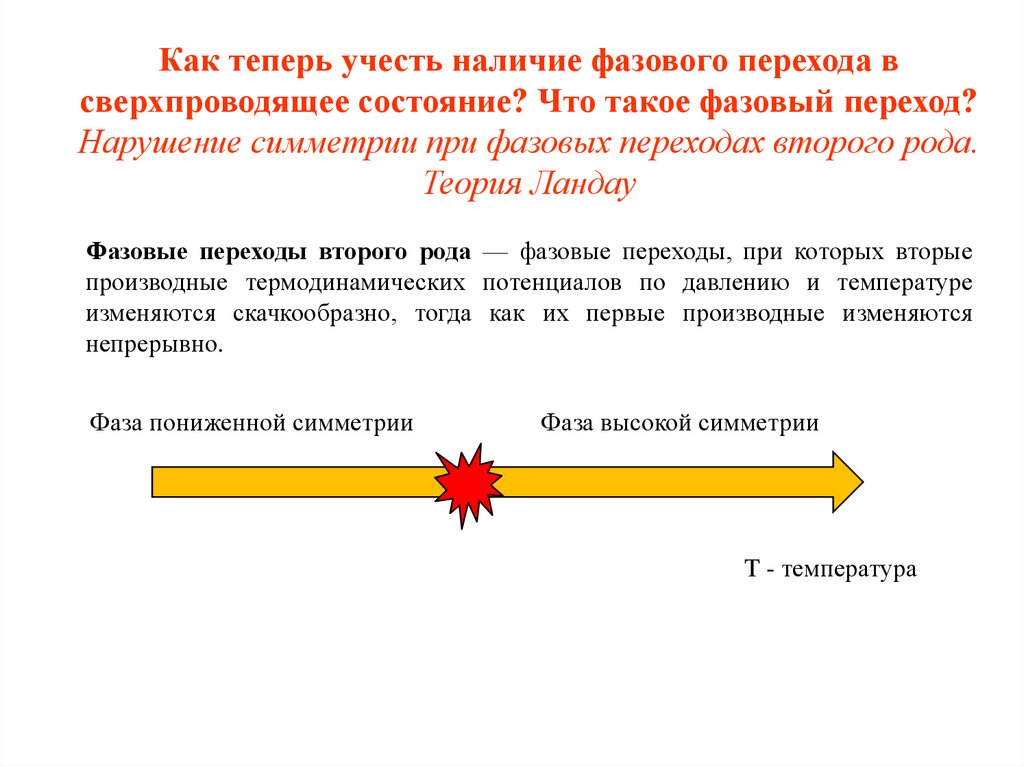
Как теперь учесть наличие фазового перехода всверхпроводящее состояние? Что такое фазовый переход?
Нарушение симметрии при фазовых переходах второго рода.
Теория Ландау
Фазовые переходы второго рода — фазовые переходы, при которых вторые
производные термодинамических потенциалов по давлению и температуре
изменяются скачкообразно, тогда как их первые производные изменяются
непрерывно.
Фаза пониженной симметрии
Фаза высокой симметрии
T - температура
6.
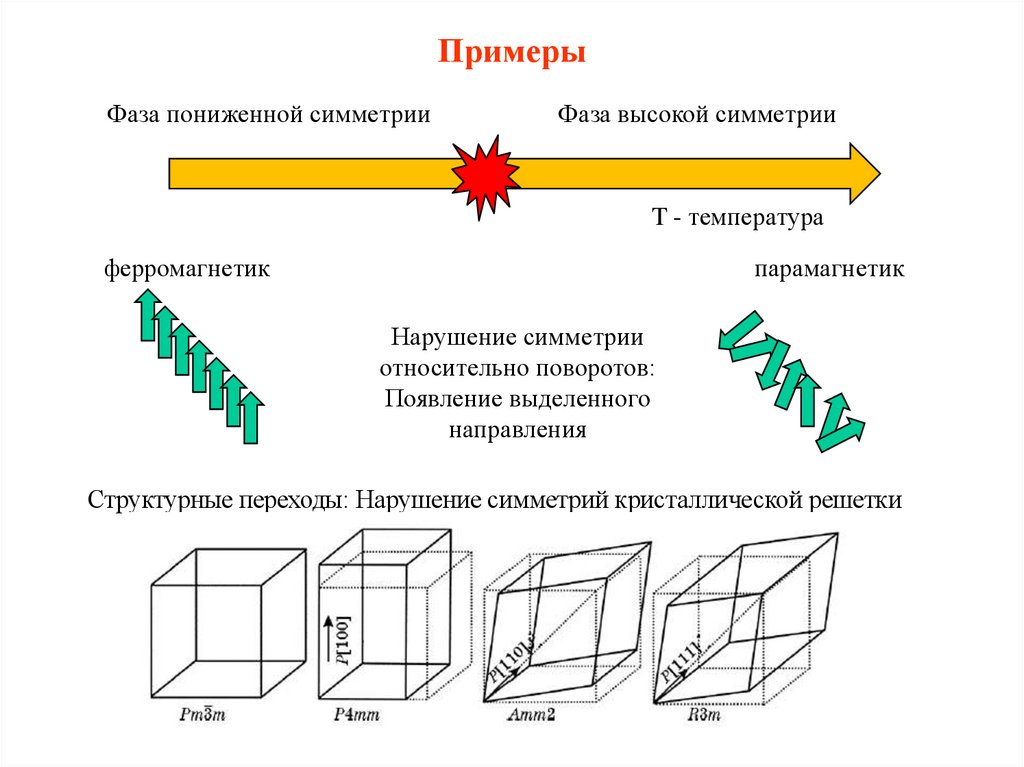
ПримерыФаза пониженной симметрии
Фаза высокой симметрии
T - температура
ферромагнетик
парамагнетик
Нарушение симметрии
относительно поворотов:
Появление выделенного
направления
Структурные переходы: Нарушение симметрий кристаллической решетки
7.
Параметр порядкаФерромагнетизм:
Структурный переход:
Сверхпроводящий
переход?
M
d
Концентрация
сверхпроводящих
электронов?
ns
8.
Теория Ландау: разложение свободной энергии в ряд попараметру порядка
F Fn ans bns2 dV
F
a (T Tc )
T Tc
ns
T Tc
Проблема: как включить магнитное поле в теорию
9.
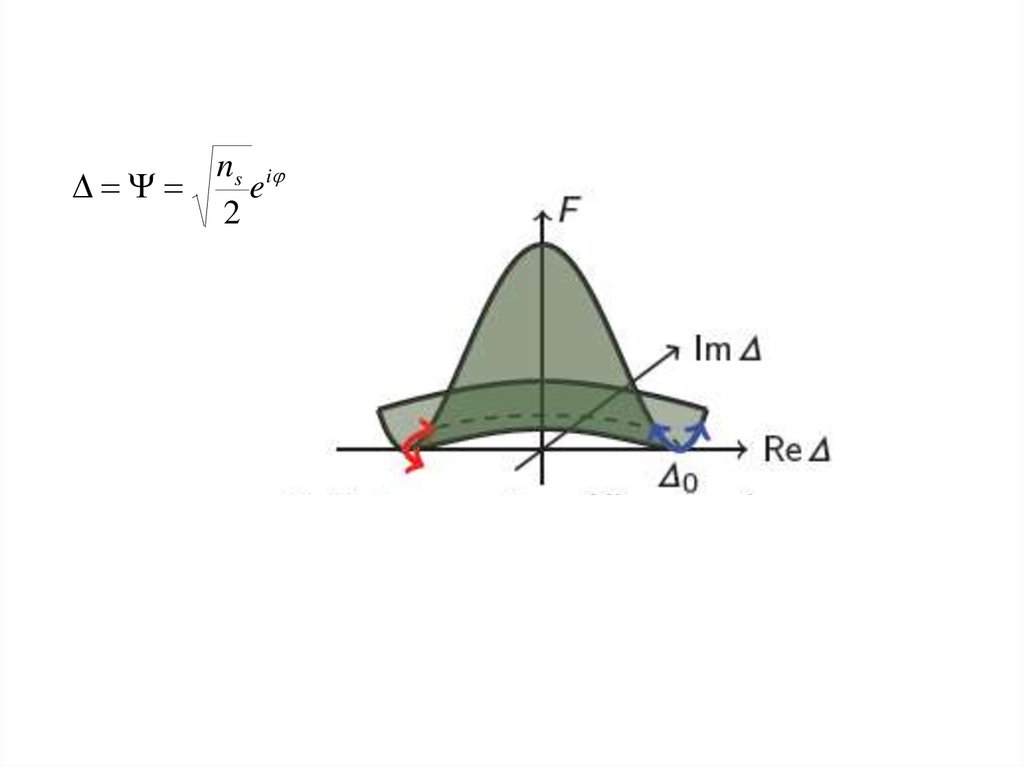
Феноменологическая теориясверхпроводимости Гинзбурга-Ландау
Параметр порядка
ns i
e
2
Плотность
сверхпроводящих
электронов
Для медленных изменений параметра порядка в пространстве:
Свободная энергия
2
b 4
2
2
F Fn
a dV
2
4m
Свободная энергия
нормального состояния
Равновесный параметр порядка в
однородном сверхпроводнике
a (T Tc )
2
(Tc T )
b
10.
n s ie
2
11.
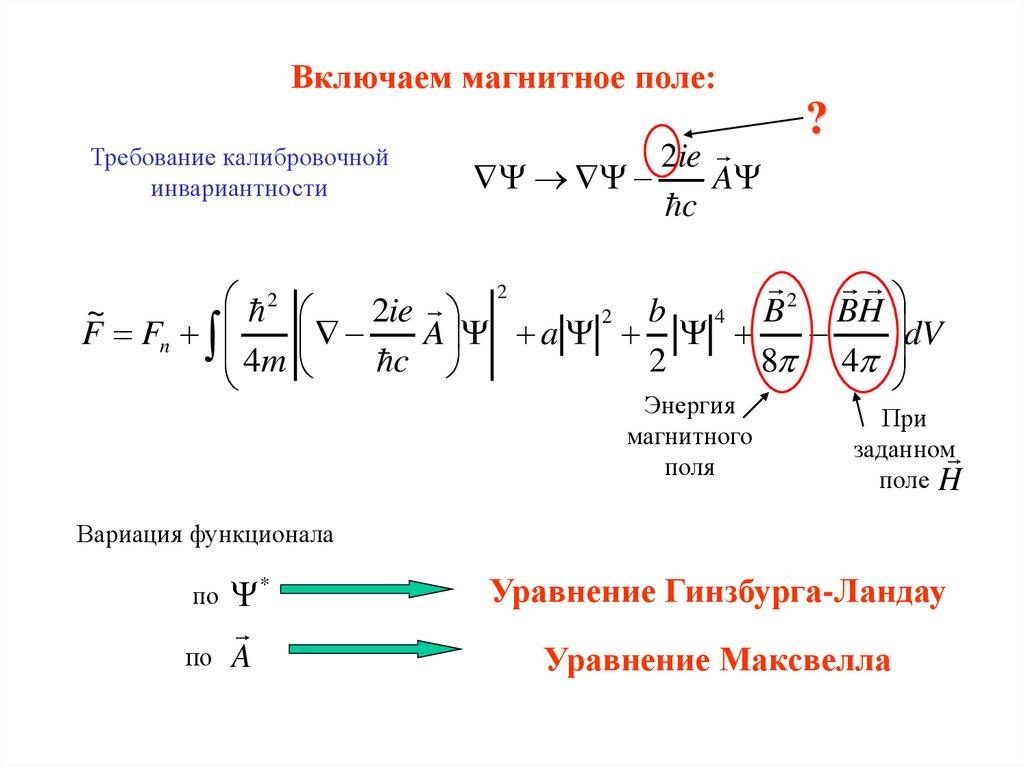
Включаем магнитное поле:Требование калибровочной
инвариантности
2ie
A
c
?
2
2
2
2
ie
b
B
B
H
~
2
4
dV
F Fn
A a
4m
c
2
8
4
Энергия
магнитного
поля
При
заданном
поле H
Вариация функционала
по
по A
*
Уравнение Гинзбурга-Ландау
Уравнение Максвелла
12.
22
2
2
ie
b
B
2
4
dV
F Fn
A a
4m
c
2
8
B B
1
dV
F rotM A
4 M B BdV
4
4
BH
~
dV
F F
4
BdH
~
dV
dF SdT
4
13.
Q. Какая симметрия нарушена присверхпроводящем переходе?
A. Калибровочная
Q. Почему в функционале нет нечетных
степеней пси-функции и высших
производных?
A. Соображения симметрии + малость
нелокальных эффектов
Q. Как выбрать знаки коэффициентов функционала?
A. Соображения устойчивости
14.
Волновая функция электронной системыв нормальном металле и
сверхпроводнике.
1
N!
1 ( 1 ) 1 ( 2 ) ... ... 1 ( N )
2 ( 1 ) 2 ( 2 ) ... ...
...
...
...
N ( 1 )
...
...
...
... ...
...
... ...
...
... ... N ( N )
(r , s)
Aˆ ( 1 , 2 ) ( 3 , 4 ) ( 5 , 6 )...
А если число частиц нечетно?
А куда в ГЛ теории пропала
вторая координата?
15.
22ie
2
A a b 0
4m
c
2
4
rotB
j
c
I-S
2
ie *
2
e
2
*
j
A
2m
mc
e 2 2e
j
A
m
c
e 2 ns
j
A
mc
Граничные
условия
Уравнение Лондонов
2ie
n
A 0
c
N-S
0
16.
Сверхтекучаяскорость
2e
j ensVs ens
A
2m
c
17.
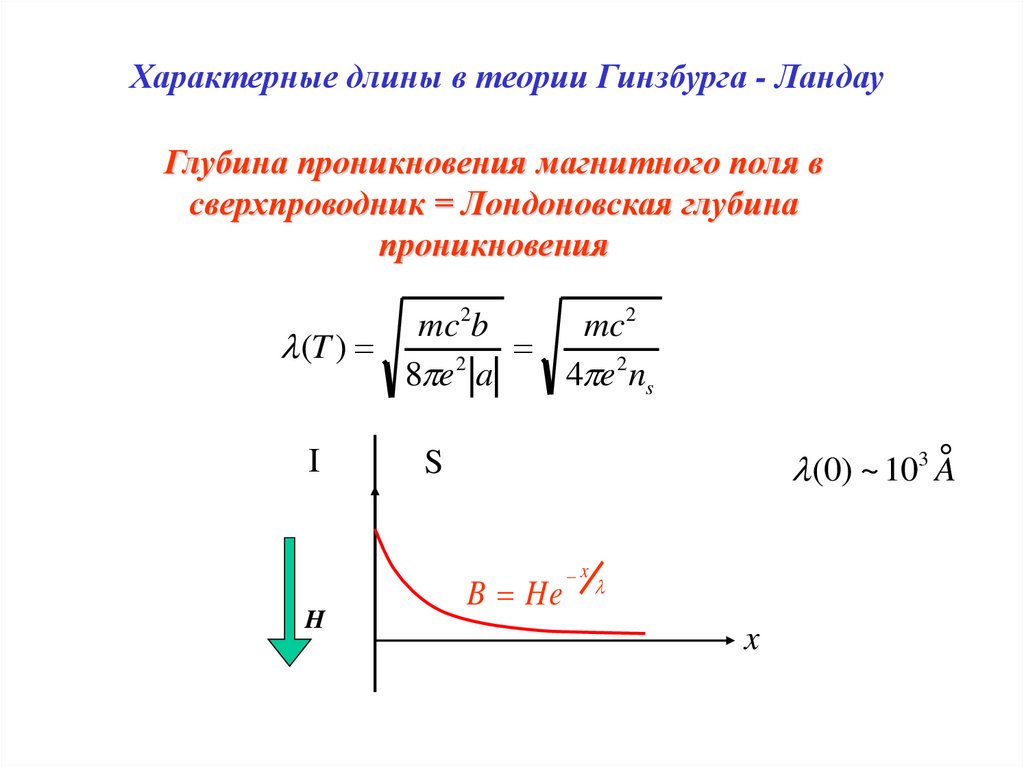
Характерные длины в теории Гинзбурга - ЛандауГлубина проникновения магнитного поля в
сверхпроводник = Лондоновская глубина
проникновения
mc2b
mc2
(T )
2
8 e a
4 e 2 ns
I
H
(0) ~ 103 A
S
B He
x
x
18.
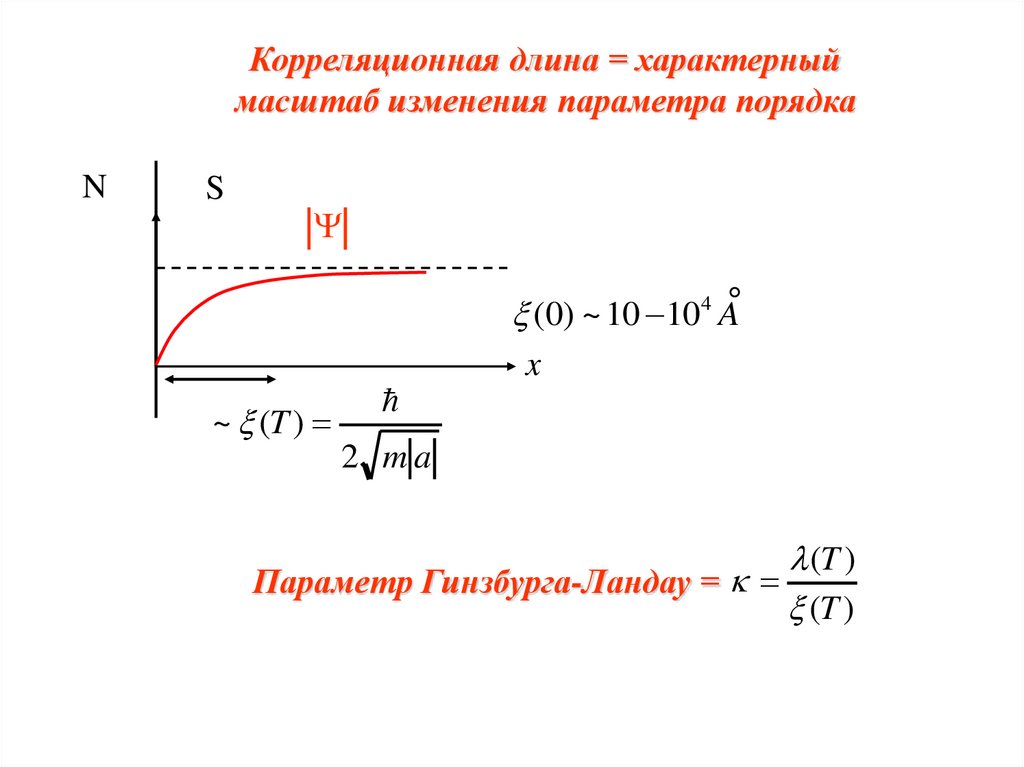
Корреляционная длина = характерныймасштаб изменения параметра порядка
N
S
(0) ~ 10 104 A
x
~ (T )
2 ma
Параметр Гинзбурга-Ландау =
(T )
(T )
19.
Термодинамическое критическое поле.Квант магнитного потока
a (Tc T )
b
b
2
2
2 (Tc T ) 2
H cm
Fs Fn V
V
2b
8
4
H cm
b
2
12
0
(Tc T )
2 2
c
0
2 10 7 Гс см 2
e
20.
Квантование магнитного потокаe 2 2e
j
A
m
c
j 0
2e
Ad 2 n 0
c
2e
2 n 0
c
n 0
21.
Обобщения теории ГЛCверхпроводники с анизотропным или
многокомпонентным параметром порядка
Вектор или тензор
Неустойчивости и высшие производные
Cлоистые сверхпроводники. ВТСП
Анизотропия. Тензор эффективных масс.
22.
Задачи 2aНайти критическую температуру появления сверхпроводимости в диске в
перпендикулярном магнитном поле. То же для пластины в форме квадрата (в
перпендикулярном поле).
найти критическую температуру появления сверхпроводимости в магнитном
поле в анизотропном сверхпроводнике (с тензором масс в теории ГЛ), при
произвольной ориентации поля относительно оси анизотропии. Анизотропия –
одноосная.
Решить задачу мейсснеровской экранировки в сверхпроводнике с одноосной
анизотропией тензора масс в теории ГЛ
Найти поле разрушения сверхпроводимости в полом цилиндре в магнитном
поле, перпендикулярном оси цилиндра.
Найти критическую температуру появления сверхпроводимости на плоскости
двойникования, в модели, предполагающей локальное повышение Тс на
плоскости.
Найти амплитуду сверхпроводящего зародыша в бислое сверхпроводник –
нормальный металл (вблизи температуры зарождения сверхпроводимости).





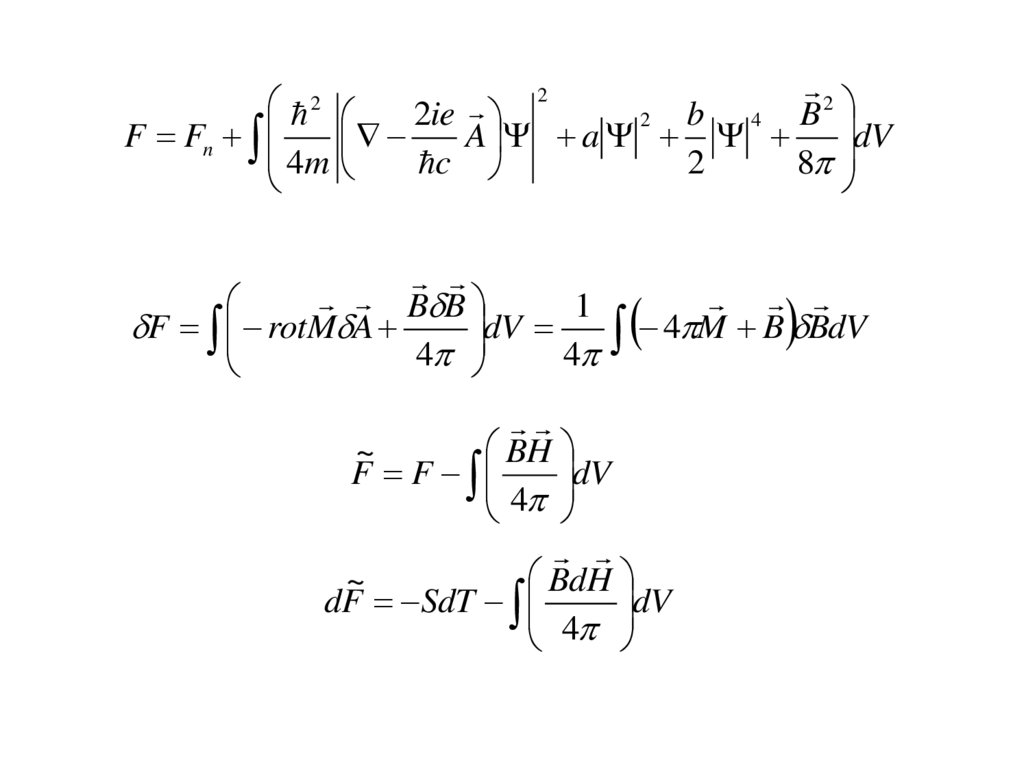








 Физика
Физика








