Похожие презентации:
Основы классической теории электропроводности металлов
1. Лекция 6
Основы классической теорииэлектропроводности
металлов
2.
2.10. Природа носителей тока в металлах.2.11.
Основные
положения
классической
электронной теории проводимости металлов
Друде – Лоренца.
2.12. Вывод законов Ома, Джоуля-Ленца и
Видемана-Франца на основе теории Друде Лоренца.
2.13.
Затруднения
классической
теории
электропроводности
металлов.
Сверхпроводимость
металлов.
Открытие
высокотемпературной сверхпроводимости.
3. 2.10. Природа носителей тока в металлах.
Для выяснения природы носителей тока в металлах был поставлен ряд опытов.Опыт Рикке (Riecke C., 1845-1915). В 1901г. Рикке осуществил опыт, в котором
он пропускал ток через стопку цилиндров с тщательно отполированными
торцами Cu-Al-Cu. Перед началом опыта образцы были взвешены с высокой
степенью точности (Δm = ±0,03 мг). Ток пропускался в течение года. За это
время через цилиндры прошел заряд q = 3,5∙106 Кл.
По окончании опыта цилиндры были вновь взвешены. Взвешивание показало, что
пропускание тока не оказало никакого влияния на вес цилиндров. При
исследовании торцевых поверхностей под микроскопом также не было
обнаружено проникновения одного металла в другой. Результаты опыта Рикке
свидетельствовали о том, что носителями тока в металлах являются не
атомы, а какие-то частицы, которые входят в состав всех металлов.
Такими частицами могли быть электроны, открытые в 1897 г. Томсоном (Thomson
J., 1856-1940) в опытах с катодными лучами. Чтобы отождествить носители
тока в металлах с электронами, необходимо было определить знак и величину
удельного
заряда носителей. Это
_
Cu
было осуществлено в
+
опыте Толмена и
Al
Стюарта (Tolman R.,
Cu
1881-1948, Stewart B.,
1828-1887).
Рис.6.1. Опыт Рикке.
4.
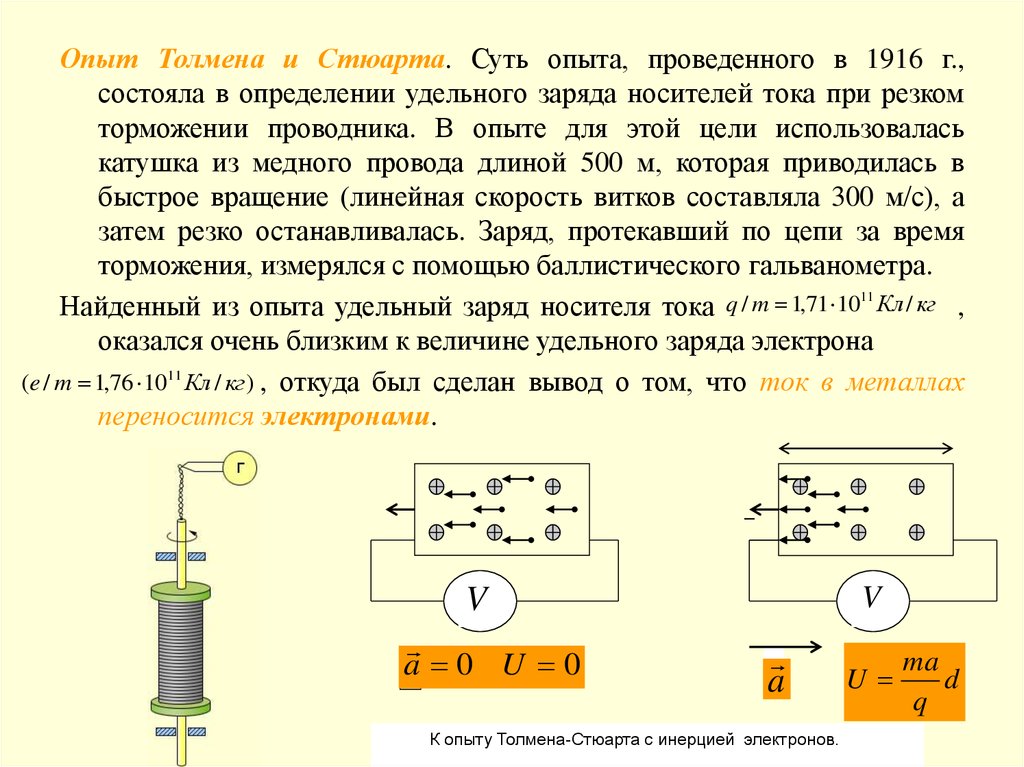
Опыт Толмена и Стюарта. Суть опыта, проведенного в 1916 г.,состояла в определении удельного заряда носителей тока при резком
торможении проводника. В опыте для этой цели использовалась
катушка из медного провода длиной 500 м, которая приводилась в
быстрое вращение (линейная скорость витков составляла 300 м/с), а
затем резко останавливалась. Заряд, протекавший по цепи за время
торможения, измерялся с помощью баллистического гальванометра.
Найденный из опыта удельный заряд носителя тока q / m 1,71 1011 Кл / кг ,
оказался очень близким к величине удельного заряда электрона
(e / m 1,76 1011 Кл / кг ) , откуда был сделан вывод о том, что ток в металлах
переносится электронами.
_
V
V
a 0 U 0
a
К опыту Толмена-Стюарта с инерцией электронов.
U
ma
d
q
5. 2.11. Основные положения классической электронной теории проводимости металлов Друде – Лоренца.
Исходя из представлений о свободных электронах как основных носителях тока в металлах,Друде (Drude P., 1863-1906) разработал классическую теорию электропроводности металлов,
которая затем была усовершенствована Лоренцем (Lorentz H., 1853-1928).
Основные положения этой теории сводятся к следующим:
1). Носителями тока в металлах являются электроны, движение которых подчиняется
законом классической механики.
2). Поведение электронов подобно поведению молекул идеального газа (электронный
газ).
3). При движении электронов в кристаллической решетке можно не учитывать
столкновения электронов друг с другом.
4). При упругом столкновении электронов с ионами электроны полностью передают
им накопленную в электрическом поле энергию.
Средняя тепловая скорость хаотического движения электронов при Т ≈ 300К составляет
8kT
8 1,38 10 23 300
10 5 м / с 100км / c
.
31
m
3,14 9,1 10
При включении электрического поля на хаотическое движение электронов накладывается
упорядоченное движение (называемое иногда «дрейфовым»), происходящее с некоторой
средней скоростью u ; возникает направленное
движение
электронов – электрический ток.
Плотность тока определяется по формуле
.
j ne u
Оценки показывают, что при максимально допустимой
плотности тока в металлах j = 107 А/м2
и концентрации носителей 1028 – 1029м-3 ,
. Таким
образом, даже при очень
u 10 3 м / с 1мм
/c
больших плотностях тока средняя скорость упорядоченного движения электронов
u .
6.
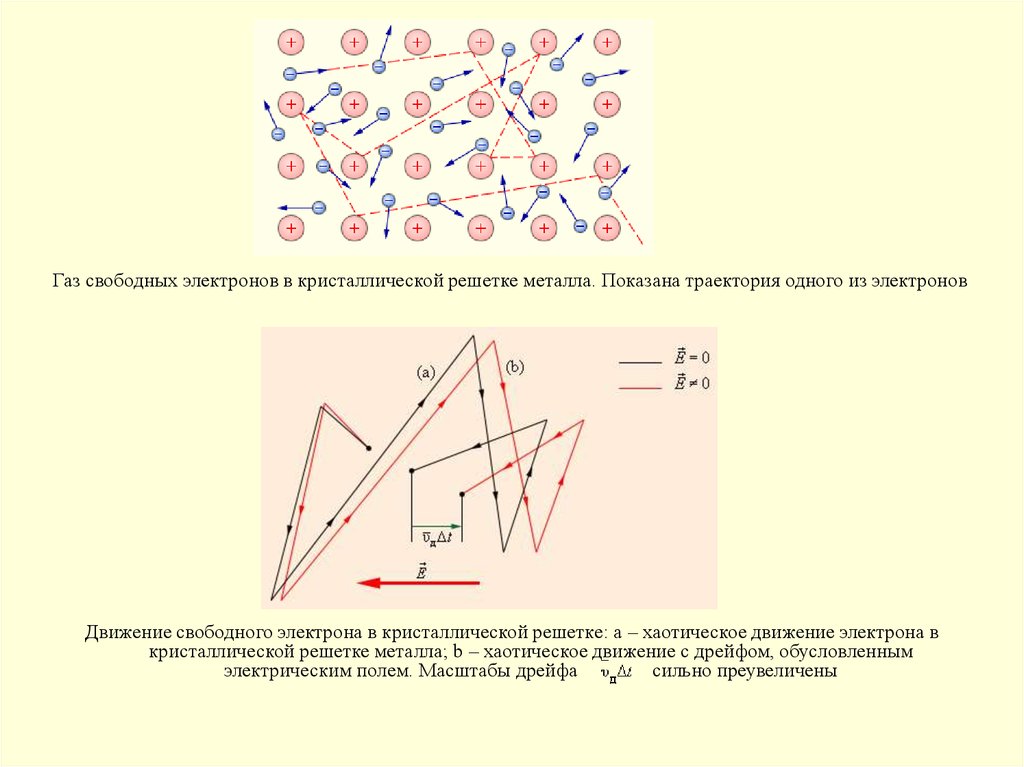
Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электроновДвижение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в
кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным
электрическим полем. Масштабы дрейфа
сильно преувеличены
7. 2.12. Вывод законов Ома, Джоуля-Ленца и Видемана-Франца на основе теории Друде-Лоренца.
Закон Ома.Ускорение, приобретаемое электроном в электрическом поле
e
На пути свободного пробега
величины
eE
a
.
m
Е
λ максимальная
скорость электрона достигнет
u max
eE
m
,
где τ - время свободного пробега: / .
Среднее значение скорости упорядоченного
движения есть:
u
eE
u
.
2
2m
Подставив это значение в формулу для плотности тока, будем иметь:
ne
j u ne
E ,
2m v
max
2
Полученная формула представляет собой закон Ома в дифференциальной форме:
ne 2
j E ,
2m
где σ – удельная электропроводность металла:
ne 2
ne 2
2m
2m
.
8.
Закон Джоуля - ЛенцаКинетическая энергия электрона, которую он имеет к моменту
соударения с ионом:
2
m 2
mumax
E кин
.
2
2
При столкновении с ионом энергия, полученная электроном в
2
электрическом поле E mumax , полностью передается иону. Число
кин
1
2
соударений одного электрона в единицу времени равно
, где λ
– длина свободного пробега электрона. Общее число столкновений
за единицу времени в единице объема равно N n
. Тогда
количество тепла, выделяющегося в единице объема проводника за
единицу времени будет:
2
2
Q уд N
mumax
ne 2
E
2
2m
.
Последнюю формулу можно представить в виде закона Джоуля-Ленца в
дифференциальной форме:
1
Q уд Е 2 E 2
,
где ρ =1/σ – удельное сопротивление металла.
9.
Закон Видемана-Франца.Из
опыта
известно,
что
металлы,
наряду
с
высокой
электропроводностью, обладают также высокой теплопроводностью.
Видеман (Wiedemann G., 1826-1899) и Франц (Franz R.,) установили в
1853 г. эмпирический закон, согласно которому отношение
коэффициента
теплопроводности
κ
к
коэффициенту
электропроводности σ для всех металлов приблизительно одинаково и
изменяется пропорционально абсолютной температуре:
.
8
2
,
3
10
Т
Рассматривая электроны как одноатомный
газ, можем на основании
кинетической
теории
газов
написать
для
коэффициента
теплопроводности электронного газа:
1
1
,
nm cv nk
3
2 при постоянном
3 k - удельная теплоемкость одноатомного
где
газа
cv
объеме.
2m
Разделив κ на σ, приходим к закону Видемана-Франца:
.
k
3 T
e и е = 1,6·10-19 Кл, найдем, что
Подставив сюда k = 1,38·10-23 Дж/К
2
,
что очень хорошо согласуется с
2,23 10 8 Т
экспериментальными
данными.
10. 2.13. Затруднения классической теории электропроводности металлов. Сверхпроводимость металлов. Открытие высокотемпературной сверхпроводи
2.13. Затруднения классической теорииэлектропроводности металлов. Сверхпроводимость
металлов. Открытие высокотемпературной
сверхпроводимости.
Несмотря на достигнутые успехи, классическая электронная теория
проводимости металлов Друде-Лоренца не получила дальнейшего
развития.
Связано это с двумя основными причинами:
1) трудностями, с которыми столкнулась эта теория при объяснении
некоторых свойств металлов;
2) созданием более совершенной квантовой теории проводимости
твердых тел, устранившей затруднения классической теории и
предсказавшей ряд новых свойств металлов.
11.
Выделим основные затруднения теории Друде-Лоренца:1. Согласно классической теории, зависимость удельного сопротивления
металлов от температуры ~ T в то время, как на опыте в широком
интервале температур вблизи Т≈300К для большинства металлов
наблюдается зависимость ρ ~ Т.
2. Хорошее количественное совпадение с законом Видемана-Франца
оказалось в известной степени случайным. В первоначальном
варианте теории Друде не учитывал распределение электронов по
скоростям. Позже, когда Лоренц учел это распределение, оказалось,
2
что отношение будет
k
2 T
,
e
что значительно хуже согласуется с экспериментом. Согласно же
2
квантовой теории,
2 k
8
T 2,45 10 Т
.
3 e
3. Теория дает неправильное значение теплоемкости металлов. С
учетом теплоемкости электронного газа С=9/2R, а на практике С=3R,
что примерно соответствует теплоемкости диэлектриков.
4. Наконец, теория оказалась полностью неспособной объяснить
открытое в 1911г. Камерлинг-Оннесом (Kamerligh-Onnes H., 18531926)
явления
сверхпроводимости
(полного
исчезновения
сопротивления) металлов при низких температурах, а также
существования остаточного сопротивления, в сильной степени
зависящего от чистоты металла.
12.
12
Тк
1-металл с
примесями
2-чистый металл
Т
Зависимость сопротивления металлов от температуры.
(Тк – температура перехода в сверхпроводящее состояние)
Интересно отметить, что в отношении
низкотемпературных сверхпроводников
(металлов) действует правило: металлы с
более высоким удельным сопротивлением
ρ имеют и более высокую критическую
температуру сверхпроводящего перехода
Ткр (см. таблицу).
.
Таблица. Свойства низкотемпературных
сверхпроводников
Металл
ρ
Тк , К
Титан
1,7
0,4
Алюминий
2,5
1,2
Ртуть
9,4
4,1
Свинец
22
7,2
13.
Феноменологическая теория низкотемпературной сверхпроводимостибыла создана в 1935г. Ф.и Г. Лондонами (London F., 1900-1954, London
H., 1907-1970), но лишь спустя почти полвека (в 1957г.) явление
сверхпроводимости получило окончательное объяснение в рамках
микроскопической (квантовой) теории, созданной Дж.Бардиным, Л.
Купером и Дж. Шриффером (Bardeen J., Cooper L., Schrieffer J.).
В 1986г. Дж. Беднорцем (Bednorz J.) и К. Мюллером (Müller K.) было
открыто явление высокотемпературной сверхпроводимости в
керамических металлоксидах (лантана, бария и др. элементов),
являющихся диэлектриками при комнатной температуре. Критическая
температура перехода в сверхпроводящее состояние для этих
материалов около 100К.
Теория высокотемпературной сверхпроводимости в настоящее время
находится в стадии разработки и пока далека от своего завершения.
Неясен даже механизм возникновения высокотемпературной
сверхпроводимости.











 Физика
Физика








