Похожие презентации:
Формулы зависимости между сторонами прямоугольного треугольника и радиусом окружности, вписанной в него и описанной около него
1.
Формулы зависимости между сторонамипрямоугольного треугольника
и радиусом окружности, вписанной в него
и описанной около него
2.
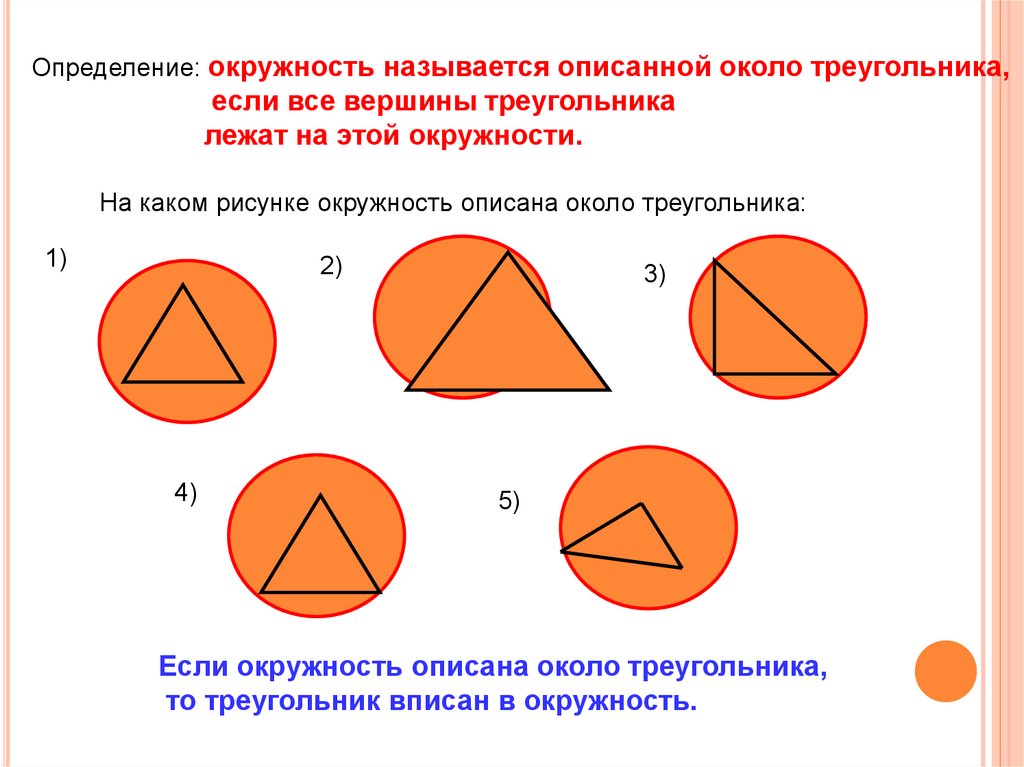
Определение: окружность называется описанной около треугольника,если все вершины треугольника
лежат на этой окружности.
На каком рисунке окружность описана около треугольника:
1)
2)
4)
3)
5)
Если окружность описана около треугольника,
то треугольник вписан в окружность.
3.
Определение: окружность называется вписанной в треугольник,если все стороны треугольника касаются окружности.
На каком рисунке окружность вписана в треугольник:
1)
4)
3)
2)
5)
Если окружность вписана в треугольник,
то треугольник описан около окружности.
4.
В прямоугольном треугольнике центр описаннойокружности совпадает с серединой гипотенузы
(гипотенуза является диаметром)
Радиус вписанной окружности находится по формуле:
r=
, где а и b – катеты, с – гипотенуза.
R = d/2
О
5. Формула для прямоугольного треугольника
ra b c
2
Элементы формулы:
а - катет треугольника;
b - катет треугольника;
с - гипотенуза треугольника;
r – радиус окружности,
вписанной в прямоугольный
треугольник
6.
a b cr
; a, b - катеты, с - гипотенуза
2
А
Доказательство:
b
М
К
С
c
Т. к. окружность (О;r) вписана
в треугольник АВС, у которого угол С- прямой,
то АС, ВС, АВ – касательные и
r Оr
r
Е
a
В
СКОЕ – квадрат, значит, СК = СЕ = r
По свойству касательных: ВЕ = ВМ = а - r
АК = АМ = b - r
AB = AM + BM
c=b–r+a-r
2r = a + b - c
r = ½ (a + b – c)
7. Формула для прямоугольного треугольника
rЗадача № 1
Катеты прямоугольного
треугольника равны 6см и 8см.
Найти радиус окружности,
вписанной в этот треугольник.
a b c
2
1.
Решение.
ВС = 6см, АС = 8см, тогда
найдем гипотенузу АВ по
теореме Пифагора:
ÀÂ 6 2 82 100 10,
2.
АВ = 10 см.
r = OK = ON = OM,
6 8 10 4
r
2,
2
2
r 2 ñì .
Ответ. 2 см.
8.
Формула для прямоугольного треугольникаГипотенуза прямоугольного треугольника равна 12. Найдите
радиус описанной окружности этого треугольника.
Решение.
Вписанный угол, опирающийся на
диаметр окружности, является прямым,
значит, гипотенуза является диаметром и
R = 12/2=6.
Ответ: 6.
9. Групповая работа
Задачи на закреплениеЗадача № 1
В прямоугольном треугольнике
один из катетов равен 3см, а
другой на 1см больше. Найти
радиус окружности, вписанной в
этот треугольник
Ответ. 1 см.
Задача № 2
Катет равнобедренного
прямоугольного треугольника
равен 6 см. Найти радиус
окружности, вписанной в этот
треугольник.
Ответ. 6 3 2 ñì .
Задача № 3
В прямоугольном треугольнике
один из катетов равен 12 см, а
гипотенуза равна 13 см. Найти
радиус окружности, вписанной в
этот треугольник.
Ответ. 2 см.
Задача № 4
Гипотенуза равнобедренного
прямоугольного треугольника
равна 4 см. Найти радиус
окружности, вписанной в этот
треугольник.
Ответ. 2 2 2 ñì .
10.
Тест1.
Центр окружности, вписанной в треугольник, является точкой пересечения:
А) серединных перпендикуляров к сторонам треугольника. В) биссектрис углов
треугольника. С) медиан треугольника. D) Высот треугольника.
E) Одной высоты и одной медианы.
2. Катеты прямоугольного треугольника равны 30 см и 40 см. Найдите радиус описанной
окружности.
А) 35 см.
В) 50 см.
С) 40 см.
D) 60 см.
E) 25 см.
3. Центром вписанной в треугольник окружности является:
А) точка пересечения биссектрис углов треугольника. В) точка пересечения
перпендикуляров. С) точка пересечения высот треугольника.
D) Точка пересечения медиан треугольника. E) Точка пересечения любых прямых,
пересекающих стороны треугольника.
4. Найдите радиус окружности, описанной около прямоугольного треугольника, если его
гипотенуза равна 10 см.
А) 5 см.
В) см.
С) – 5 см.
D) 5 см.
E) – 5 см.
5. Катеты прямоугольного треугольника равны 5 и 12. Чему равен радиус вписанной
окружности.
А) 2.
В) 4.
С) 3.
D) 2, 5.
E) 1
11.
Ответы1. В
2. Е
3. В
4. Д
5. А
12.
Домашнее задание:1. Выучить формулы и их вывод
2. Решить задачу:
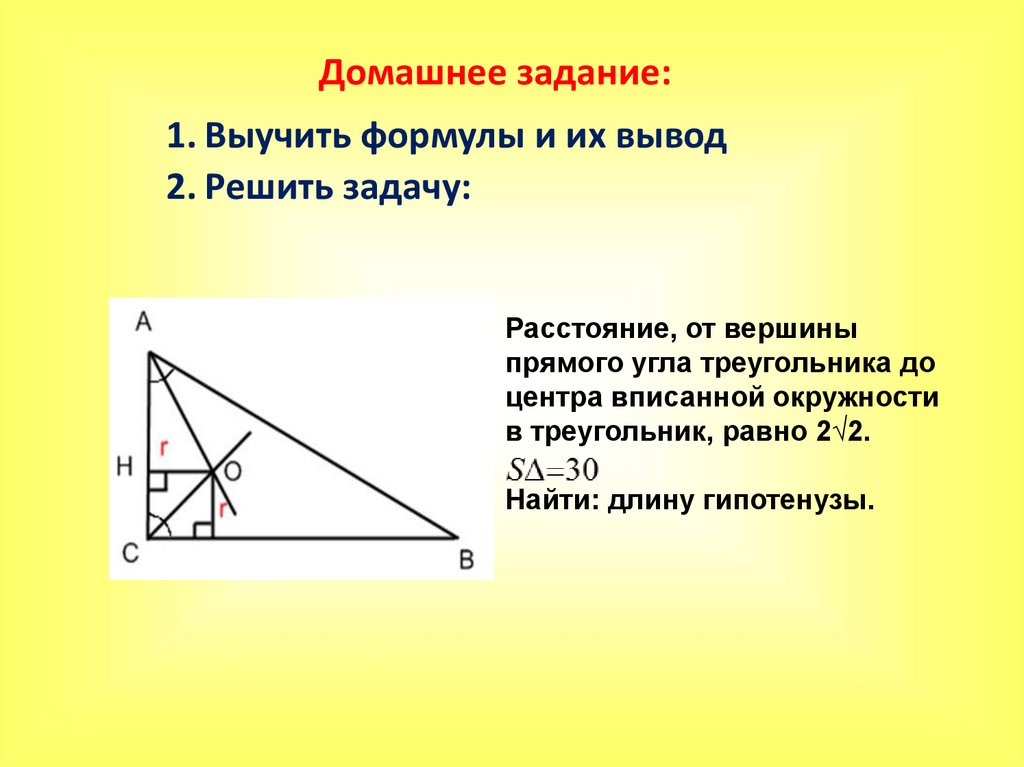
Расстояние, от вершины
прямого угла треугольника до
центра вписанной окружности
в треугольник, равно 2√2.
Найти: длину гипотенузы.











 Математика
Математика








