Похожие презентации:
Понятие о динамических нагрузках. Силы инерции при расчете на прочность
1.
Понятие о динамической нагрузке – Динамической нагрузкой является такая нагрузка, которая быстро меняет свое значение и/илиместо приложения. В результате действия динамической нагрузки возникают колебания системы (при наличии положения равновесия и
достаточных возвращающих сил ). До сих пор предполагалось, что увеличение нагрузки, например, в предыдущем разделе, происходит
медленно (постепенно) и в каждый момент времени существует точное равновесие между внешними силами и внутренними силами
(упругости). При резком изменении нагрузки материальным точкам системы сообщается некоторое ускорение и система выводится из
состояния равновесия и далее, в общем случае, точки системы движутся неравномерно по некоторым траекториям. При этом упругие связи
между ними испытывают динамические воздействия (меняющиеся во времени), возникающие внутренние силы, напряжения и деформации
могут превышать в несколько раз расчетные значения, определенные при статическом действии нагрузки.
Согласно принципу Даламбера движущуюся неравномерно (с ускорениями) систему можно рассматривать как систему, находящуюся в
равновесии, если к заданным силам добавить соответствующие силы инерции. Если это сделано, то при расчете используются известные
уравнения равновесия и другие соотношения, полученные из них, однако такой расчет (с учетом сил инерции) называют динамическим расчетом,
поскольку получаемые результаты содержат динамические составляющие усилий, зависящие от движения точек системы (ускорений) и, значит,
от параметров действующей динамической нагрузки.
S
Динамический коэффициент – есть величина, сопоставляющее динамическое значение некоторого фактора
kд д .
(усилия, напряжения, перемещения) с соответствующим статическим значением этого фактора, в виде отношения:
S ст
N
I
Пример 1: Кабина лифта весом G
поднимается тросом с ускорением a.
Определить усилие в тросе.
Определяем усилие в тросе: N G G
I 1. Проводим сечение I - I.
2. Выбираем объект (кабина лифта, нижняя часть троса).
a
3. Заменяем действие отброшенной части усилием N.
G
Ф
4. Добавляем к действующим силам силу инерции: ma .
5. Составляем уравнение равновесия: Yi 0;
N G 0.
Таким образом, динамическое значение усилия определяется через
статическое значение посредством динамического коэффициента как
ay
G
a y G 1 .
g
g
Получено динамическое значения усилия, зависящее от
величины ускорения подъема кабины. При отсутствии
ускорения (ay = 0, кабина находится в статическом
равновесии) усилие (статическое) в тросе равно весу
кабины: Nст = G.
ay
Динамический коэффициент
G 1
ay
g
Nд
равен:
kд
N ст
G
1
g
.
N д k д N ст или в общем случае: S д k д S .
Ударное действие нагрузки – При падении груза на упругую конструкцию в момент контакта между соударяемыми телами развиваются
силы взаимодействия, характеризуемые быстрым ростом их величины за очень малый отрезок времени и последующим быстрым спадом. Закон
изменения этих сил установить чрезвычайно сложно, поэтому такие динамические задачи решаются с помощью теорем динамики, которые
позволяют связать исходное и конечное состояние системы без детального рассмотрения быстро протекающих процессов между этими
состояниями.
Основной гипотезой при решении динамических задач для упругих систем является допущение, что связь между усилиями и деформациями
сохраняется при динамическом действии нагрузки такой же, как и при статическом ее действии, т.е.
F , где c – жесткость
F и
ст ст упругой связи.
д
8
д
c
c
2.
Пример 2. Удар падающего груза на упругую конструкцию. Основное назначение введенного динамического коэффициента состоит вприведении динамической задачи к статической, как это было сделано в примере 1. Здесь покажем процедуру определения динамического
коэффициента для достаточно простой, но практически важной упругой системы – жесткая платформа на упругих опорах (пружинах).
Допущения: 1. Масса упругих связей не учитывается (инерционные силы не возникают, волны упругих деформаций не возникают).
2. Соударение считаем абсолютно неупругим (нет отскока, после удара обе массы движутся совместно с одинаковой скоростью).
3. Время удара (от момента касания до момента совместного движения) равно нулю.
4. Удар считаем центральным, движение платформы поступательным (в этом случае массу платформы m можно считать точечной массой, а
пружины заменить одной пружиной с эквивалентной жесткостью c, равной сумме жесткостей пружин).
1. Определим скорость подлета падающей массы, используя теорему об изменении кинетической энергии:
M
G
m
0
h 1
1’
G1
T1 T0 A01
T0 0,
T1
Mv12
, A01 Gh Mgh.
2
v1 2 gh
2. Определим скорость движения системы сразу после удара, используя теорему об изменении количества движения:
t 1
Q1' Q1 (G G1 R)dt 0
Считая время
удара t = 0:
R
0
c Дальнейшее движение системы (M + m) будет происходить как
Q1' Q1 ,
v1
Mv1 (M m)v1 ,
Mv1
( M m)
движение упругой системы с одной степенью свободы с начальными
условиями y0 = 0 и v0 = v’1 - колебание относительно положения
равновесия, y = - ст, с амплитудой a, зависящей от скорости v0
и круговой частоты k . Здесь и далее ст - статическая деформация
от веса груза, поскольку начало координат принято совпадающим
с положением платформы до падения груза, т.е. пружина уже
имела статическую деформацию от веса платформы.
Наибольшее усилие в пружине Nд = Rд возникает в положении
максимального сжатия. В этот момент скорость движения падает до нуля
и кинетическая энергия системы обращается в ноль.
N
Связь между деформацией и усилием N в общем виде:
.
Статическая деформация (при равновесии):
Максимальная (динамическая) деформация:
ст
д
a
c
N ст Q
ст
.
c
c
Nд
д
.
c
Из последних соотношений видно, что все факторы при ударе (усилия, деформации) пропорциональны этим факторам,
определенным при статическом действии нагрузки (равновесии). Коэффициентом пропорциональности является динамический
коэффициент, который и следует определить.
9
3.
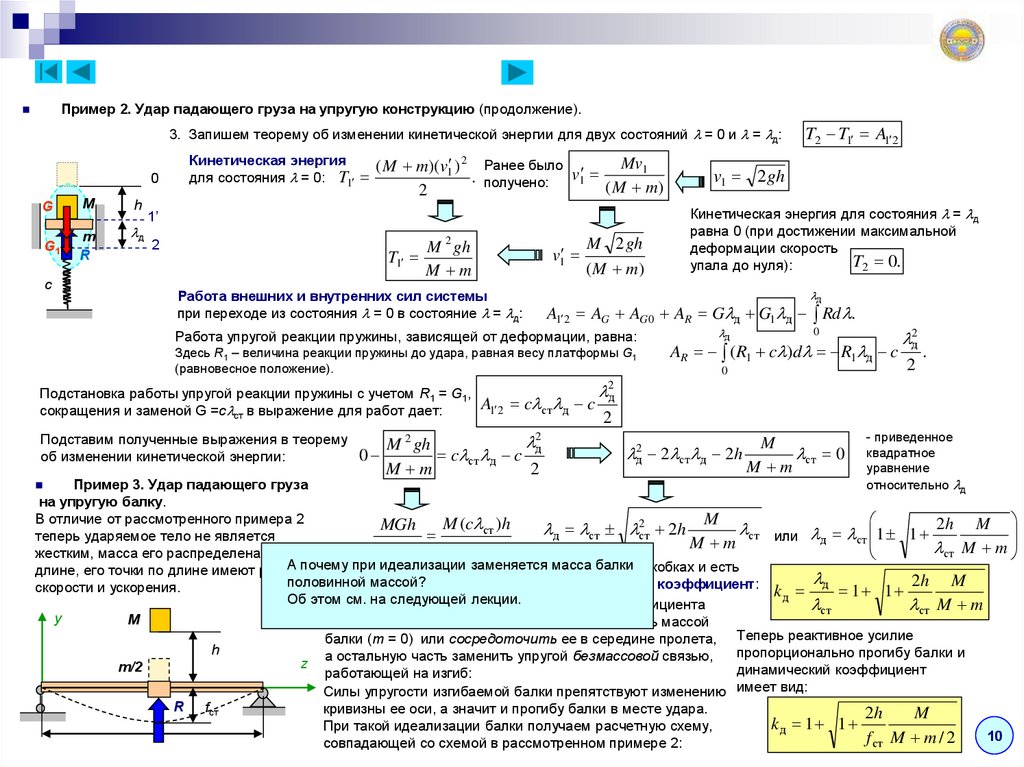
Пример 2. Удар падающего груза на упругую конструкцию (продолжение).3. Запишем теорему об изменении кинетической энергии для двух состояний = 0 и = д:
0
G
G1
c
M
m
R
h
д
Кинетическая энергия
( M m)(v1 ) 2 Ранее было v
для состояния = 0: T1
. получено:
1
2
Mv1
( M m)
1’
2
T1
M 2 gh
M m
v1
M 2 gh
( M m)
и
T2 T1 A1 2
v1 2 gh
Кинетическая энергия для состояния = д
равна 0 (при достижении максимальной
деформации скорость
T2 0.
упала до нуля):
д
Работа внешних и внутренних сил системы
при переходе из состояния = 0 в состояние = д:
A1 2 AG AG 0 AR G д G1 д Rd .
Работа упругой реакции пружины, зависящей от деформации, равна:
Здесь R1 – величина реакции пружины до удара, равная весу платформы G1
(равновесное положение).
д
0
AR ( R1 c )d R1 д c
0
2д
2
.
д
Подстановка работы упругой реакции пружины с учетом R1 = G1,
A
c
c
1
2
ст
д
сокращения и заменой G =с ст в выражение для работ дает:
2
2
Подставим полученные выражения в теорему
об изменении кинетической энергии:
0
2
2д
M gh
c ст д c
M m
2
2д 2 ст д 2h
M
ст 0
M m
- приведенное
квадратное
уравнение
относительно д
Пример 3. Удар падающего груза
на упругую балку.
В отличие от рассмотренного примера 2
M
M (c ст )h
MGh
д ст 2ст 2h
ст или д ст 1 1 2h M
теперь ударяемое тело не является
M m
ст M m
M m
M m
жестким, масса его распределена по
А почему при идеализации заменяется Выражение
масса балкив скобках и есть
длине, его точки по длине имеют разные
д
2h M
половинной
массой?
динамический
коэффициент:
скорости и ускорения.
k
1
1
д
Об этом
см. на следующей
Полученную
формулу лекции.
для динамического коэффициента
ст
ст M m
y
M
можно применить к этой задаче, если пренебречь массой
балки (m = 0) или сосредоточить ее в середине пролета, Теперь реактивное усилие
h
пропорционально прогибу балки и
а остальную часть заменить упругой безмассовой связью,
z
m/2
динамический коэффициент
работающей на изгиб:
Силы упругости изгибаемой балки препятствуют изменению имеет вид:
R fст
кривизны ее оси, а значит и прогибу балки в месте удара.
2h
M
l
kд 1 1
При такой идеализации балки получаем расчетную схему,
10
f ст M m / 2
совпадающей со схемой в рассмотренном примере 2:
4.
Динамический коэффициент при ударе – Примеры 2 и 3 показывают путь решения задач при ударе для упругих конструкций.Полученная формула для динамического коэффициента может использоваться в различных
д
v2
других практических случаях (продольный, поперечный удар при изгибе, удар с кручением)
kд
1 1
и в более общем случае имеет вид:
g
ст
ст
Здесь использована скорость падающего груза вместо высоты падения. Это позволяет отказаться от стереотипа падающего груза и
решать другие интересные задачи, в которых скорость подлета ударяющей массы вычисляется иначе.
Коэффициент учитывает соотношение ударяемой и ударяющих масс (при кручении соотношение моментов инерции масс).
Для каждого из частных случаев используется соответствующие характеристики деформации (продольное перемещение, прогиб, угол
закручивания), определенные при статическом действии динамической нагрузки.
2T
Замечания: 1. Еще более общий вид формулы для динамического коэффициента можно получить
v2
,
2
T
M
с использованием кинетической энергии ударяющей массы T = Mv /2 и потенциальной
kд 1 1
2
U
энергии деформации при статическом приложении нагрузки Uст = G ст/2 = Mg ст/2:
ст
U ст
g ст
Таким образом, теперь формула не содержит особенностей, связанных
M
с характером ударного воздействия и видом деформации.
2. Если высота падения равна нулю (скорость или кинетическая энергия ударной массы равна нулю), то динамический коэффициент равен 2.
Это, так называемый, мгновенный удар (мгновенное приложение нагрузки). Это явление может произойти, например, при выбивании кувалдой
стойки опалубки бетонного элемента перекрытия (собственный вес и/или полезная нагрузка мгновенно передается на этот элемент).
3. Во всех приведенных видах формулы динамического учитывается вклад силы тяжести при исчислении работы или энергии деформации
(вертикальный удар). В случае горизонтального удара формула для динамического коэффициента будет выглядеть иначе:
M
v
v1
m
R
Mv1
( M m)v12
; T1
; T2 0.
( M m)
2
д
д
0
0
A1 2 AR Rd . c d c
2д
2
T2 T1 A1 2
2
4. При рассмотрении динамического удара в случае резкого торможения быстро вращающегося
маховика динамический коэффициент теряет смысл, поскольку нельзя сопоставить соответствующее
статическое действие. Тем не менее динамическое усилие возникает (динамический
д
крутящий момент) и его можно найти с использованием теоремы об изменении
k
д
кинетической энергии или закона сохранения механической энергии:
T0 U д ,
I z 02
T0
;
2
U ст
M д,2 кр l
2GI
M 2v 2
0
c д
2( M m)
2
ст
M (c ст )v 2
MGv 2
2 g ( M m) 2 g ( M m)
v2
g ст
2д v 2
M
ст
g ( M m)
.
Здесь Iz – осевой момент инерции массы маховика, I -полярный момент инерции поперечного сечения вала.
11
5.
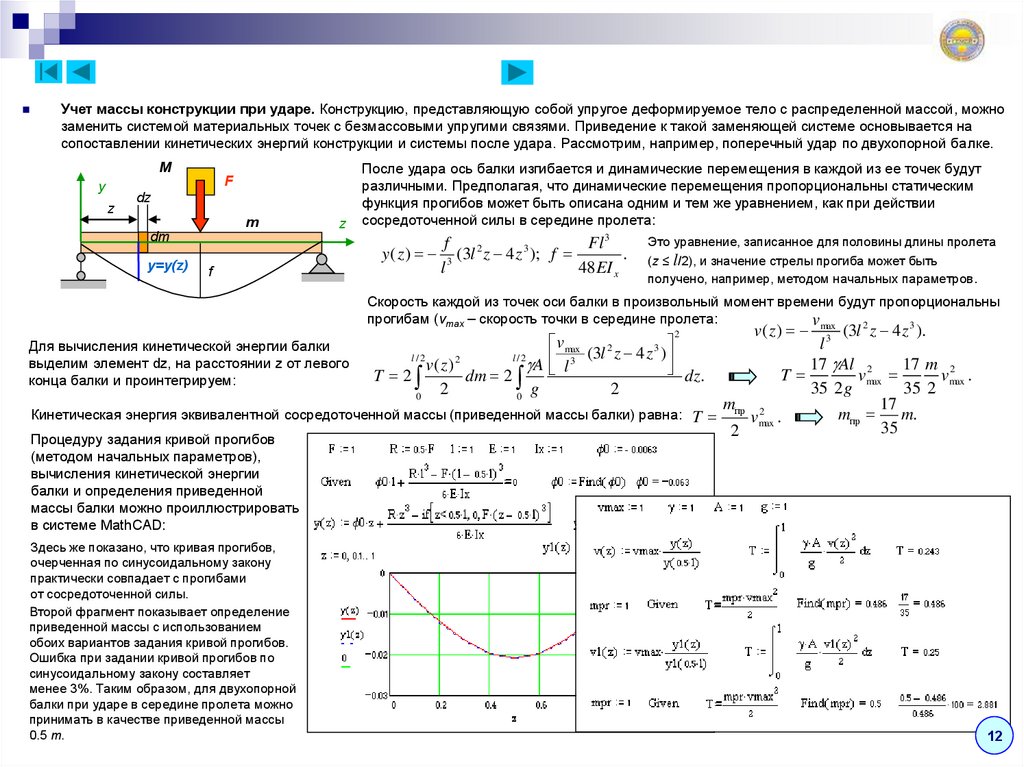
Учет массы конструкции при ударе. Конструкцию, представляющую собой упругое деформируемое тело с распределенной массой, можнозаменить системой материальных точек с безмассовыми упругими связями. Приведение к такой заменяющей системе основывается на
сопоставлении кинетических энергий конструкции и системы после удара. Рассмотрим, например, поперечный удар по двухопорной балке.
M
F
y
z
dz
m
z
dm
y=y(z)
f
После удара ось балки изгибается и динамические перемещения в каждой из ее точек будут
различными. Предполагая, что динамические перемещения пропорциональны статическим
функция прогибов может быть описана одним и тем же уравнением, как при действии
сосредоточенной силы в середине пролета:
f
Fl 3
y ( z ) 3 (3l 2 z 4 z 3 ); f
.
l
48EI x
Это уравнение, записанное для половины длины пролета
(z ≤ l/2), и значение стрелы прогиба может быть
получено, например, методом начальных параметров .
Скорость каждой из точек оси балки в произвольный момент времени будут пропорциональны
прогибам (vmax – скорость точки в середине пролета:
vmax
2
3
(3l z 4 z ).
l3
17 Al 2
17 m 2
T
vmax
vmax .
35 2 g
35 2
17
m 2
Кинетическая энергия эквивалентной сосредоточенной массы (приведенной массы балки) равна: T пр vmax
mпр m.
.
35
2
Для вычисления кинетической энергии балки
выделим элемент dz, на расстоянии z от левого
конца балки и проинтегрируем:
2
vmax
(3l 2 z 4 z 3 )
l/2
l/2
2
3
v( z )
A l
dz.
T 2
dm 2
2
g
2
0
0
v( z )
Процедуру задания кривой прогибов
(методом начальных параметров),
вычисления кинетической энергии
балки и определения приведенной
массы балки можно проиллюстрировать
в системе MathCAD:
Здесь же показано, что кривая прогибов,
очерченная по синусоидальному закону
практически совпадает с прогибами
от сосредоточенной силы.
Второй фрагмент показывает определение
приведенной массы с использованием
обоих вариантов задания кривой прогибов.
Ошибка при задании кривой прогибов по
синусоидальному закону составляет
менее 3%. Таким образом, для двухопорной
балки при ударе в середине пролета можно
принимать в качестве приведенной массы
0.5 m.
12



 Механика
Механика








