Похожие презентации:
Пирамида по материалам открытого банка задач ЕГЭ по математике. Решение заданий №3
1. Решение заданий №3 Пирамида по материалам открытого банка задач ЕГЭ по математике
2.
№1Стороны основания правильной четырехугольной пирамиды
равны 100, боковые ребра равны 130. Найдите площадь боковой
поверхности этой пирамиды.
Решение.
В правильной пирамиде боковые
грани равнобедренные треугольники .
SH высота и медиана одного из них.
В п / у SHC по т. Пифагора
S
130
h
С
50
Н
D
O
A
100
B
SH 2 SC 2 HC 2
SH 2 130 2 50 2 120 2
SH 120
1
S бок. Pосн. SН
2
Pосн. 4 АВ 4 100 400
1
S бок. 400 120 24000.
2
Ответ: 24000.
3.
№2Стороны основания правильной шестиугольной пирамиды равны
100, боковые ребра равны 130. Найдите площадь боковой
поверхности этой пирамиды.
Решение.
S
В правильной пирамиде боковые
грани равнобедренные треугольники .
SH высота и медиана одного из них.
В п / у SHC по т. Пифагора
130
SH 2 SC 2 HC 2
D
SH 2 130 2 50 2 120 2
SH 120
1
S бок. Pосн. SН
2
Pосн. 6 АВ 6 100 600
M
E
F
C
50
Н
O
A
100
B
1
S бок. 600 120 36000.
2
Ответ: 36000.
4.
№3Во сколько раз увеличится объём правильного тетраэдра, если все
его ребра увеличить в десять раз?
Решение.
S
Объемы подобных тел относятся
как куб коэффицент а подобия
V2
k 3 103 1000.
V1
a
h
А
С
O
a
В
Ответ: 1000.
5.
№4Основанием пирамиды является прямоугольник со сторонами 30 и
40. Ее объём равен 16000. Найдите высоту этой пирамиды.
Решение.
1
Vпир. S осн. h
3
S осн. АВ BC 40 30 1200
S
3 16000
h
40.
S осн.
1200
3Vпир.
h
С
D
30
O
A
40
B
Ответ: 40.
6.
№5Найдите объём правильной треугольной пирамиды, стороны
основания которой равны 10, а высота равна 10√3.
Решение.
S
1
Vпир. S осн. h
3
Площадь правильного треугольника
10 3
А
С
O
H
АВ 2 3 10 2 3
S осн.
25 3
4
4
1
1
Vпир. S осн. h 25 3 10 3 250.
3
3
10
В
Ответ: 250.
7.
№6Найдите высоту правильной треугольной пирамиды, стороны
основания которой равны 20, а объём равен 1000√3.
Решение.
S
1
Vпир. S осн. h
3
Площадь правильного треугольника
h
А
С
O
H
АВ 2 3 20 2 3
S осн.
100 3
4
4
3Vпир. 3 1000 3
h
30.
S осн.
100 3
20
В
Ответ: 30.
8.
№7Во сколько раз увеличится объём пирамиды, если ее высоту
увеличить в пятнадцать раз?
S
a
h
А
O
a
Решение.
При увеличении высоты в 15 раз
объем пирамиды увеличится
также в 15 раз
1
Vпир.1 S осн. h
3
С Vпир.2 1 S осн. 15h 15 Vпир.1
3
В
Ответ: 15.
9.
№8В правильной четырехугольной пирамиде высота равна 60,
боковое ребро равно 100. Найдите ее объём.
Решение.
В п / у ASО по т. Пифагора
S
АО 2 SА2 SO 2
AO 2 100 2 60 2 80 2
AO 80
100
AB 80 2
60
С
D
O
A
B
2
S осн. АВ 80 2 12800
2
1
Vпир. S осн. h
3
1
Vпир. 12800 60 256000.
3
Ответ: 256000.
10.
№9Основанием пирамиды служит прямоугольник, одна боковая
грань перпендикулярна плоскости основания, а три другие
боковые грани наклонены к плоскости основания под углом 60°.
Высота пирамиды равна 9. Найдите объём пирамиды.
Решение.
S
9
D
60°
Р
Н
A
B
ASD р / c , т.к . SAH SDH 60
( как линейные углы двугранных углов
при сторонах основания АВ и CD )
SH
9
В п / у SHP HP
3 3
tg 60
3
С AD 2SH 2 9 6 3
3
3
как сторона р / с ASD
S осн . AB AD HP AD 3 3 6 3 54
1
1
Vпир. S осн . h 54 9 162.
3
3
Ответ: 162.
11.
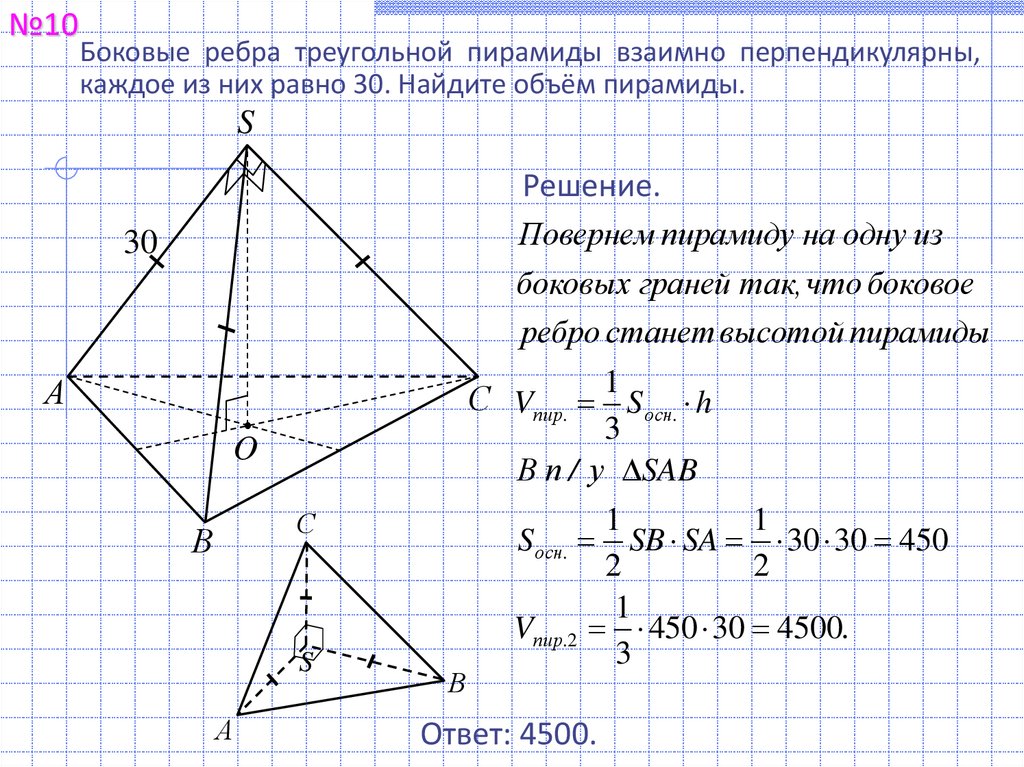
№10Боковые ребра треугольной пирамиды взаимно перпендикулярны,
каждое из них равно 30. Найдите объём пирамиды.
S
30
А
O
С
В
S
А
В
Решение.
Повернем пирамиду на одну из
боковых граней так, что боковое
ребро станет высотой пирамиды
1
С Vпир. S осн. h
3
В п / у SAB
1
1
S осн. SB SA 30 30 450
2
2
1
Vпир.2 450 30 4500.
3
Ответ: 4500.
12.
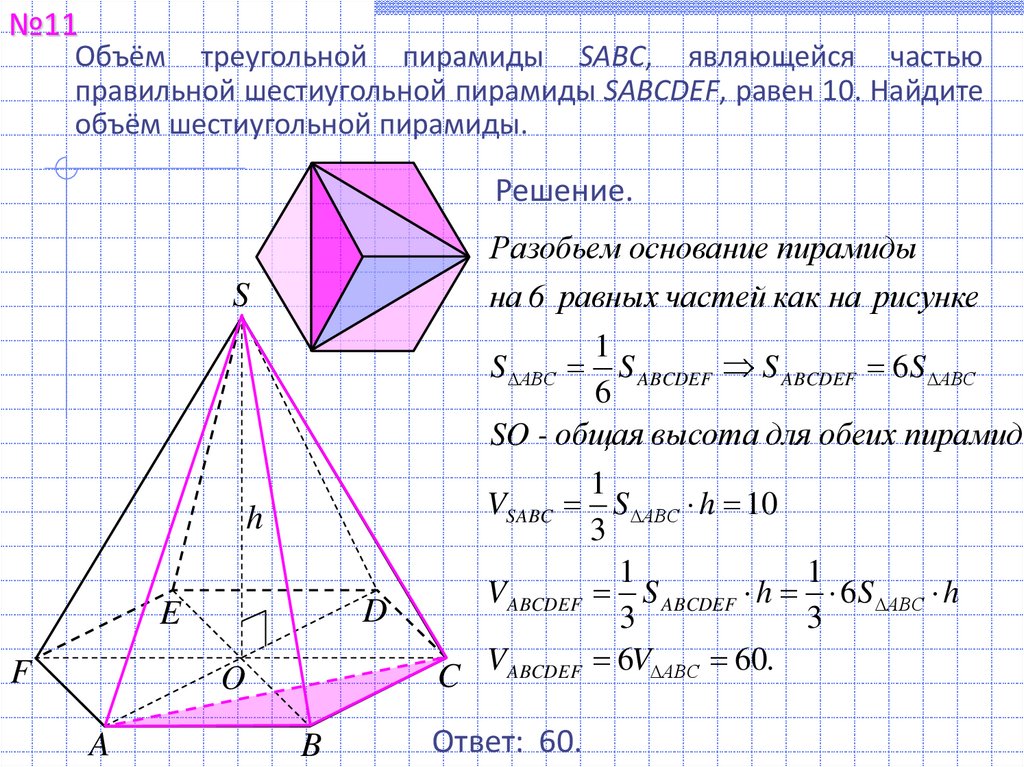
№11Объём треугольной пирамиды SABC, являющейся частью
правильной шестиугольной пирамиды SABCDEF, равен 10. Найдите
объём шестиугольной пирамиды.
Решение.
S
h
D
E
F
C
O
A
B
Разобьем основание пирамиды
на 6 равных частей как на рисунке
1
S АВС S ABCDEF S ABCDEF 6 S АВС
6
SO - общая высота для обеих пирамид
1
VSABC S АВС h 10
3
1
1
VABCDEF S ABCDEF h 6 S АВС h
3
3
VABCDEF 6V АВС 60.
Ответ: 60.
13.
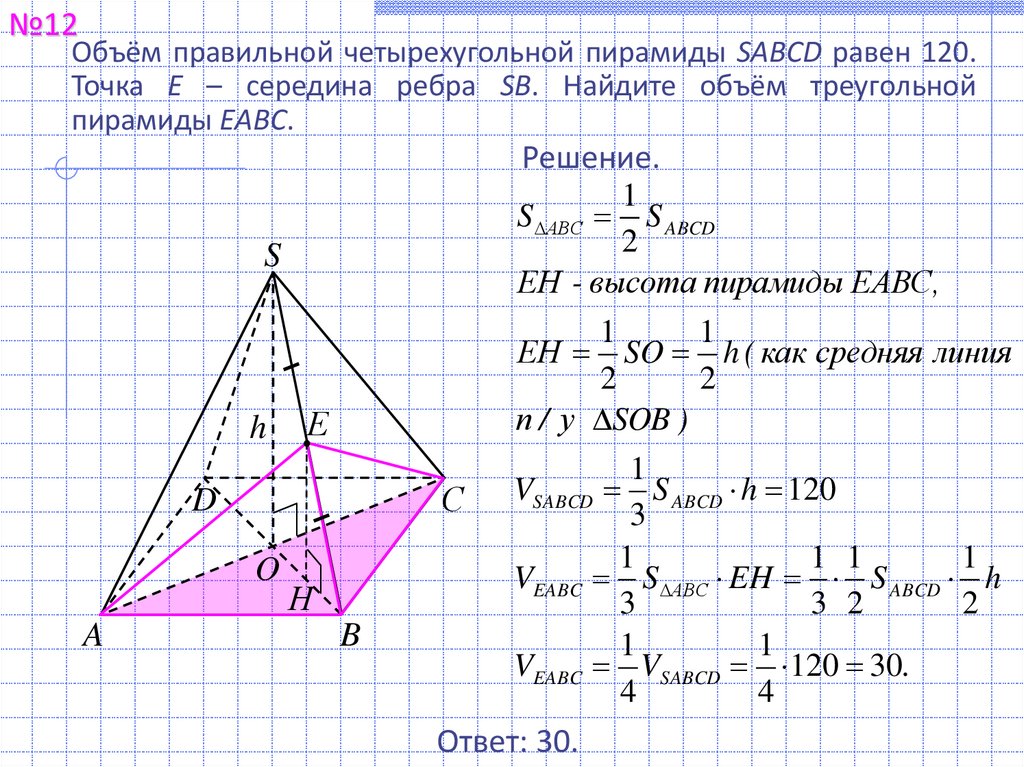
№12Объём правильной четырехугольной пирамиды SABCD равен 120.
Точка E – середина ребра SB. Найдите объём треугольной
пирамиды EABC.
S
h
Е
D
O
A
Н
B
Решение.
1
S АВС S ABCD
2
ЕН - высота пирамиды ЕАВС,
1
1
ЕН SO h ( как средняя линия
2
2
п / у SOB )
1
V
S ABCD h 120
SABCD
С
3
1
1 1
1
VEABC S АВС EH S ABCD h
3
3 2
2
1
1
VEABC VSABCD 120 30.
4
4
Ответ: 30.
14.
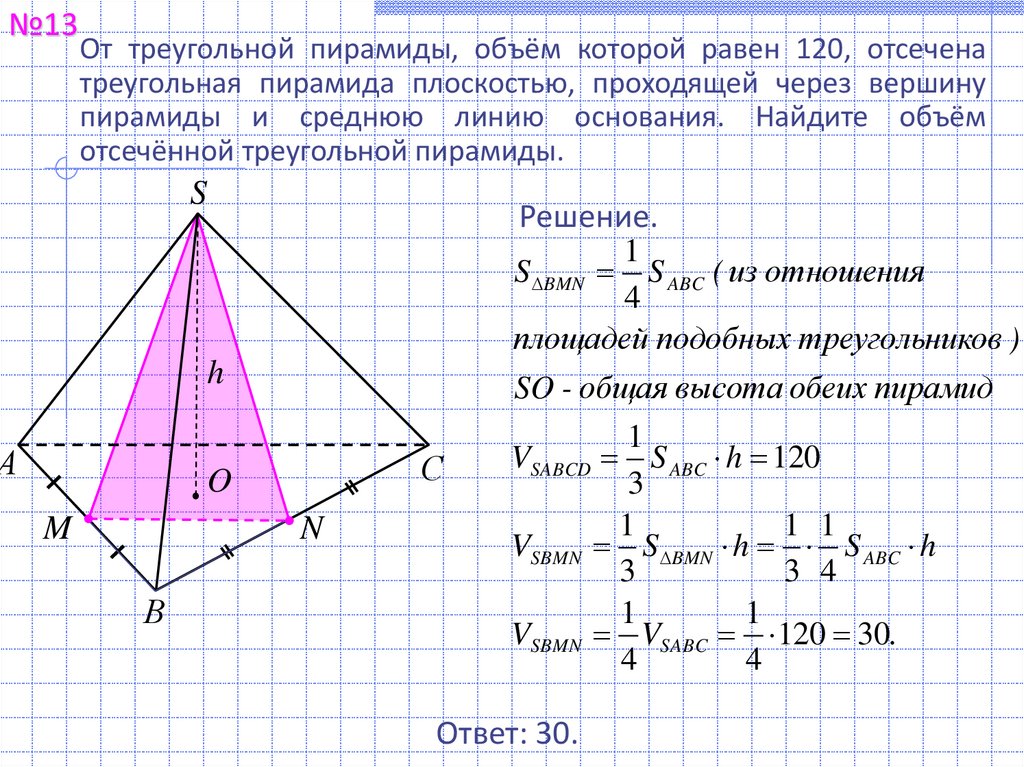
№13От треугольной пирамиды, объём которой равен 120, отсечена
треугольная пирамида плоскостью, проходящей через вершину
пирамиды и среднюю линию основания. Найдите объём
отсечённой треугольной пирамиды.
S
h
А
С
O
M
N
В
Решение.
1
S BMN S ABC ( из отношения
4
площадей подобных треугольников )
SO - общая высота обеих пирамид
1
VSABCD S ABC h 120
3
1
1 1
VSBMN S BMN h S ABC h
3
3 4
1
1
VSBMN VSABC 120 30.
4
4
Ответ: 30.
15.
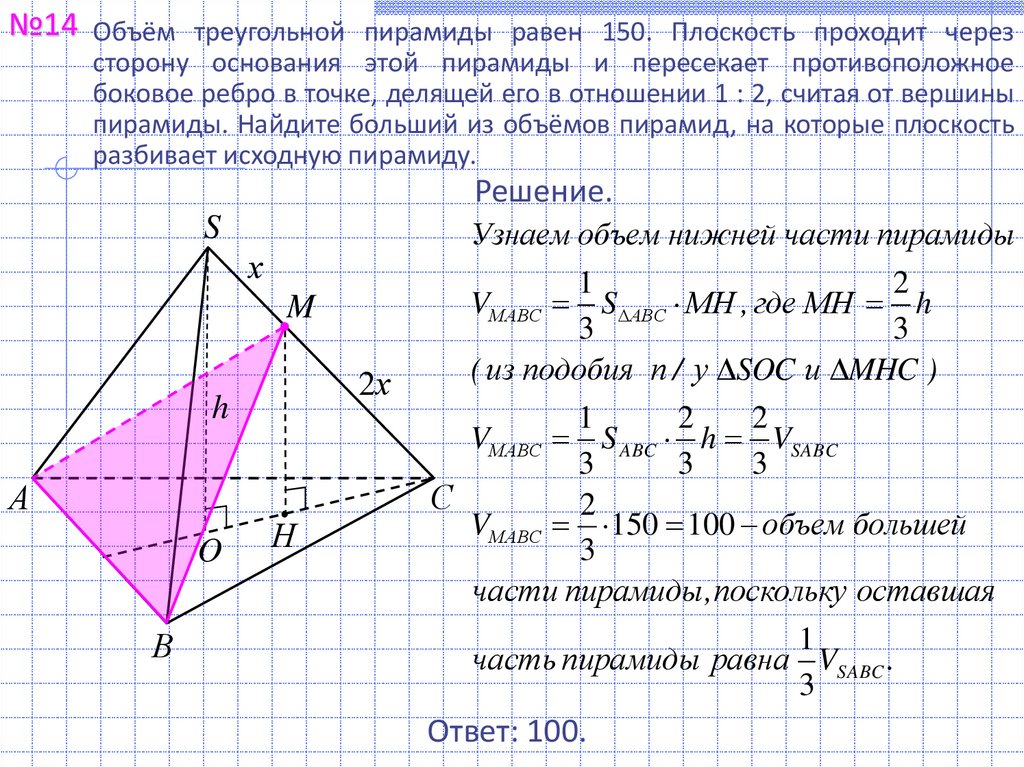
№14 Объём треугольной пирамиды равен 150. Плоскость проходит черезсторону основания этой пирамиды и пересекает противоположное
боковое ребро в точке, делящей его в отношении 1 : 2, считая от вершины
пирамиды. Найдите больший из объёмов пирамид, на которые плоскость
разбивает исходную пирамиду.
Решение.
S
х
M
2х
h
А
O
В
Н
Узнаем объем нижней части пирамиды
1
2
VМABC S АВС МH , где МН h
3
3
( из подобия п / у SOC и MHC )
1
2
2
VМABC S ABC h VSABC
3
3
3
С
2
VМABC 150 100 объем большей
3
части пирамиды , поскольку оставшая
1
часть пирамиды равна VSABC .
3
Ответ: 100.
16.
№15Во сколько раз увеличится площадь поверхности правильного
тетраэдра, если все его рёбра увеличить в десять раз?
Решение.
S
Площади подобных тел относятся
как квадрат коэффициента подобия
S2
k 2 10 2 100 .
S1
a
h
А
С
O
a
В
Ответ: 100.
17.
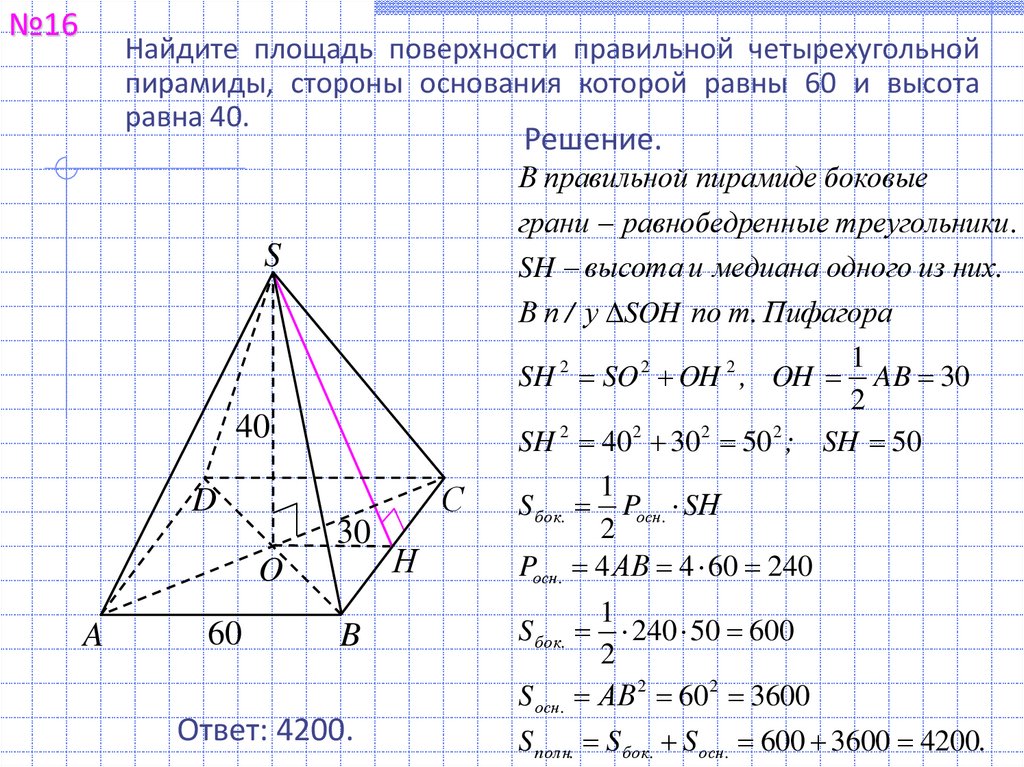
№16Найдите площадь поверхности правильной четырехугольной
пирамиды, стороны основания которой равны 60 и высота
равна 40.
Решение.
S
40
С
D
30
O
A
60
B
Ответ: 4200.
Н
В правильной пирамиде боковые
грани равнобедренные треугольники .
SH высота и медиана одного из них.
В п / у SOH по т. Пифагора
1
SH 2 SO 2 OH 2 , OH AB 30
2
SH 2 40 2 30 2 50 2 ; SH 50
1
S бок. Pосн. SН
2
Pосн . 4 АВ 4 60 240
1
S бок. 240 50 600
2
S осн . АВ 2 60 2 3600
S полн. S бок. S осн. 600 3600 4200.
18.
№17Найдите площадь боковой поверхности правильной
четырехугольной пирамиды, сторона основания которой равна
60 и высота равна 40.
Решение.
S
40
С
D
30
O
A
60
B
Н
В правильной пирамиде боковые
грани равнобедренные треугольники ,
SH высота и медиана одного из них
В п / у SOH по т. Пифагора
1
SH 2 SO 2 OH 2 , OH AB 30
2
SH 2 40 2 30 2 50 2 ; SH 50
1
S бок. Pосн. SН
2
Pосн . 4 АВ 4 60 240
S бок.
Ответ: 600.
1
240 50 600.
2
19.
№18Во сколько раз увеличится площадь поверхности пирамиды, если
все её ребра увеличить в 10 раз?
Решение.
S
Площади подобных тел относятся
как квадрат коэффициента подобия
S2
k 2 10 2 100 .
S1
А
С
O
В
Ответ: 100.
20.
№19Ребра тетраэдра равны 10. Найдите площадь
проходящего через середины четырех его ребер.
S
Q
P
А
O
M
N
сечения,
Решение.
Стороны сечения средние линии
равносторонних треугольников
( граней ), противолежащие ребра
взаимнопер пендикуляр ны, значит ,
сечение квадрат, со стороной,
С равной половине ребра
S MNPQ MN 2 52 25.
В
Ответ: 25.
21.
№20Найдите объём пирамиды, высота которой равна 60, а
основание – прямоугольник со сторонами 30 и 40.
Решение.
S
Sосн. АВ BC 40 30 1200
1
1
Vпир. Sосн. h 1200 60 2400.
3
3
60
С
D
30
O
A
40
B
Ответ: 2400.
22.
№21В правильной четырехугольной пирамиде высота равна 120,
объём равен 20000. Найдите боковое ребро этой пирамиды.
S
120
D
O
A
1
3V
Решение. Vпир. S осн. h S осн.
3
h
3 20000
S осн .
500
120
S осн . a 2 500 a 500 10 5
1
АО
АС , где АС а 2 ,
С
2
а 2 10 5 2
АО
5 10
2
2
B
В п / у ASO по т. Пифагора
AS 2 AO 2 OS 2
Ответ: 130.
2
AS 5 10 120 2 130 2
AS 130.
2
23.
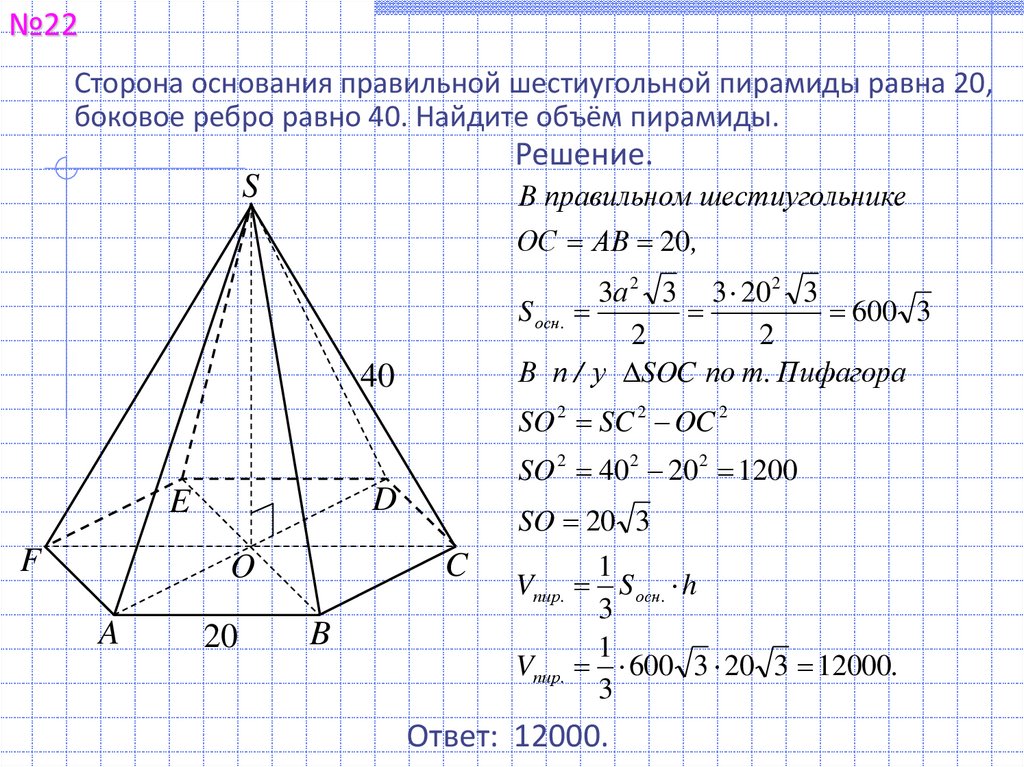
№22Сторона основания правильной шестиугольной пирамиды равна 20,
боковое ребро равно 40. Найдите объём пирамиды.
Решение.
S
В правильном шестиугольнике
ОС АВ 20 ,
3а 2 3 3 20 2 3
S осн .
600 3
2
2
В п / у SOC по т. Пифагора
40
SO 2 SC 2 OC 2
SO 2 40 2 20 2 1200
D
E
F
C
O
A
20
B
SO 20 3
1
Vпир. S осн. h
3
1
Vпир. 600 3 20 3 12000.
3
Ответ: 12000.
24.
№23Объём правильной шестиугольной пирамиды 6000.
Сторона основания равна 10. Найдите боковое ребро.
Решение.
В правильном шестиугольнике
ОС АВ 10 ,
S
3а 2 3 3 10 2 3
S осн.
150 3
2
2
3Vпир.
1
Vпир. S осн. h h
3
S осн.
h
D
E
F
C
O
A
10
B
3 6000
40 3 SO
150 3
В п / у SOC по т. Пифагора
h
SC 2 SO 2 OC 2
2
SC 40 3 10 2 4900
SO 70.
2
Ответ: 70.
25.
№24Сторона основания правильной шестиугольной пирамиды равна
40, а угол между боковой гранью и основанием равен 45°.
Найдите объём пирамиды.
Решение.
S
В правильном шестиугольнике
а 3 40 3
OH
20 3
2
2
3а 2 3 3 40 2 3
S осн.
2400 3
2
2
SOH п / у , р / б
h
E
D
45°
F
O
A
40
Н
B
C
SO OH 20 3
1
Vпир. S осн. h
3
1
Vпир. 2400 3 20 3 4800.
3
Ответ: 4800.
26.
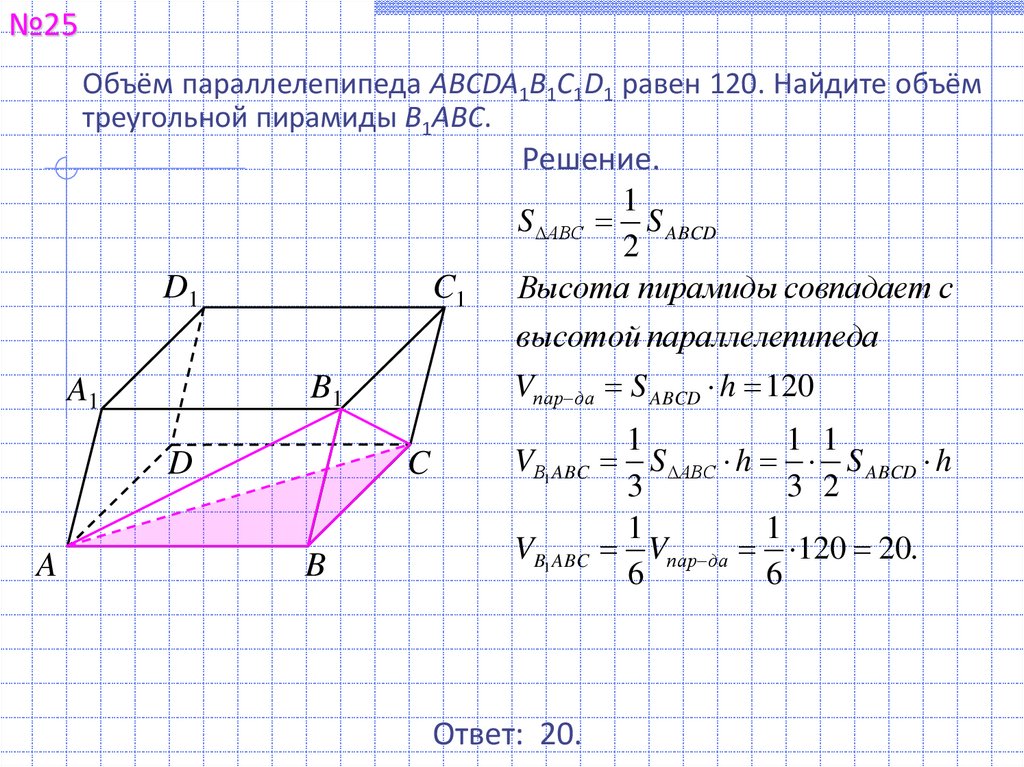
№25Объём параллелепипеда ABCDA1B1C1D1 равен 120. Найдите объём
треугольной пирамиды B1ABC.
B1
Решение.
1
S АВС S ABCD
2
Высота пирамиды совпадает с
высотой параллелепипеда
Vпар да S ABCD h 120
B
1
1 1
VВ1 ABC S АВС h S ABCD h
3
3 2
1
1
VB1 ABC Vпар да 120 20.
6
6
D1
A1
C1
D
A
C
Ответ: 20.
27.
№26Объём куба равен 12000. Найдите объём четырехугольной
пирамиды, основанием которой является грань куба, а
вершиной – центр куба.
Решение.
D1
A1
C1
B1
М
D
A
C
B
1
S ABCD h
3
Высота пирамиды равна половине
1
высоты параллелепипеда h a
2
Vпар да a 3 12000
VМАВСD
1
1
1
1
S ABCD h a 2 a a 3
3
3
2
6
1
1
VМАВСD Vпар да 12000 2000 .
6
6
VМАВСD
Ответ: 2000.
28.
№27Объём параллелепипеда ABCDA1B1C1D1 равен 4500. Найдите объём
треугольной пирамиды AD1CB1.
Решение (см. анимацию)
D1
A1
C1
B1
C
D
A
B
Чтобы получить искомую пирамиду,
отделим от параллелепипеда четыре
одинаковые пирамиды, как на рисунке.
Объём каждой такой пирамиды равен
1
1 1
1
V ABCB1 S ABC h S ABCD h Vпар да
3
3 2
6
Vпар да S ABCD h 4500
1
V АD1СВ1 Vпар да 4V ABCB1 Vпар да 4 Vпар да
6
1
4
V АD1СВ1 1 Vпар да Vпар да
3
6
1
V АD1СВ1 4500 1500 .
3
Ответ: 1500.
29.
№28Объём тетраэдра равен 19000. Найдите объём многогранника,
вершинами которого являются середины рёбер данного тетраэдра.
Решение.
S
Объемы подобных тел относятся
как куб коэффицент а подобия
3
М
VSMNP
1
1
1
k 3 VSMNP VSABC
VSABC
8
8
2
P
N
А
С
В
Чтобы получить искомую фигуру,
отделим от тетраэдра четыре
одинаковые пирамиды, как на рисунке
1
Vоктаэдра VSABC 4VSMNP VSABC 4 VSABC
8
1
1
Vоктаэдра 1 VSABC VSABC
2
2
1
Vоктаэдра 19000 9500 .
2
Ответ: 9500.
30.
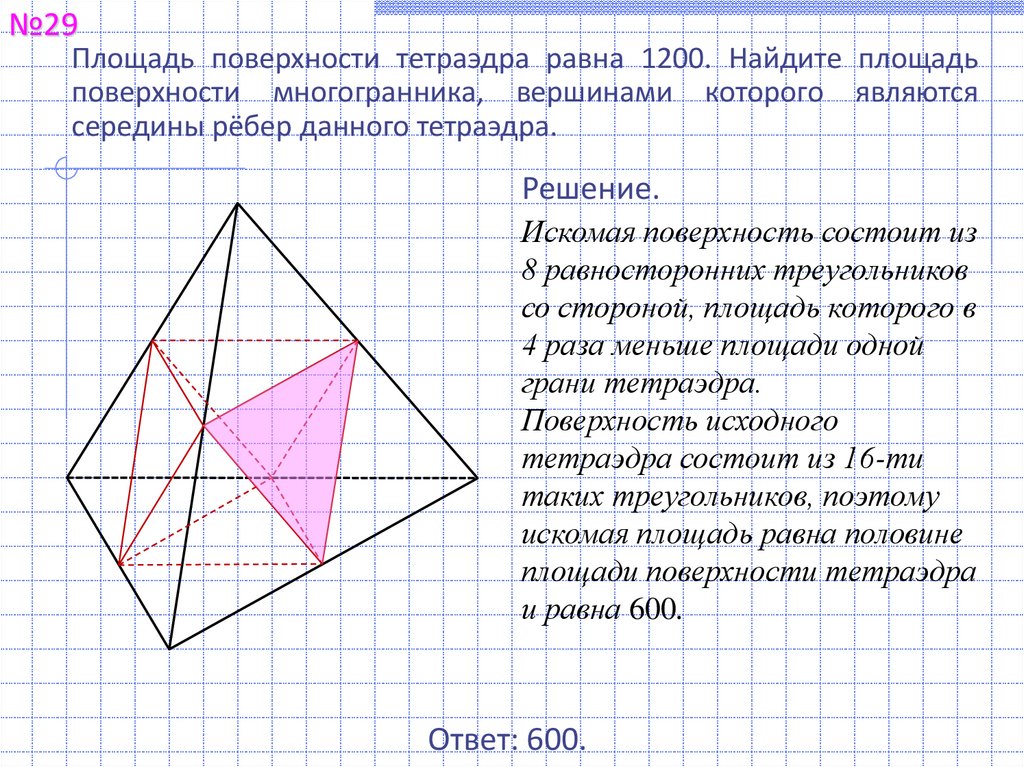
№29Площадь поверхности тетраэдра равна 1200. Найдите площадь
поверхности многогранника, вершинами которого являются
середины рёбер данного тетраэдра.
Решение.
Искомая поверхность состоит из
8 равносторонних треугольников
со стороной, площадь которого в
4 раза меньше площади одной
грани тетраэдра.
Поверхность исходного
тетраэдра состоит из 16-ти
таких треугольников, поэтому
искомая площадь равна половине
площади поверхности тетраэдра
и равна 600.
Ответ: 600.
31.
№30Найдите объём параллелепипеда ABCDA1B1C1D1, если объём
треугольной пирамиды ABDA1 равен 30.
Решение.
D1
A1
B1
C1
A
D
C
B
1
S АВD S ABCD
2
Высота пирамиды совпадает с
высотой параллелепипеда
Vпар да S ABCD h
1
1 1
S АВD h S ABCD h
3
3 2
1
V ABDA1 Vпар да Vпар да 6V ABDA1
6
Vпар да 6 30 180 .
V ABDA1
Ответ: 180.
32.
№31В правильной четырехугольной пирамиде SABCD точка О –
центр основания, S – вершина, SO = 40, AC = 60. Найдите
боковое ребро SC.
S
Решение.
1
1
АО АС 60 30 ,
2
2
В п / у ASO по т. Пифагора
40
D
30
A
30
O
С
AS 2 AO 2 OS 2
AS 2 30 2 40 2 50 2
AS 50 .
B
Ответ: 50.
33.
№32В правильной четырехугольной пирамиде SABCD точка О – центр
основания, S – вершина, SA = 50, AC = 60. Найдите длину отрезка SO.
S
Решение.
1
1
АО АС 60 30 ,
2
2
В п / у ASO по т. Пифагора
50
D
30
A
30
O
С
SO 2 AS 2 AO 2
SO 2 50 2 30 2 40 2
SO 40 .
B
Ответ: 40.
34.
№33В правильной четырехугольной пирамиде SABCD точка О – центр
основания, S – вершина, SO = 40, SA = 50. Найдите длину отрезка AC.
S
Решение.
В п / у ASO по т. Пифагора
AO 2 AS 2 SO 2
50
40
С
D
AO 2 50 2 40 2 30 2
AO 40 , AC 2 AO 2 30 60 .
O
A
B
Ответ: 60.
35.
№34В правильной четырёхугольной пирамиде SABCD с основанием
ABCD боковое ребро SA равно 50, сторона основания равна 30√2.
Найдите объём пирамиды.
Решение.
S
Основание пирамиды квадрат ABCD ,
в котором AO
С
D
O
A
30 2
30 2
30
2
2
В п / у ASО по т. Пифагора
h
50
AB
B
SО 2 SА 2 AO 2
SO 2 50 2 30 2 40 2
SO 40
S осн. АВ 2 30 2
1800
2
1
S осн. h
3
1
Vпир. 1800 40 24000 .
3
Vпир.
Ответ: 24000.
36.
№35В правильной четырёхугольной пирамиде все рёбра равны 10.
Найдите площадь сечения пирамиды плоскостью, проходящей
через середины боковых рёбер.
S
Решение.
Q
M
P
N
С
D
O
A
MNPQ - квадрат со стороной, равной
половине стороны основания пирамиды.
Площади подобных фигур относятся
как квадрат коэффициента подобия
10
B
2
1
1
k
S ABCD
4
2
1
1
S MNPQ S ABCD 10 2 25 .
4
4
S MNPQ
Ответ: 25.
2
37.
№36В правильной треугольной пирамиде боковое ребро равно 50, а
сторона основания равна 30√3. Найдите высоту пирамиды.
Решение.
S
Основание пирамиды р / с ABC ,
в котором AO
AB
30
3
3
В п / у ASО по т. Пифагора
50
h
SО 2 SА 2 AO 2
А
С
O
30 3
SO 2 50 2 30 2 40 2
SO 40 .
30 3
В
Ответ: 40.




























 Математика
Математика