Похожие презентации:
Вычисление углов между прямыми и плоскостями
1.
Геометрия 11 класс• Тема урока: Вычисление углов между
прямыми и плоскостями
• Учитель: Степанова Елена Борисовна
2021
2.
Угол между прямыми, лежащими в одной плоскости3.
Угол между скрещивающимися прямыми4.
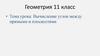
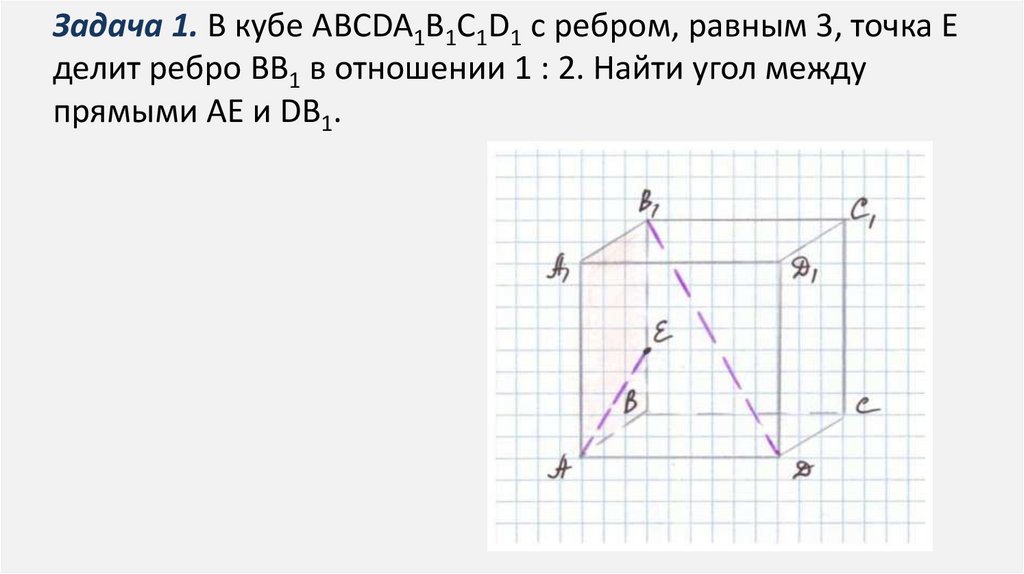
Задача 1. В кубе ABCDA1B1C1D1 с ребром, равным 3, точка Еделит ребро ВВ1 в отношении 1 : 2. Найти угол между
прямыми АЕ и DB1.
5.
6.
7.
Направляющий вектор• Ненулевой вектор называется
направляющим вектором прямой а, если он
лежит либо на прямой а, либо на прямой,
параллельной прямой а.
8.
Алгоритм нахождения величины угла междупрямыми
•Выбрать направляющие векторы для данных прямых.
•Вычислить координаты направляющих векторов.
•Найти cos φ =
9.
Задача 2. Вершины тетраэдра АВСD имеют координатыА(3;-1;0), В(0;-7;3), С(-2;1;-1), D(3;2;6). Доказать , что прямая АВ
перпендикулярна плоскости ADC.
10.
Задача 3.Дан куб АВСDA1 B1C1D1. 0 – центр граниАВСD. Найти угол между прямыми ВО и А1D.
11.
12.
Задача 4.В прямоугольном параллелепипеде АВСDA1B1C1D1АВ = ВС = ½ АА1. Найти угол между прямыми ВD и CD1.
13.
Чтобы найти угол между прямой и плоскостьюнужно найти координаты ненулевого вектора,
перпендикулярного к плоскости.
14.
Угол между плоскостями равен углу междупрямыми, перпендикулярными этим плоскостям
15.
Решите задачи1. Даны координаты точек
А(1;-1;-4), В(-3;-1;0),
С(-1;2;5), D(2;-3;1). Найти
косинус угла между
векторами .
2. Дан куб АВСDA1 B1C1D1.
Найти угол между
прямыми АD1 и ВК, где К –
середина ребра DD1.
16.
Санкт-Петербургская академия постдипломного педагогического образованияУспешной работы!














 Математика
Математика