Вычисление углов между прямыми и плоскостями с помощью скалярного произведения

1. 26.05.20 Вычисление углов между прямыми и плоскостями с помощью скалярного произведения

2.

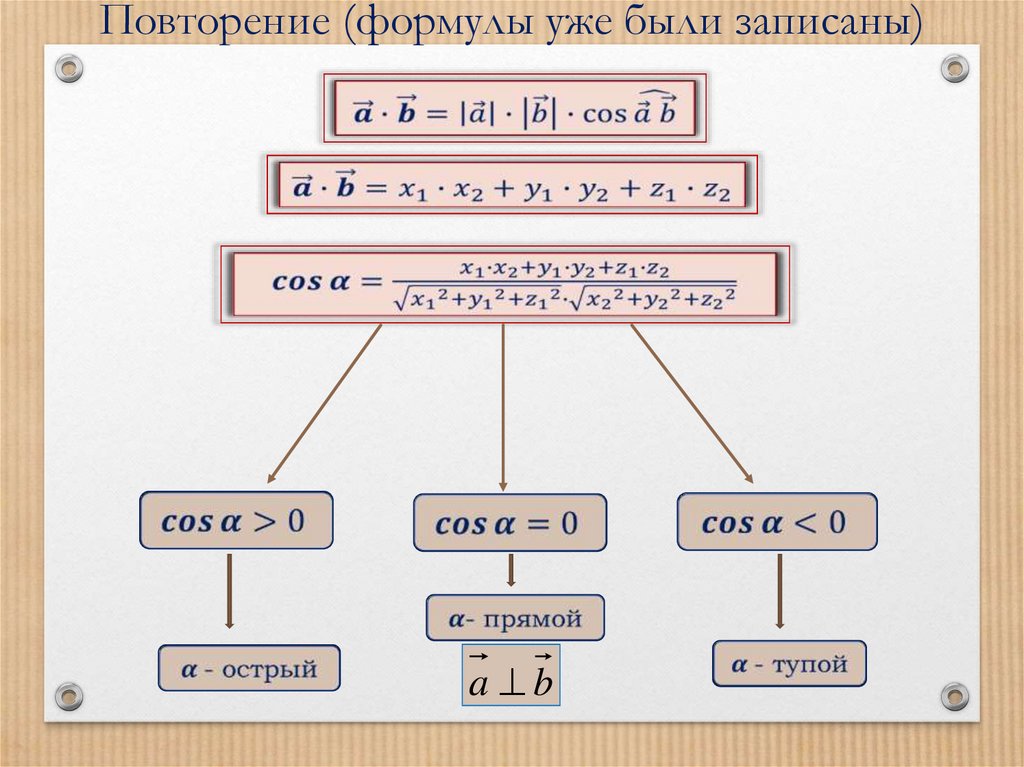
Повторение (формулы уже были записаны)
a b

3. 1) Направляющий вектор прямой.

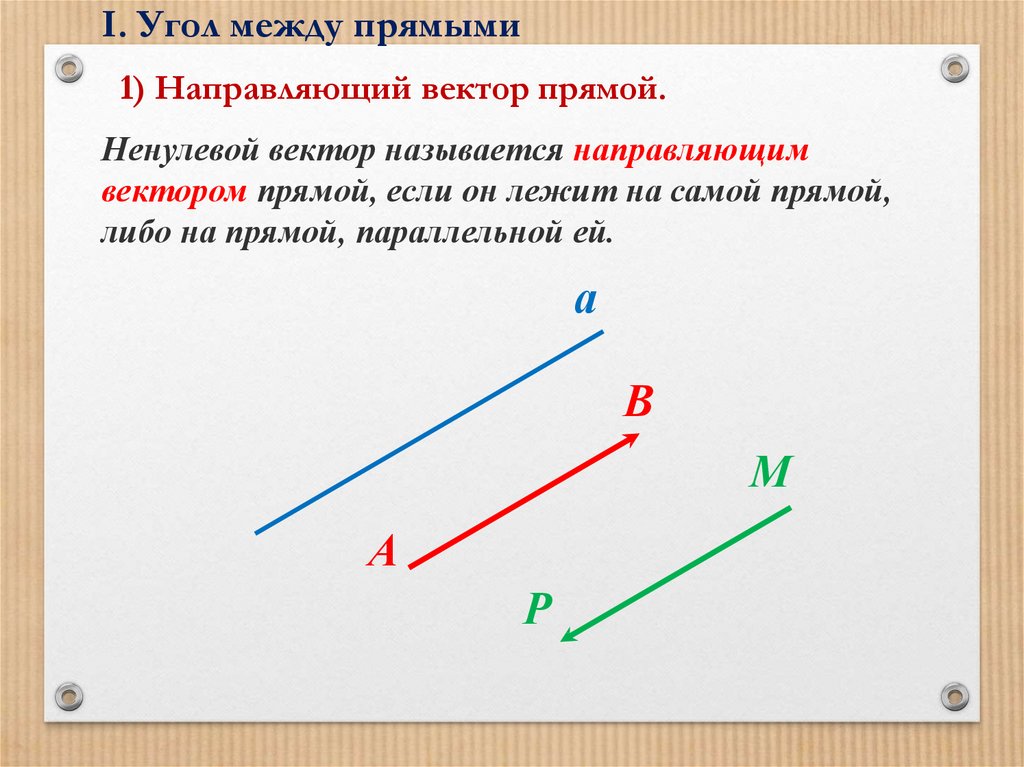
I. Угол между прямыми
1) Направляющий вектор прямой.
Ненулевой вектор называется направляющим
вектором прямой, если он лежит на самой прямой,
либо на прямой, параллельной ей.
а
В
М
А
Р

4.

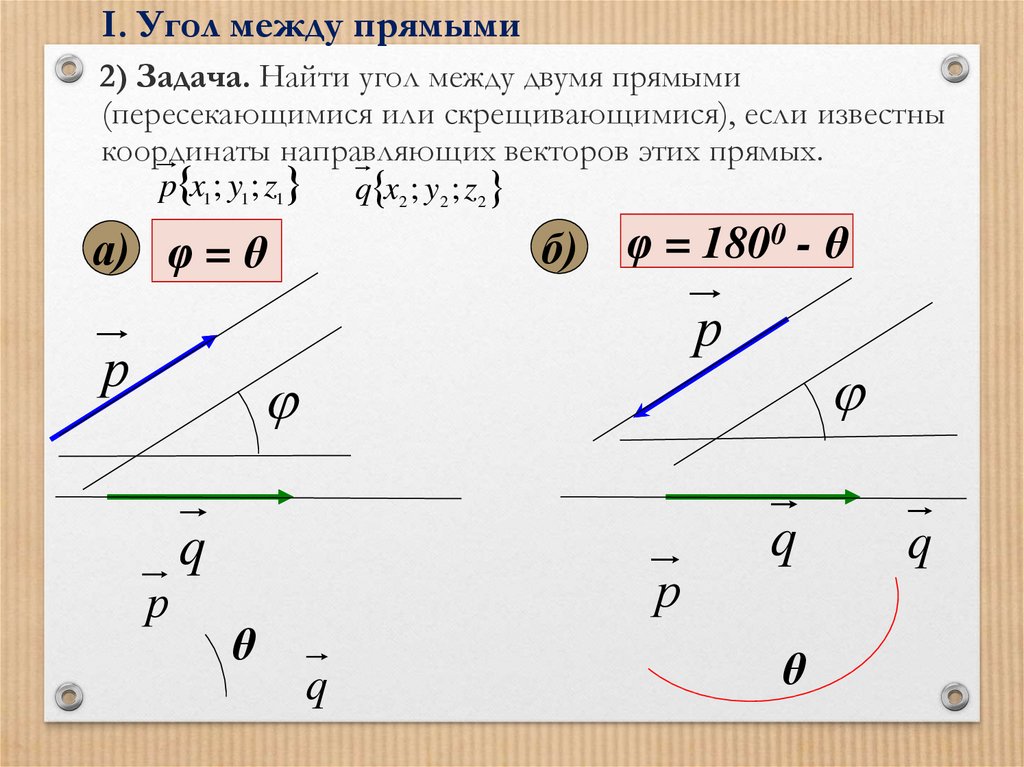
I. Угол между прямыми
2) Задача. Найти угол между двумя прямыми
(пересекающимися или скрещивающимися), если известны
координаты направляющих векторов этих прямых.
p x1; y1; z1
q x2 ; y2 ; z2
б)
а) φ = θ
φ = 1800 - θ
р
р
q
р
р
θ
q
q
θ
q

5.

I. Угол между прямыми
Вывод: если
р - направляющий вектор прямой а, p x1; y1; z1
q - направляющий вектор прямой b, q x2 ; y2 ; z2
то
φ=θ
или
φ = 1800 - θ
Значит,
cos =
| x1 x2 + y1 y2 + z1 z 2 |
x12 + y12 + z12 x22 + y22 + z 22
где p x1; y1; z1 и q x2 ; y2 ; z2 - направляющие векторы прямых.

6.

I. Угол между прямыми
Пример 1.
Вычислить угол между прямыми AB и CD, если:
а) A(5;-8;-1), В(6;-8;-2), С(7;-5;-11), D(7;-7;-9)
Решение.
1) Найдем координаты направляющих векторов прямых АВ и СD.
AB 1;0; 1
2) cos =
cos =
СD 0; 2;2
| x1 x2 + y1 y2 + z1 z 2 |
А
С
x12 + y12 + z12 x22 + y22 + z 22
| 1 0 0 ( 2) ( 1) 2 |
12 0 2 ( 1) 2 0 2 ( 2) 2 2 2
0
1
60
cos
2
б) A(1; 0; 2), В(2; 1; 0), С(0; -2; -4), D(-2; -4; 0);
в) A(-6; -15; 7), В(-7; -15; 8), С(14; -10; 9), D(14; -10; 7).
В
D

7.

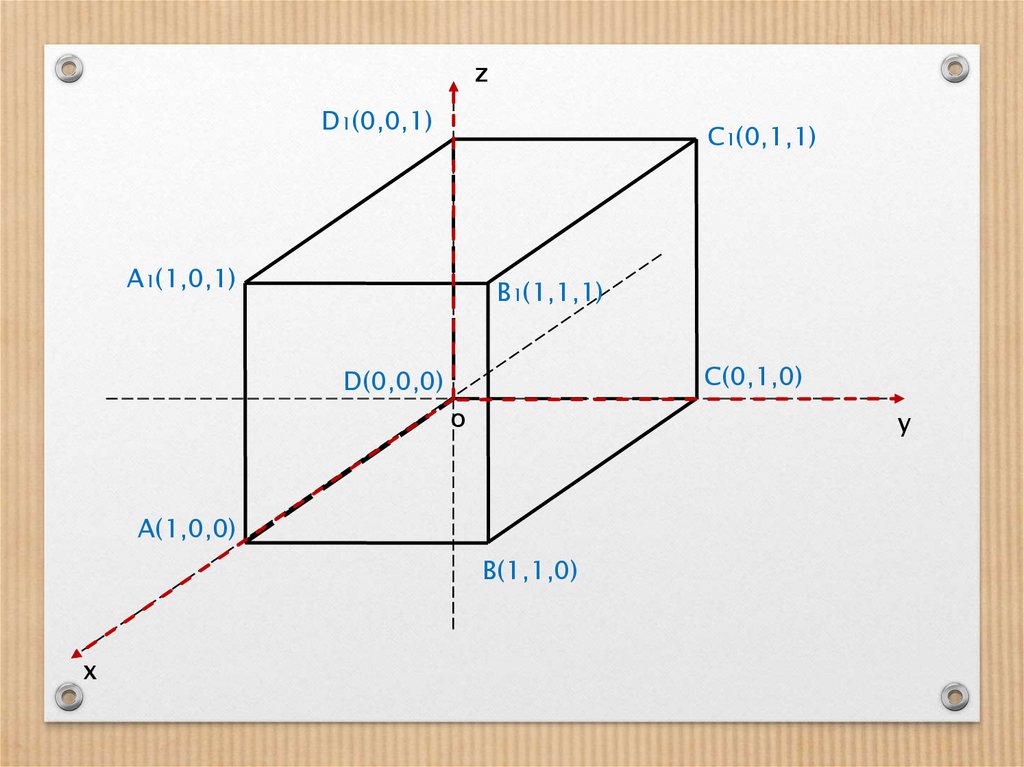
z
D1(0,0,1)
C1(0,1,1)
A1(1,0,1)
B1(1,1,1)
C(0,1,0)
D(0,0,0)
o
y
A(1,0,0)
B(1,1,0)
x

8.

I. Угол между прямыми
Пример 2.
Дано: ABCDA1B1C1D1 куб
z
С1
D1
B1
А1
С
D
у
х
А
B
в) между прямыми АС и D1B, АВ1 и ВС1, А1D и АС1;
г) между прямыми А1В и D1N, где N – середина ВВ1.

9.

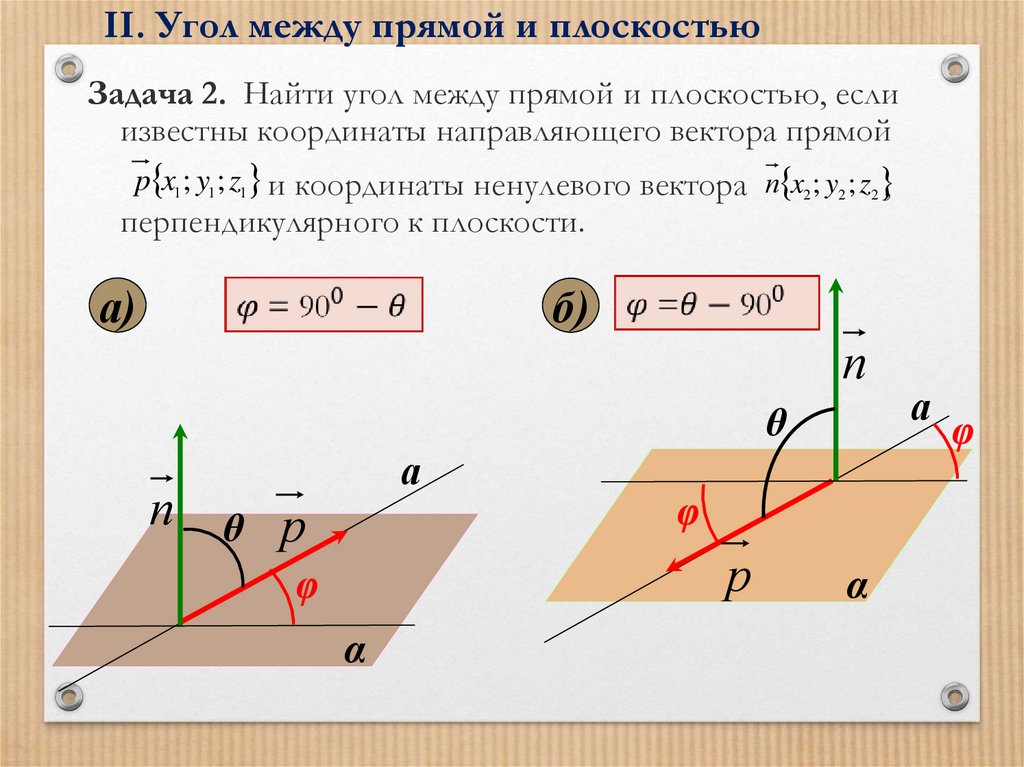
II. Угол между прямой и плоскостью
Задача 2. Найти угол между прямой и плоскостью, если
известны координаты направляющего вектора прямой
p x1; y1; z1 и координаты ненулевого вектора п x2 ; y2 ; z2 ,
перпендикулярного к плоскости.
а)
б)
п
θ
п
а
θ
р
φ
р
φ
α
α
а
φ

10.

II. Угол между прямой и плоскостью
Вывод: если
р - направляющий вектор прямой а, p x1; y1; z1
п x2 ; y2 ; z2
или
то
Значит,
cos
sin =
| x1 x2 + y1 y2 + z1 z 2 |
x12 + y12 + z12 x22 + y22 + z 22
где p x1; y1; z1 и п x2 ; y2 ; z2 .

11.

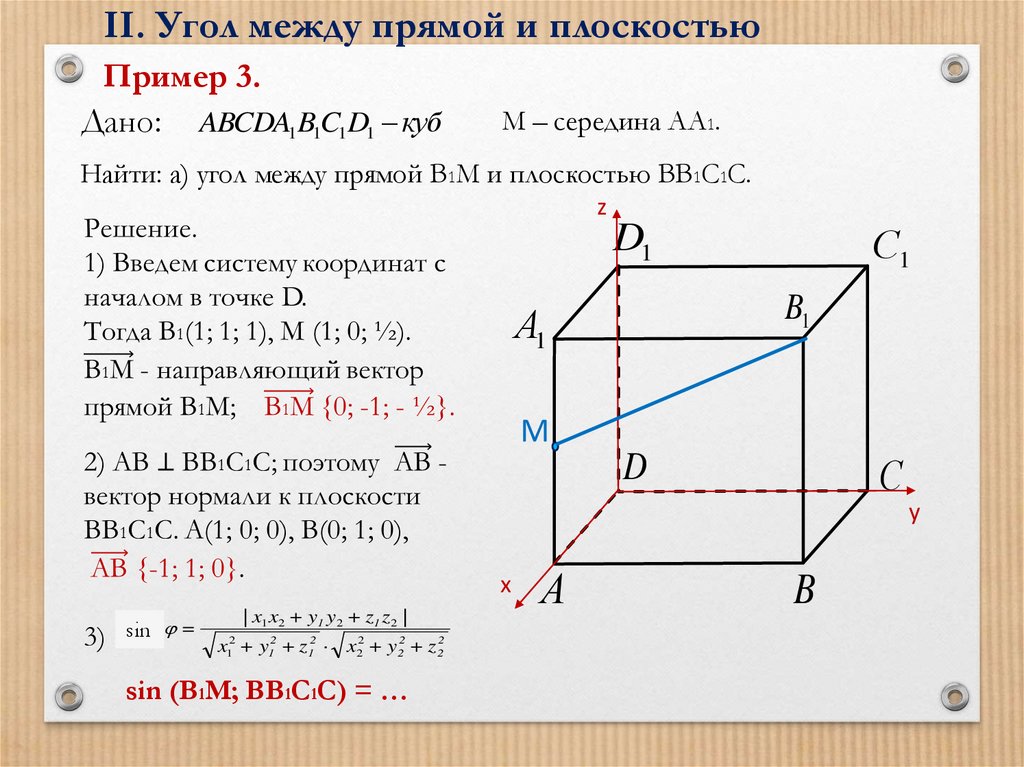
II. Угол между прямой и плоскостью
Пример 3.
Дано: ABCDA1B1C1D1 куб
М – середина АА1.
Найти: а) угол между прямой В1М и плоскостью ВВ1С1С.
z
С1
D1
B1
А1
М
С
D
у
х
cos =
sin
| x1 x2 + y1 y2 + z1 z 2 |
x12 + y12 + z12 x22 + y22 + z 22
sin (В1М; ВВ1С1С) = …
А
B