Скалярное_произведение_и_углы_Сентябрь

1. Скалярное произведение. Вычисление углов между прямыми

Геометрия 11 класс

2. Угол между векторами.

b
ОА а ОВ b
ab
Если а b, то аb 0
а
0
0
0
А
α
О
В
Если а b ,то ab 180
Если а b ,то ab 90

3. Скалярное произведение векторов.

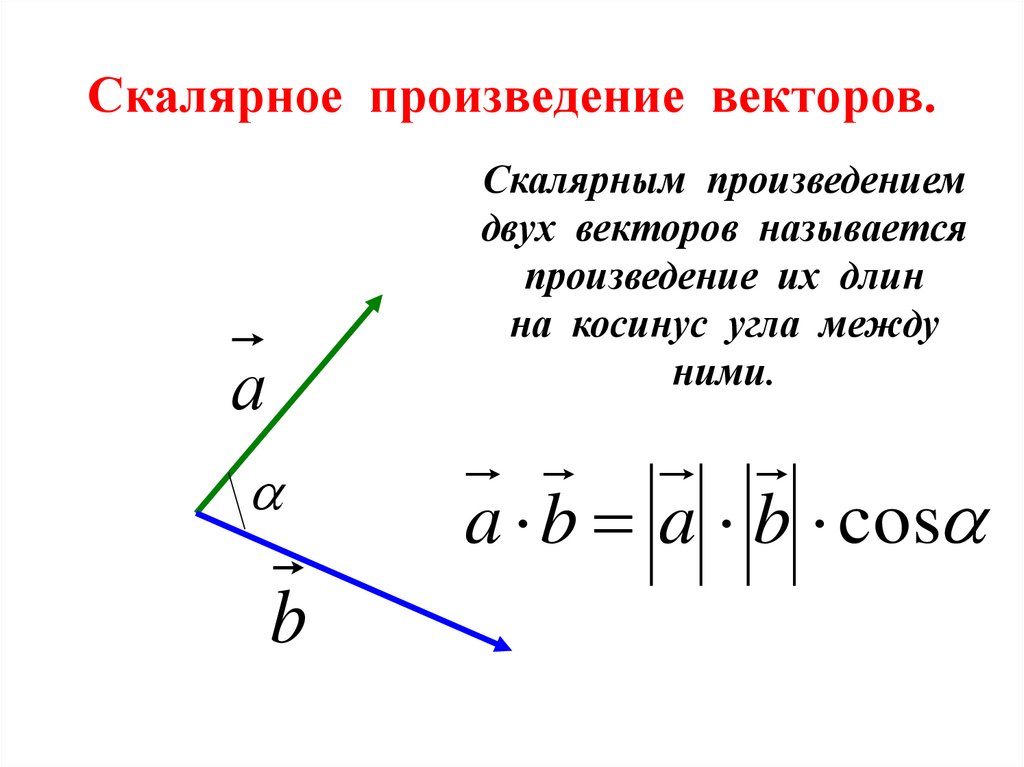
Скалярным произведением
двух векторов называется
произведение их длин
на косинус угла между
ними.
а
b
a b a b cos

4. Скалярный квадрат вектора Из формулы скалярного произведения векторов

a1 a2 | a1 | | a2 | cos .
получаем, что вектор можно умножать на сам этот
вектор. Такое произведение называется скалярным
квадратом и обозначается a 2 .
Из формулы скалярного произведения следует
равенство a 2 | a |2 . Это равенство часто
используется для вычисления длины вектора.

5. Скалярное произведение векторов в координатах

Для скалярного произведения векторов имеет
место формула a1 a2 x1 x2 y1 y2 z1 z2 .
где a1 ( x1 , y1 , z1 ) и a2 ( x2 , y2 , z2 ) координаты данных векторов.

6. Упражнение

Найдите скалярное произведение векторов
a1(-1, 2, 3) и a2 (2, -1, 0).
Ответ: –4.

7. Перпендикулярность векторов. Если векторы перпендикулярны, то угол между ними прямой, его косинус равен нулю, следовательно, из

формулы
a1 a2 | a1 | | a2 | cos .
можно получить, что и скалярное
произведение равно нулю.
a b a b 0
Верно ли обратное?

8. Упражнение

При каком значении z векторы a 3i 5 j zk и
b 4i 2 j k перпендикулярны?
Ответ: z = -2.

9. Упражнение

Найдите координаты единичного вектора, если
известно, что он перпендикулярен векторам с
координатами (1,1,0), (0,1,1).
Ответ: (
3
3 3
3 3
3
,
,
), (
,
,
).
3
3 3
3 3
3

10. Свойства скалярного произведения

Для скалярного произведения векторов
справедливы свойства, аналогичные свойствам
произведения чисел:
1.
a b b a.
2.
(ta ) b t (a b ).
3.
( a b )c a c b c .
Обладает ли скалярное произведение
ассоциативностью?

11. Угол между векторами

a1 a2
Используя формулу cos
,
| a1 | | a2 |
и формулу скалярного произведения, можно
находить угол между векторами.
Из этой формулы можно видеть: если
скалярное произведение отрицательно, то
угол между векторами тупой.

12.

Вычисление угла между векторами
cos
x1 x2 y1 y 2 z1 z 2
x12 y12 z12
x22 y 22 z 22

13. Упражнение

Найдите угол между векторами:
а) a1 (2, 3, -1) и a2 (1, -2, 4);
б) a1(1, 2, -2) и a2(1, 0, -1).
4 6
Ответ: а) cos
21
; б) = 45о.

14. Упражнение

Найдите углы, которые образует с координатными
векторами вектор:
а) i j k ;
б) 3 j k ;
в) 5i ;
г) a (0, 3, 4).
3
3 10
10
о
; б) 90 , cos
, cos
;
Ответ: а) cos
3
10
10
3
4
о
о
о
о
в) 180 , 90 , 90 ; г) 90 , cos , cos .
5
5

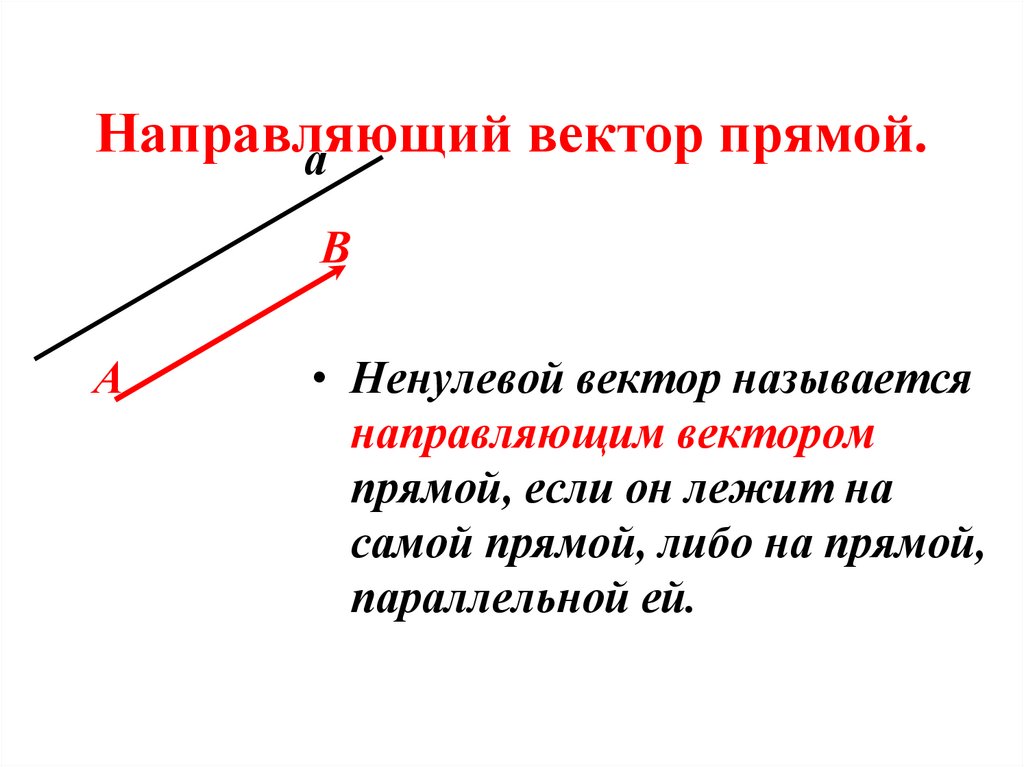
15. Направляющий вектор прямой.

а
В
А
• Ненулевой вектор называется
направляющим вектором
прямой, если он лежит на
самой прямой, либо на прямой,
параллельной ей.

16.

Найти угол между двумя прямыми
(пересекающимися или скрещивающимися), если
известны координаты направляющих векторов этих
прямых.
p x1; y1; z1
а)
р
б)
q x2 ; y2 ; z2
р
q
р
р
θ
q
φ=θ
φ = 1800 - θ
q
θ
q

17.

Угол между прямыми в пространстве
cos
x 1 x 2 y 1 y 2 z1 z 2
x y z x y z
где p x 1 ; y 1 ; z1
2
1
2
1
2
1
2
2
2
2
и q x ; y ; z —
2
2
2
— направляющие векторы прямых
2
2
,

18.

Дано: А 3; 2;4 В 4; 1;2 С 6; 3;2
D 7; 3;1
Найти: угол между прямыми АВ и CD.
1. Найдем координаты векторов
АВ
1;1; 2
CD 1;0; 1
2. Воспользуемся формулой:
cos
x1 x2 y1 y 2 z1 z 2
x y z x y z
2
1
2
1
2
1
2
2
2
2
2
2
φ = 300

19.

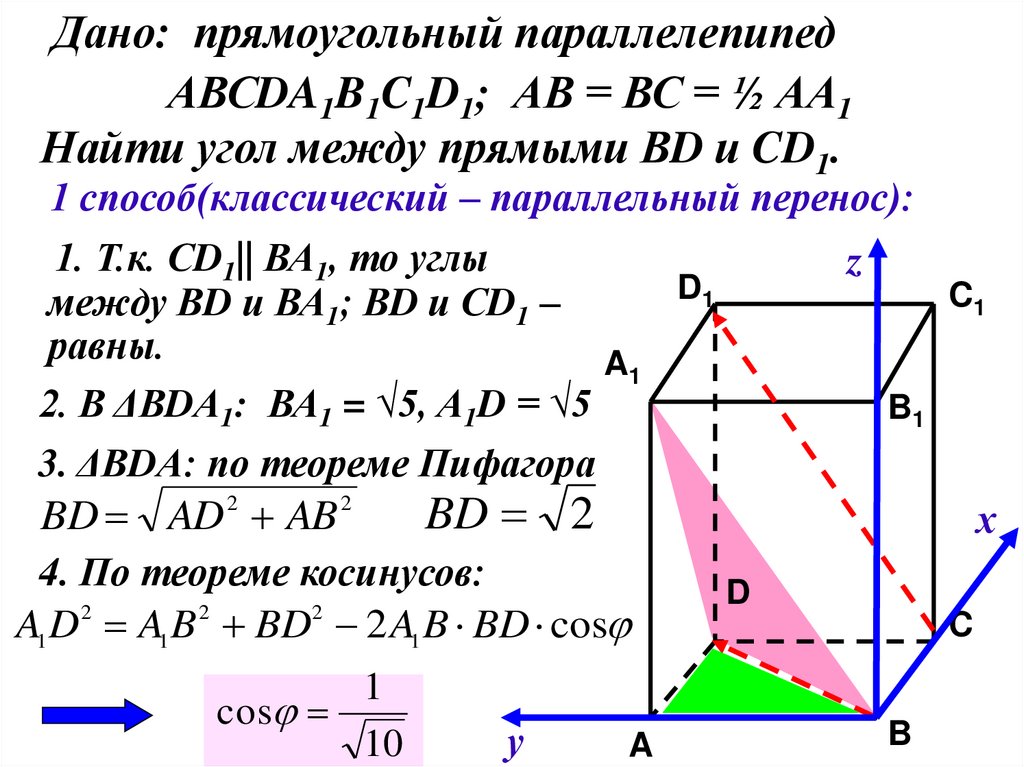
Дано: прямоугольный параллелепипед
АВСDA1B1C1D1; АВ = ВС = ½ АА1
Найти угол между прямыми ВD и CD1.
1 способ(классический – параллельный перенос):
1. Т.к. СD1|| ВА1, то углы
D1
между ВD и ВА1; ВD и СD1 –
равны.
A1
2. В ΔВDА1: ВА1 = √5, А1D = √5
3. ΔВDА: по теореме Пифагора
BD AD AB
2
2
C1
B1
BD 2
х
4. По теореме косинусов:
A1 D 2 A1 B 2 BD2 2 A1 B BD cos
1
cos
10
z
у
A
D
C
B

20.

Дано: прямоугольный параллелепипед
АВСDA1B1C1D1; АВ = ВС = ½ АА1
Найти угол между прямыми ВD и CD1.
2 способ (векторно-координатный):
z
1. Введем систему координат Bxyz D1
2. Пусть АА1= 2, тогда
A1
АВ = ВС = 1.
C1
B1
В 0;0;0 С 1;0;0 D 1;1;0 D1 1;1;2
3. Координаты векторов:
ВD 1;1;0
CD1 0;1;2
4. Находим косинус угла между
прямыми:
1
cos
10
у
A
х
D
C
B

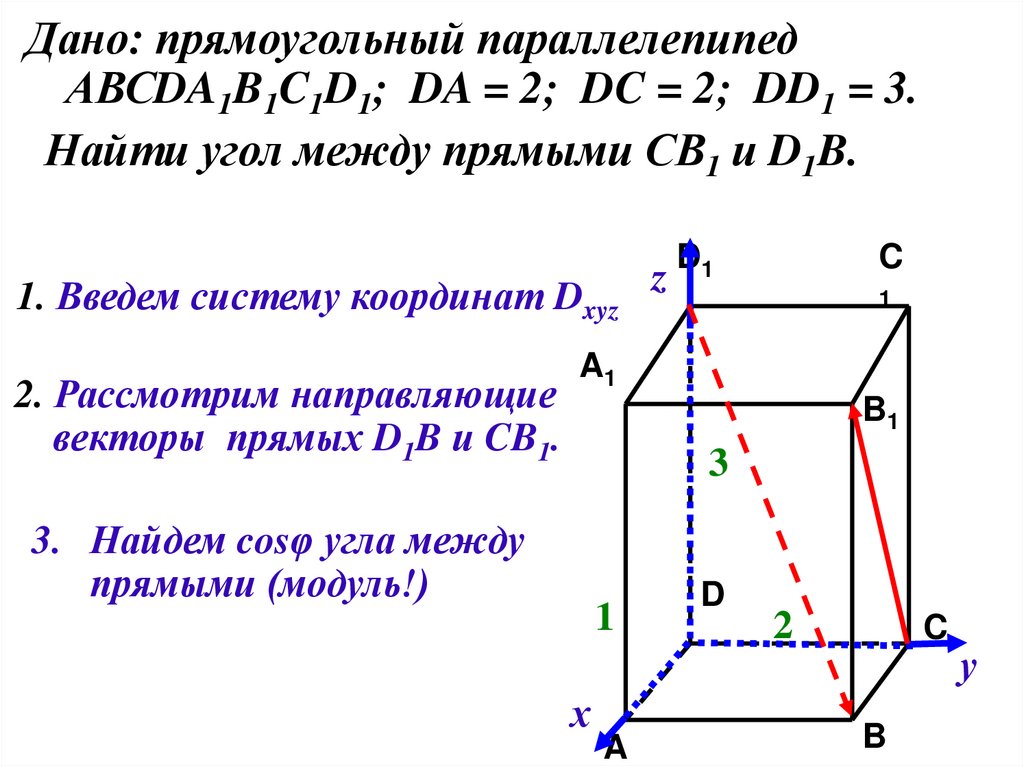
21.

Дано: прямоугольный параллелепипед
АВСDA1B1C1D1; DA = 2; DC = 2; DD1 = 3.
Найти угол между прямыми СВ1 и D1B.
1. Введем систему координат Dxyz z
2. Рассмотрим направляющие
векторы прямых D1B и CB1.
D1
C
1
A1
B1
3
3. Найдем cosφ угла между
прямыми (модуль!)
1
х
A
D
2
C
B
у

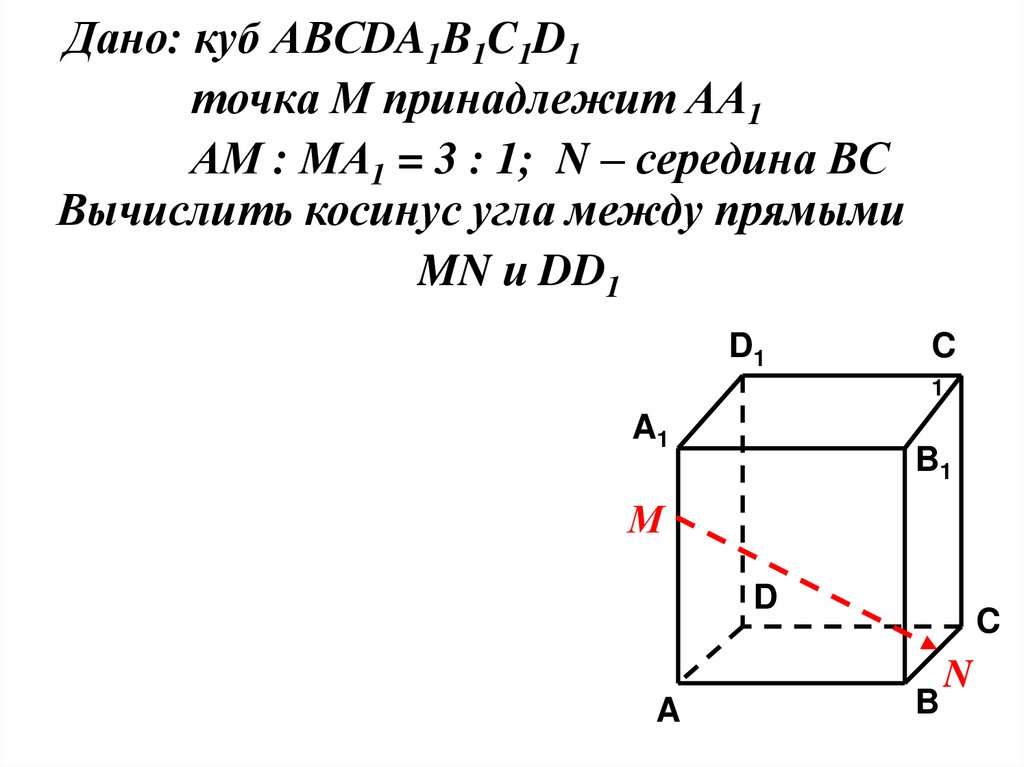
22.

Дано: куб АВСDA1B1C1D1
точка М принадлежит АА1
АМ : МА1 = 3 : 1; N – середина ВС
Вычислить косинус угла между прямыми
MN и DD1
D1
C
1
A1
B1
М
D
A
C
B
N

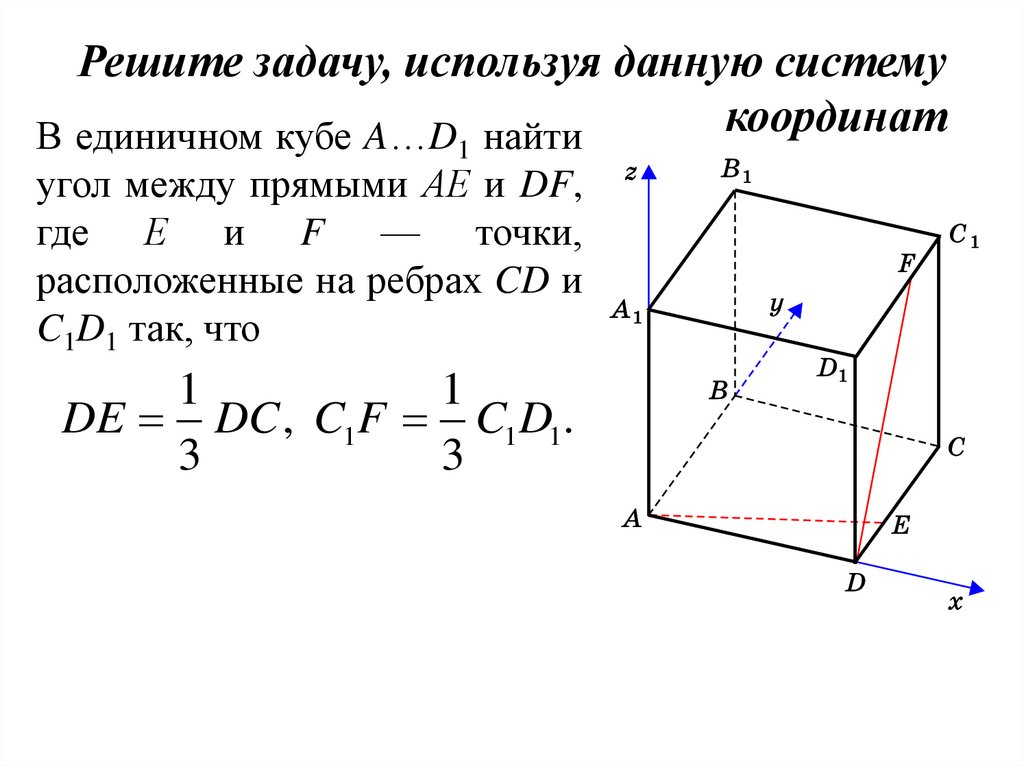
23.

Решите задачу, используя данную систему
координат
В единичном кубе A…D найти
1
угол между прямыми АЕ и DF,
где Е и F — точки,
расположенные на ребрах CD и
C1D1 так, что
1
1
DE DC , C1F C1D1.
3
3