Похожие презентации:
Algorithms and data structures. Dynamic programming (lecture 10)
1.
ALGORITHMS AND DATA STRUCTURESLECTURE 10 – INTRO TO DYNAMIC PROGRAMMING
Aigerim Aibatbek
Aigerim.aibatbek@astanait.edu.kz
2.
WHAT IS DYNAMIC PROGRAMMING?Wikipedia definition: “method for solving complex problems by breaking them
down into simpler subproblems”.
*wait, doesn't that look like a divide and conquer algorithm?
Divide and Conquer method:
1.
Divide the problem into independent sub-problem
2. Solve the sub-problem recursively
3. Combine their solutions to solve the original problem
3.
WHAT IS DYNAMIC PROGRAMMING?Whereas, Dynamic Programming is applicable when the sub-problems are not
independent.
Dynamic Programming is a way of improving on inefficient divide-and-conquer
algorithms, i.e. it is optimization over recursion.
* by “inefficient”, we mean that the same recursive calls are made over and over.
4.
EXAMPLE: FIBONACCI SERIESLet`s consider the Calculation of Fibonacci numbers: F(n) = F(n-2) + F(n-1),
with seed values F(0) = 0, F(1) = 1
Series looks like:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
5.
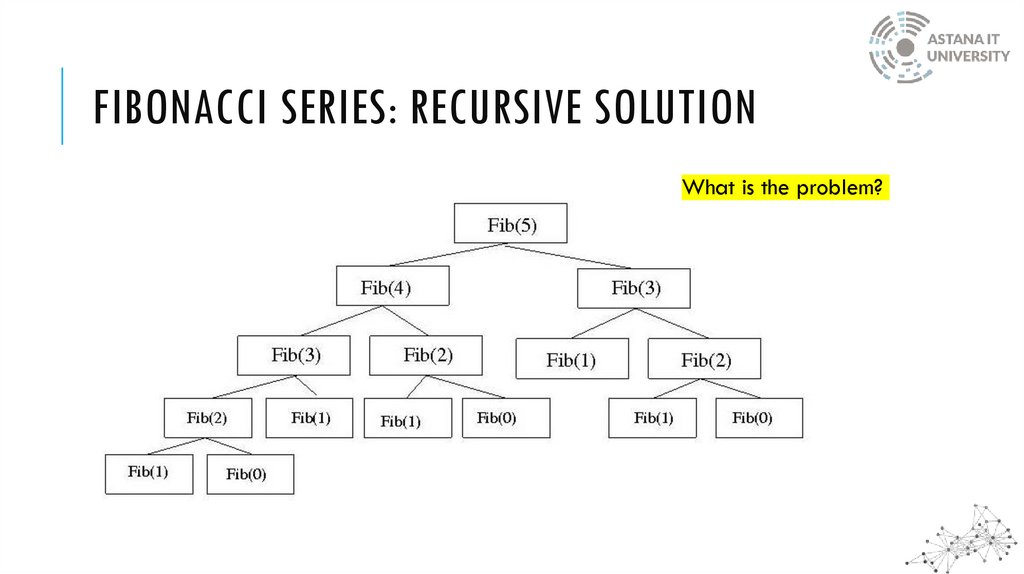
FIBONACCI SERIES: RECURSIVE SOLUTIONIt has serious issue!
6.
FIBONACCI SERIES: RECURSIVE SOLUTIONWhat is the problem?
7.
DYNAMIC PROGRAMMINGMain approach: If the same subproblem is solved several times, (ex: fib(2)
computed 3 times for finding fib(5)), we can use table to store result of a
subproblem the first time it is computed and thus never have to recompute it again.
Saving results in a table is called Memoization.
DP =
recursive solution
+
memorization or
bottom-up
8.
FIBONACCI SERIES: MEMOIZATION9.
DIVIDE-AND-CONQUER VS DP10.
DIVIDE-AND-CONQUER VS DPDivide and Conquer algorithms
Dynamic Programming
1
Split a problem into separate subproblems,
solve the subproblems, and combine the results
for a solution to the original problem
Splits a problem into subproblems, some of
which are common, solves the subproblems, and
combines the results for a solution to the original
problem.
2
Can be thought as a top-down algorithms
Can be thought as a bottom-up
3
Subproblems are independent
Subproblems are not independent
4
Simple compare to DP
Solutions can often be quite complex and tricky.
5
Can be used for any kind of problems
Generally used for Optimization problems
11.
STEPS TO DESIGN DP1.
Define subproblems
2. Recursively define the value of an optimal solution
3. Recognize and solve the base case











 Программирование
Программирование








