Миноры и алгебраические дополнения. Основное понятие минора

1. Миноры и алгебраические дополнения.

2. Основное понятие минора

Пусть
detA =
а11 а12 а13
a21 а22 а23
а31 а32 а33
тогда
Минором любого элемента этого определителя
называется определитель второго порядка, полученный
из данного вычеркиванием строки и столбца, на
пересечении которых стоит элемент.
Обозначается Мij , где i – номер строки, j – номер столбца.
М31 =
а12 а13
а22 а23
а11 а13
М32 = a21 а23
М22 =
а11 а13
а31 а33

3. Рассмотрим пример 1

Задание.
Решение.
Задан определитель А. Найти минор M23 к элементу
в заданном определителе вторую
aВычеркиваем
23 определителя
строку и третий столбец:
Тогда
detA =
ОТВЕТ:

4. Алгебраическое дополнение

Пусть задан detA =
а11 а12 а13
a21 а22 а23
а31 а32 а33
тогда
Алгебраическое дополнение элемента аij данного
определителя называют минор этого же элемента, взятый
i+j
со знаком (-1)
, где i,j –номера соответственно строки и
столбца, на пересечение которых находится элемент.
Обозначается Аij , где i – номер строки, j – номер столбца
и задаётся формулой (1)
где Мij – минор этого же элемента
А ij = ( -1)
i+j
М ij
(1)

5. Рассмотрим пример 2

Задание.
Найти алгебраическое дополнение А23 к
элементу а23
Решение.
1
Ответ:

6. Теорема о вычислении определителя

Определитель равен сумме произведений
элементов какой-либо строки (столбца) на
их алгебраические дополнения.
ТЕОРЕМА
Пусть задан
detA =
а11 а12 а13
a21 а22 а23
а31 а32 а33
, тогда
det A = a11 A11 + a12 A12 + a13 A13
( 2)
ПРИМЕЧАНИЕ
Обычно выбирают ту строку или столбец, в котором есть нули.

7.

Разложение определителя по строке
Пусть задан
detA =
а11 а12 а13
a21 а22 а23
а31 а32 а33
det A = a11 A11 + a12 A12 + a13 A13
, тогда
= а11 (-1)
а22 а23
а32 а33
1+1
А11
(2)
+ а12 (-1)
1+2
a21 а23
а31 а33
А12
+
а13 (-1)
1+3
a21 а22
а31 а32
А13
+

8.

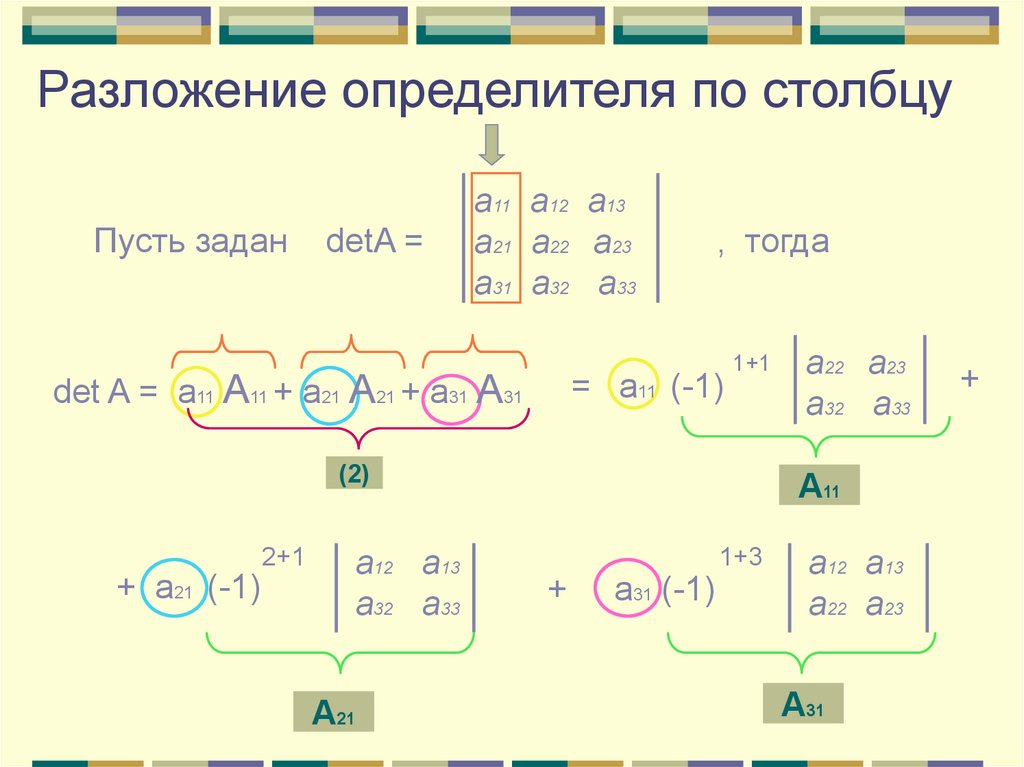
Разложение определителя по столбцу
Пусть задан
detA =
а11 а12 а13
a21 а22 а23
а31 а32 а33
, тогда
= а11 (-1)
det A = a11 A11 + a21 A21 + a31 A31
1+1
(2)
+ а21 (-1)
2+1
a12 а13
а32 а33
А21
а22 а23
а32 а33
А11
+
а31 (-1)
1+3
a12 а13
а22 а23
А31
+

9. Рассмотрим пример 3

Задание.
Вычислить определитель, разложив его по
первой строке
Решение.
Ответ:

10. Примечание

Заметим, что понятие минора применяется и по
отношению к матрице. Это определитель любой
квадратной подматрицы для данной.
Пусть дана матрица А .
А=
1 7 -1 9
0 2 3 -2
8 4 6 5
3 х4
Определителя у этой матрицы
нет, т.к. она не квадратная, но
для нее можно составить
очень много миноров
Рассмотрим их

11.

Миноры 3-го порядка матрицы А
А=
1 7 -1 9
0 2 3 -2
8 4 6 5
1
М3 =
3
М3 =
3 х4
1 7 -1
0 2 3
8 4 6
1 -1 9
0 3 -2
8 6 5
Образуются с помощью
вычеркивания любого из
столбца
2
М3 =
4
М3 =
1 7 9
0 2 -2
8 4 5
7 -1 9
2 3 -2
4 6 5

12.

Миноры 2-го порядка матрицы А
1
А=
1 7 -1 9
0 2 3 -2
8 4 6 5
М2 =
3 х4
2
1 7
0 2
3
М2 = 2 3
4 6
М2 =
1 9
8 5
Миноров 2-го порядка этой матрицы А по
количеству будет еще больше.
Миноры 1-го порядка матрицы А
2
1
А=
1 7 -1 9
0 2 3 -2
8 4 6 5
М1 =
1
=1
3
М1 =
М1 =
4
=4
5
=5
4
-2 = -2
М1 =
3 х4
Вывод. Минор – это определитель любой квадратной
подматрицы для данной.