Объединение и пересечение событий

1.

Объединение и
пересечение событий.

2. Ответьте на вопросы:

• Что такое элементарное событие?
• Что такое случайное событие?
• Что такое достоверное событие?
• Что такое невозможное событие?

3.

Напомним:
Случайный опыт (случайный эксперимент) математическая
абстракция,
описывающая
реальный опыт, который может оканчиваться
различными событиями
Случайный опыт оканчивается каким-либо одним
элементарным
событием.
Какое
именно
элементарное событие наступает в данном опыте –
дело случая. Два различных элементарных события
одновременно произойти не могут.
Случайное событие или просто событие – это
некоторое
множество
(набор,
совокупность)
элементарных событий.
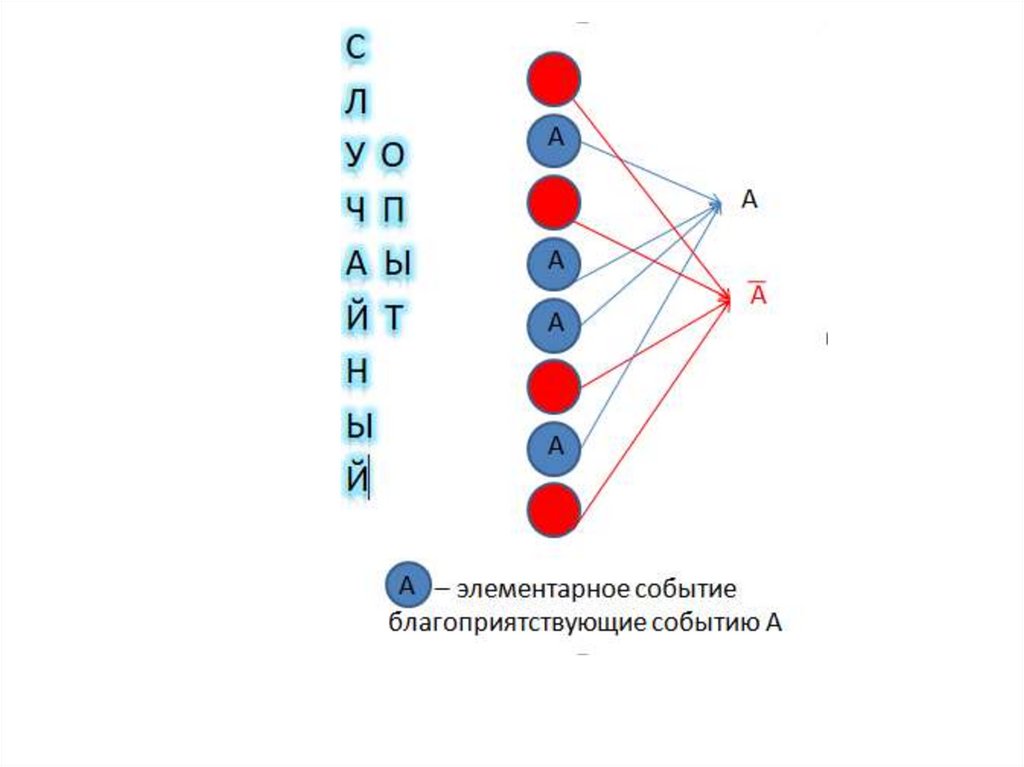
Случайное
событие
A
наступает,
когда
происходит какое - либо элементарное событие,
благоприятствующие событию A.

4.

Событием, противоположным событию
А,
называют
событие,
которому
благоприятствуют
все
элементарные
события,
не
благоприятствующие
событию А.
Обозначение:
События А и А называют взаимно
противоположными
или
дополнительными друг для друга.

5.

6. Пример

Бросают игральную кость. Рассмотрим событие А «выпало число, большее
4». Этому событию благоприятствуют элементарные события «выпала
пятёрка» и «выпала шестёрка». Не благоприятствуют событию А следующие
элементарные события: «выпала единица», «выпала двойка», «выпала
тройка», «выпала четвёрка» (см. рис.). Для события А противоположным
событием А является событие «выпало число, меньшее или равное четырём».
Событие А
Событие А
Взаимно противоположные события одновременно произойти не могут, но
какое – либо из них происходит обязательно. Поэтому
Р(А) + Р(А) = 1.
Иными словами, сумма вероятностей взаимно противоположных событий
равна единице.
Следовательно,
Р(А) = 1 – Р(А) и Р(А) = 1 – Р(А)
Из этих формул следует что для вычисления Р(А) достаточно знать Р(А)
Это свойство во многих случаях оказывается полезным.

7. Свойства противоположных событий

1) Если В = А, то А = В
2) Взаимно противоположные события одновременно произойти не
могут, но какое – либо из них происходит обязательно.
Р(А) + Р(А) = 1
3) Для вычисления Р(А) достаточно знать Р(А).
Р(А) = 1 – Р(А)
Р(А) = 1 – Р(А)

8. Диаграммы Эйлера

Соотношения
и
связи
между
событиями
можно
изобразить
с
помощью
схематических
рисунков
–
диаграмм Эйлера.
Если
нужно
изобразить
несколько событий, то рисуют
несколько фигур – по одной
для каждого события. При этом
фигуры могут располагаться по
– разному, показывая, как
связаны между собой данные
события.
Событие А
А
Событие А,
противоположное
А

9.

Упражнение 1:
В случайном эксперименте 20 элементарных событий. Событию А
благоприятствуют 12 из них. Сколько элементарных событий
благоприятствуют событию противоположному А?
Упражнение 2:
В некотором случайном опыте может произойти событие K. Найдите
вероятность события противоположного K, если вероятность события K
равна:
А) 0,4; Б) 0,85; В) 0,13; Г)
; Д) p.
Упражнение 3:
Докажите, что события A и B не могут быть противоположны, если P(A) =
0,7, а P(B)= 0,44.

10.

Операции над множествами:
А = {4, 5, 6, 7}, B = {6, 7, 8, 9, 10, 11}
Пересечение множеств:
A B 6, 7
Объединение множеств:
A B 4, 5, 6, 7, 8, 9, 10, 11

11.

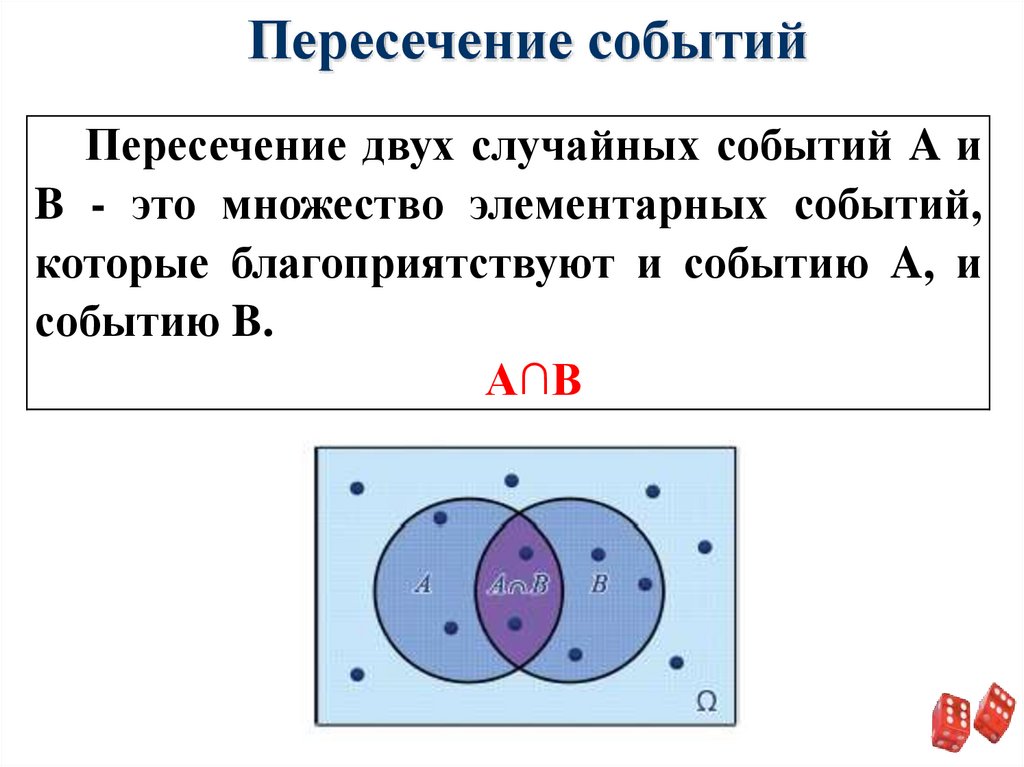
Пересечение событий
Пересечение двух случайных событий A и
B - это множество элементарных событий,
которые благоприятствуют и событию A, и
событию B.
A∩B

12.

Пересечение событий
Пересечением событий А и В
называется событие С, которое
происходит тогда и только тогда,
когда происходят одновременно оба
события А и В
C A B

13.

Объединение событий
Объединение двух случайных событий A и
B - это множество элементарных событий,
которые благоприятствуют хотя бы одному из
событий A и B.
AUB

14.

Объединение событий
Объединением событий А и В
называется событие С, которое
происходит тогда и только тогда,
когда происходит хотя бы одно из
двух событий А или В
C A B

15.

№1. Продавец выбирает два костюма, для того чтобы
поместить их в витрину магазина. В ассортименте
есть черные (Ч) и синие (С) костюмы.
Элементарные события этого случайного опыта
представляют собой пары костюмов:
ЧС, ЧЧ, СС,СЧ.
Событие А: первый костюм черного цвета.
А: ЧС, ЧЧ.
Событие Б: второй костюм черного цвета.
Б: ЧЧ, СЧ.
А В «хотя бы один из костюмов черного цвета».
А В ЧС,ЧЧ , СЧ
А В «оба костюма черные»
А В ЧЧ

16.

Несовместные события
Событий А и В называются
несовместными, если они не имеют
общих благоприятствующих
элементарных события, т.е. они не
могут наступить одновременно в
одном и том же опыте

17.

Несовместные события
Пересечение несовместных событий А и В
является пустое множество
A B
Событие А: выпала тройка
Событие В: выпала пятерка

18.

Х Х Х Х
Х Х
Х Х
Событие А В : «хотя бы раз выпало
меньше, чем три очка»
Х Х Х
Х Х Х
Х Х Х Х
Событие А В: «оба раза выпало
меньше трех очков»
Х Х
Х Х Х Х
Х Х
Х Х
Х Х Х
Х Х
Х Х
Х Х
Х
Х
Х Х
Х Х Х

19. Решить: