Эти известные, неизвестные функции…

1.

Учитель математики
ГБОУ гимназия №74
Карасева Марина Викторовна

2.

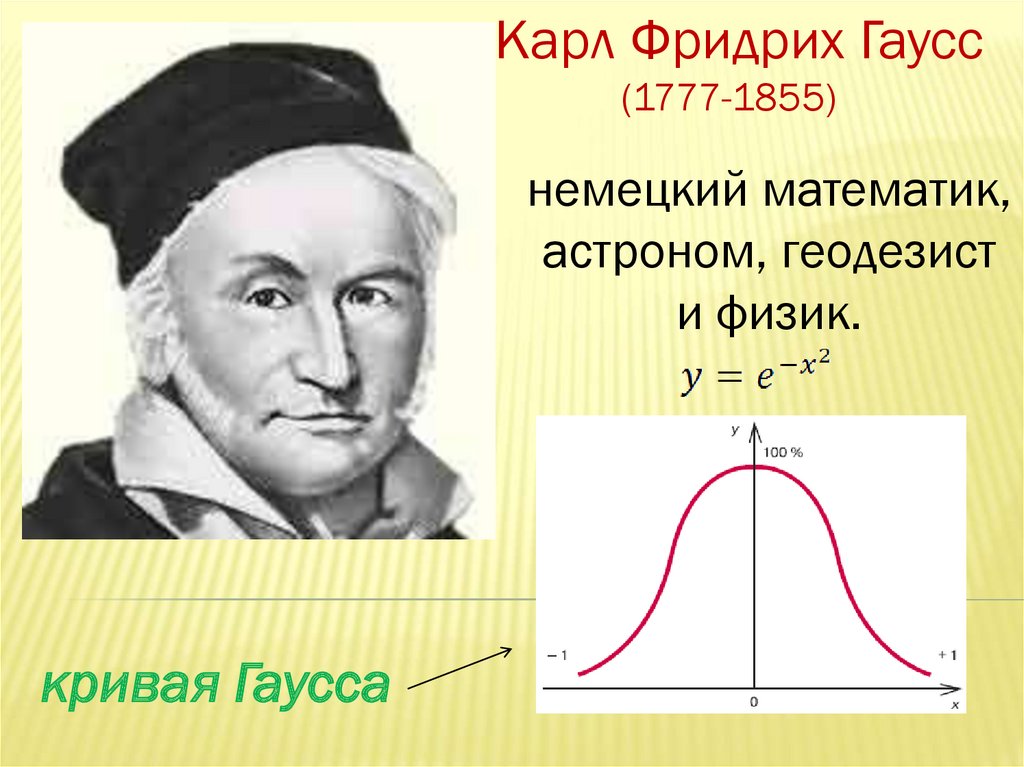
Карл Фридрих Гаусс
(1777-1855)
немецкий математик,
астроном, геодезист
и физик.
кривая Гаусса

3.

Гиперболические функции задаются
следующими формулами
гиперболический синус:
shx =
гиперболический косинус:
chx =
гиперболический тангенс:
thx =
гиперболический котангенс:
cthx =

4.

ГИПЕРБОЛИЧЕСКИЙ СИНУС
shx =
D(y) = R
E(y) =R
Найдем производную функции
y = shx
y` = chx =
При любом значении х Y`(x) >0
=> Функция y = shx
возрастает на всей числовой оси!
и не имеет точек экстремума
X=0 ; Y=0

5.

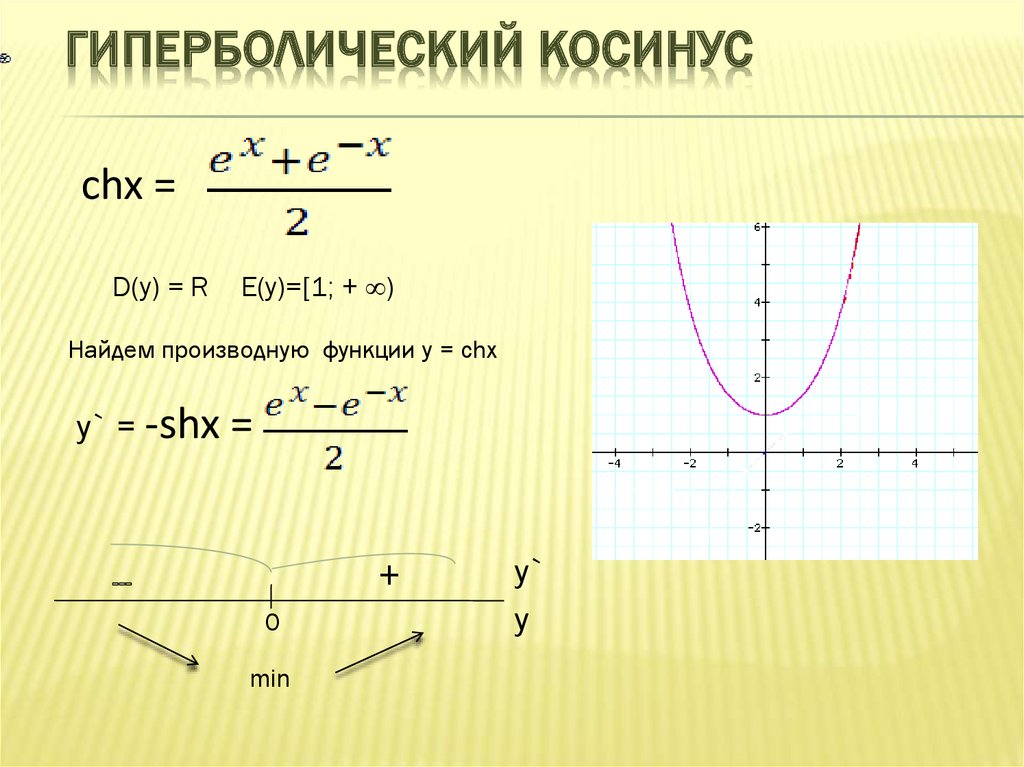
ГИПЕРБОЛИЧЕСКИЙ КОСИНУС
chx =
D(y) = R
Е(y)=[1; + ∞)
Найдем производную функции y = сhx
y` = -shx
=
+
---
0
min
y`
y

6.

ГИПЕРБОЛИЧЕСКИЙ ТАНГЕНС
thx =
D(y) = R
E(y) =R
Найдем производную функции y = thx
y` =
Функция возрастает на (-∞; +∞)

7.

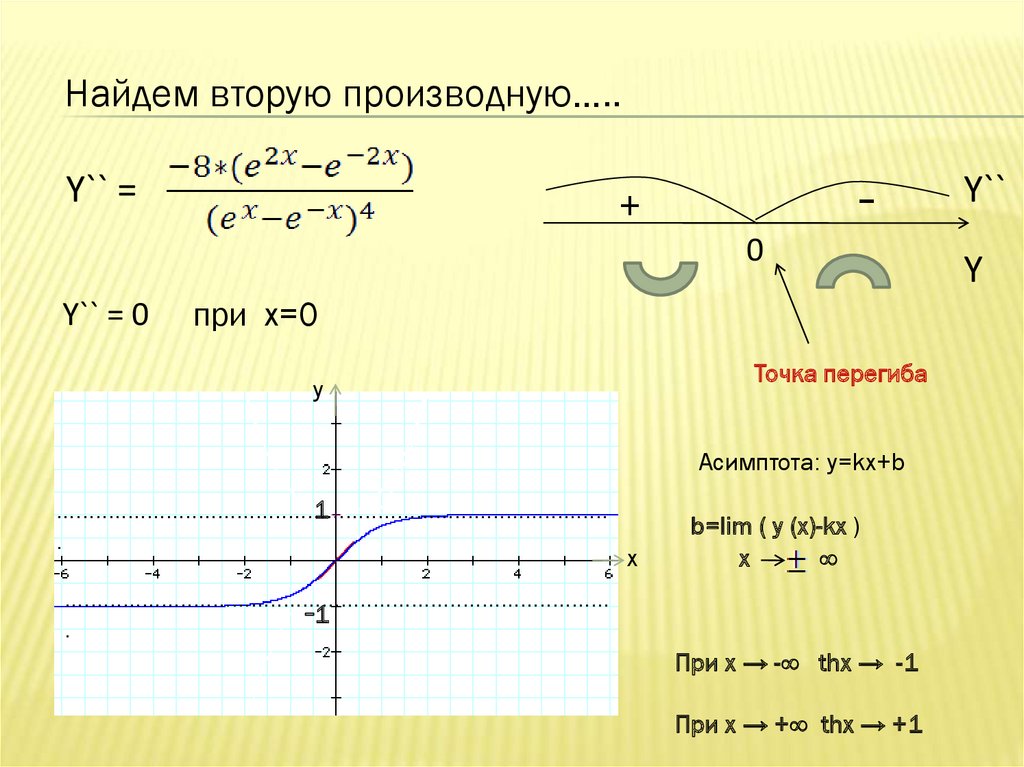
Найдем вторую производную…..
Y`` =
-
+
0
Y`` = 0
при x=0
Точка перегиба
y
Асимптота: y=kx+b
…...................................................................................
1
.
x
b=lim ( y (x)-kx )
x
∞
…..................................................................................
-1
.
При x → -∞ thx → -1
При x → +∞ thx → +1
Y``
Y

8.

ГИПЕРБОЛИЧЕСКИЙ КОТАНГЕНС
D(y) = R\{0}
y` =
-
E(y) =(-∞; -1)
∩
cthx =
При любом значении х y`(x) < 0
=> Функция y = cthx
Убывает на всей числовой оси!
и не имеет точек экстремума
(1;+∞)

9.

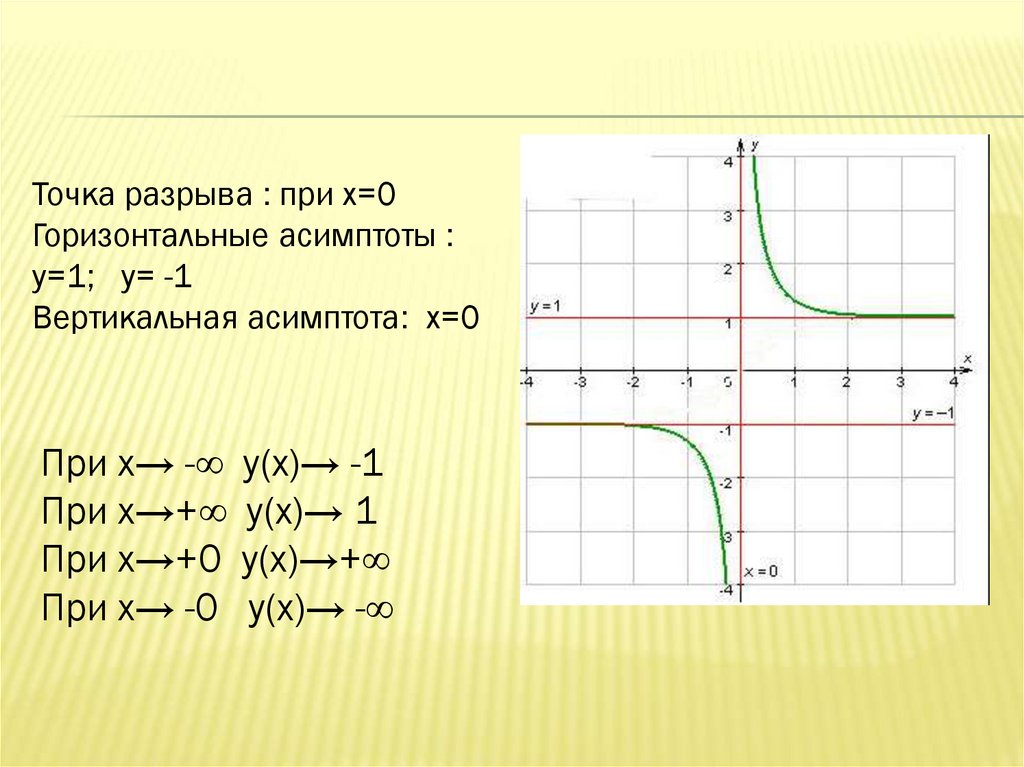
Точка разрыва : при х=0
Горизонтальные асимптоты :
y=1; y= -1
Вертикальная асимптота: x=0
При x→ -∞
При x→+∞
При x→+0
При x→ -0
y(x)→ -1
y(x)→ 1
y(x)→+∞
y(x)→ -∞