Похожие презентации:
Графики основных элементарных функций
1. Лекция 1.2.
• Графики основных элементарных функций• Числовая последовательность.
• Предел числовой последовательности.
• Единственность предела.
• Ограниченность сходящейся числовой
последовательности.
1
2.
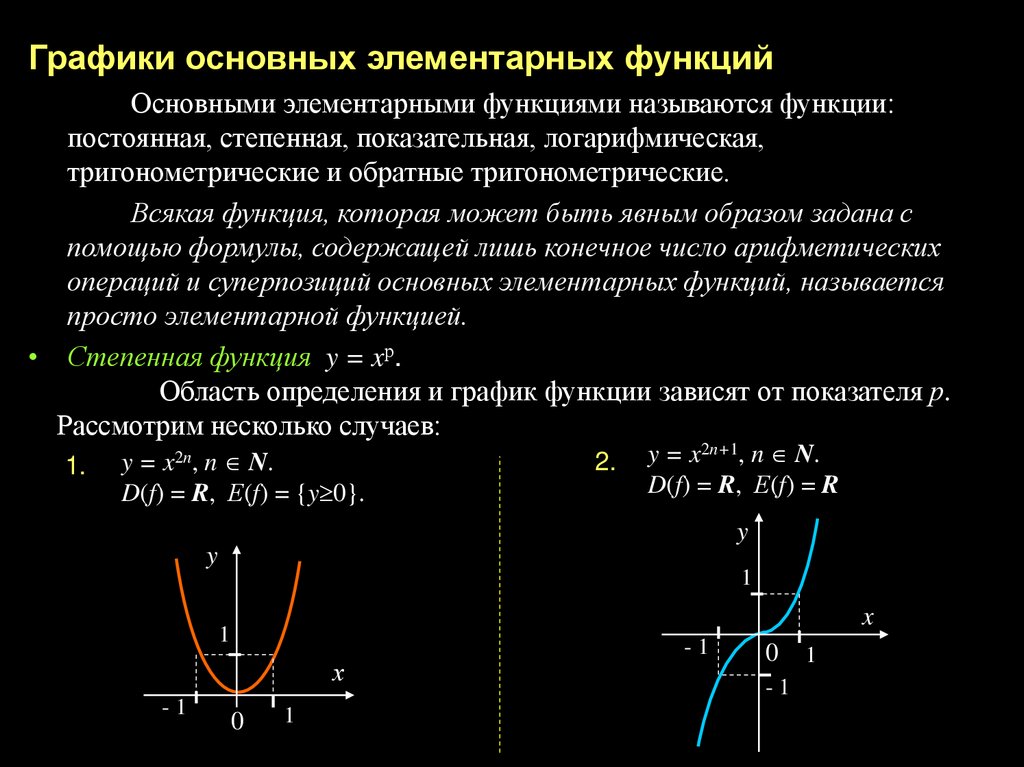
Графики основных элементарных функцийОсновными элементарными функциями называются функции:
постоянная, степенная, показательная, логарифмическая,
тригонометрические и обратные тригонометрические.
Всякая функция, которая может быть явным образом задана с
помощью формулы, содержащей лишь конечное число арифметических
операций и суперпозиций основных элементарных функций, называется
просто элементарной функцией.
• Степенная функция y = xр.
Область определения и график функции зависят от показателя р.
Рассмотрим несколько случаев:
1.
y = x2n, n N.
D(f) = R, Е(f) = {y 0}.
2.
y = x2n+1, n N.
D(f) = R, Е(f) = R
y
y
1
x
1
х
-1
0
1
-1
0
1
-1
2
3.
• .3. y 2 n x ,
n N
D( f ) {x 0),
4.
E ( f ) { y 0}
y 2 n 1 x ,
n N
D ( f ) R,
E( f ) R
y
y
1
x
1
-1
x
0
0
1
-1
1
1
, n N
5.
x 2n
D( f ) {x 0},
y
6.
E ( f ) { y 0}
y
1
, n N
x 2 n 1
D( f ) {x 0},
E ( f ) { y 0}
y
1
y
x
-1
1
0
1
-1
x
-1
0
1
3
4.
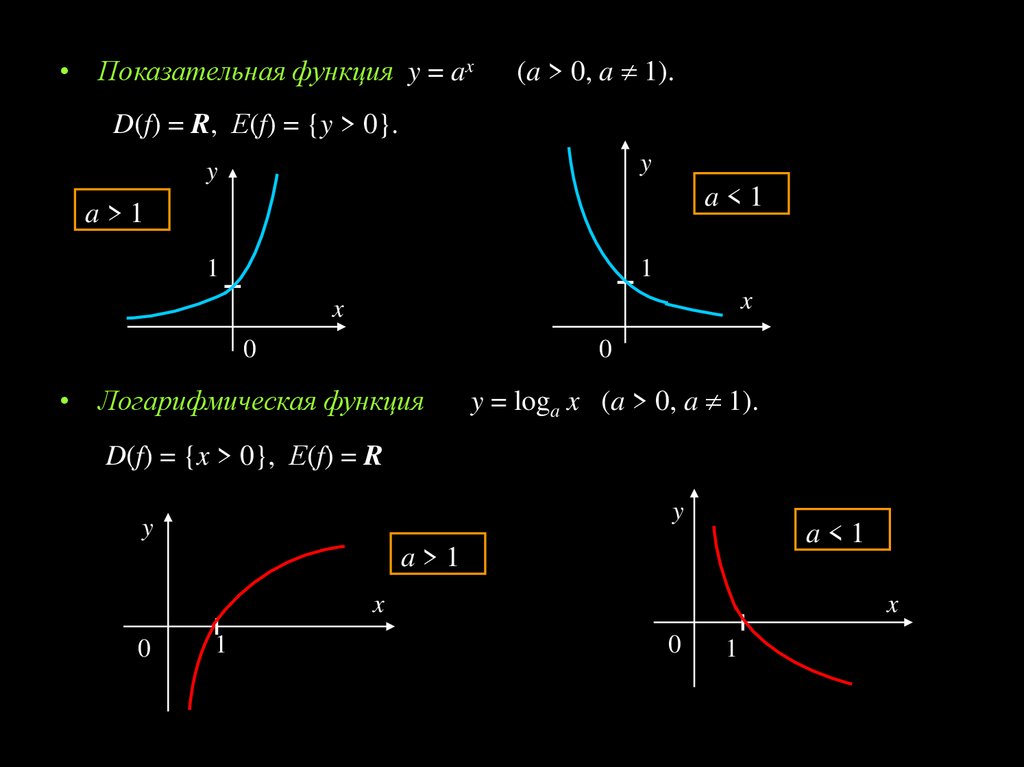
• Показательная функция y = ax(a > 0, a 1).
D(f) = R, Е(f) = {y > 0}.
y
y
a<1
a>1
1
1
x
x
0
0
• Логарифмическая функция
y = loga x (a > 0, a 1).
D(f) = {x > 0}, Е(f) = R
y
y
a<1
a>1
x
0
1
x
0
1
4
5.
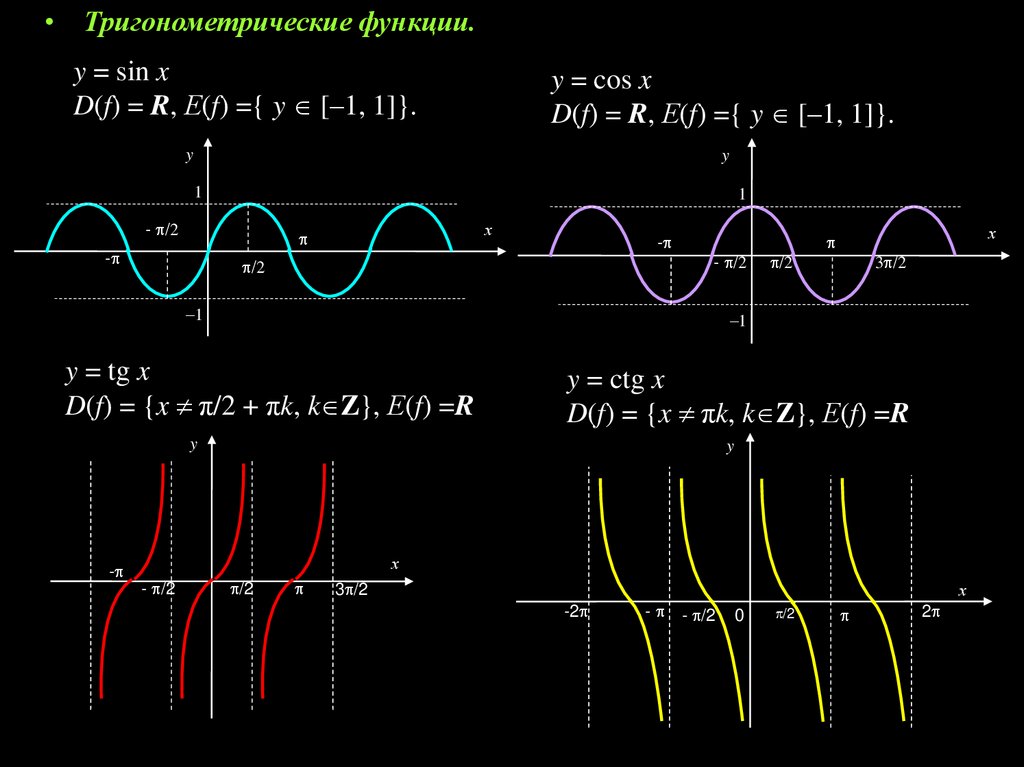
• Тригонометрические функции.y = sin x
D(f) = R, Е(f) ={ y [–1, 1]}.
y = cos x
D(f) = R, Е(f) ={ y [–1, 1]}.
y
y
1
1
- /2
х
-
-
/2
- /2
–1
3 /2
–1
y = tg x
D(f) = {x π/2 + πk, k Z}, Е(f) =R
y = ctg x
D(f) = {x πk, k Z}, Е(f) =R
y
-
/2
х
y
х
- /2
/2
х
3 /2
-2
- - /2
0
/2
2
5
6.
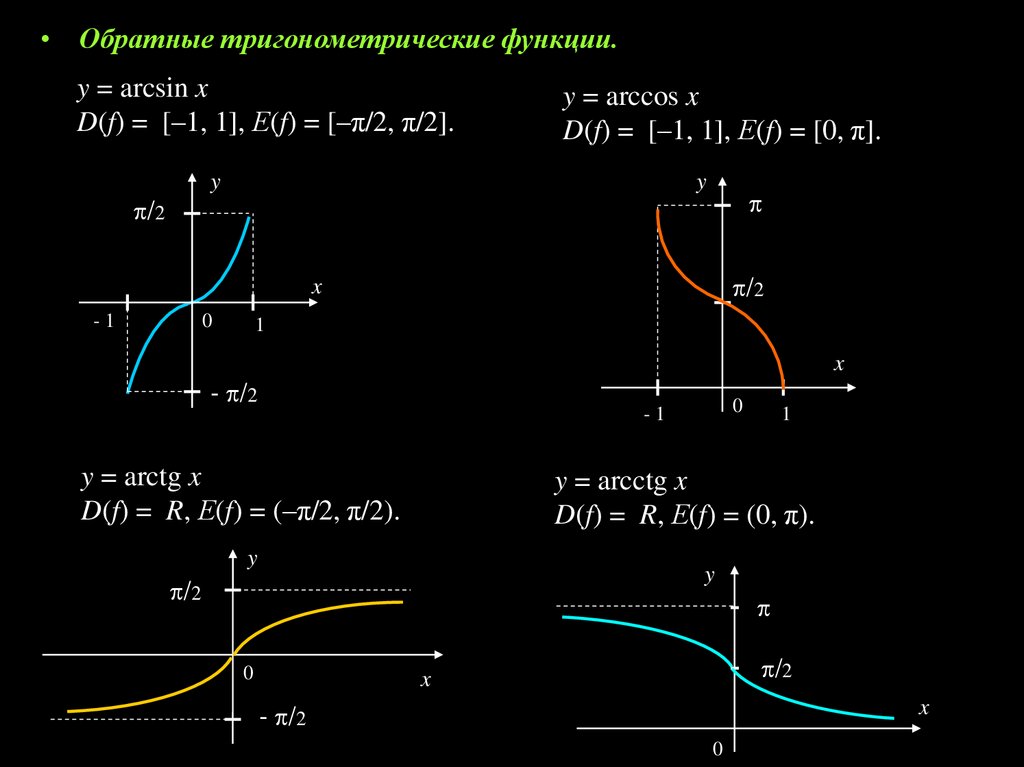
• Обратные тригонометрические функции.y = arcsin x
D(f) = [–1, 1], Е(f) = [–π/2, π/2].
y = arccos x
D(f) = [–1, 1], Е(f) = [0, π].
y
y
/2
/2
x
-1
0
1
x
- /2
0
-1
y = arctg x
D(f) = R, Е(f) = (–π/2, π/2).
1
y = arcctg x
D(f) = R, Е(f) = (0, π).
y
y
/2
0
/2
x
x
- /2
0
6
7.
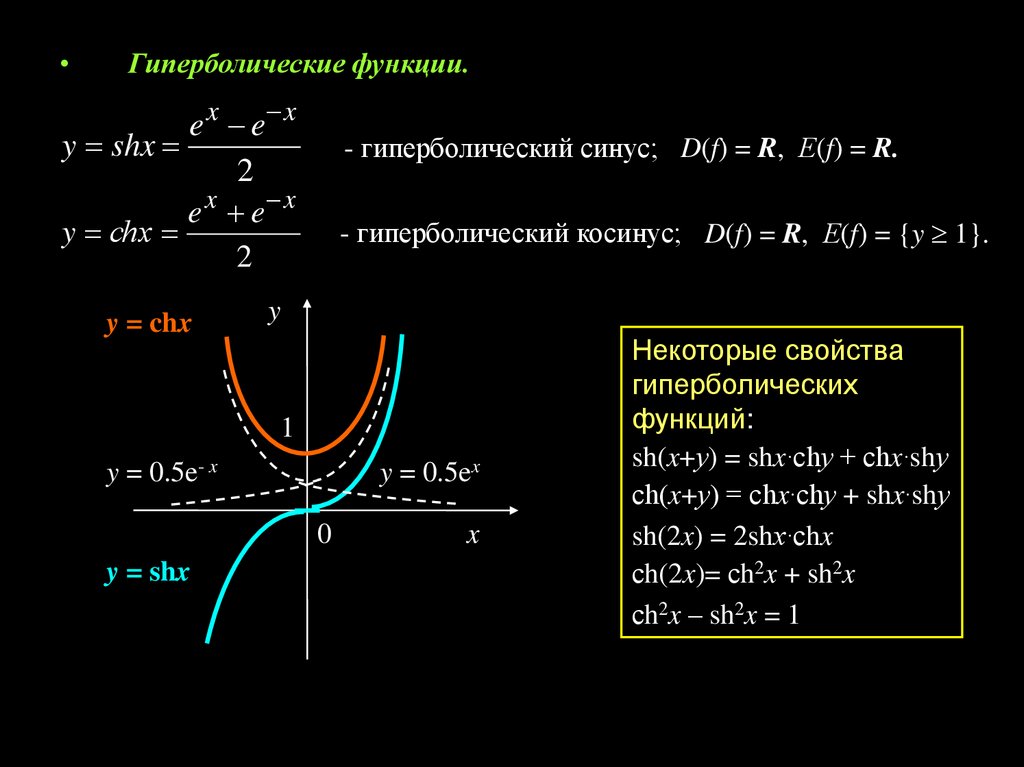
Гиперболические функции.
e x e x
y shx
2
e x e x
y сhx
2
y = chx
- гиперболический синус; D(f) = R, Е(f) = R.
- гиперболический косинус; D(f) = R, Е(f) = {y 1}.
y
1
y = 0.5e- x
y = 0.5ex
0
y = shx
x
Некоторые свойства
гиперболических
функций:
sh(x+у) = shx·сhу + сhx·shу
сh(x+у) = сhx·сhу + shx·shу
sh(2x) = 2shx·сhx
сh(2x)= сh2x + sh2x
сh2x – sh2x = 1
7
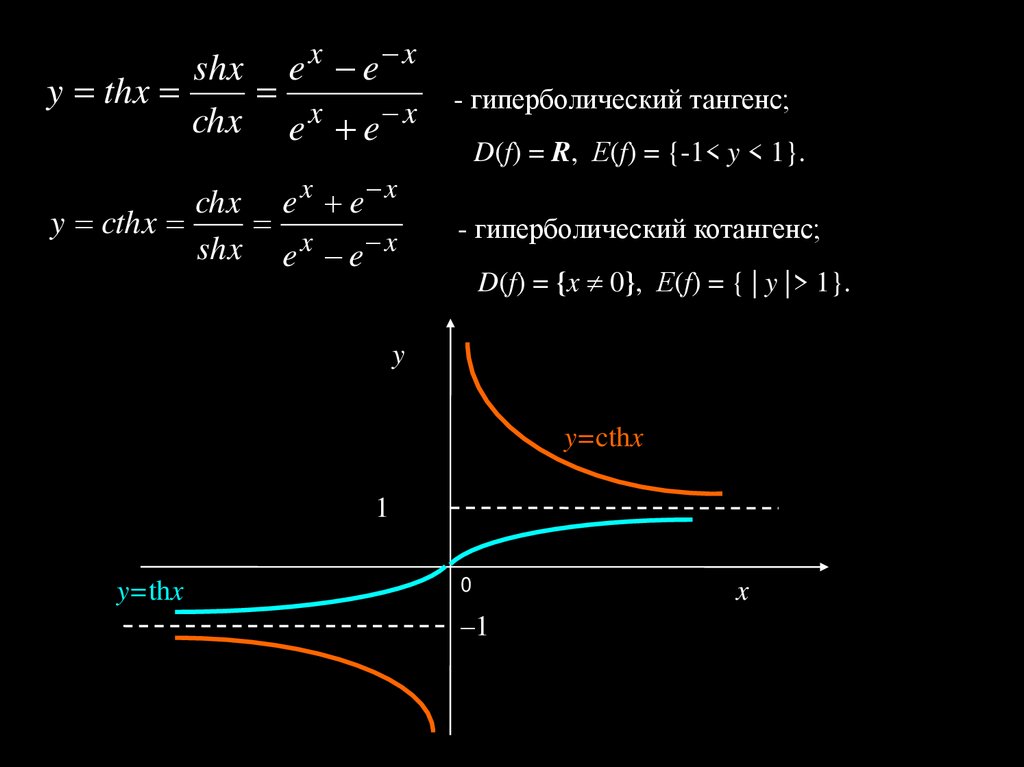
8.
shx e x e xy thx
chx e x e x
- гиперболический тангенс;
chx e x e x
y cthx
shx e x e x
- гиперболический котангенс;
D(f) = R, Е(f) = {-1< y < 1}.
D(f) = {x 0}, Е(f) = { | y |> 1}.
y
y=cthx
1
y=thx
0
x
–1
8
9. Понятие числовой последовательности.
Если каждому числу n N поставлено в соответствие определённоечисло хn R, то полученное упорядоченное множество
х1, х2, … , хn , …
называют числовой последовательностью (ЧП).
Таким образом, числовая последовательность – это
функция, областью определения которой является все
множество натуральных чисел N. Значения этой функции хn
называются элементами последовательности, число n называется
номером элемента.
Кратко числовую последовательность обозначают
или {хn} .
xn n 1
Числовая последовательность может быть задана с помощью
формулы,
позволяющей
вычислить
каждый
элемент
последовательности по его номеру.
9
10. Примеры.
1)1, 1, 1, …
хn=1, n N ;
2)
–1, 1, –1, 1, …
хn= (–1)n , n N ;
3)
2,
2 2 ,
2 2 2 ,
х1 2 , xn 2 xn 1 ,
...
n 2, 3,
...
10
11. Арифметическая и и геометрическая прогрессии
xn 1 4(n 1),n
xn 5 2
n 1
,
n
11
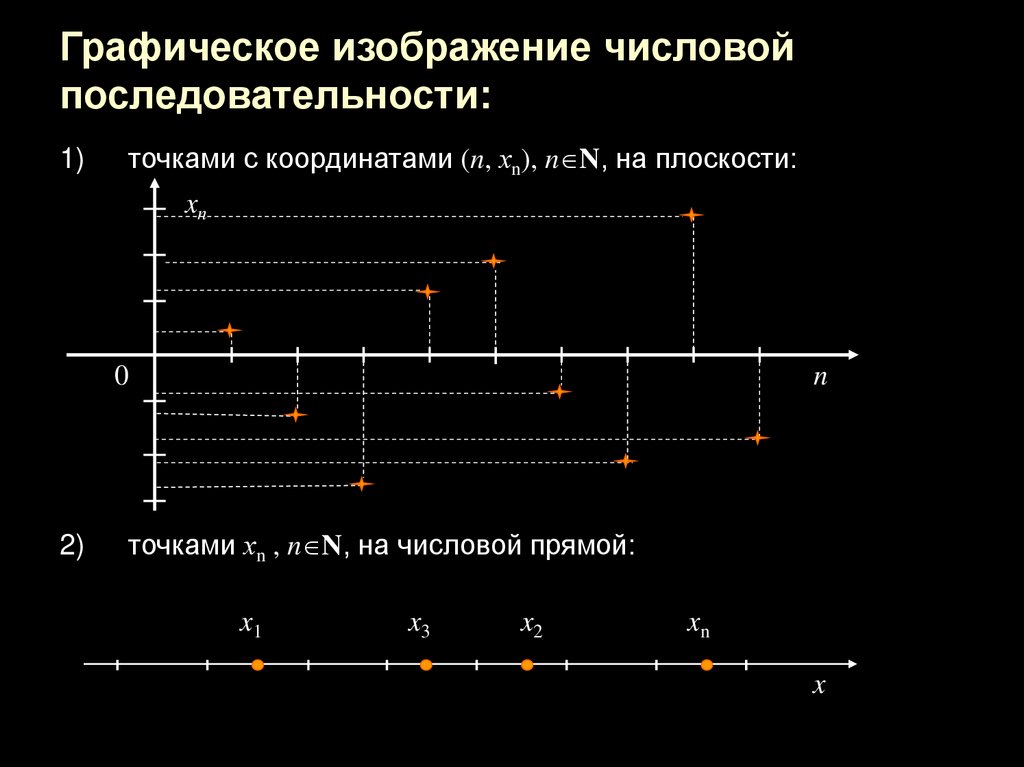
12. Графическое изображение числовой последовательности:
1)точками с координатами (n, хn), n N, на плоскости:
xn
0
2)
n
точками хn , n N, на числовой прямой:
x1
x3
x2
xn
x
12
13. Определение предела последовательности
Число a R называется пределом (числовой) последовательности {хn},если для любого числа > 0 найдется такой номер N( ) (зависящий от ),
что для всех ее элементов с номерами n N( ) выполняется неравенство
хn – a < .
В этом случае пишут
Или по-другому:
lim xn a.
n
хn a при n .
Если последовательность имеет предел, то говорят, что она сходится, в
противном случае говорят, что она расходится.
С помощью логических символов определение предела
последовательности можно записать так:
lim xn a 0 N ( ) : n N ( ) xn a
n
13
14. Геометрический вариант определения предела.
Неравенство хn – a < в определении предела эквивалентнонеравенствам
a – < xn < a + .
Другими словами, для любого числа > 0 найдется такой номер N( ),
начиная с которого, все члены ЧП принадлежат -окрестности точки a.
Число a является пределом ЧП {хn}, если в
любой его окрестности содержатся почти все
элементы последовательности, за исключением их
конечного числа.
Таким образом, вне любой -окрестности точки a лежит
лишь конечное число элементов ЧП.
14
15. Единственность предела
ТЕОРЕМА.Числовая последовательность может иметь лишь один предел.
Доказательство.
Предположим, что {хn} имеет два предела, причем а < b. Выберем
ε>0 так, чтобы ε-окрестности точек а и b не пересекались:
U (a)
U (b)
x
a
b
Так как а - предел {хn}, то вне U (a) может лежать лишь конечное
число элементов ЧП, в частности, интервал U (b) может содержать лишь
конечное число элементов последовательности. Это противоречит тому,
что b – ее предел. Полученное противоречие говорит о том, что числовая
последовательность может иметь только один предел.
15
16. Ограниченность сходящейся ЧП.
ЧП называется ограниченной, если множество ее значенийограничено сверху и снизу, т.е.
С1 R и С2 R: n N С1 xn С2.
ЧП называется неограниченной, если
С > 0 n N: хn > C.
Примеры.
xn
xn = (–1)n – ограниченная ЧП;
xn = n((–1)n+1 + 1) – неограниченная ЧП.
0
n
16
17.
ТЕОРЕМА.Если числовая последовательность имеет предел, то она ограничена.
Доказательство.
Пусть
lim xn a.
n
Возьмем = 1. Согласно определению предела числовой
последовательности, найдется такое N(1), что для всех n N(1)
выполняется неравенство
а –1 < xn < а +1.
Пусть
С1= min{x1, x2, … , xN-1, a –1},
C2= max{x1, x2, … , xN-1, a +1}.
Тогда для всех n справедливо неравенство
С1 xn C2 ,
ч.т.д.
17
18.
ЛЛЕММА.
Если хn а при n , а 0 и хn 0 для n, то числовая
.
последовательность {1/хn} ограничена
Доказательство.
Так как а 0, то = а /2 > 0. По определению предела для
данного найдется N( ) N: n N( )
хn– а < а /2.
Воспользуемся свойством модуля вещественного числа:
хn – а < хn– а < а /2
а /2 < хn < 3 а /2
1/ хn < 2/ а n N( а /2 ).
Пусть
1 1
1
2
C max ,
,...,
, .
x N 1 a
x1 x2
Тогда для всех n справедливо неравенство
1/хn С,
ч.т.д.
18












 Математика
Математика








