Похожие презентации:
Стереометрия. Векторно-координатный метод в решении задач
1. Стереометрия
Векторно- координатныйметод в решении задач
2.
Угол между прямымиа
р
q
b
р
q
cos =
р
- направляющий вектор прямой а
q
- направляющий вектор прямой b
- угол между прямыми
p x1 ; y1 ; z1
q x2 ; y2 ; z2
| x1 x2 + y1 y2 + z1 z 2 |
x12 + y12 + z12 x22 + y22 + z 22
3.
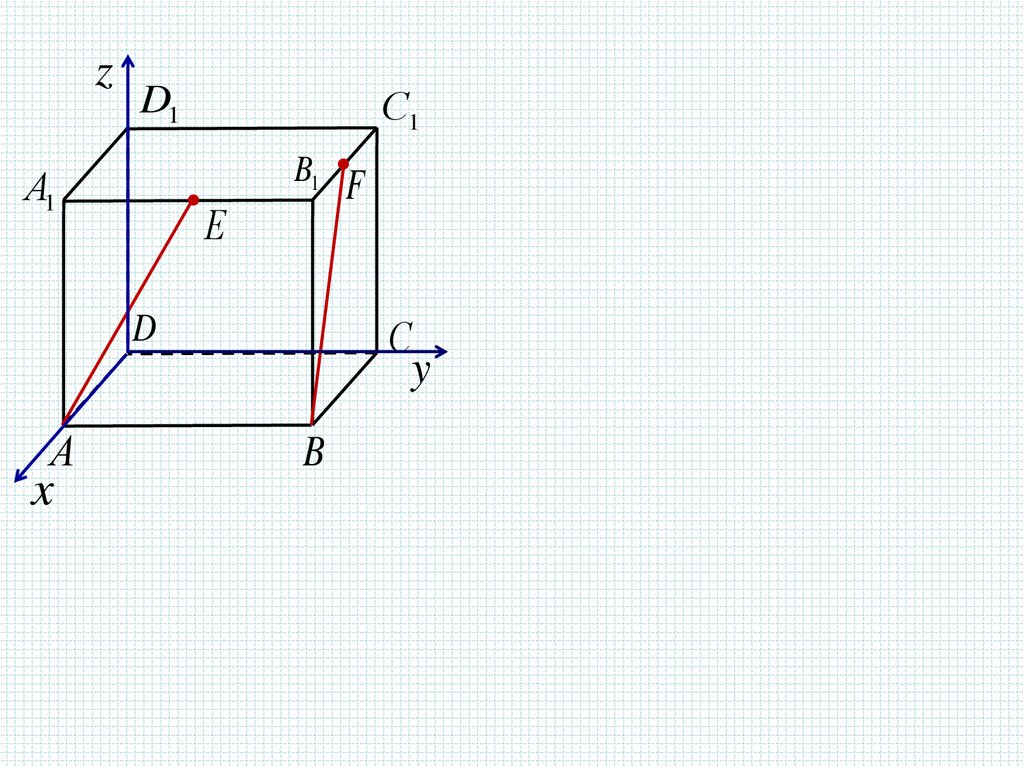
Задача 1. В единичном кубе A...D1 найдите уголмежду прямыми AE и BF, где Е – середина
ребра А1В1 , а F – середина ребра B1С1
4.
zС1
D1
А1
Е
B1 F
С
D
y
А
x
B
5.
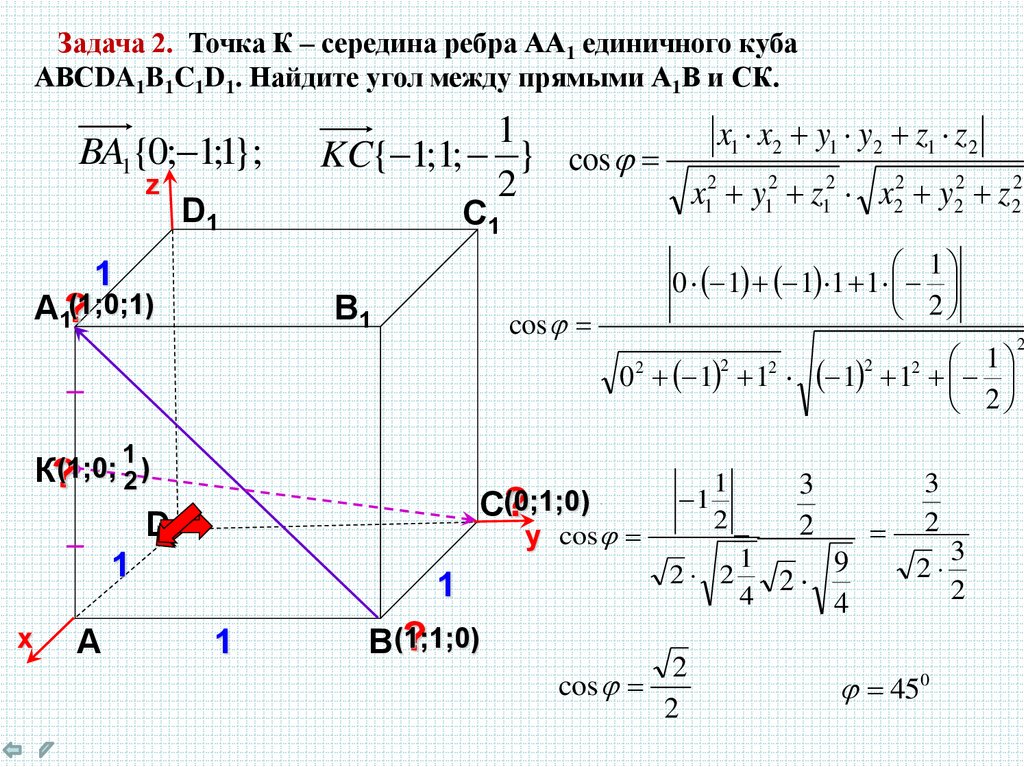
Задача 2. Точка К – середина ребра АА1 единичного кубаАВСDA1B1C1D1. Найдите угол между прямыми А1В и СК.
BA1{0; 1;1};
z
D1
1
(1;0;1)
А1?
1
x1 x2 y1 y2 z1 z2
KC{ 1;1; } cos
2
x12 y12 z12 x22 y22 z22
С1
В1
cos
1
0 1 1 1 1
2
1
2
2
0 2 1 12 1 12
2
1
(1;0; 2 )
К?
С(?0;1;0)
D
cos
1
х
А
1
1
?
В(1;1;0)
1
1
2
3
2
1
9
2 2
2
4
4
2
cos
2
3
2
2
450
3
2
2
6.
Задача 3 В правильной треугольной призме ABCA1B1C1все ребра которой равны 1, найдите косинус угла
между прямыми AD и CE, где D и E - соответственно
середины реберA1C1 иB1C1
Решение.
С1
E
D
А1
B1
С
А
B
7.
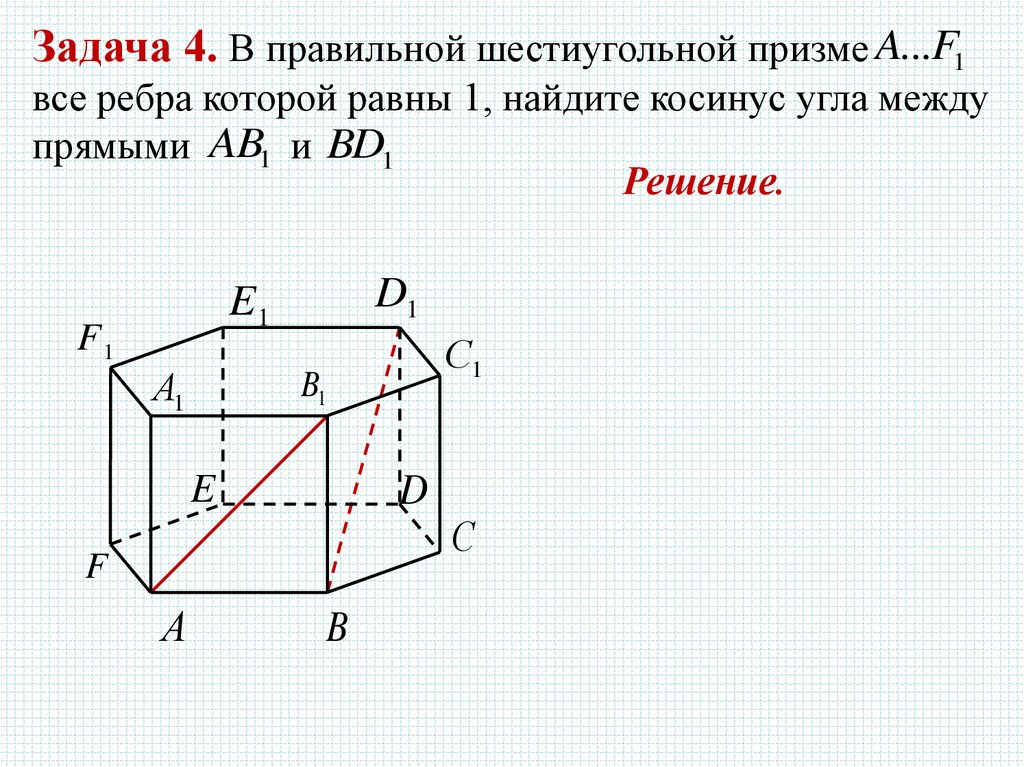
Задача 4. В правильной шестиугольной призме A...F1все ребра которой равны 1, найдите косинус угла между
прямыми AB1 и BD1
Решение.
F1
D1
E1
А1
B1
E
D
F
А
С1
B
С
8.
Задача 5. В правильной четырехугольной пирамидеSABCD, все ребра которой равны 1, отмечены точки Е и
F – середины сторон SB и SC соответственно. Найдите
угол между прямыми AE и BF.
Решение.
S
F
E
D
С
О
А
В
9.
Угол между прямой и плоскостьюр х1; у1; z1 - направляющий вектор прямой
n x2 ; у2 ; z2 - нормальный вектор плоскости
а
n
n
р
sin
| x1 x2 y1 y2 z1 z 2 |
x y z x y z
2
1
2
1
2
1
2
2
2
2
2
2
10.
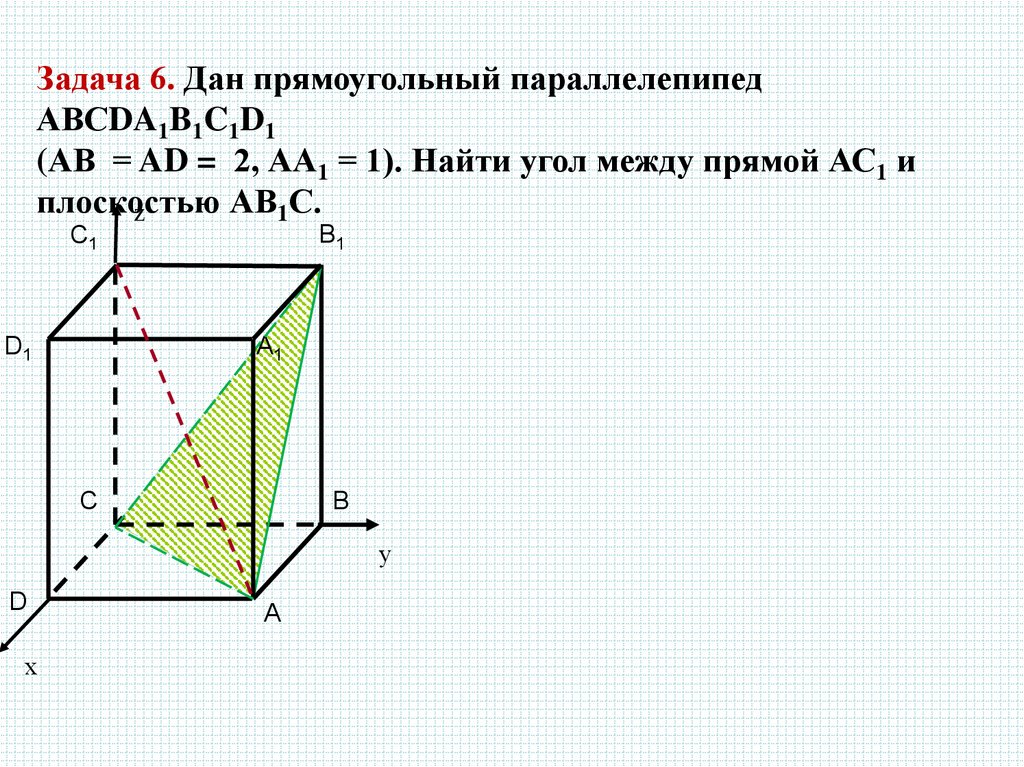
Задача 6. Дан прямоугольный параллелепипедАВСDA1B1C1D1
(АВ = AD = 2, АА1 = 1). Найти угол между прямой АС1 и
плоскостью
АВ1С.
z
B1
C1
D1
A1
C
B
у
D
х
A
11.
Задача 7. В правильной четырехугольной пирамидеSABCD , все ребра которой равны 1, найдите угол
между прямой DE, где Е- середина апофемы SF грани
ASB и плоскостью ASC
Решение.
z
S(0;0;
2
)
2
1
4
Е(0; ;
С
О
1
2
1
2
D( ; ;0)
x
2
) 1 1
4 В( ; ;0)
2 2
1
F(0; ;0)
2
А
y
12.
Уравнение плоскости, проходящей черезданную точку перпендикулярно данному
вектору
n{a; b; c}
А( x0 ; у0 ; z0 )
В( x; y; z )
n
n{a; b; c}-нормальный
вектор плоскости
А( x0 ; у0 ; z0 )
В( x; y; z )
АB x x0 ; y y0 ; z z0
n АB 0
a( x x0 ) b( y y 0 ) c( z z0 ) 0
ax by cz d 0
, где
d (ax0 by0 cz0 )
13.
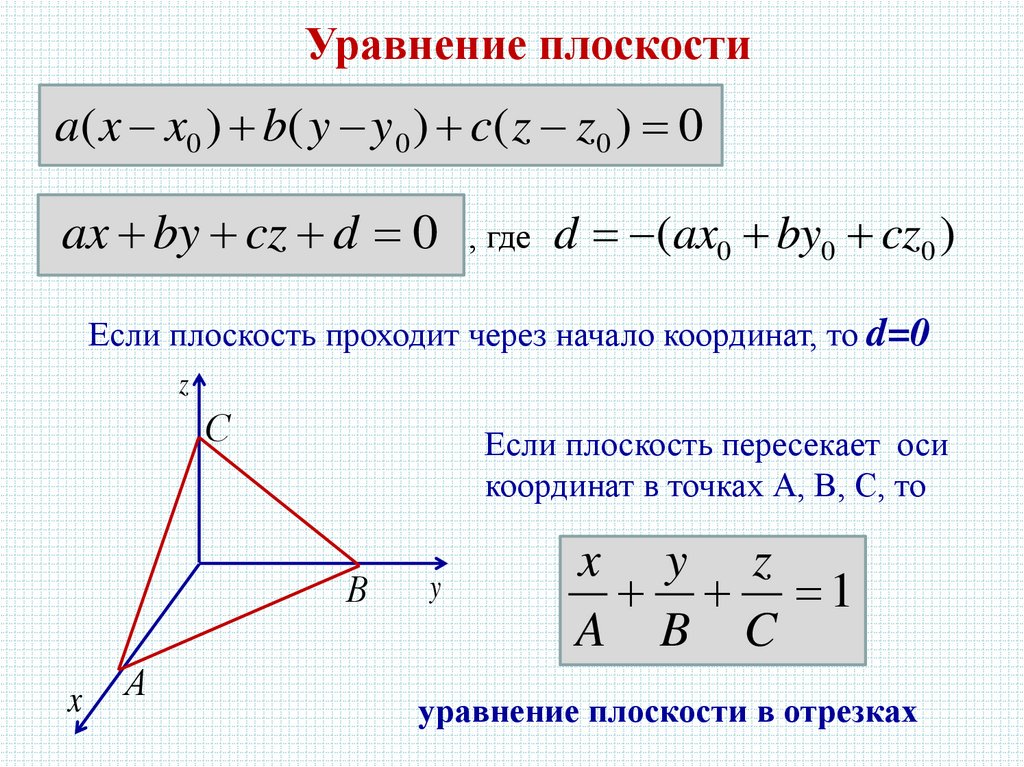
Уравнение плоскостиa( x x0 ) b( y y 0 ) c( z z0 ) 0
ax by cz d 0
, где
d (ax0 by0 cz0 )
Если плоскость проходит через начало координат, то d=0
z
С
Если плоскость пересекает оси
координат в точках А, В, С, то
В
x
А
y
x y z
1
A B C
уравнение плоскости в отрезках
14.
Задача 8. Составить уравнение плоскости,проходящей через точки А(-2;3;5), В(4;-3;0), С(0;6;-5)
и найти координаты вектора нормали.
Решение.
ax by cz d 0
2a 3b 5c d 0
4a 3b d 0
6b 5c d 0
d 5c 6b
2a 3b 10c 0
4a 9b 5c 0
5
5
a c, b c, d 5c
2
3
5
5
cx cy cz 5c 0
2
3
15 x 10 y 6 z 30 0
n{15;10;6}
15.
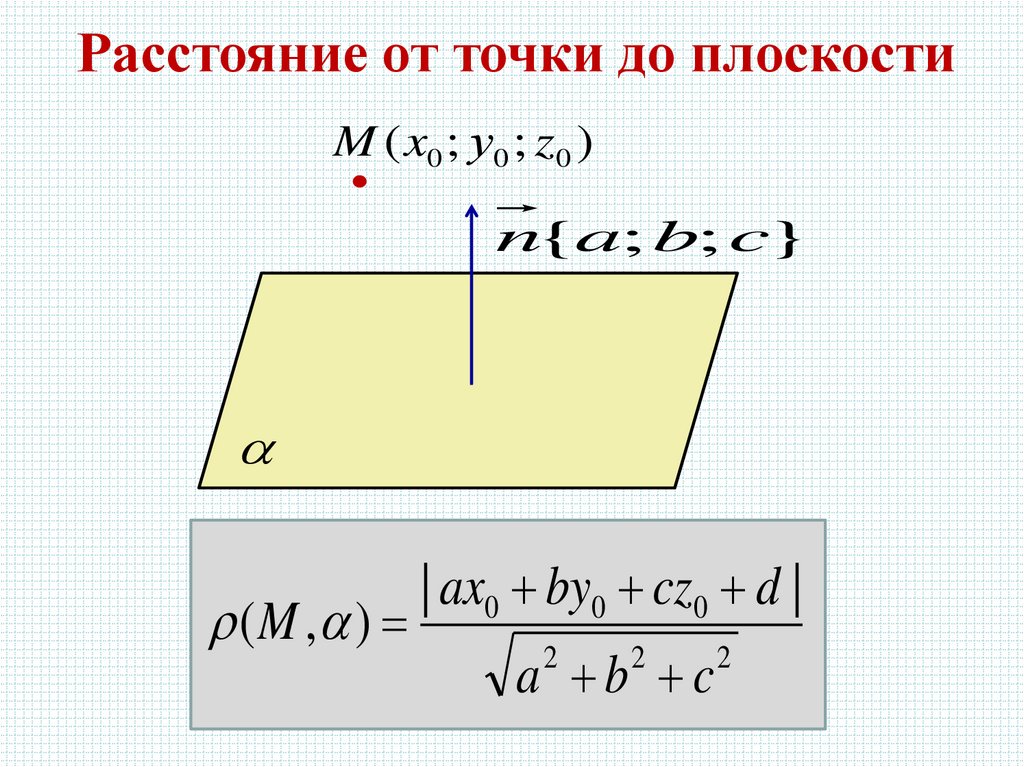
Расстояние от точки до плоскостиM ( x0 ; у0 ; z0 )
n{a; b; c}
(M , )
| ax0 by0 cz0 d |
a b c
2
2
2
16.
Расстояние междупараллельными плоскостями
ax by cz d1 0
ax by cz d2 0
( , )
| d 2 d1 |
a b c
2
2
2
17.
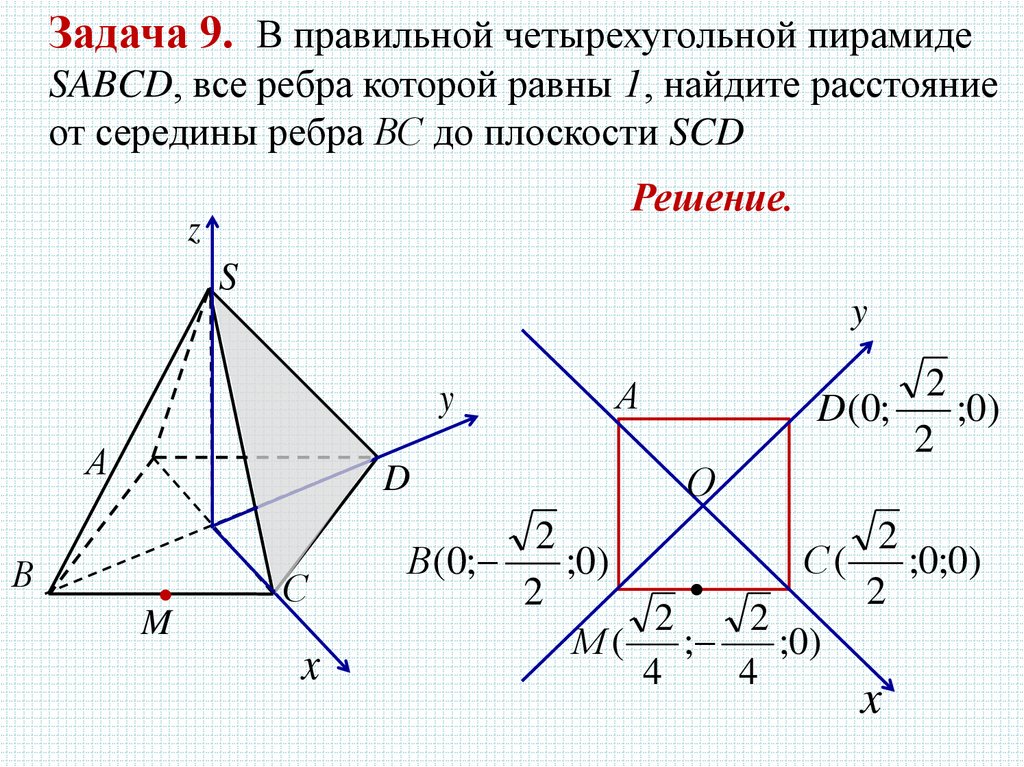
Задача 9. В правильной четырехугольной пирамидеSABCD, все ребра которой равны 1, найдите расстояние
от середины ребра ВС до плоскости SCD
Решение.
z
S
y
y
А
D
В
M
С
x
А
О
2
D (0;
;0)
2
2
2
С(
;0;0)
В (0;
;0)
2
2
2
2
М(
;
;0)
4
4
x
18.
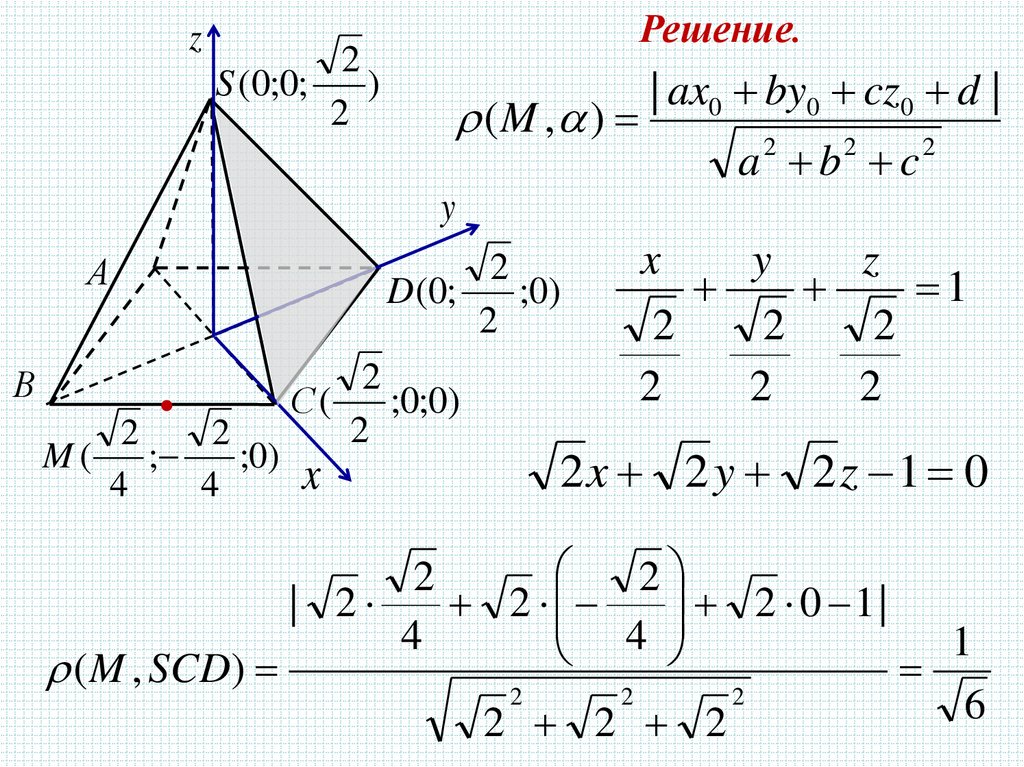
zРешение.
2
S (0;0;
)
2
(M , )
| ax0 by0 cz0 d |
a 2 b2 c2
y
А
В
2
2
M(
;
;0)
4
4
2
D (0;
;0)
2
2
С(
;0;0)
2
x
x
y
z
1
2
2
2
2
2
2
2x 2 y 2z 1 0
2
2
2 0 1|
| 2
2
4
4
1
( M , SCD)
2
2
2
6
2 2 2
19.
Угол между плоскостями: a1x b1 y c1z d1 0
Вектор нормали плоскости : n1{a1 ; b1 ; c1}
: a2 x b2 y c2 z d2 0
Вектор нормали плоскости : n2 {a2 ; b2 ; c2 }
cos
| a1 a2 b1 b2 c1 c2 |
a1 b1 c1 a2 b2 c2
2
2
2
2
2
2
20.
Угол между плоскостями равен углу междуперпендикулярами к этим плоскостям.
a1 x b1 y c1 z d1 0 уравнение плоскости
a2 x b2 y c2 z d 2 0 уравнение плоскости
m a1 ; b1 ; c1
n
n a2 ; b2 ; c2
cos m;n
m
a1a2 b1b2 c1c2
a b c
2
1
2
1
2
1
a b c
2
2
2
2
2
2
21.
Задача 10. В единичном кубеA...D1найдите угол
между плоскостями AD1 E и D1FC , где Е – середина
ребра А1В1 , а F – середина ребра B1С1
Решение.
z
Е
А1
B1
A(0;0;0)
С1
B
А
D
x
С
D1 (1;0;1)
ax by cz d 0
F
D1
1
Е (0; ;1)
2
y
d 0
a c d 0
1
b c d 0
2
Уравнение плоскости
с а
b 2a
ax 2ay az 0
AD1E : x 2 y z 0
Вектор нормали плоскости
AD1E :
n1{1;2; 1}
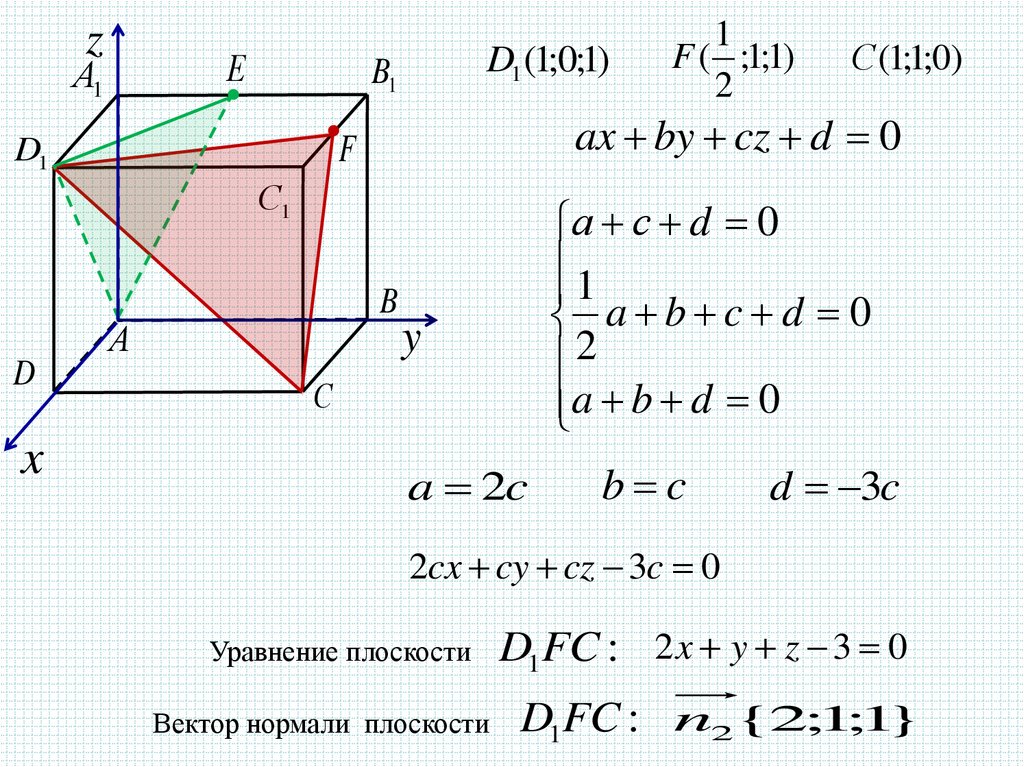
22.
zЕ
А1
D1 (1;0;1)
B1
С1
B
А
D
x
С (1;1;0)
ax by cz d 0
F
D1
1
F ( ;1;1)
2
а с d 0
1
a b c d 0
2
a b d 0
y
С
a 2c
b c
d 3c
2cx cy cz 3c 0
Уравнение плоскости
Вектор нормали плоскости
D1FC : 2 x y z 3 0
D1FC : n2{2;1;1}
23.
cos| a1 a2 b1 b2 c1 c2 |
a1 b1 c1 a2 b2 c2
2
2
2
n1{1;2; 1}
2
2
2
n2 {2;1;1}
| 1 2 2 1 1 1 |
1
cos
12 2 2 ( 1) 2 2 2 12 12 2
3
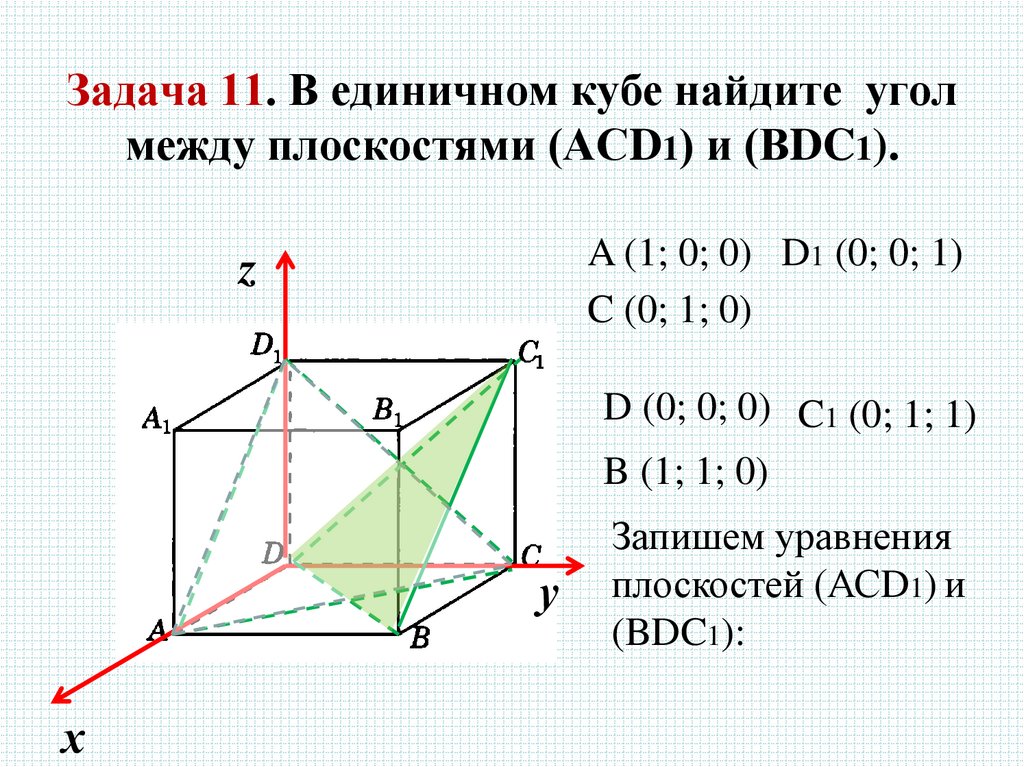
24. Задача 11. В единичном кубе найдите угол между плоскостями (АСD1) и (ВDC1).
A (1; 0; 0) D1 (0; 0; 1)C (0; 1; 0)
z
D (0; 0; 0) C1 (0; 1; 1)
B (1; 1; 0)
у
х
Запишем уравнения
плоскостей (АСD1) и
(BDC1):
25.
ax by cz d 0a d 0
b d 0
c d 0
a d
b d
c d
dx dy dz d 0
d 0
a b d 0
b c d 0
d 0
a b
c b
bx by bz 0
A (1; 0; 0)
C (0; 1; 0)
D1 (0; 0; 1)
D (0; 0; 0)
B (1; 1; 0)
C1 (0; 1; 1)
cos m;n
x y z 1 0
m 1;1;1 ACD1
x y z 0
n 1; 1;1 DBC1
1 1 1 1 1 1
1 1 1 1 1 1
m; n arccos
2
1
3
2
2
2
2
1
Ответ: arccos
3
2
1
3
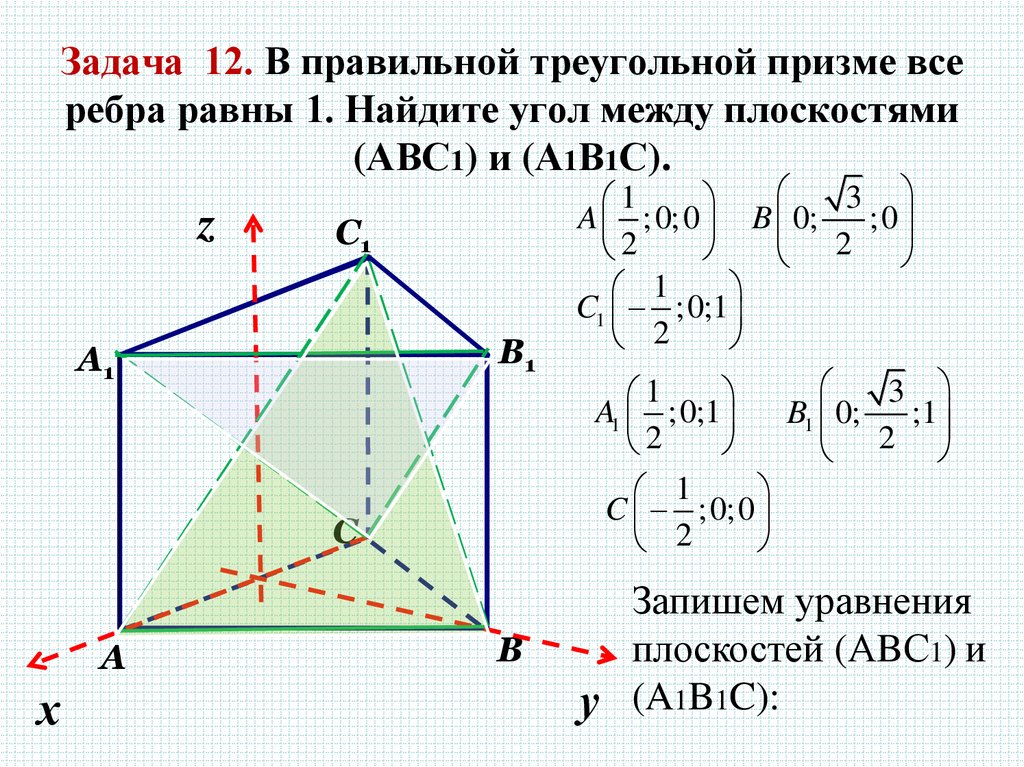
26. Задача 12. В правильной треугольной призме все ребра равны 1. Найдите угол между плоскостями (АВС1) и (А1В1С).
zС1
В1
А1
С
А
х
В
3
1
A ;0;0 B 0;
;0
2
2
1
C1 ;0;1
2
3
1
A1 ;0;1
B1 0;
;1
2
2
1
C ;0;0
2
Запишем уравнения
плоскостей (АBС1) и
у (A1B1C):
27.
1A ;0;0
2
ax by cz d 0
1
2 a d 0
3
B 0;
;0 3 b d 0
2 2
1
1 a c d 0
C1 ;0;1
2
2
1
A1 ;0;1
2
3
B1 0;
;1
2
1
C ;0;0
2
1
2 a c d 0
3
b c d 0
2
1
2 a d 0
a 2d
2
b
d
3
c 2d
a 2d
2
d
b
3
c 2d
2
dy 2dz d 0
3
2
2x
y 2z 1 0
3
2dx
2
m 2;
; 2 ABC1
3
2
2dx
dy 2dz d 0
3
2x
2
y 2z 1 0
3
2
n 2;
; 2 A1 B1C
3
28.
2n 2;
; 2
3
2
m 2;
; 2
3
cos m;n
2 2
2 2
2 2
3 3
2
1
2
2
7
2
2
2
2
2
22
2
2
3
3
1
m; n arccos
7
1
Ответ: arccos
7
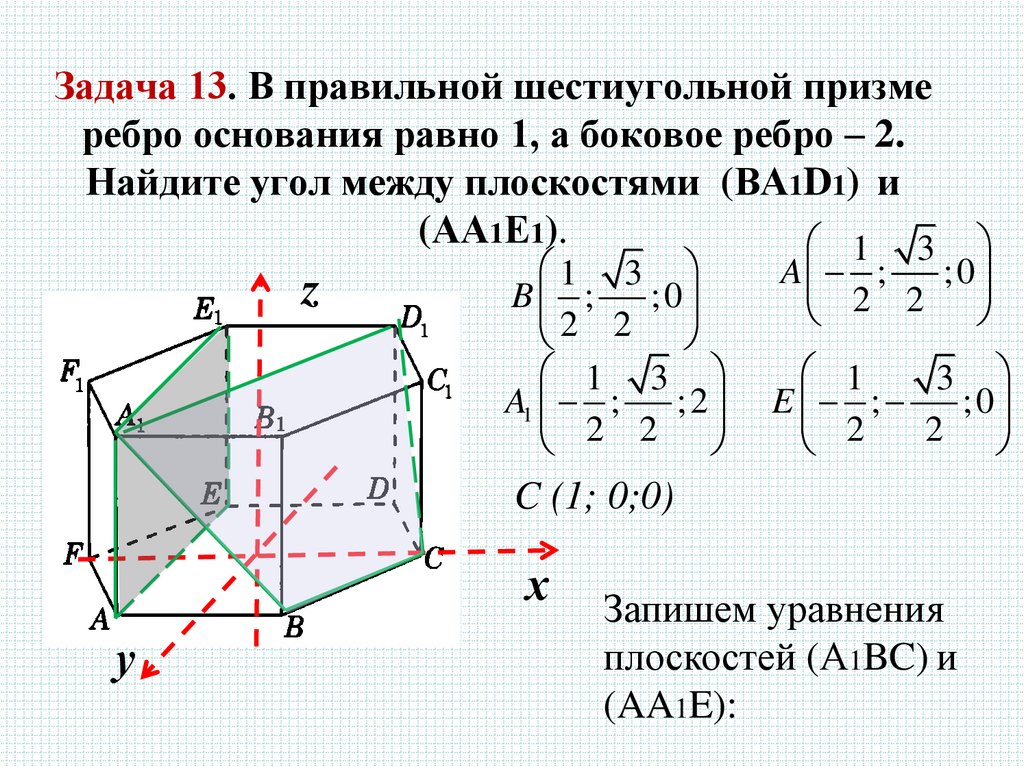
29. Задача 13. В правильной шестиугольной призме ребро основания равно 1, а боковое ребро – 2. Найдите угол между плоскостями
(ВА1D1) и(АА1Е1).
1 3
z
1 3
B ;
;0
2 2
1 3
A1 ;
; 2
2 2
A ;
;0
2 2
1
3
E ;
;0
2
2
C (1; 0;0)
х
у
Запишем уравнения
плоскостей (А1BC) и
(AA1E):
30.
ax by cz d 01 3
B ;
;0
2 2
1 3
A1 ;
; 2
2 2
C (1; 0;0)
1
3
b d 0
a
2
2
1
3
a
b 2c d 0
2
2
a d 0
1
1
dx
dy dz d 0
2
3
1
1
x
y z 1 0
2
3
a d
1
b
d
3
1
c d
2
1 1
m 1;
; A1 BC
3 2
31.
1A ;
2
1
A1 ;
2
3
;0
2
3
; 2
2
1
3
E ;
;0
2
2
ax by cz d 0
1
a
2
1
a
2
1
a
2
3
b d 0
2
3
b 2c d 0
2
3
b d 0
2
2dx 0 y 0 z d 0
2x 0 y 0 z 1 0
n 2; 0; 0 A1 AE
a 2d
b 0
c 0
32.
1 1m 1;
;
3 2
cos m;n
n 2; 0; 0
1
1
1 2
0 0
2
3
2
2
1 1
2
2
2
12
2
0
0
3 2
12
19
12
m; n arccos
19
12
Ответ: arccos
19
33.
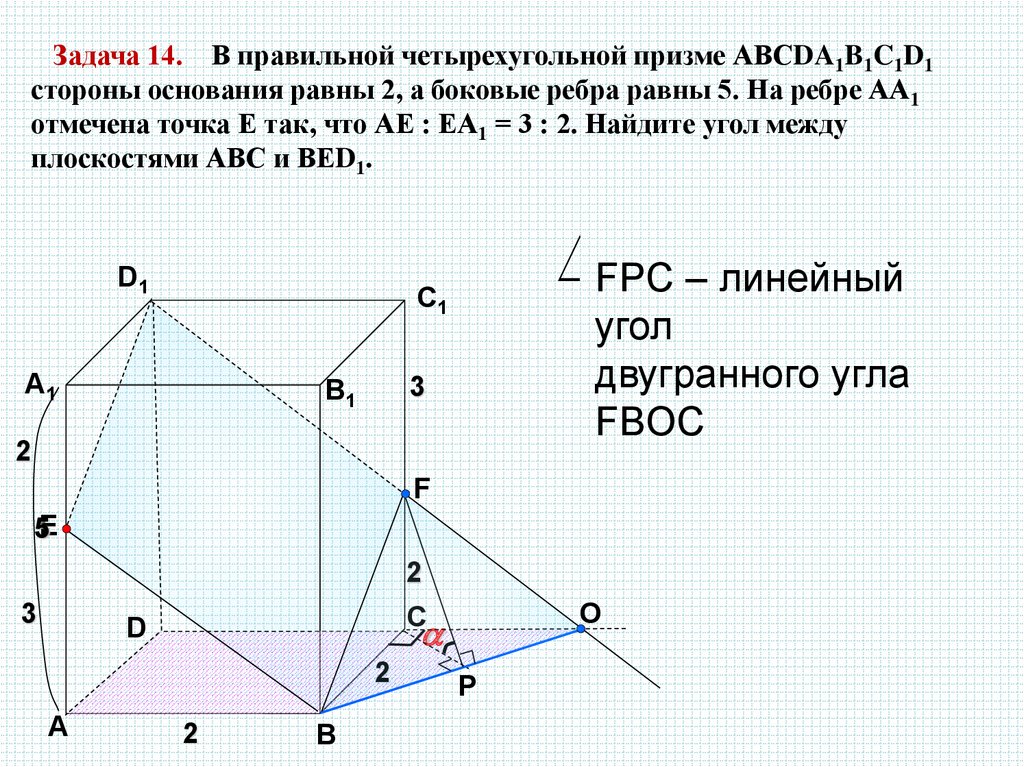
Задача 14. В правильной четырехугольной призме АВСDA1B1C1D1стороны основания равны 2, а боковые ребра равны 5. На ребре АА1
отмечена точка Е так, что АЕ : ЕА1 = 3 : 2. Найдите угол между
плоскостями АВС и ВЕD1.
D1
FPC – линейный
C1
A1
угол
двугранного угла
FBOC
3
B1
2
F
5E
2
3
2
А
O
C
D
2
В
P
34.
В правильной четырехугольной призме АВСDA1B1C1D1 стороныоснования равны 2, а боковые ребра равны 5. На ребре АА1 отмечена
точка Е так, что АЕ : ЕА1 = 3 : 2. Найдите угол между плоскостями АВС и
ВЕD1.
2 способ.
: a x b y c z d 0
1
1
1
1
Вектор нормали плоскости
D1
:
z
n1{a1 ; b1 ; c1}
a2 x b2 y c2 z d 2 0
Вектор нормали плоскости
:
n2 {a2 ; b2 ; c2 }
C1
cos
A1
B1
2
| a1 a2 b1 b2 c1 c2 |
a1 b1 c1
2
2
E(2;0;3), B(2;2;0),
F
2
n ( BED1 )
a2 b2 c2
2
2
a=c
d=-5c
b=1,5c
n
2x+3y+2z-10=0
{2;3;2}
D
2
А
x
2
В
y
cos
2
DD1 {0; 0;5},
D1 (0;0;5).
2a+3c+d=0
5c+d=0
2a+2b+d=0
E
5
3
:
0 2 0 3 5 2
0 2 0 2 5 2 2 2 32 2 2
2
17

















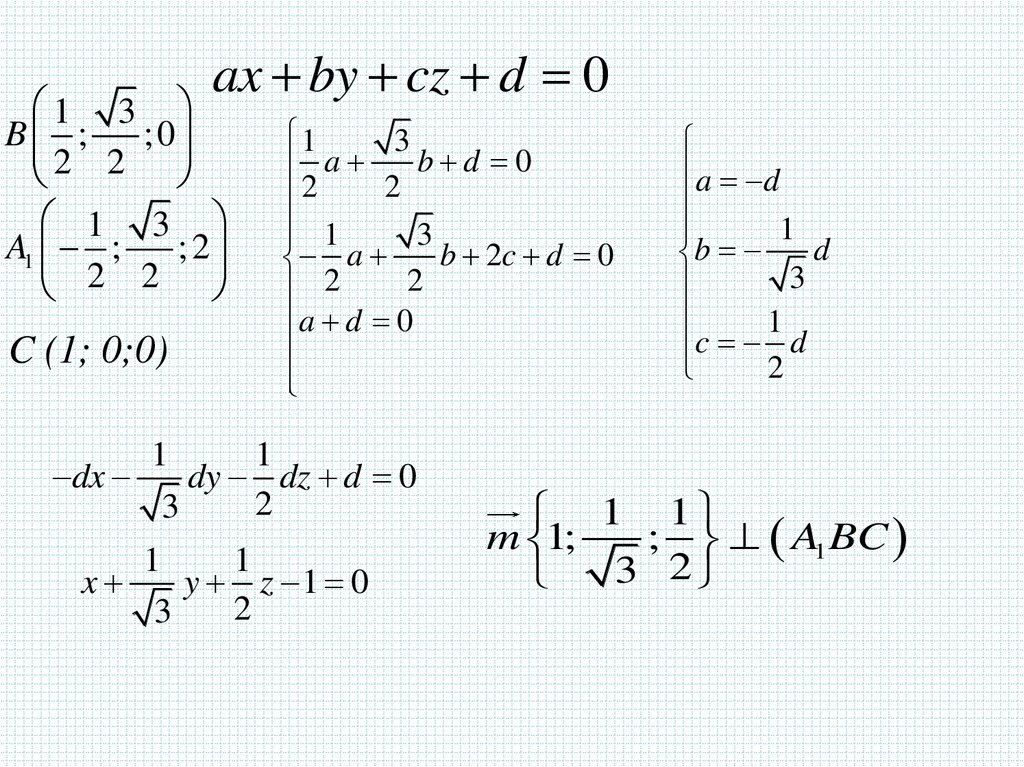



 Математика
Математика








