Касательная к окружности. Окружность, вписанная в угол

1.

Касательная к окружности.
Окружность, вписанная в угол
1

2.

Ваша задача на сегодня:
• Повтори материал со слайдов 3 – 4.
• Ознакомьтесь с материалом на слайдах 5-9.
• Выпишите: определение касательной к
окружности; свойство касательной; признак
касательной; свойство касательных, проходящих
через одну точку.
• Решите задачи по готовым чертежам со
слайдов 10 – 12 (запишите краткое решение и
ответ).
• Выполните задания по учебнику со слайда 11
(для каждой задачи вы должны построить
рисунок, записать дано, решение и ответ).
2

3.

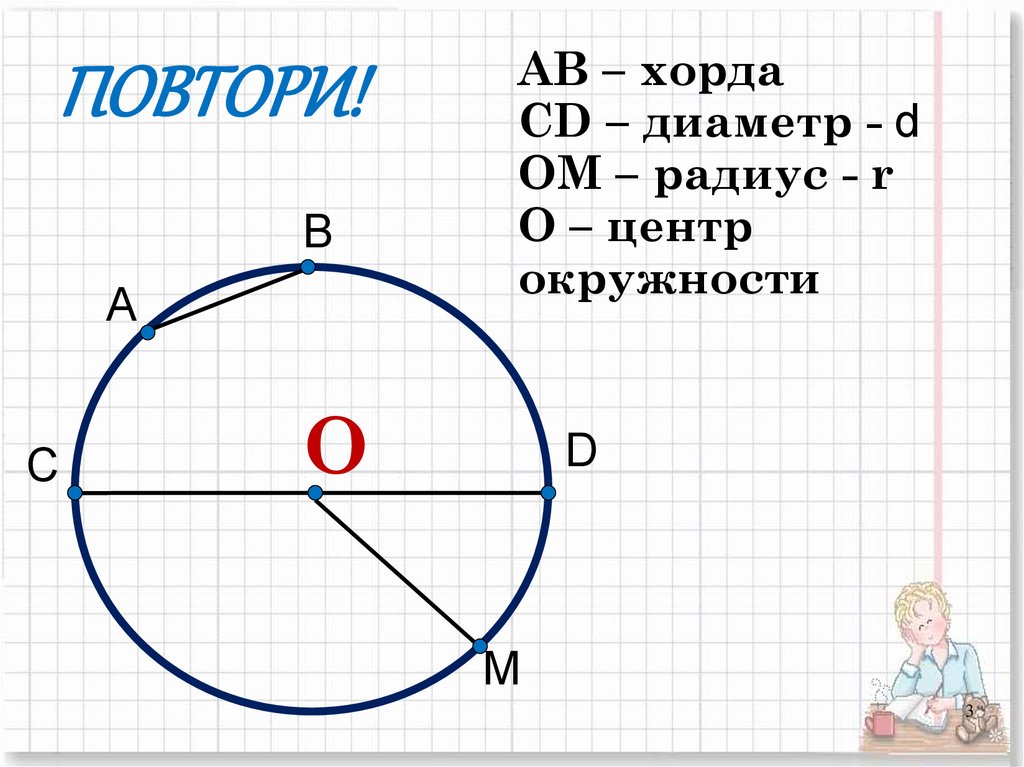
ПОВТОРИ!
В
А
С
АВ – хорда
СD – диаметр - d
ОМ – радиус - r
О – центр
окружности
О
D
М
3

4.

ПОВТОРИ!
Определения
• Окружность — геометрическая фигура на плоскости,
все точки которой равноудалены от данной точки
(центра окружности).
• Ра́диус (лат. radius — спица колеса, луч) — отрезок,
соединяющий центр окружности с любой точкой,
лежащей на окружности. Радиус составляет половину
диаметра.
• Диаметр — отрезок, соединяющий две точки на
окружности и проходящий через центр окружности.
Диаметр равен двум радиусам.
• Хо́рда (от греч. χορδή — струна) — отрезок,
соединяющий две точки окружности.
•Диаметр — это хорда, проходящая через центр
4

5.

Сколько общих точек могут
иметь прямая и окружность?
А
H
Н
В
d
d
r
О
r
d
О
r
О
d<r
d=r
две общие
точки
одна общая
точка
d>r
не имеют
общих точек

6.

Касательная к окружности
Определение:
Прямая, имеющая с
окружностью только
одну общую точку,
называется
касательной к
окружности, а их
общая точка
называется точкой
касания прямой и
окружности.
T
s=r
O

7.

Свойство касательной:
Касательная к окружности
перпендикулярна к радиусу,
проведенному в точку касания.
– касательная к
окружности с
центром О
Т – точка касания
OТ - радиус
Т
O

8.

8

9.

9

10.

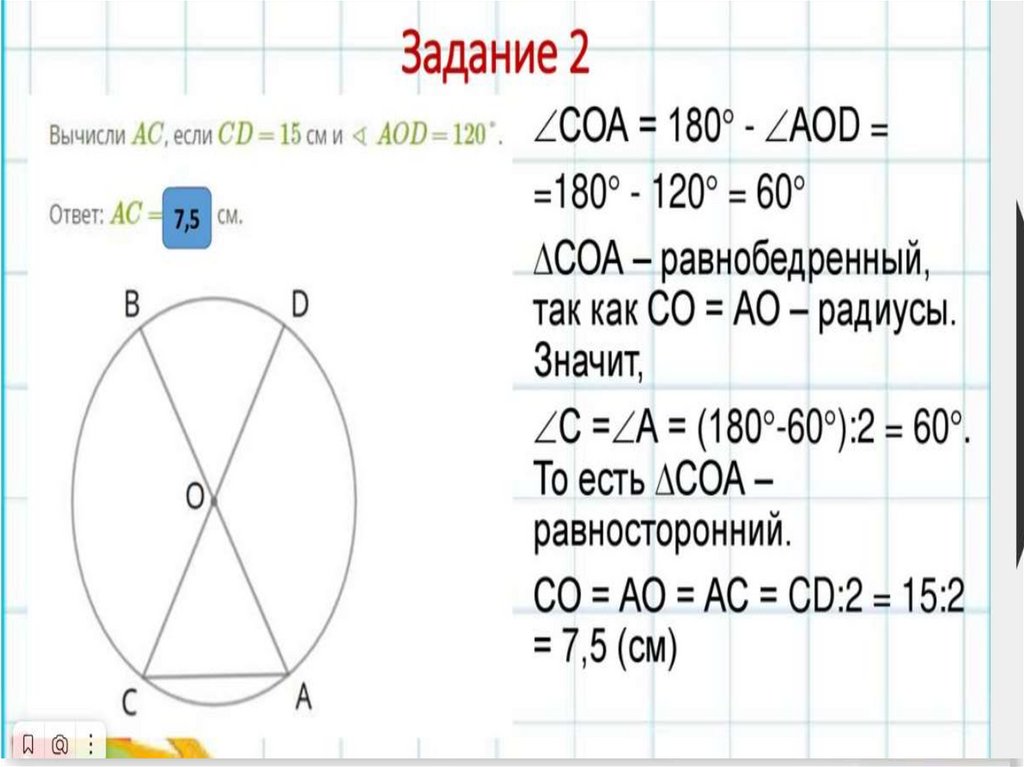
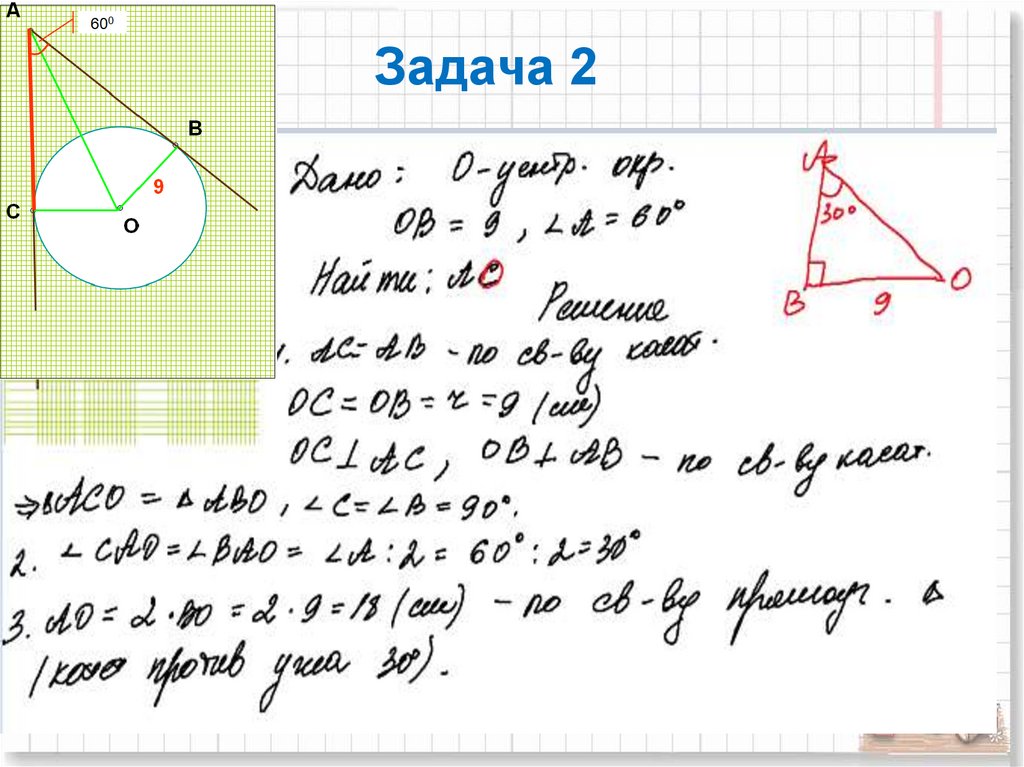
Задача 2
10

11.

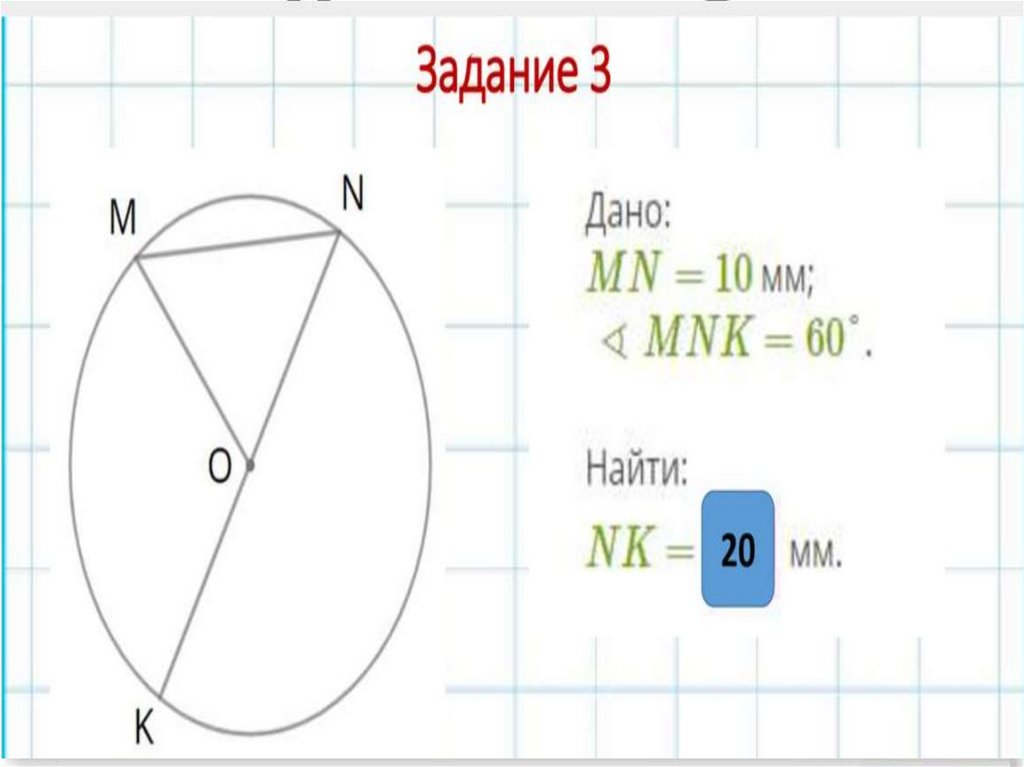
Задача 3
11

12.

Домашнее задание
1. Выучить правила: п. 70-71
стр.162-165
2. Решить в тетраде:
№631(а,б,д)+карточка
12

13.

СПАСИБО ЗА
ВНИМАНИЕ!