Окружность вписанная в угол

1.

21.03.2024
Классная работа
Окружность, вписанная
в угол

2.

Взаимное расположение
прямой и окружности
B
d
d
d
A
r
r
r
r
A
c
b
a
d b
d a
d c
d – расстояние от центра окружности до прямой.
d>r
a - прямая
d=r
b - касательная
А – точка касания
d< r
c - секущая

3.

Назови: радиус, диаметр, хорду, касательную, секущую
S
F
Q
A
C
M
O
R
X
N
B
D
T
K

4.

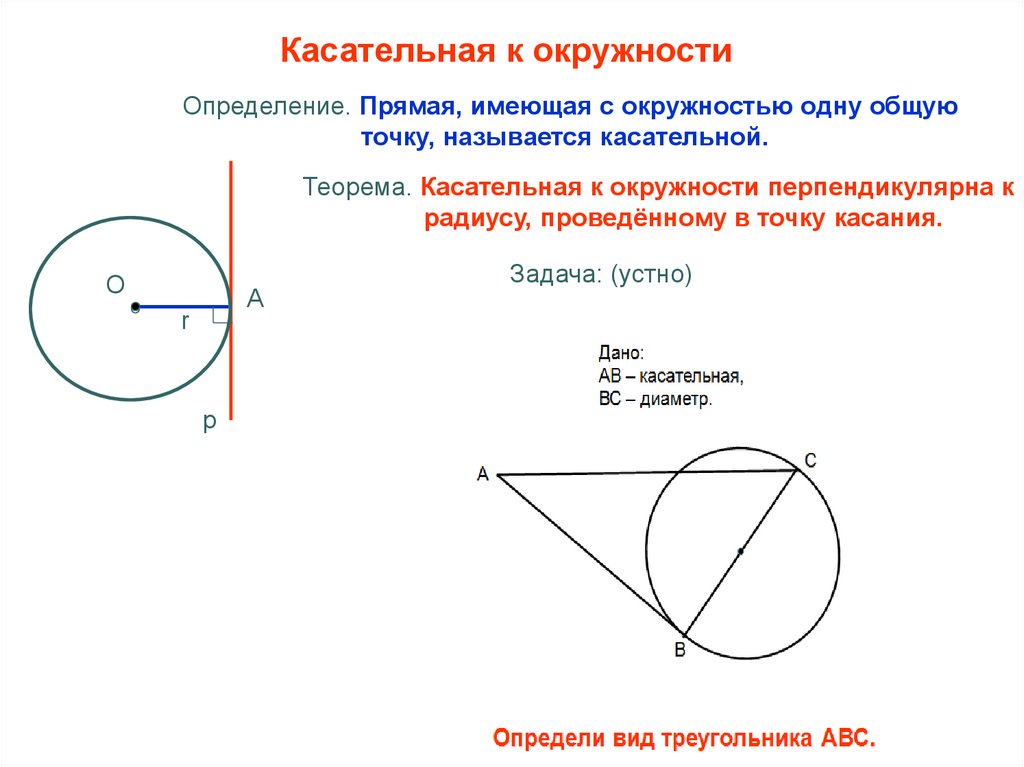
Касательная к окружности
Определение. Прямая, имеющая с окружностью одну общую
точку, называется касательной.
Теорема. Касательная к окружности перпендикулярна к
радиусу, проведённому в точку касания.
Задача: (устно)
О
A
r
р

5.

тест
1. Сколько касательных можно провести через данную точку
на окружности ?
а) одну;
б) две;
в) бесконечно много.
а
2. Сколько касательных можно провести через точку, не лежащую
на окружности
?
.
а) одну;
б) две;
в) бесконечно много.
б

6.

тест
3. Сколько окружностей можно провести, касающихся данной
прямой ?
а) одну;
б) две;
в) бесконечно много.
в

7.

тест
4. Сколько окружностей можно провести, касающихся
данной прямой в данной точке ?
а) одну;
б) две;
в) бесконечно много.
в

8.

тест
5. Сколько окружностей данного радиуса можно провести,
касающихся данной прямой в данной точке ?
а) одну;
б) две;
в) бесконечно много.
б

9.

Реши задачу
1.
C
O
r
A
b
D
Доказать: ОС = ОD.

10.

Важное свойство
С
Отрезки касательных к окружности, проведённые из
одной точки, равны и составляют равные углы с
прямой, проходящей через эту точку и центр
окружности.
r
Дано: Окр.(О; r), АВ и АС – касательные.
A
О
В
r
Доказать: АВ = АС,
ОАВ =
ОАС.
A
Дополнительные свойства:
С
1. АО – биссектриса ВАС.
К
r
О
r
В
2. ОА ВС.
3. СК = ВК.

11.

Реши задачу
С
A
Найти ВАС,
если ОА = 2r.
В
600

12.

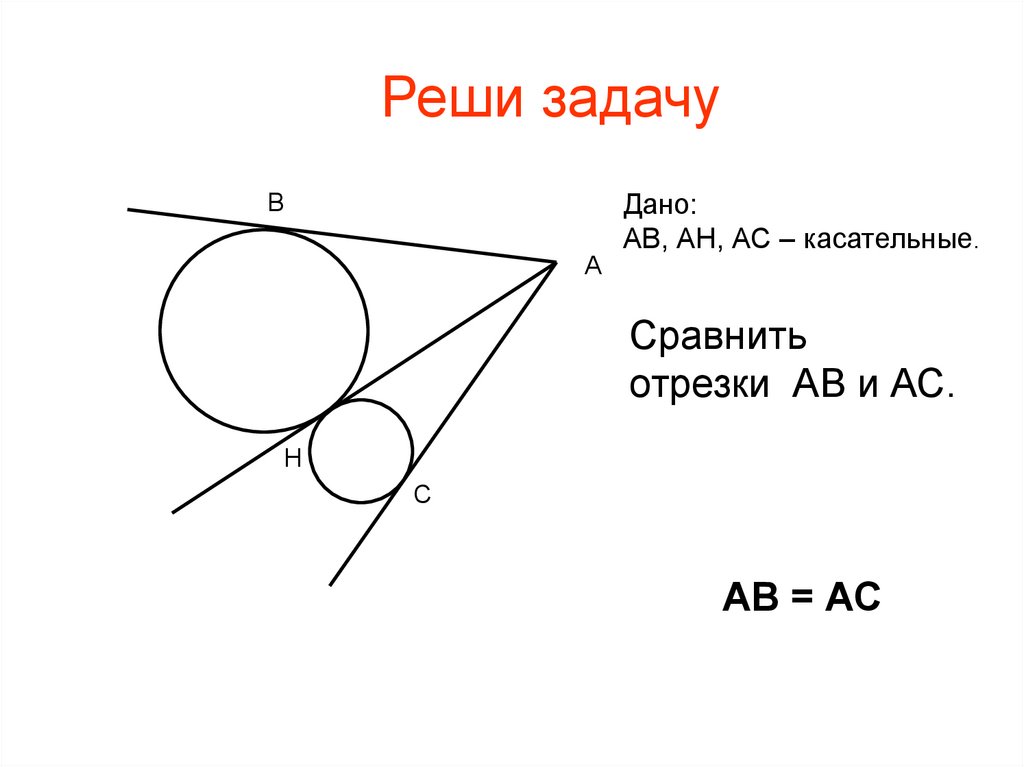
Реши задачу
В
А
Дано:
АВ, АН, АС – касательные.
Сравнить
отрезки АВ и АС.
Н
С
АВ = АС

13.

Реши задачу
K
O1
A
M
O
C
Доказать: АВ = СК
B

14.

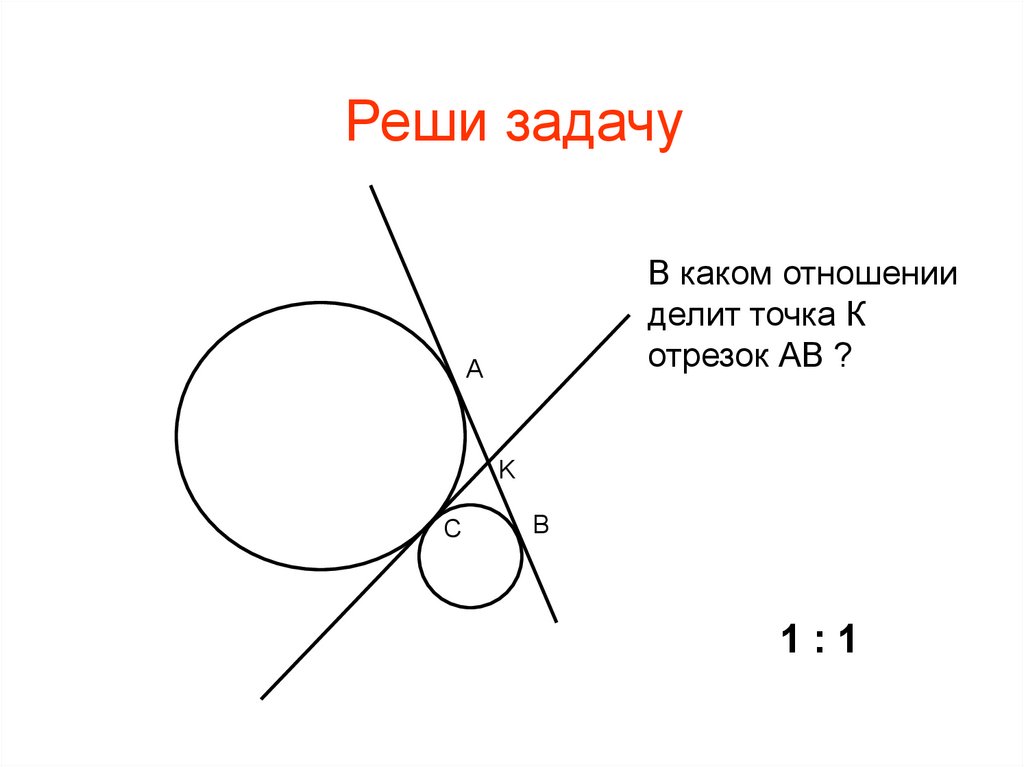
Реши задачу
В каком отношении
делит точка К
отрезок АВ ?
A
K
C
B
1:1

15.

Признак касательной
(теорема, обратная к свойству касательной)
Если прямая проходит через конец радиуса,
лежащий на окружности, и перпендикулярна
к этому радиусу, то она является касательной.
О
r
A
В

16.

Домашнее задание