Похожие презентации:
Окружность. Касательная к окружности. Центральные и вписанные углы
1. Урок по теме: «Окружность» 8 класс.
Автор проекта: Козлова Н.В.Учитель МОУ СОШ №23
2.
Мы предлагаем вам самостоятельно изучитьнекоторые вопросы по теме ,,Окружность,,
Для продолжения работы выбери
необходимый раздел.
1.Касательная к окружности.
2.Центральные и вписанные углы.
3.Проверь себя.
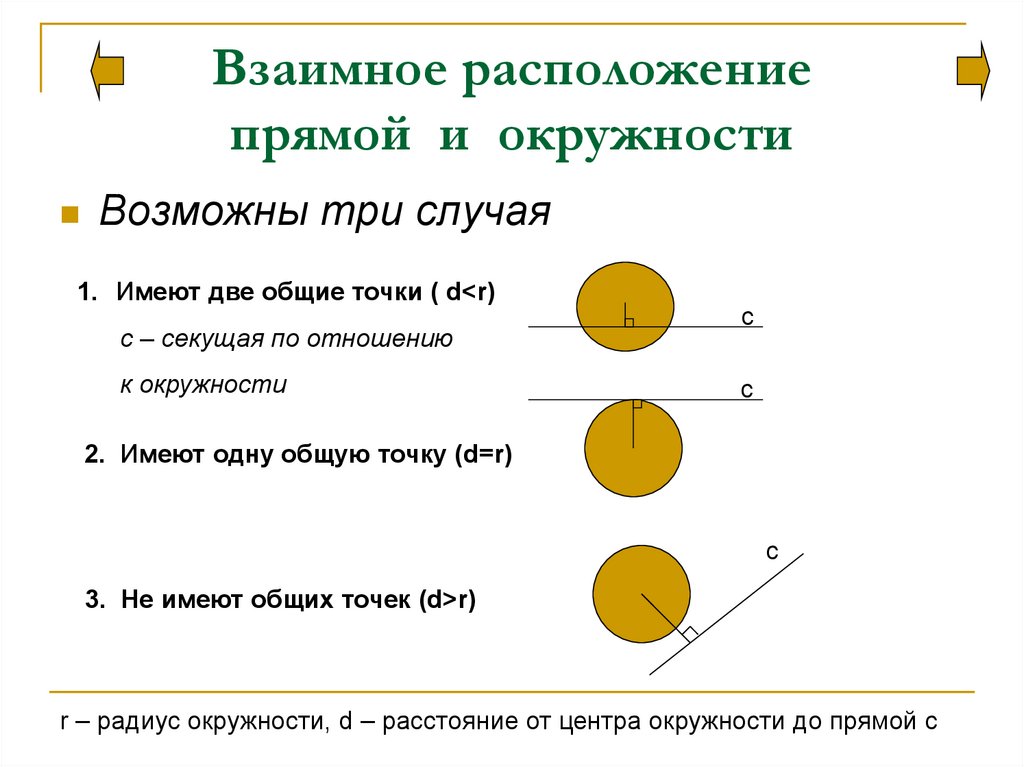
3. Взаимное расположение прямой и окружности
Возможны три случая1. Имеют две общие точки ( d<r)
с – секущая по отношению
к окружности
с
c
2. Имеют одну общую точку (d=r)
с
3. Не имеют общих точек (d>r)
r – радиус окружности, d – расстояние от центра окружности до прямой с
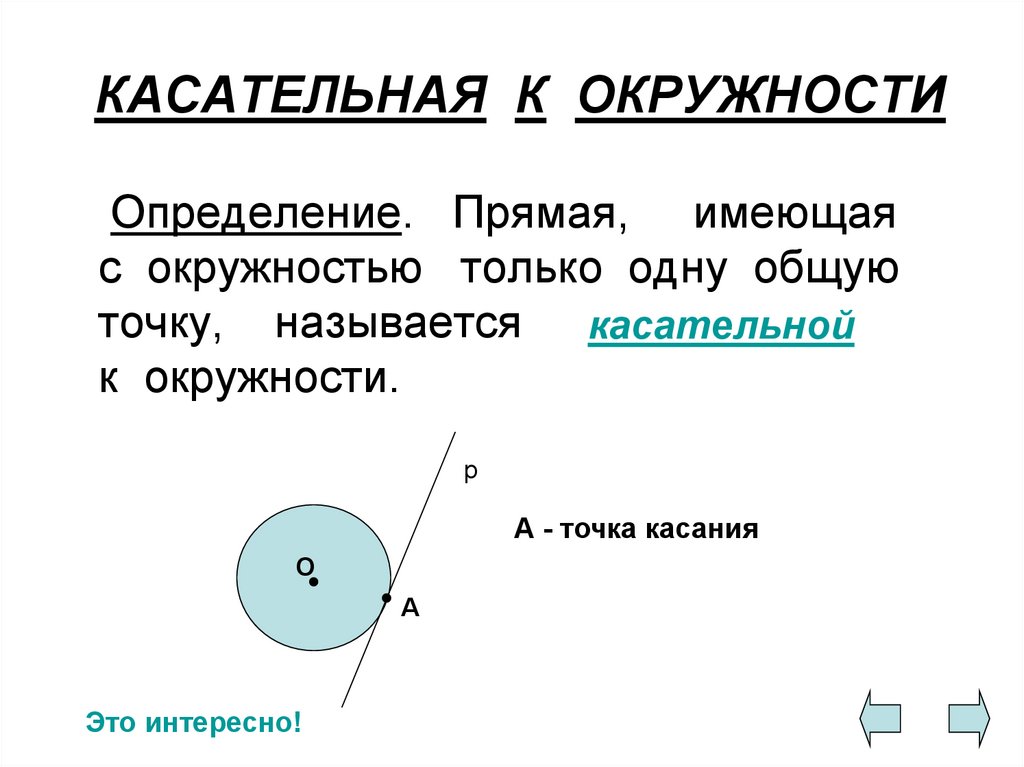
4. КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ
Определение. Прямая, имеющаяс окружностью только одну общую
точку, называется касательной
к окружности.
р
А - точка касания
О
А
Это интересно!
5.
(О свойстве касательной)Касательная к окружности перпендикулярна к радиусу,
проведенному в
точку
касания.
Дано: окр(О,ОА), р – касательная к окружности,
А – точка касания.
О
Доказать: р
А
р
ОА.
Доказательство:
1.Пусть р ОА, тогда ОА – наклонная к прямой р.
2.Т.к. п/р , проведенный из точки О к прямой р, меньше наклонной ОА,
то расстояние от центра О окружности до прямой р меньше радиуса.
3. Из пп. 1 и 2 прямая и окружность имеют две общие точки, что
противоречит условию ( прямая р – касательная ).
Т.об. р
ОА.
Ч. и т. д.
6.
.На рисунке точки А, В, С лежат на одной прямой.
А
В
С
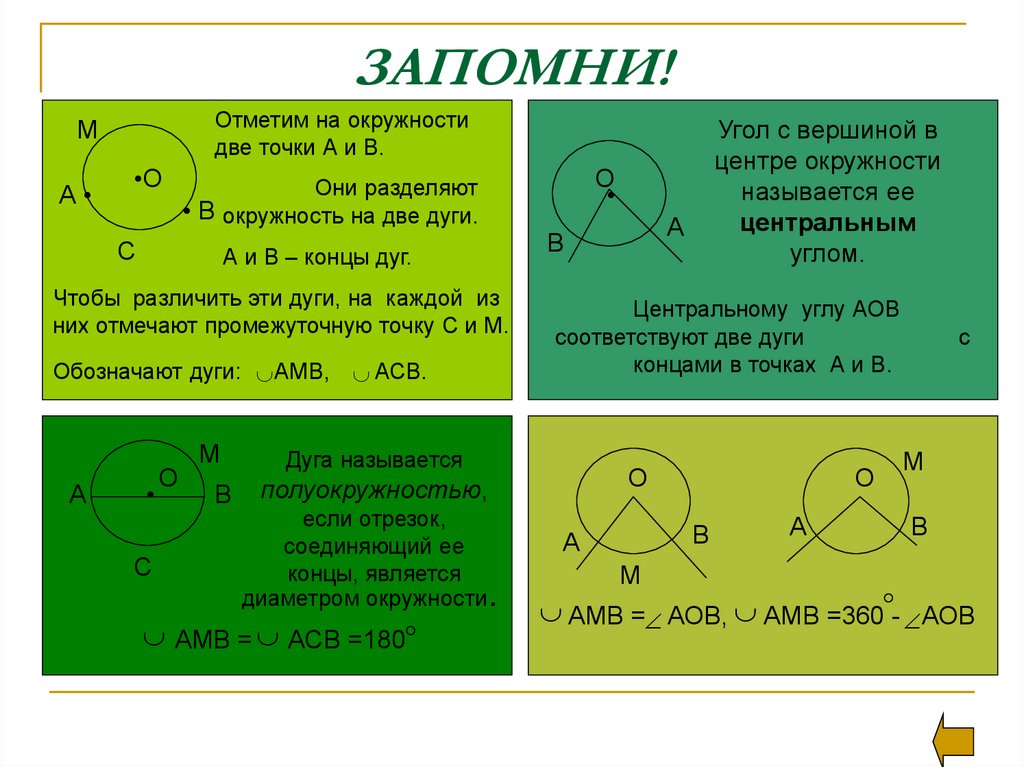
7. ЗАПОМНИ!
Отметим на окружностидве точки А и В.
М
А
•О
О
Они разделяют
• В окружность на две дуги.
С
дуги, на каждой из
Чтобы различить эти
них отмечают промежуточную точку С и М.
А
С
О
М
В
АСВ.
Центральному углу АОВ
соответствуют две дуги
концами в точках А и В.
Дуга называется
О
полуокружностью,
если отрезок,
соединяющий ее
концы, является
диаметром окружности
АМВ = АСВ =180
А
В
А и В – концы дуг.
Обозначают дуги: АМВ,
Угол с вершиной в
центре окружности
называется ее
центральным
углом.
В
А
.
О
А
с
М
В
М
АМВ = АОВ, АМВ =360 - АОВ
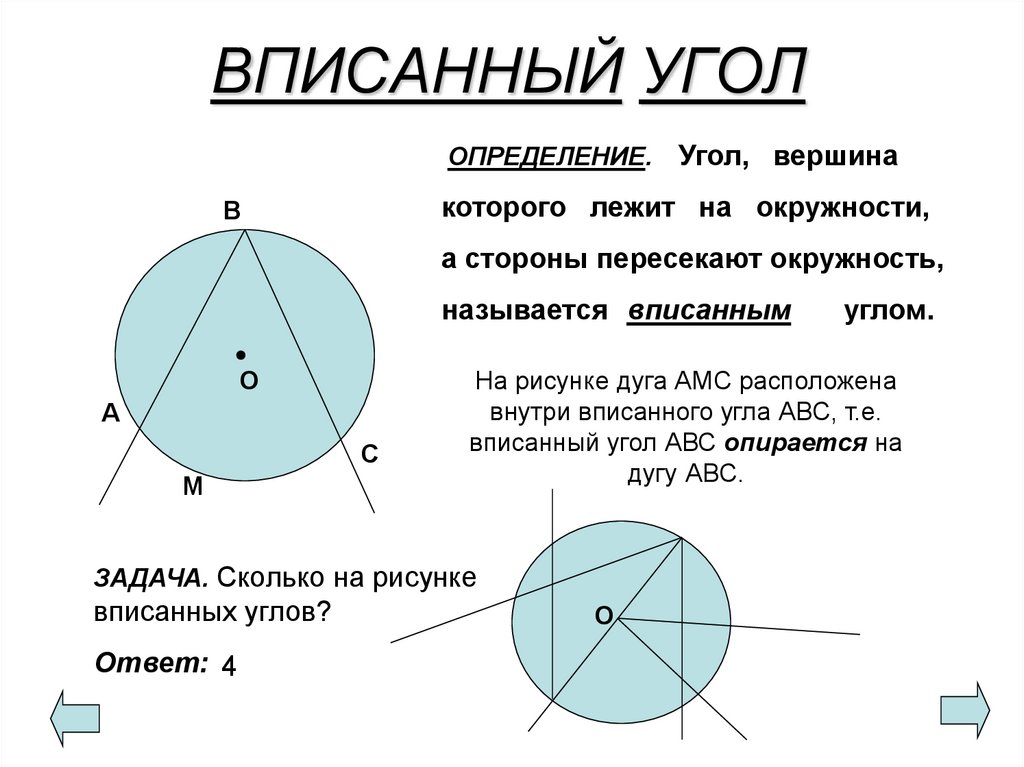
8. ВПИСАННЫЙ УГОЛ
ОПРЕДЕЛЕНИЕ.Угол, вершина
которого лежит на окружности,
В
а стороны пересекают окружность,
называется вписанным
О
А
С
М
На рисунке дуга АМС расположена
внутри вписанного угла АВС, т.е.
вписанный угол АВС опирается на
дугу АВС.
ЗАДАЧА. Сколько на рисунке
вписанных углов?
Ответ: 4
углом.
О
9.
Вписанный угол измеряется половиной дуги, на которую он опирается.Дано: окр.(О,r), АВС – вписанный (опирается на
АС).
В
1
2
Доказать: АВС =
АС.
1
А
2
О
Доказательство:
(рассмотрим случай, когда луч ВО совпадает с одной из
сторон АВС)
С
1. АОС =
АС, т.к.
АС меньше полуокружности.
2. АВО – р/б, т.к. АО = ВО = r 1 = 2 (свойство р/б тр -ка).
2
АС, т.е. 1 =
1 =
3. АОС = 1+ 2 = 2 1,т.к. АОС – внешний угол р/б тр-ка.
4. Из пп. 1и 3
Т. об. АВС = 1
АС.
2
1
АС.
2
Ч. и т. д.
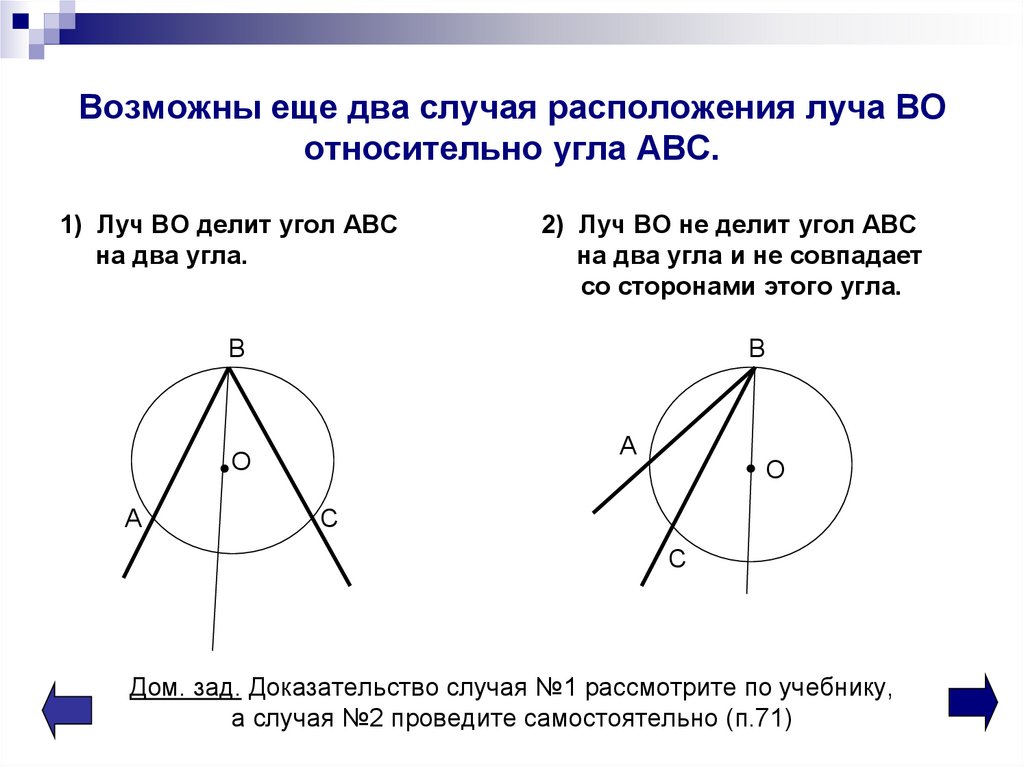
10. Возможны еще два случая расположения луча ВО относительно угла АВС.
1) Луч ВО делит угол АВСна два угла.
2) Луч ВО не делит угол АВС
на два угла и не совпадает
со сторонами этого угла.
В
В
А
О
А
О
С
С
Дом. зад. Доказательство случая №1 рассмотрите по учебнику,
а случая №2 проведите самостоятельно (п.71)
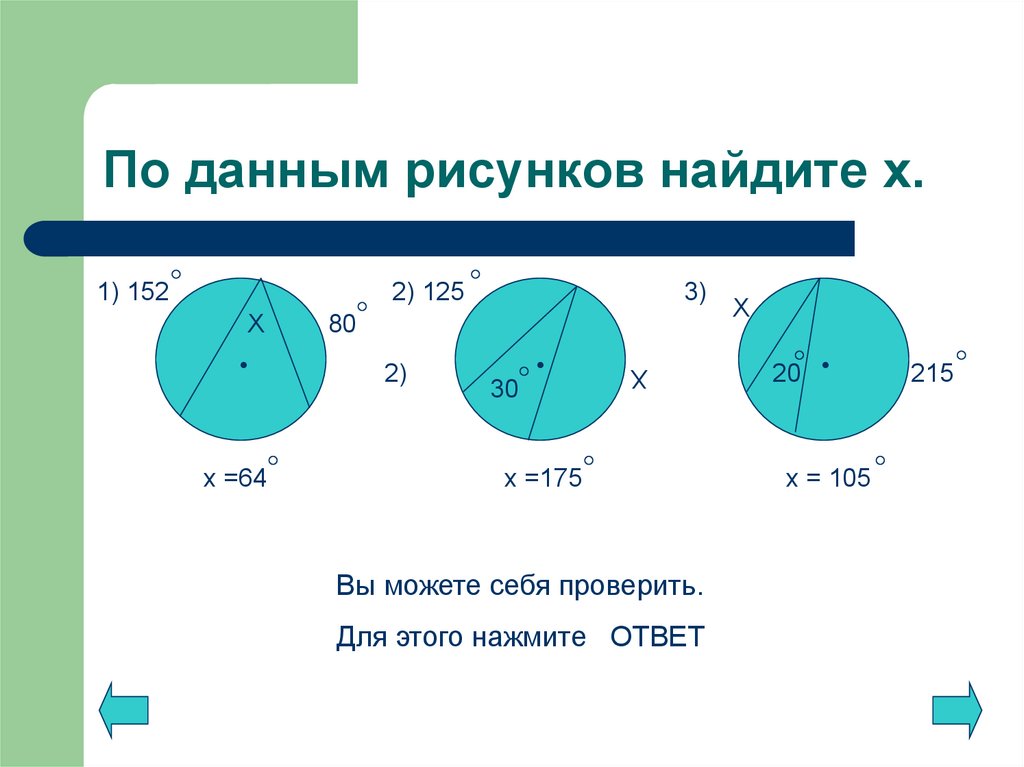
11. По данным рисунков найдите х.
1) 1522) 125
х =64
80
2)
30
Х
Х
3)
х =175
Вы можете себя проверить.
Для этого нажмите ОТВЕТ
Х
20
х = 105
215
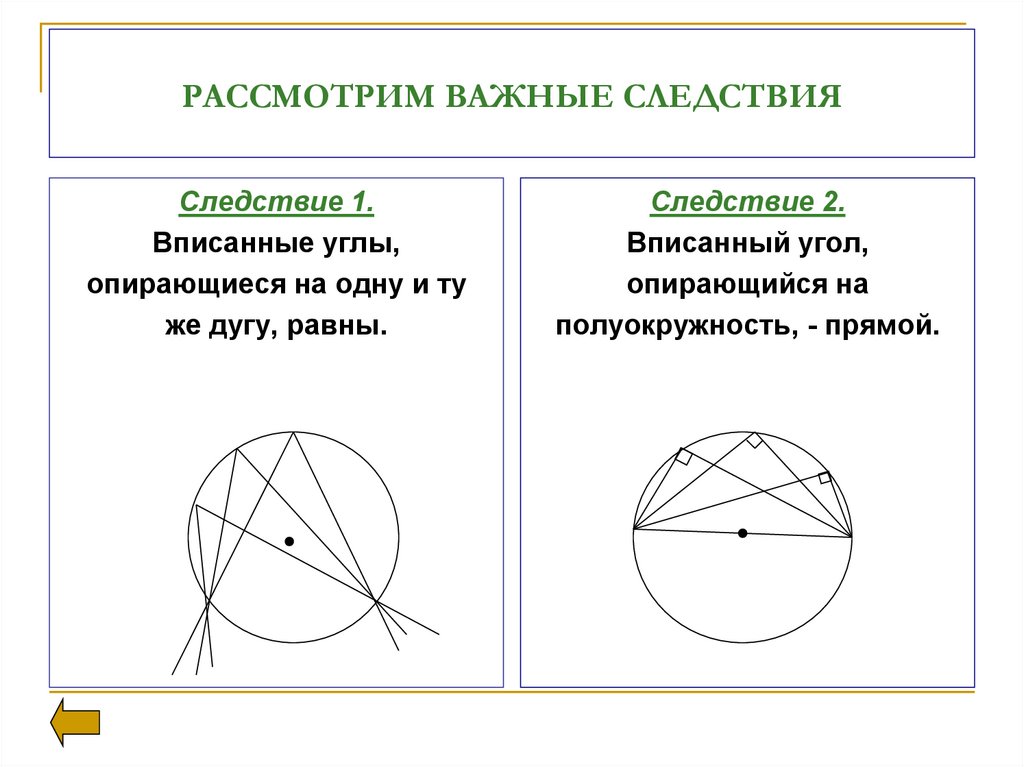
12. РАССМОТРИМ ВАЖНЫЕ СЛЕДСТВИЯ
Следствие 1.Вписанные углы,
опирающиеся на одну и ту
же дугу, равны.
Следствие 2.
Вписанный угол,
опирающийся на
полуокружность, - прямой.
13.
Каким может быть взаимное расположение прямой и окружности?
Как называется прямая, которая имеет с окружностью две общих точки?
Какая прямая называется касательной к окружности?
Какая точка называется точкой касания прямой и окружности?
Сформулируйте теорему о свойстве касательной ( к следующему уроку
попробуй выучить доказательство).
Какой угол называется центральным углом окружности?
Какая дуга называется полуокружностью?
Как определяется градусная мера дуги?
Какой угол называется вписанным?
Сформулируйте теорему о вписанном угле( к следующему уроку попробуй
разобрать все три случая доказательства).
Докажите, что вписанные углы, опирающиеся на одну и ту же дугу, равны.
Докажите, что вписанные углы, опирающиеся на полуокружность, - прямые.
14.
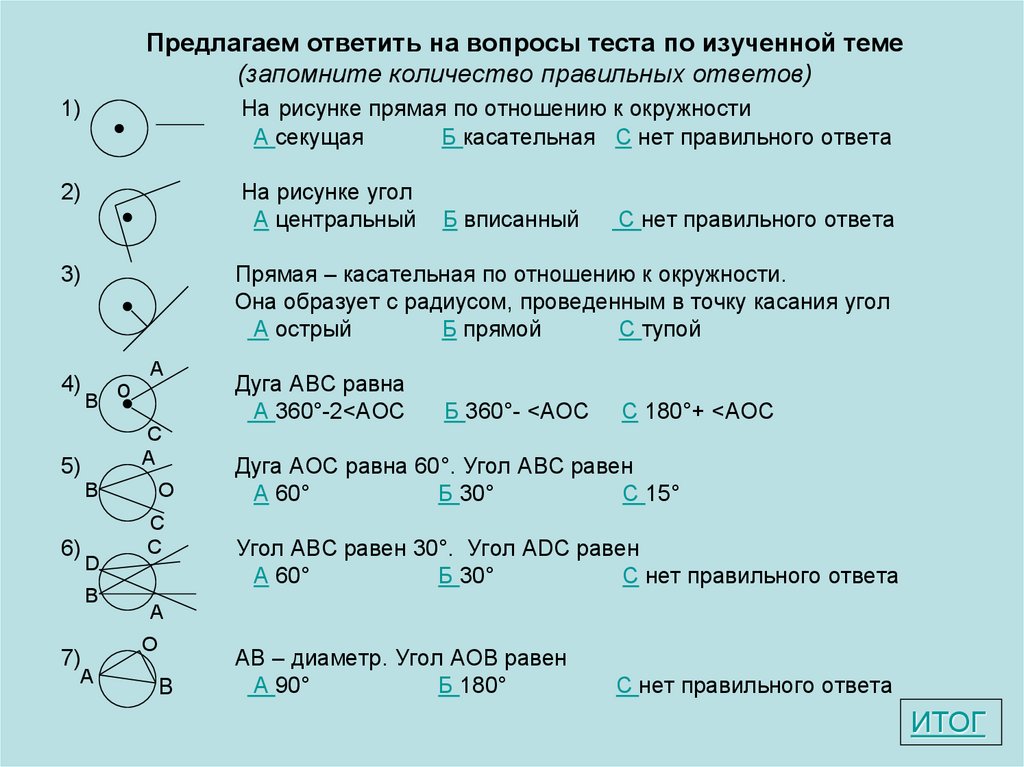
Предлагаем ответить на вопросы теста по изученной теме(запомните количество правильных ответов)
1)
На рисунке прямая по отношению к окружности
А секущая
Б касательная С нет правильного ответа
2)
На рисунке угол
А центральный
3)
4)
В
о
А
С
А
В
D
В
7)
С нет правильного ответа
Прямая – касательная по отношению к окружности.
Она образует с радиусом, проведенным в точку касания угол
А острый
Б прямой
С тупой
5)
6)
Б вписанный
А
О
С
C
Дуга АВС равна
А 360°-2<АОС
Б 360°- <АОС
С 180°+ <АОС
Дуга АОС равна 60°. Угол АВС равен
А 60°
Б 30°
С 15°
Угол АВС равен 30°. Угол АDС равен
А 60°
Б 30°
С нет правильного ответа
А
О
В
АВ – диаметр. Угол АОВ равен
А 90°
Б 180°
С нет правильного ответа
ИТОГ
15.
ПРАВИЛЬНОДля возвращения к тесту нажми
ОК
16.
ПОДУМАЙ ЕЩЕДля возвращения к тесту нажми
ОК
17. КРИТЕРИИ ОЦЕНКИ
количество правильныхответов
7
отметка
отлично
5-6
хорошо
4
удовлетворительно
менее 4
нельзя оценить
ответ
18.
ЕСЛИ ТЫ ДОВОЛЕН РЕЗУЛЬТАТОМ,ПОЗДРАВЛЯЕМ! ЖЕЛАЕМ УСПЕХОВ ПРИ
ИЗУЧЕНИИ ГЕОМЕТРИИ.
ЕСЛИ НЕ ВСЕ УДАЛОСЬ, ТО МОЖНО
ВЕРНУТЬСЯ НА ПЕРВЫЙ СЛАЙД








 Математика
Математика








