Похожие презентации:
Задание 13 (занятие 1). Профильный ЕГЭ по математике
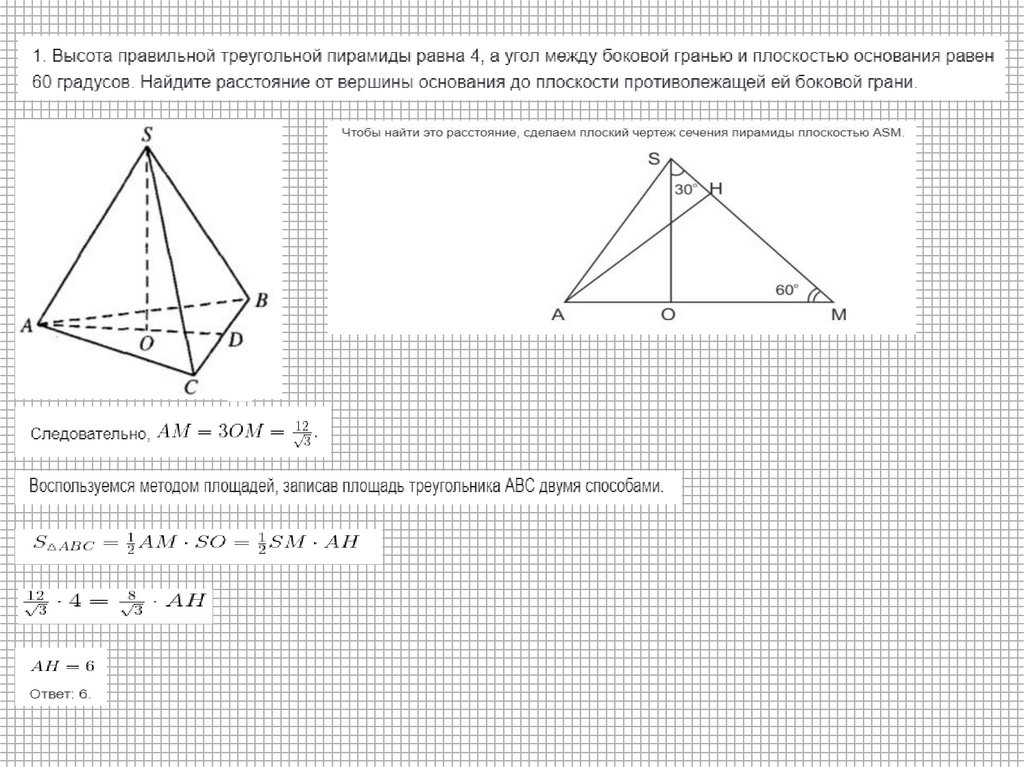
1.
Профильный ЕГЭПО МАТЕМАТИКЕ
СТЕРЕОМЕТРИЯ
Задание 13 (занятие 1)
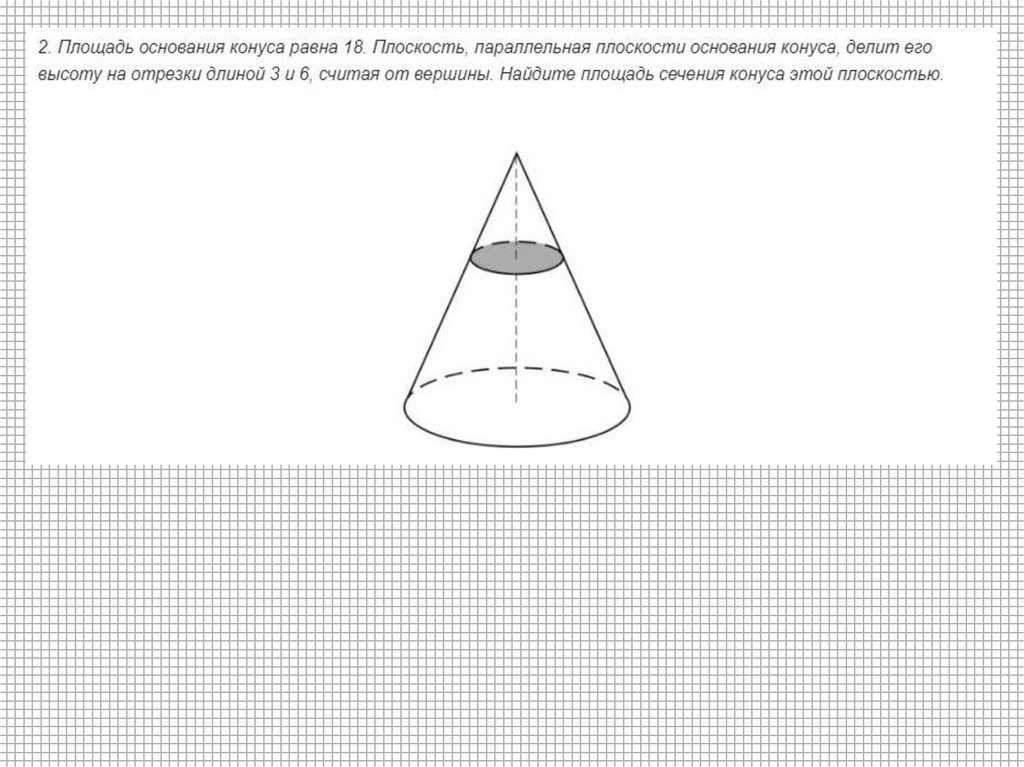
2.
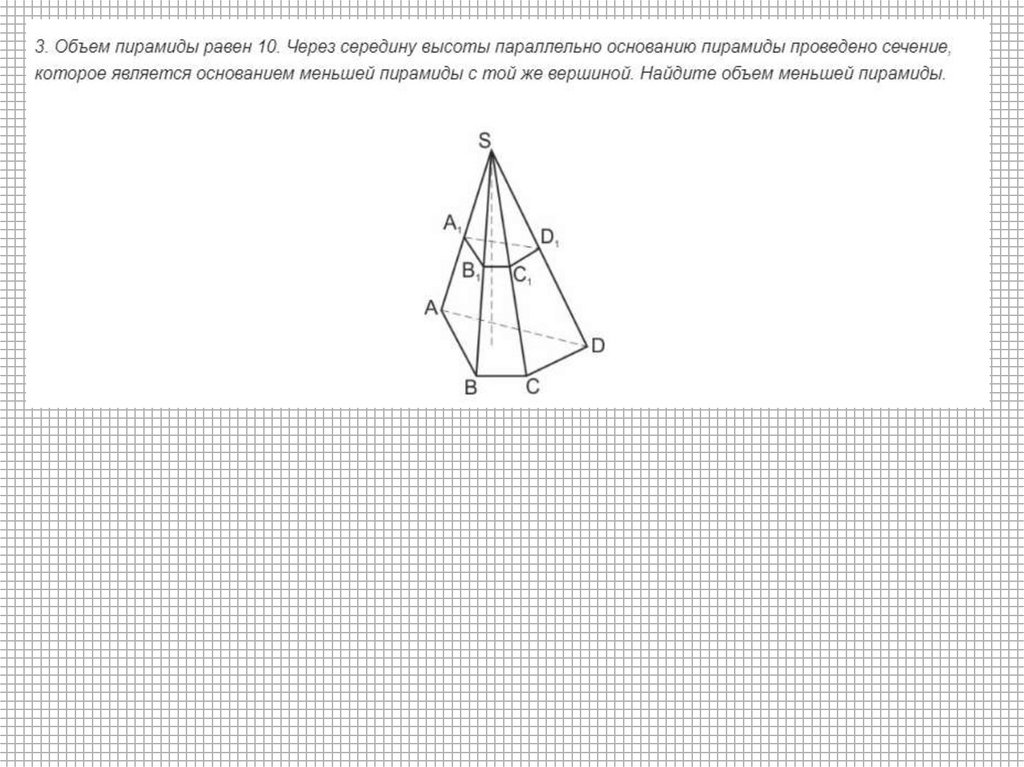
3.
Лайфхаки для решения задач по стереометрии1. Задача по стереометрии не решается
без хорошего чертежа.
2. Все, что нужно на чертеже
должно быть хорошо видно.
4.
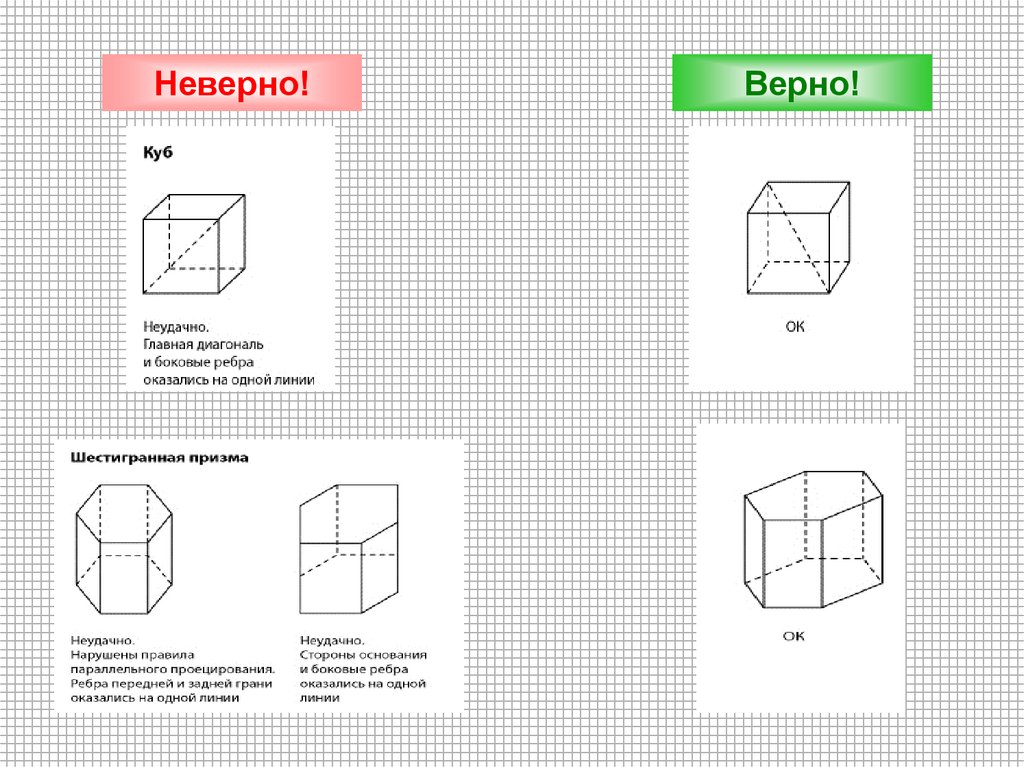
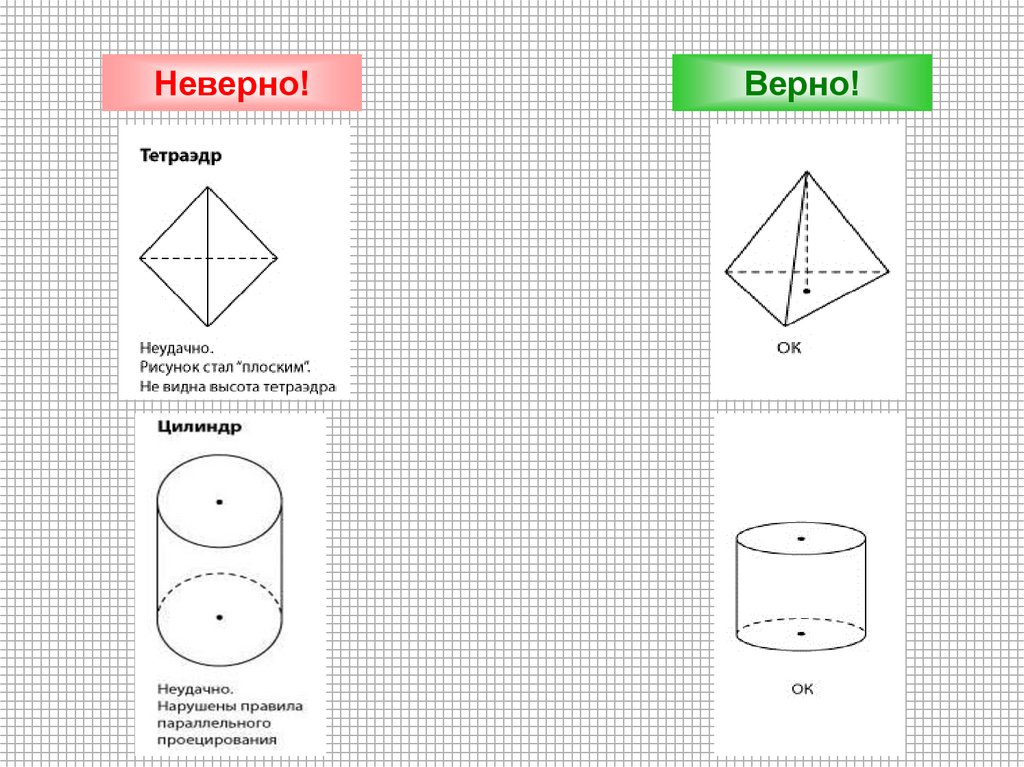
Неверно!Верно!
5.
Неверно!Верно!
6.
Неверно!Верно!
7.
Лайфхаки для решения задач по стереометрии3. Уметь записывать решение кратко.
8.
Лайфхаки для решения задач по стереометрии4. Почти в каждой задаче по стереометрии
встречаются особенные треугольники.
9.
Лайфхаки для решения задач по стереометрии5. Формула для площади прямоугольной проекции
фигуры помогает найти угол между плоскостями.
10.
Лайфхаки для решения задач по стереометрии6. Метод объемов помогает найти
расстояние от точки до плоскости.
11.
Лайфхаки для решения задач по стереометрии7. Сначала изучаем «классику». После этого,
если есть время, можно браться и
за координатный метод.
12.
Несколько правил1. Начинай с построения чертежа
2. Записывай каждый шаг решения
3. Твоя цель – от объёмной задачи
перейти к плоской, планиметрической
13.
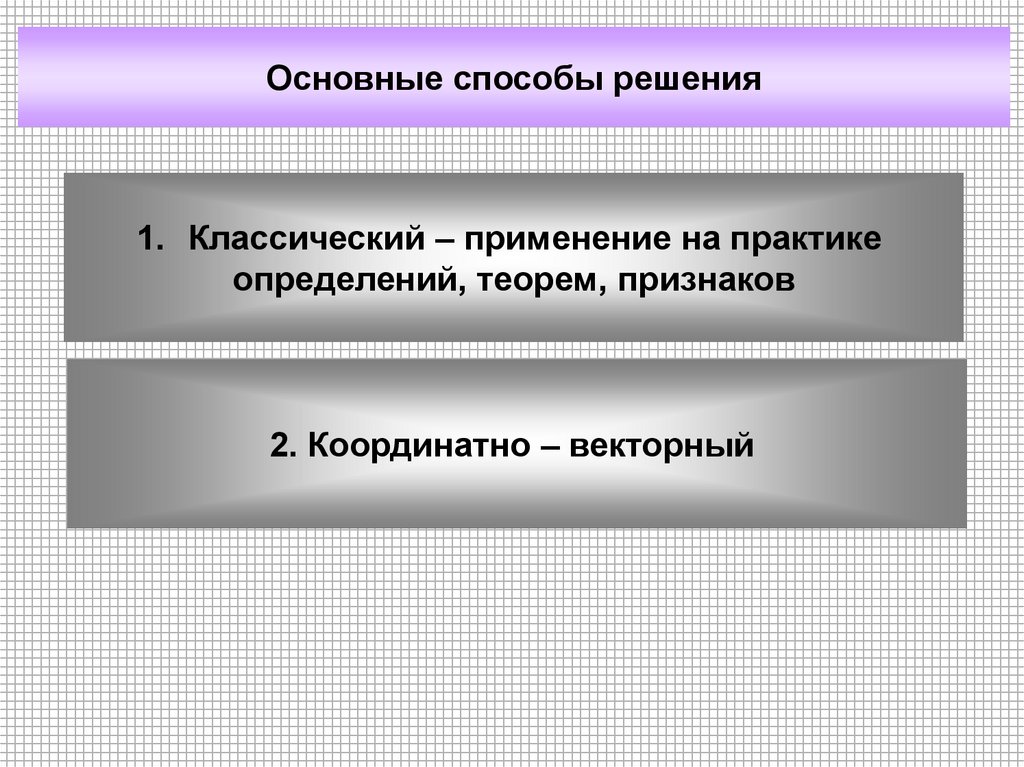
Основные способы решения1. Классический – применение на практике
определений, теорем, признаков
2. Координатно – векторный
14.
Задание 13Профильного ЕГЭ по математике состоит из двух пунктов.
Пункт (а)
– доказательство
какого-либо
утверждения
Пункт (б)
– вычисление
какой-либо
величины
Построение чертежа
15.
Типы задачМетоды решения
1) Находим угол между прямыми как угол треугольника (теорема косинусов). Пользуемся определением
угла между скрещивающимися прямыми.
Угол между прямыми
2) Возможно – применение теоремы о трех перпендикулярах
3) Векторно-координатный способ
1) По определению (как угол между прямой и ее проекцией на плоскость)
Угол между прямой и
плоскостью
2) Векторно-координатный способ
3) В случае перпендикулярности прямой и плоскости – доказываем, что прямая перпендикулярна двум
пересекающимся прямым, лежащим в плоскости
1) По определению (как угол между перпендикулярами, проведенными в этих плоскостях к линии их
пересечения)
Угол между плоскостями 2) С помощью формулы площади прямоугольной проекции фигуры
3) Векторно-координатный способ – как угол между нормалями к плоскостям
Расстояние от точки до
плоскости
Расстояние между
скрещивающимися
прямыми
Нахождение радиуса
сферы, вписанной в
многогранник
1) По определению (как длину перпендикуляра, опущенного из точки на плоскость)
2) С помощью метода объемов
3) Координатный способ. Пользуемся формулой расстояния от точки до плоскости.
1) По определению (как длину их общего перпендикуляра)
2) Как расстояние между одной из этих прямых и параллельной ей плоскостью, в которой лежит другая
прямая.
3) Как расстояние между параллельными плоскостями, в которых лежат эти прямые.
1) Находим центр сферы как точку, равноудаленную от всех граней многогранника
2) Разбиваем многогранник на пирамиды с общей вершиной в центре вписанной сферы. Представляем
объем многогранника как сумму объемов этих пирамид.






















 Математика
Математика








