Задания С-2 по математике ЕГЭ-2014

1. Задания С-2 по математике ЕГЭ-2014

2.

Угол между прямой и плоскостью
Угол между прямой и плоскостью — это угол между
прямой и ее проекцией на данную плоскость.
Определение. Прямая перпендикулярна
плоскости, если она перпендикулярна любой
прямой, лежащей в этой плоскости.
Признак. Прямая перпендикулярна плоскости,
если она перпендикулярна двум пересекающимся
прямым, лежащим в этой плоскости.

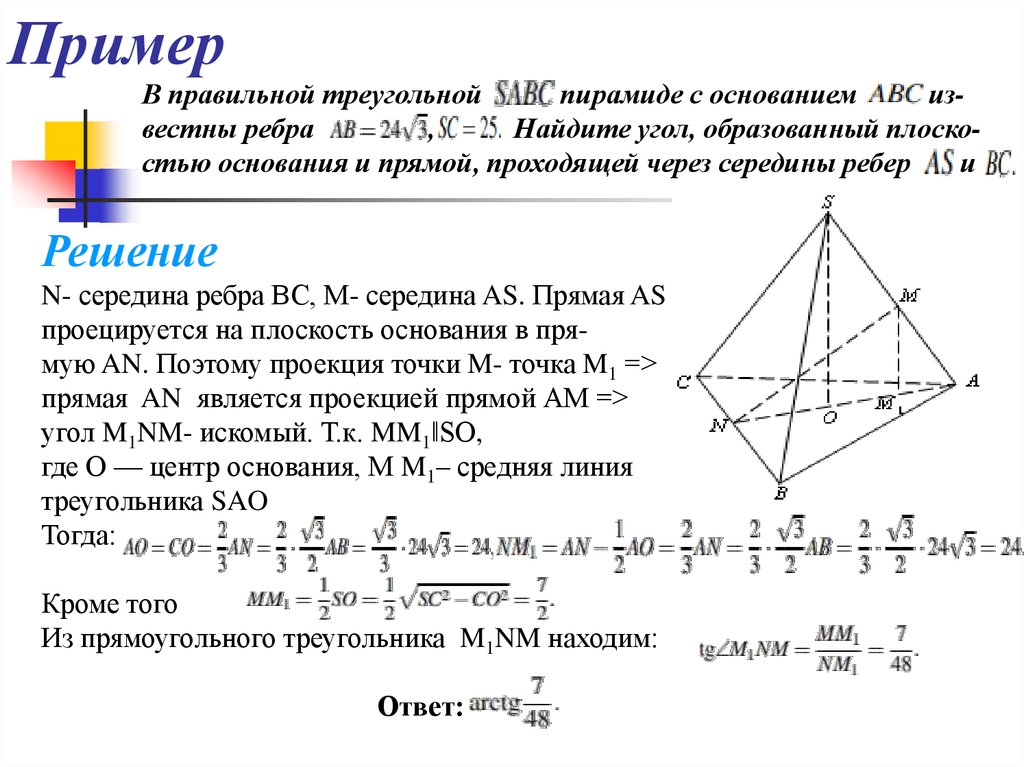
3. Пример

В правильной треугольной
пирамиде с основанием
известны ребра
,
Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер
и
Решение
N- середина ребра ВС, М- середина AS. Прямая AS
проецируется на плоскость основания в прямую AN. Поэтому проекция точки M- точка M1 =˃
прямая AN является проекцией прямой АМ =˃
угол M1NM- искомый. Т.к. MM1ǁSO,
где О — центр основания, М M1– средняя линия
треугольника SAO
Тогда:
Кроме того
Из прямоугольного треугольника M1NM находим:
Ответ:

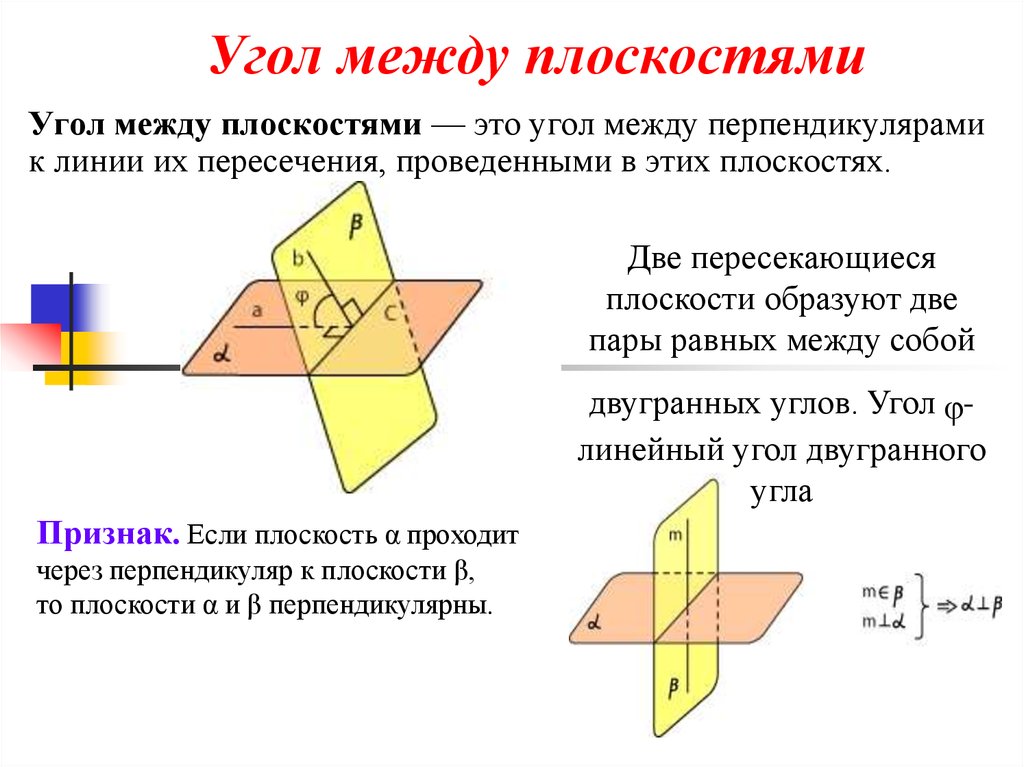
4. Угол между плоскостями

Угол между плоскостями — это угол между перпендикулярами
к линии их пересечения, проведенными в этих плоскостях.
Две пересекающиеся
плоскости образуют две
пары равных между собой
ᵩ
двугранных углов. Угол линейный угол двугранного
угла
Признак. Если плоскость α проходит
через перпендикуляр к плоскости β,
то плоскости α и β перпендикулярны.

5. Пример.

Дан прямоугольный параллелепипед АВСDA1B1C1D1,
в котором АВ=3, AD=2, АА1=7 и точка E делит сторону
АА1 в отношении 4 к 3, считая от точки А. Найдите
угол между плоскостями АВС и ВЕD1.
Решение
Построим искомый угол (Гиперссылки\1.docx) .Таким
образом, искомый угол между плоскостями АВС и BED1
равен углу АМЕ.
Найдем длины сторон треугольника АМЕ: так как
точка Е делит сторону АА1 в отношении 4 к 3, считая от
точки А, а длина стороны АА1 равна 7, то АЕ=4.
Чтобы найти АМ, рассмотрим прямоугольный
треугольник АВF: АМ- высота треугольника, АВ=2(по
условию), длину стороны АF мы можем найти из подобия
прямоугольных треугольников DD1F и AEF:

6.

По теореме Пифагора из треугольника АВF находим :
Длину АМ найдем через площади треугольника АBF:
1)
Откуда-
2)
Таким образом, из прямоугольного треугольника АЕМ имеем:
Тогда искомый угол между плоскостями АВС и BED1 равен
Ответ:

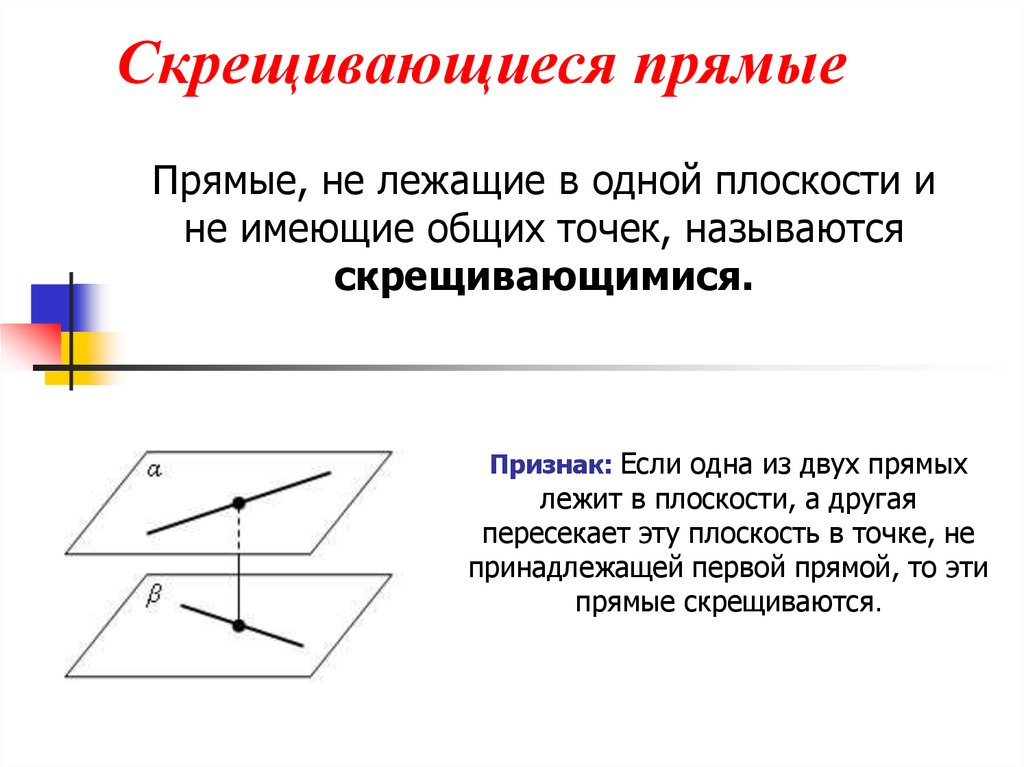
7. Скрещивающиеся прямые

Прямые, не лежащие в одной плоскости и
не имеющие общих точек, называются
скрещивающимися.
Признак: Если одна из двух прямых
лежит в плоскости, а другая
пересекает эту плоскость в точке, не
принадлежащей первой прямой, то эти
прямые скрещиваются.

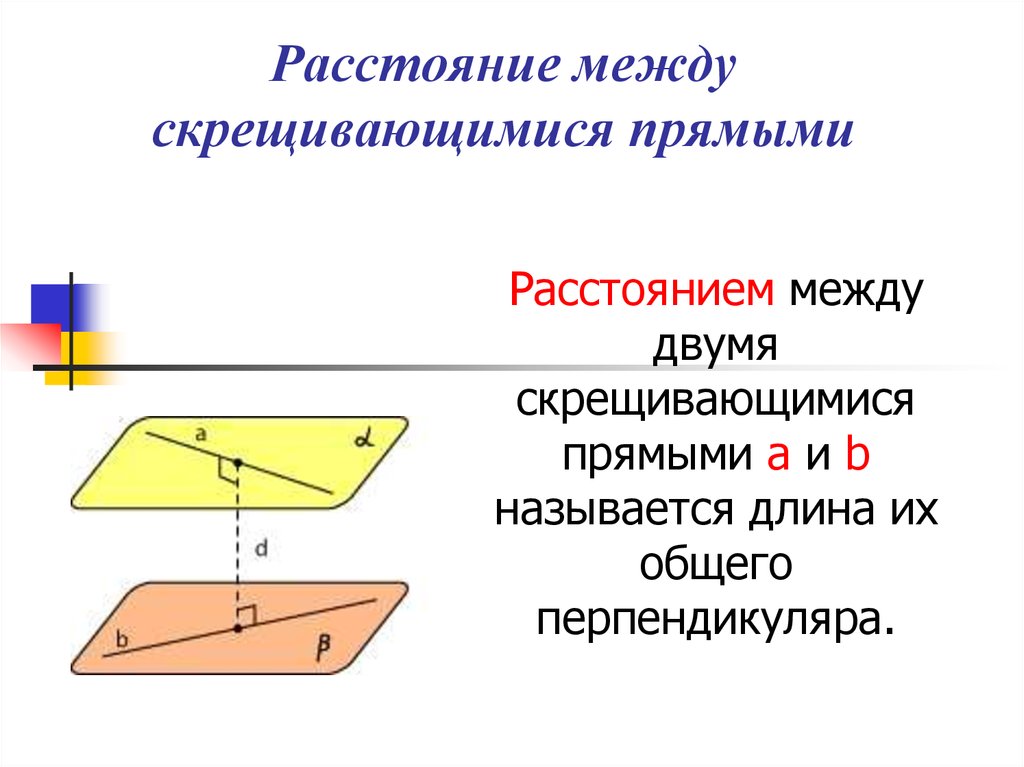
8. Расстояние между скрещивающимися прямыми

Расстоянием между
двумя
скрещивающимися
прямыми а и b
называется длина их
общего
перпендикуляра.

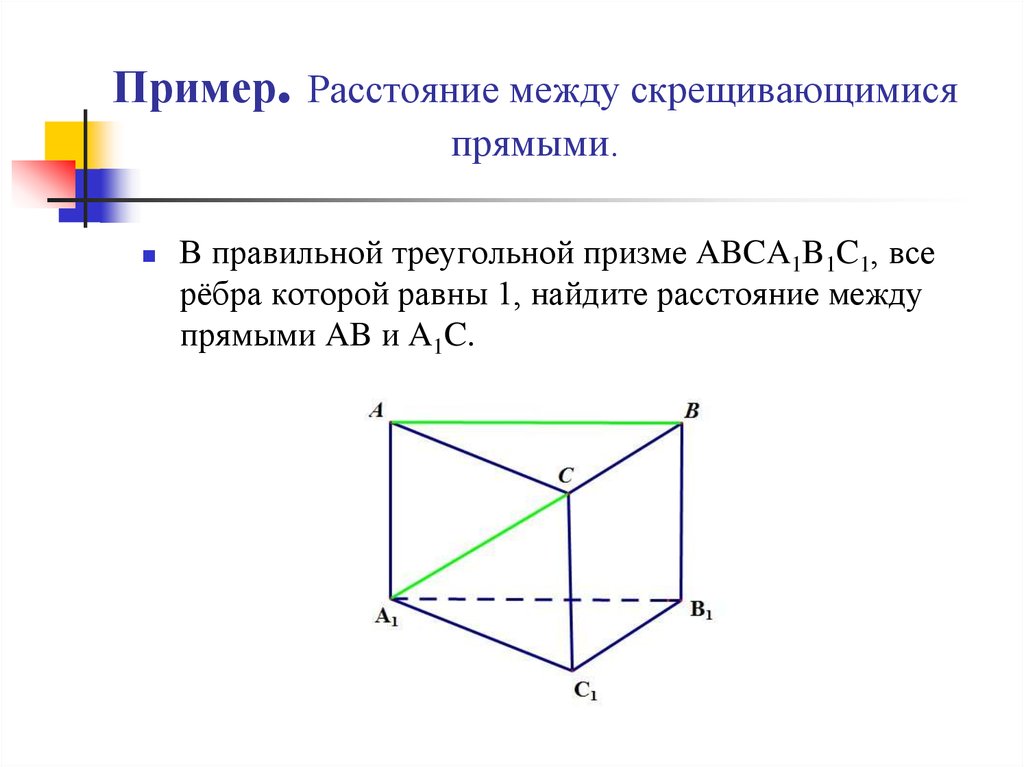
9. Пример. Расстояние между скрещивающимися прямыми.

В правильной треугольной призме ABCA1B1C1, все
рёбра которой равны 1, найдите расстояние между
прямыми AB и A1C.

10. Решение:

(Гиперссылки\3.docx)

11. Угол между скрещивающимися прямыми

За величину угла между скрещивающимися
прямыми a и b принимается величина угла
между параллельными им пересекающимися
в некоторой точке М прямыми a1 и b1, то есть
a; b a1; b1
где a1 | | a и b1 | | b, a1 b1 = {M}

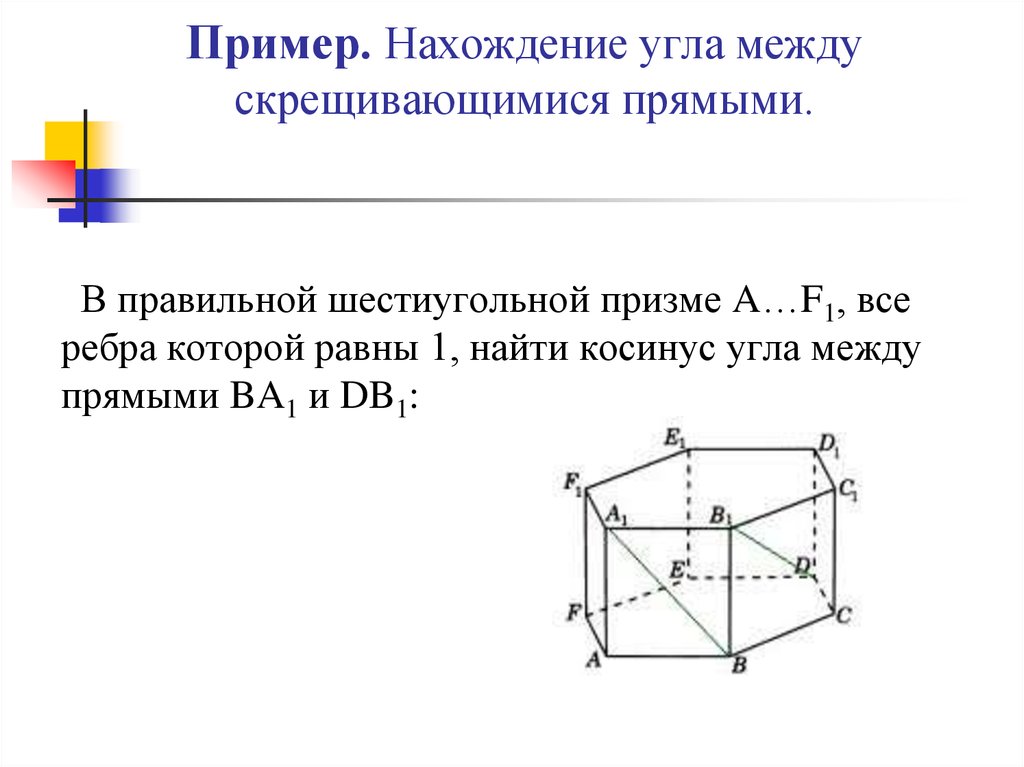
12. Пример. Нахождение угла между скрещивающимися прямыми.

В правильной шестиугольной призме A…F1, все
ребра которой равны 1, найти косинус угла между
прямыми BA1 и DB1:

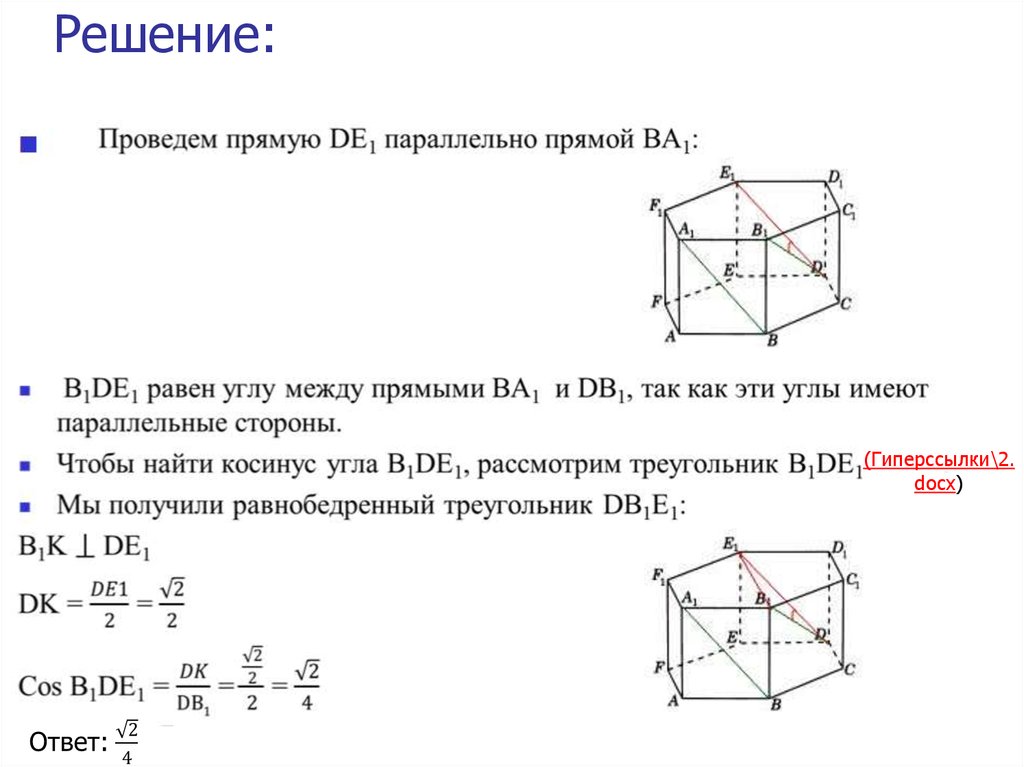
13. Решение:

(Гиперссылки\2.
docx)

14.

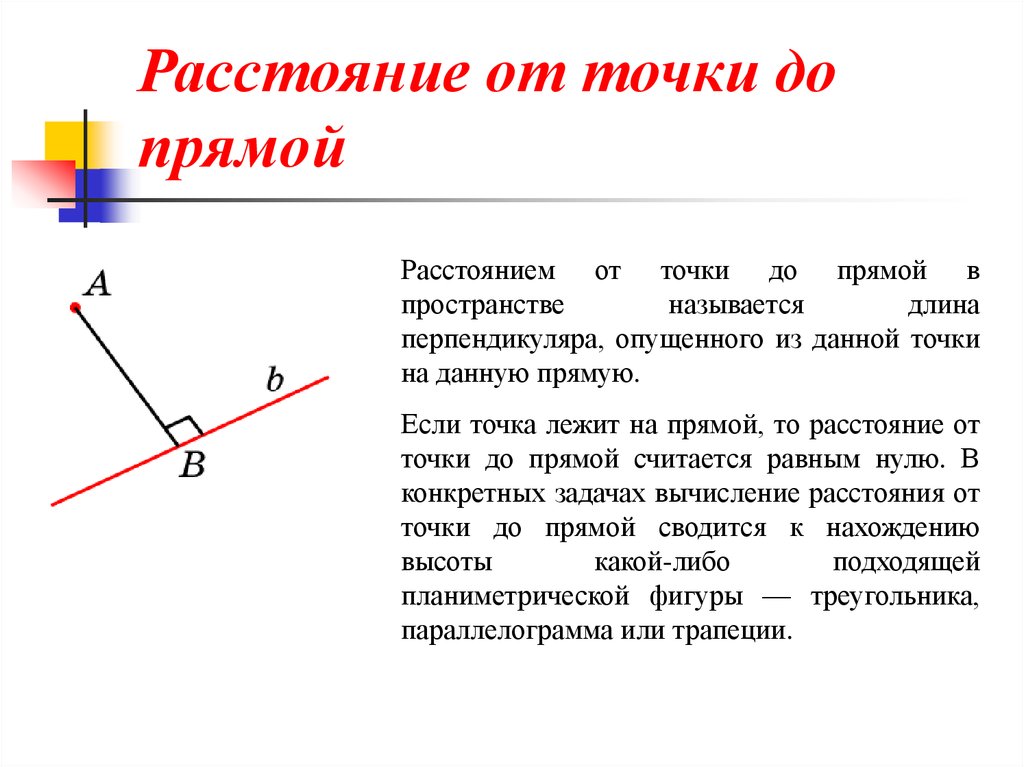
Расстояние от точки до
прямой
Расстоянием от точки до прямой в
пространстве
называется
длина
перпендикуляра, опущенного из данной точки
на данную прямую.
Если точка лежит на прямой, то расстояние от
точки до прямой считается равным нулю. В
конкретных задачах вычисление расстояния от
точки до прямой сводится к нахождению
высоты
какой-либо
подходящей
планиметрической фигуры — треугольника,
параллелограмма или трапеции.

15. Нахождение расстояний 1

Для нахождения расстояния от точки A до прямой l
перпендикуляр AH, опущенный из данной точки на данную
прямую, представляют в качестве высоты треугольника,
одной вершиной которого является точка A, а сторона BC,
противолежащая этой вершине, лежит на прямой l. Зная
стороны этого треугольника, можно найти и его высоту.
При этом возможны следующие случаи:
1. Треугольник ABC – равнобедренный, AB = AC. Пусть AB = AC =
b, BC = a. Искомый перпендикуляр находится из прямоугольного
треугольника ABH:
2
a
2
AH b .
4
H

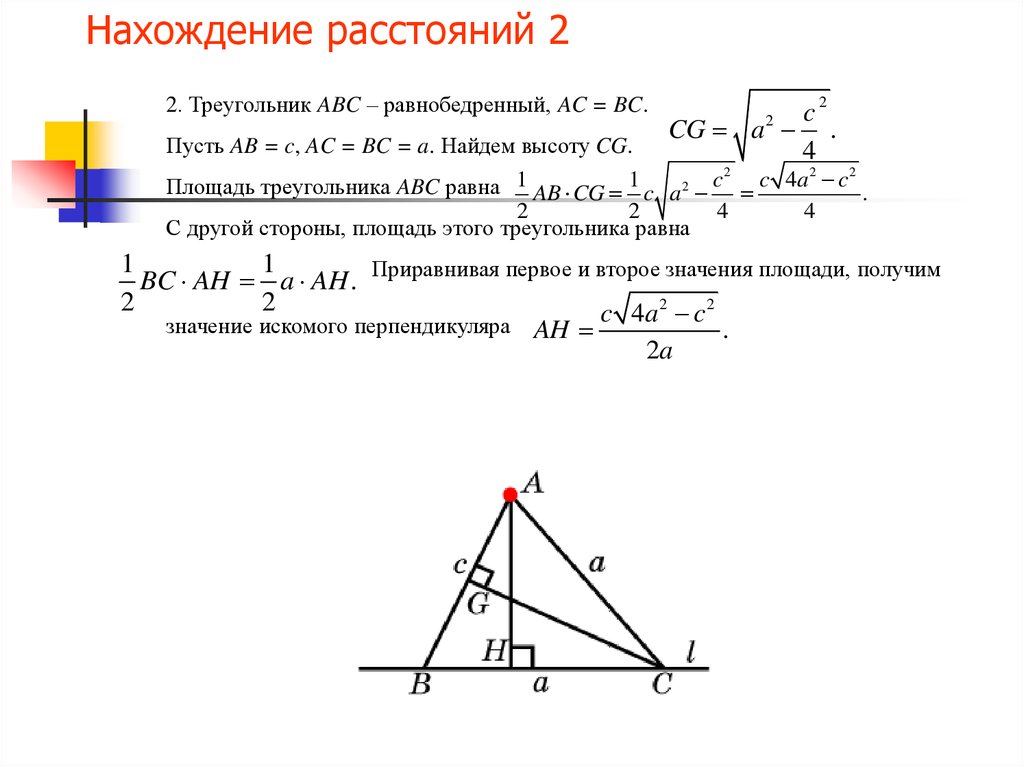
16. Нахождение расстояний 2

2. Треугольник ABC – равнобедренный, AC = BC.
2
c
CG a .
4
2
Пусть AB = c, AC = BC = a. Найдем высоту CG.
2
2
2
Площадь треугольника ABC равна 1 AB CG 1 c a 2 c c 4a c .
2
2
4
4
С другой стороны, площадь этого треугольника равна
1
1
BC AH a AH . Приравнивая первое и второе значения площади, получим
2
2
2
2
c
4
a
c
значение искомого перпендикуляра AH
.
2a

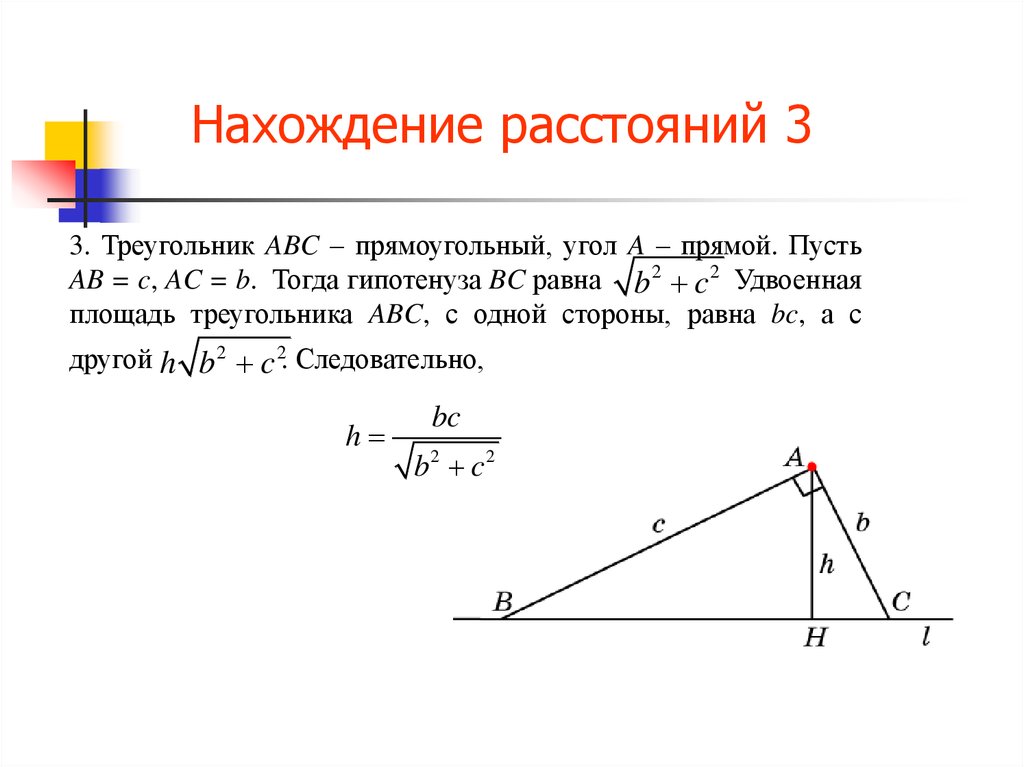
17. Нахождение расстояний 3

3. Треугольник ABC – прямоугольный, угол A – прямой. Пусть
AB = c, AC = b. Тогда гипотенуза BC равна b 2 c 2 Удвоенная
площадь треугольника ABC, с одной стороны, равна bc, а с
другой h b 2 c 2. Следовательно,
h
bc
b2 c2

18. Нахождение расстояний 4

4. Треугольник ABC – произвольный.
Пусть AB = c, AC = b, BC = a, ACB .
По теореме косинусов имеет место равенство c2 a2 b2 2ab cos .
a 2 b2 c 2
Откуда cos
.
2ab
Зная косинус угла, можно найти его синус sin 1 cos 2 ,
а зная синус , можно найти высоту
AH b sin .

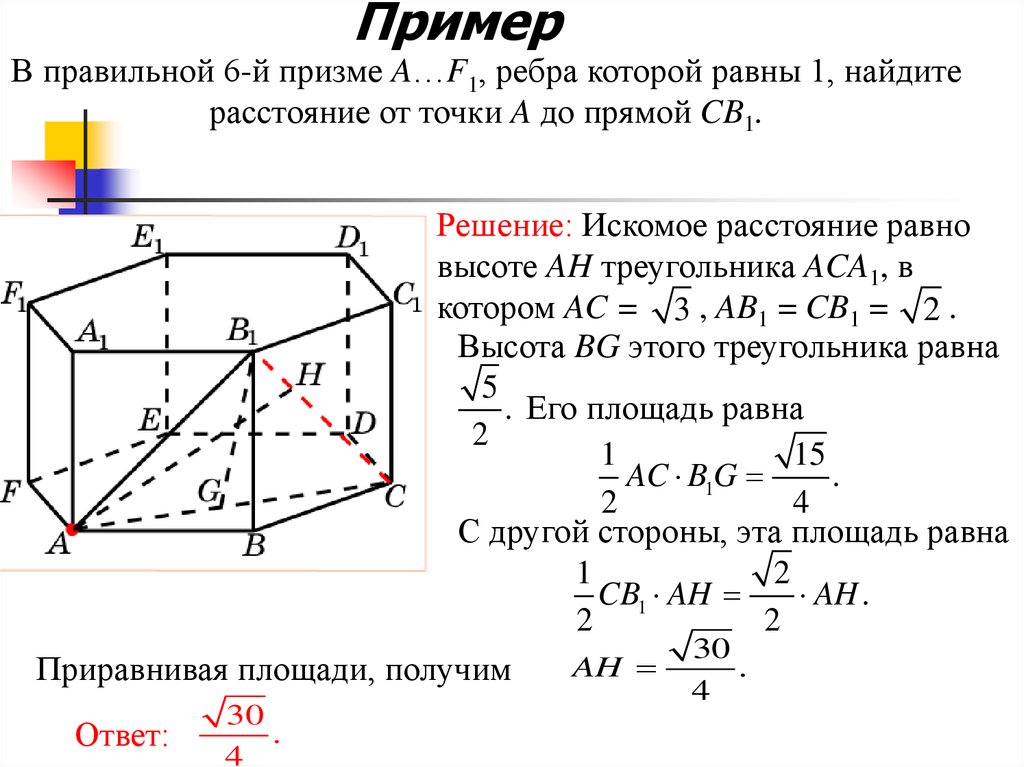
19. Пример

В правильной 6-й призме A…F1, ребра которой равны 1, найдите
расстояние от точки A до прямой CB1.
Решение: Искомое расстояние равно
высоте AH треугольника ACA1, в
котором AC = 3 , AB1 = CB1 = 2 .
Высота BG этого треугольника равна
5
. Его площадь равна
2
1
15
AC B1G
.
2
4
С другой стороны, эта площадь равна
1
2
CB1 AH
AH .
2
2
30
AH
.
Приравнивая площади, получим
Ответ:
30
.
4
4

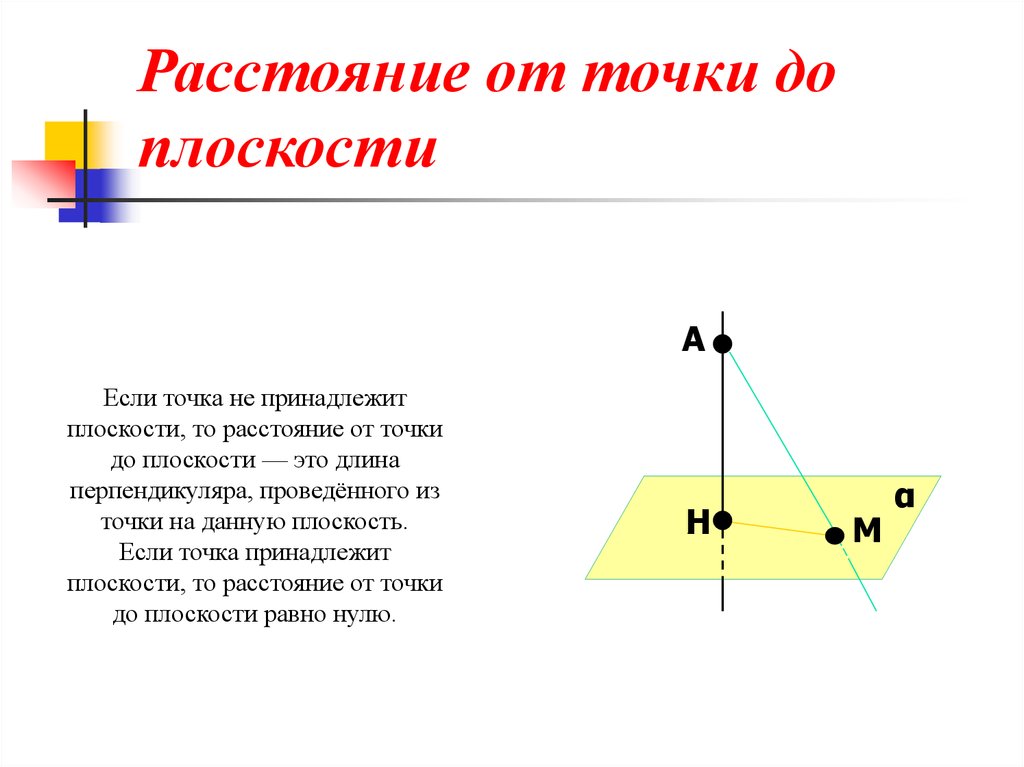
20.

Расстояние от точки до
плоскости
А
Если точка не принадлежит
плоскости, то расстояние от точки
до плоскости — это длина
перпендикуляра, проведённого из
точки на данную плоскость.
Если точка принадлежит
плоскости, то расстояние от точки
до плоскости равно нулю.
Н
М
α

21.

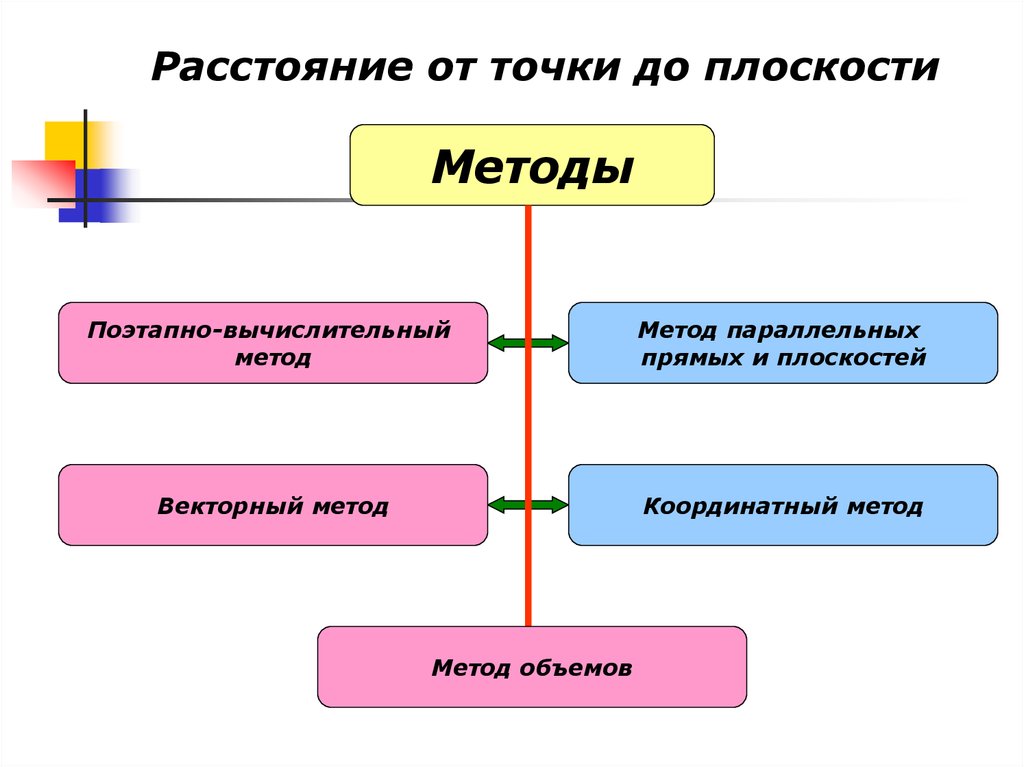
Расстояние от точки до плоскости
Методы
Поэтапно-вычислительный
метод
Метод параллельных
прямых и плоскостей
Векторный метод
Координатный метод
Метод объемов

22.

В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 ,
ребра которой равны 1, найти расстояние от точки А до
плоскости А1В1С.
B1
D1
C1
E1
A1
FC AE, FC AA1 FC ( AA1E1 ).
FC AE G.
( AA1E1 ) ( A1B1C) FC ( A1B1C) ,
( AA1E1 ) ( A1B1C ) AG
1 .
Высота АН в треугольнике АА1G –
искомое расстояние.
F1
Из прямоуг. треугольника ADE:
E
D
H
C
G
F
B
A
Из прямоуг. треугольника AGA1:
3
AE AD ED 3, AG
.
2
2
2
3
7
GA1
1
.
4
2
AG AA1
3
7
3
AH
1:
.
GA1
2
2
7
Ответ:
3
.
7

23.

В единичном кубе ABCDA1B1C1D1 найти расстояние
от точки C1 до плоскости AB1C
A1C1 AC , то AC
1 1
Поэтому искомое расстояние h равно
расстоянию от произвольной точки
А1С1 до плоскости АВ1С.
C1
О1
B1
D1
Обозначим расстояние от О1 до (АВ1С)
через h.
h A1
Е
Покажем, что О1Е ┴ АВ1С.
C
О
B
Так как
AB1C .
A
D
O1E BB1D1D, AC BB1D1D O1E AC
О1Е – перпендикуляр к (АВ1С), а О1Е = h
2
B1O1
, O1O 1, то из прямоугольного треугольника ОВ1О1:
2
1
3 Искомое расстояние: h B1O1 O1O 2 1: 3 3 .
OB1
1
.
OB1
2
2
3
2
2
3
Ответ:
.
3

24.

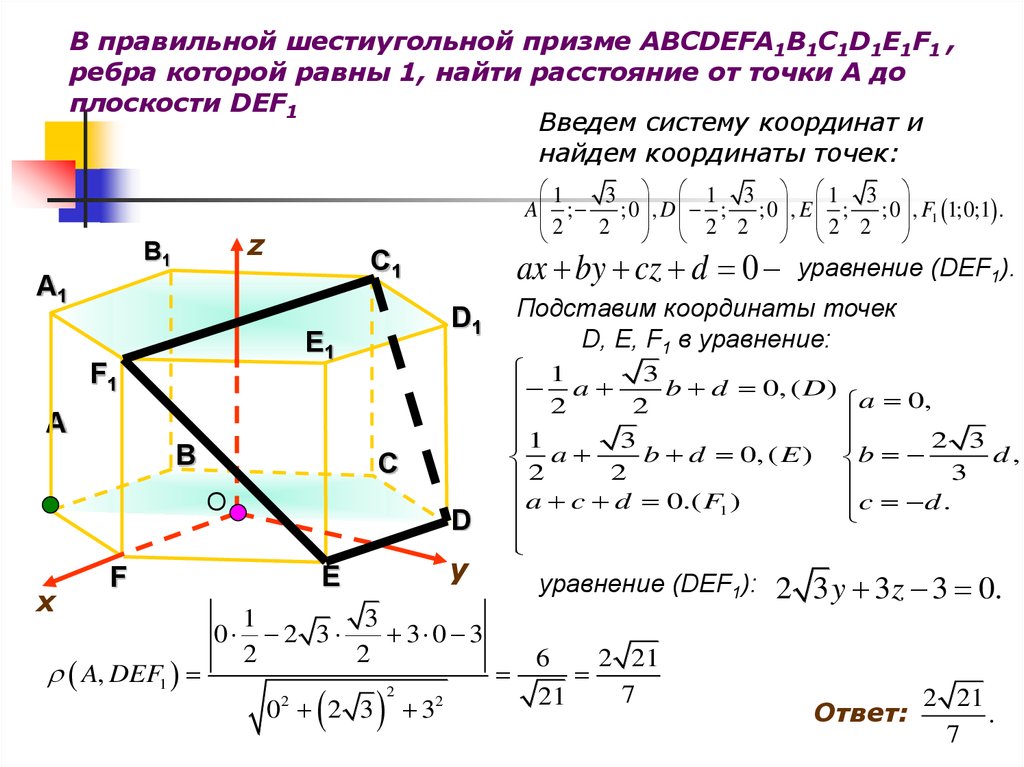
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 ,
ребра которой равны 1, найти расстояние от точки А до
плоскости DEF1
Введем систему координат и
найдем координаты точек:
1
3 1 3 1 3
A ; ;0 , D ; ;0 , E ; ;0 , F1 1;0;1 .
2 2 2 2 2
2
z
B1
ax by cz d 0
C1
A1
F1
A
B
C
O
x
A, DEF1
D
y
E
F
0
1
3
2 3
3 0 3
2
2
02 2 3
Подставим координаты точек
D, E, F1 в уравнение:
D1
E1
2
32
уравнение (DEF1).
1
3
b d 0, ( D )
a
a 0,
2
2
3
2 3
1
b d 0, ( E ) b
d,
a
2
2
3
a c d 0.( F1 )
c d .
уравнение (DEF1):
6
2 21
7
21
2 3 y 3z 3 0.
Ответ:
2 21
.
7

25.

Ребро куба ABCDA1B1C1D1 равно а. Найти расстояние
от точки C до плоскости BDC1
Расстояние х равно высоте CQ, опущенной
в пирамиде BCDC1 из вершины С на
основание BDC1
B1
A1
C1
D1
1
1 1
a3
V1 S BCD CC1 BC CD CC1 .
3
3 2
6
Треугольник BDC1 – равносторонний.
Q
B
C
A
R
2
1
1 a 2 3
a2 3
V2 S BC1D CQ
x
x.
3
3
4
6
D
Так как V1 = V2, то получаем уравнение:
a3
a2 3
a 3
x; x
.
6
6
3
Ответ:
a 3
.
3

26. Метод координат

27. Главные формулы

1. Косинус угла φ между векторами a = (x1; y1; z1) и
b = (x2; y2; z2):
2. Уравнение плоскости в трехмерном пространстве:
Ax + By + Cz + D = 0, где A, B, C и D — действительные числа,
причем, если плоскость проходит через начало координат, D = 0.
А если не проходит, то D = 1.
3. Вектор, перпендикулярный к плоскости (нормаль)
Ax + By + Cz + D = 0, имеет координаты: n = (A; B; C).

28.

4.Координаты середины отрезка
Итак, пусть отрезок задан своими концами —
точками A = (xa; ya; za) и B = (xb; yb; zb). Тогда координаты середины
отрезка — обозначим ее точкой H — можно найти по формуле:
5. Расстояние от точки до плоскости:

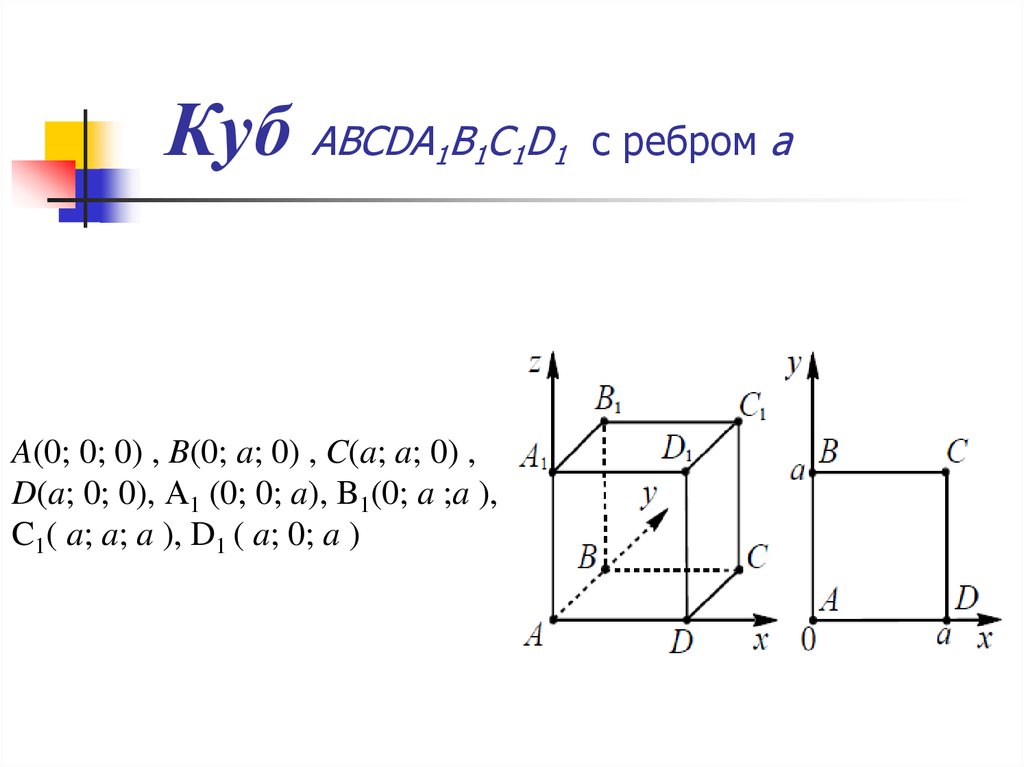
29. Куб ABCDA1B1C1D1 с ребром a

Куб ABCDA B C D
1 1 1 1
A(0; 0; 0) , B(0; a; 0) , C(a; a; 0) ,
D(a; 0; 0), А1 (0; 0; a), B1(0; a ;a ),
C1( a; a; a ), D1 ( a; 0; a )
с ребром a

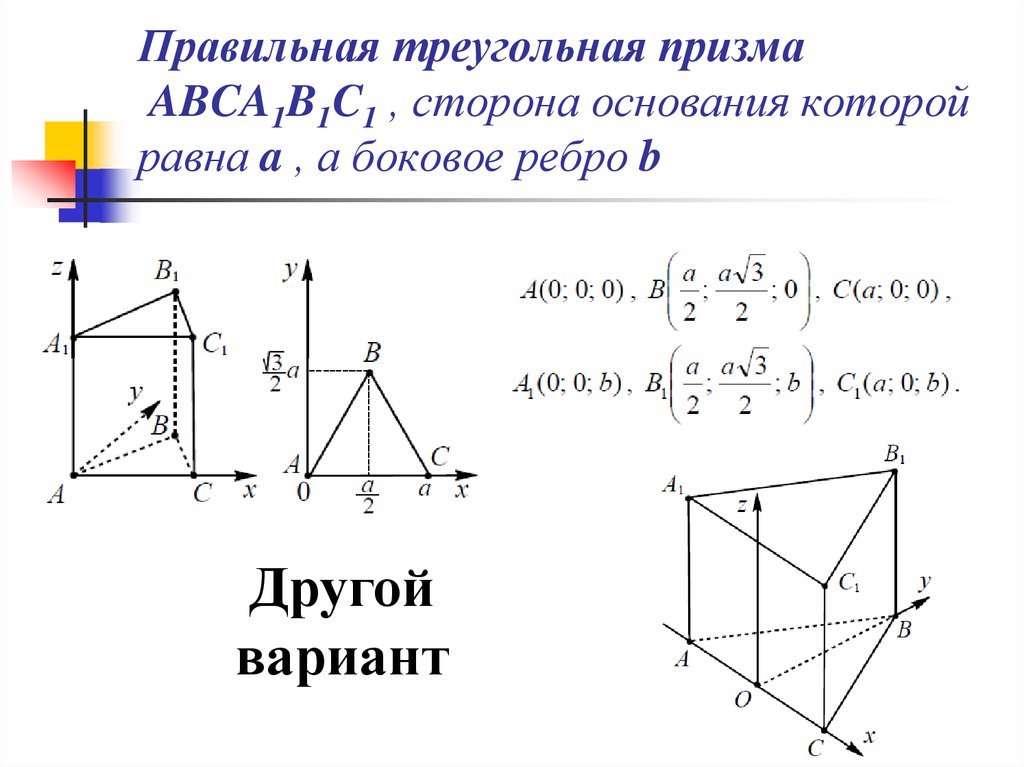
30. Правильная треугольная призма ABCA1B1C1 , сторона основания которой равна a , а боковое ребро b

Другой
вариант

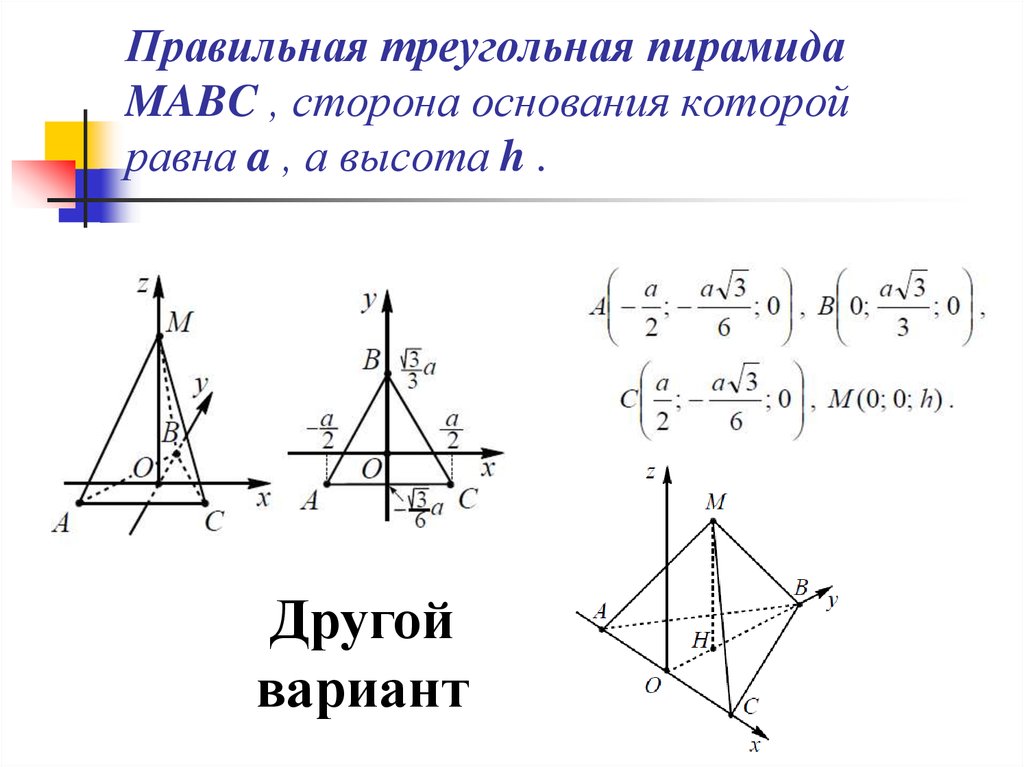
31. Правильная треугольная пирамида MABC , сторона основания которой равна a , а высота h .

Другой
вариант

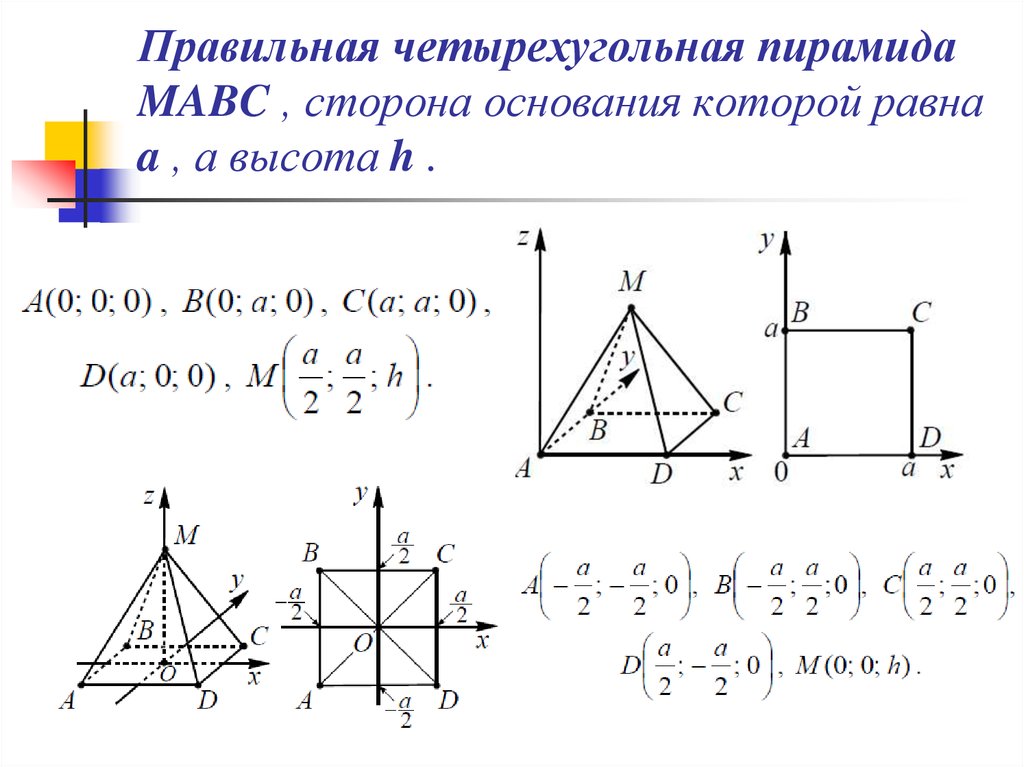
32. Правильная четырехугольная пирамида MABC , сторона основания которой равна a , а высота h .

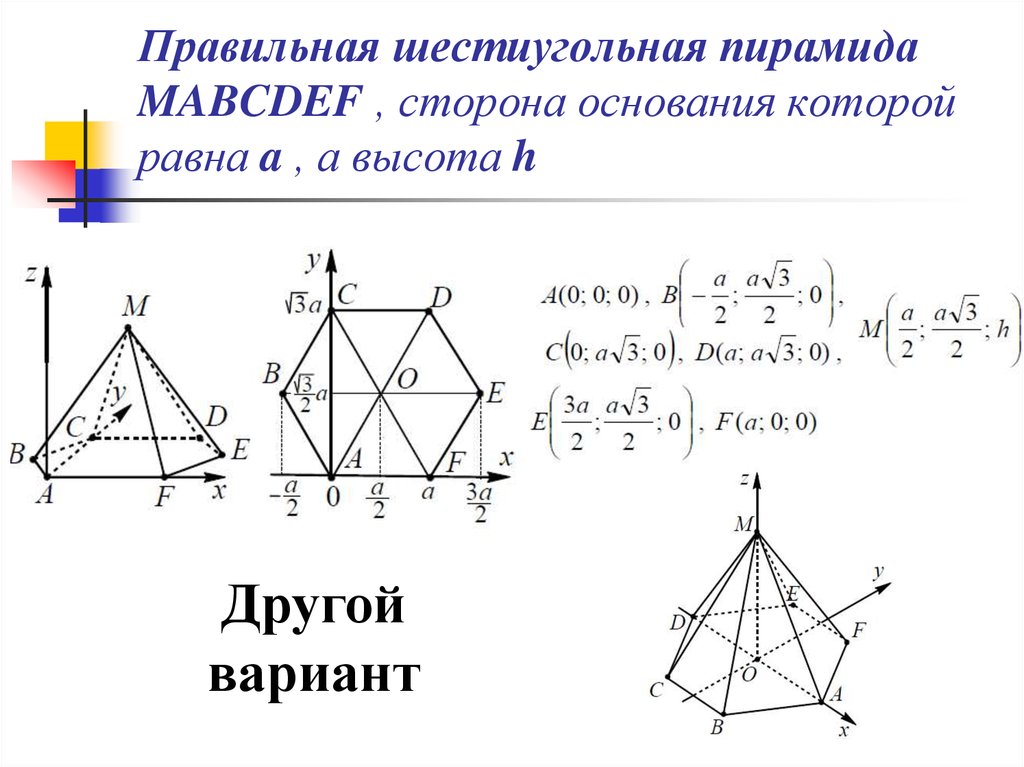
33. Правильная шестиугольная пирамида MABCDEF , сторона основания которой равна a , а высота h

Другой
вариант

34. Пример

Пример

35. Пример 2. Точка E — се­ре­ди­на ребра CC1 куба ABCDA1B1C1D1. Най­ди­те угол между пря­мы­ми BE и AD.

Пример 2. Точка E — середина
ребра CC1 куба ABCDA1B1C1D1. Найдите угол между
прямыми BE и AD.
1. Вводим систему координат с началом в точке D(0; 0; 0).
2. Примем сторону куба за единицу. Координаты точек:
A (1; 0; 0);
D (0; 0; 0);
B (1; 1; 0);
E (0; 1; 0,5).
3. Тогда
AD {-1; 0; 0};
BE {-1; 0; 0,5};
4. cos α =
│−1∗ −1 +0+0│
1+0+0+ 1+0+0,25
=
2
5
=
2 5
.
5
Отсюда
α = arccos
2 5
.
5
Ответ: α = arccos
2 5
.
5

36. Сечения

37.

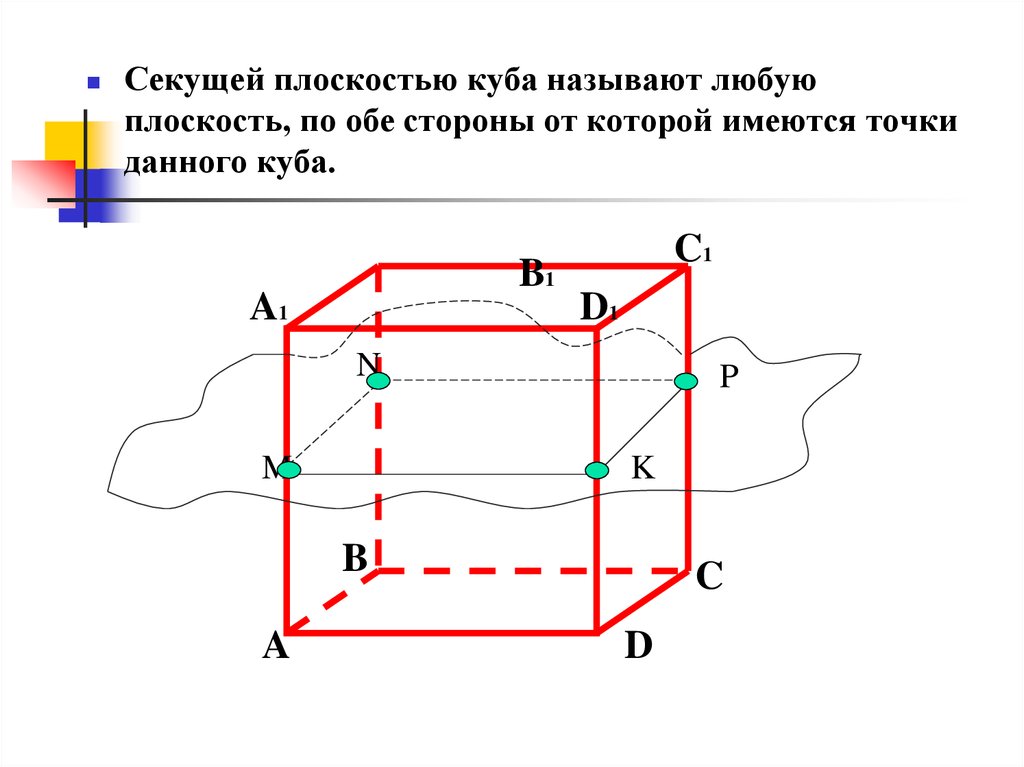
Секущей плоскостью куба называют любую
плоскость, по обе стороны от которой имеются точки
данного куба.
B1
A1
C1
D1
N
M
P
K
B
A
C
D

38.

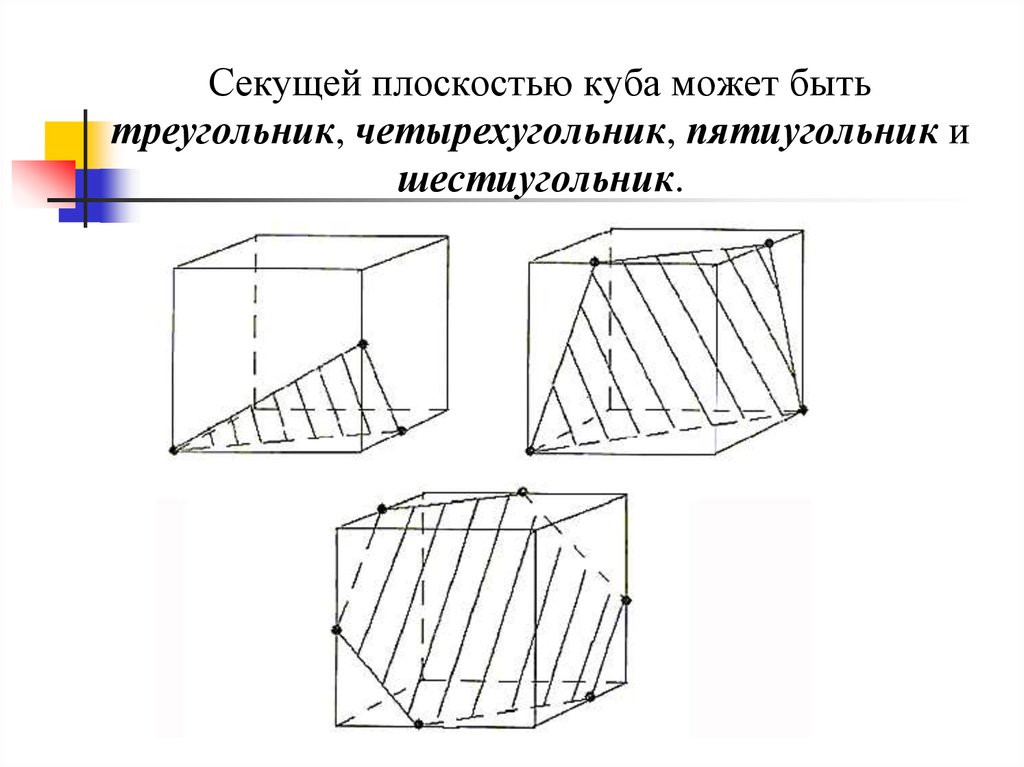
Секущей плоскостью куба может быть
треугольник, четырехугольник, пятиугольник и
шестиугольник.

39. Пример.

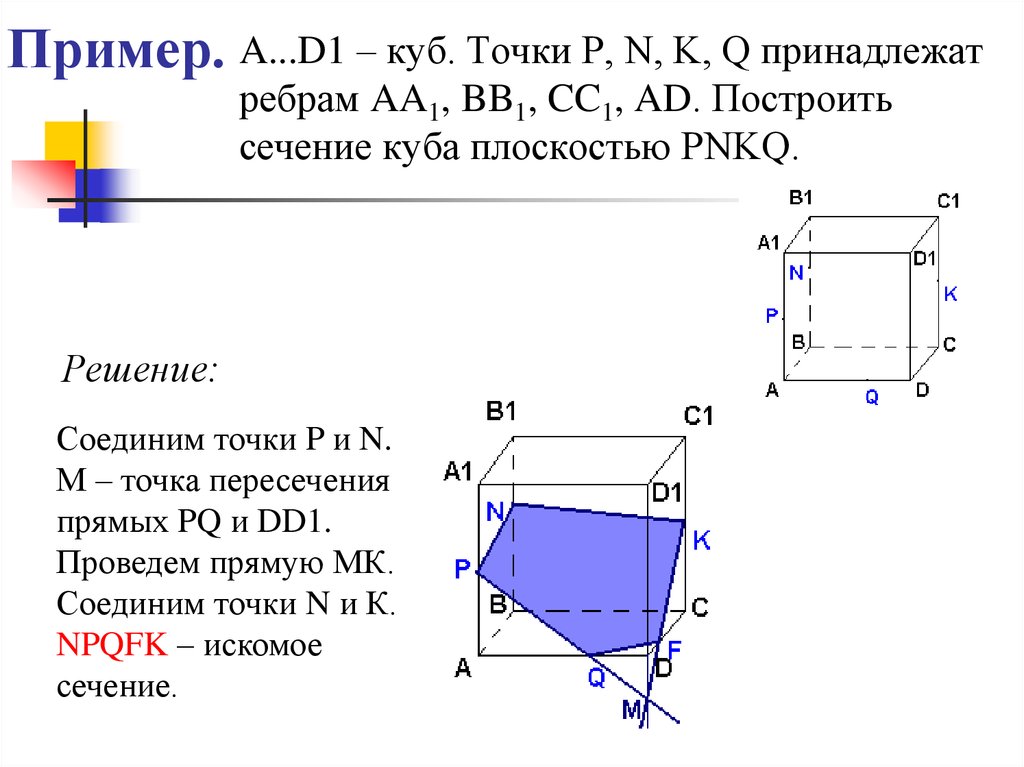
A...D1 – куб. Точки P, N, K, Q принадлежат
ребрам AA1, BB1, CC1, AD. Построить
сечение куба плоскостью PNKQ.
Решение:
Соединим точки P и N.
М – точка пересечения
прямых PQ и DD1.
Проведем прямую МК.
Соединим точки N и К.
NPQFK – искомое
сечение.

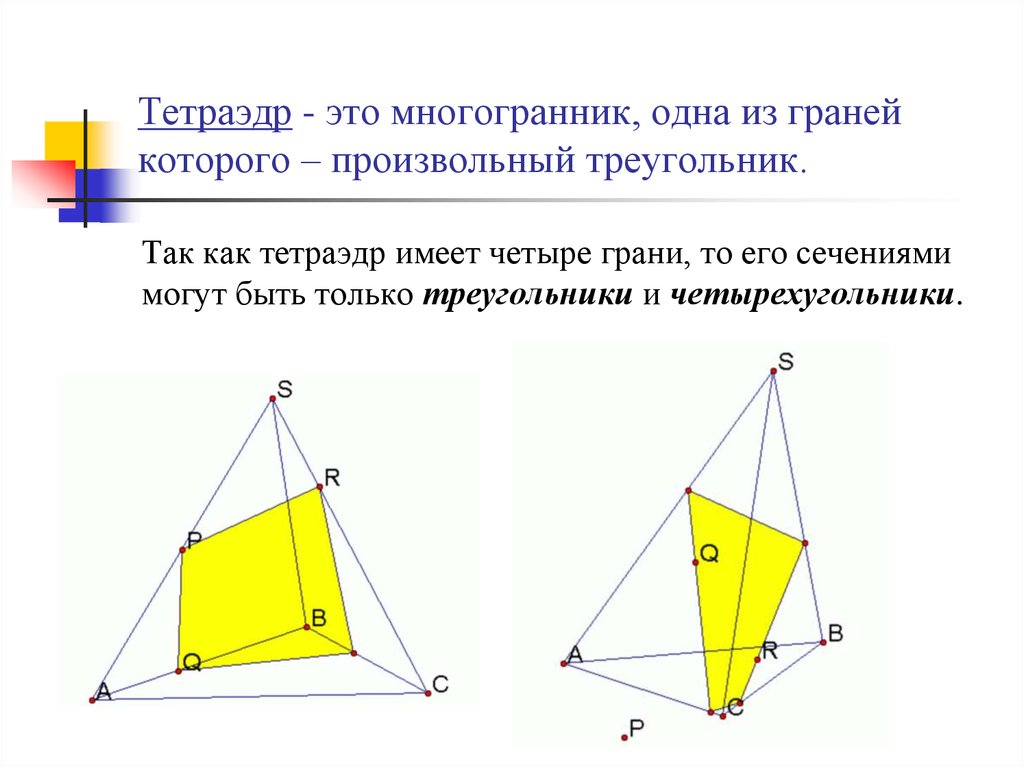
40. Тетраэдр - это многогранник, одна из граней которого – произвольный треугольник.

Так как тетраэдр имеет четыре грани, то его сечениями
могут быть только треугольники и четырехугольники.

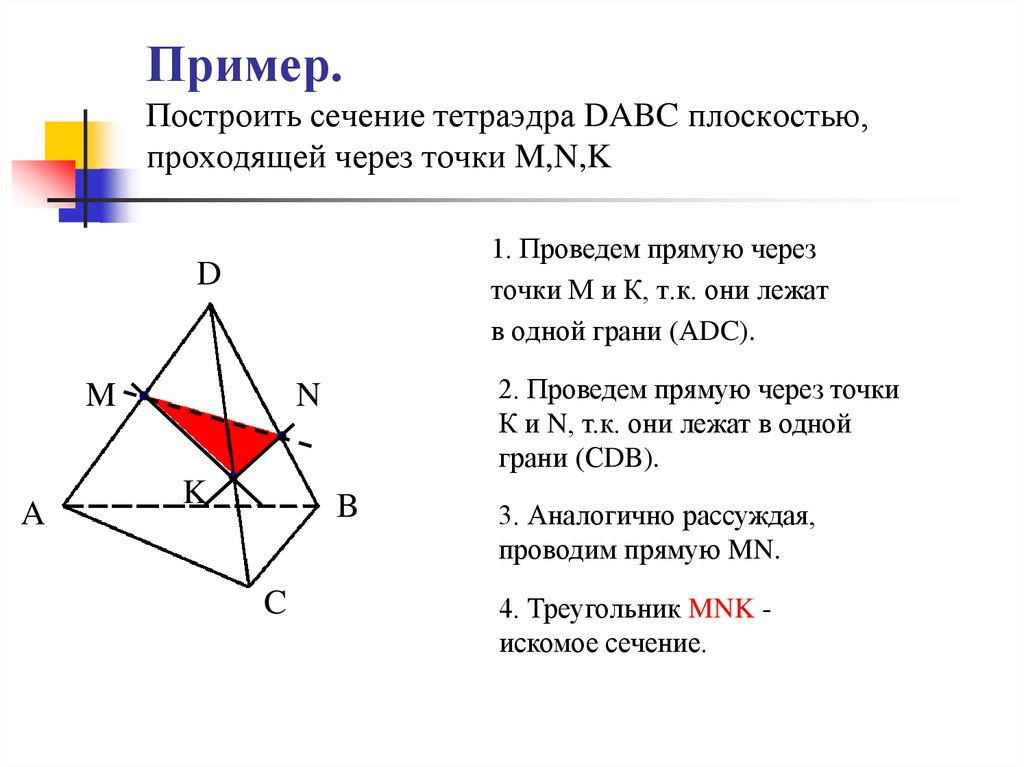
41. Пример. Построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K

1. Проведем прямую через
точки М и К, т.к. они лежат
в одной грани (АDC).
D
M
AA
2. Проведем прямую через точки
К и N, т.к. они лежат в одной
грани (СDB).
N
K
BB
C
C
3. Аналогично рассуждая,
проводим прямую MN.
4. Треугольник MNK искомое сечение.

42.

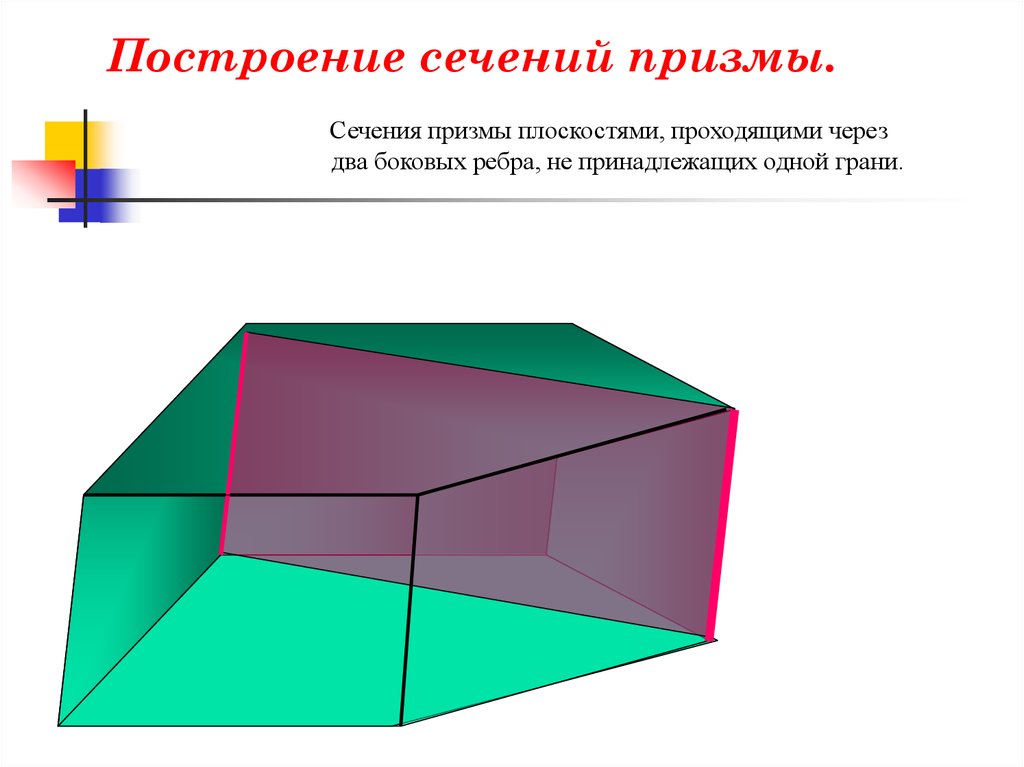
Построение сечений призмы.
Сечения призмы плоскостями, проходящими через
два боковых ребра, не принадлежащих одной грани.

43.

Построение сечения призмы плоскостями,
параллельными боковому ребру.

44.

Построение сечения призмы плоскостью,
проходящей через след секущей плоскости.
g

45.

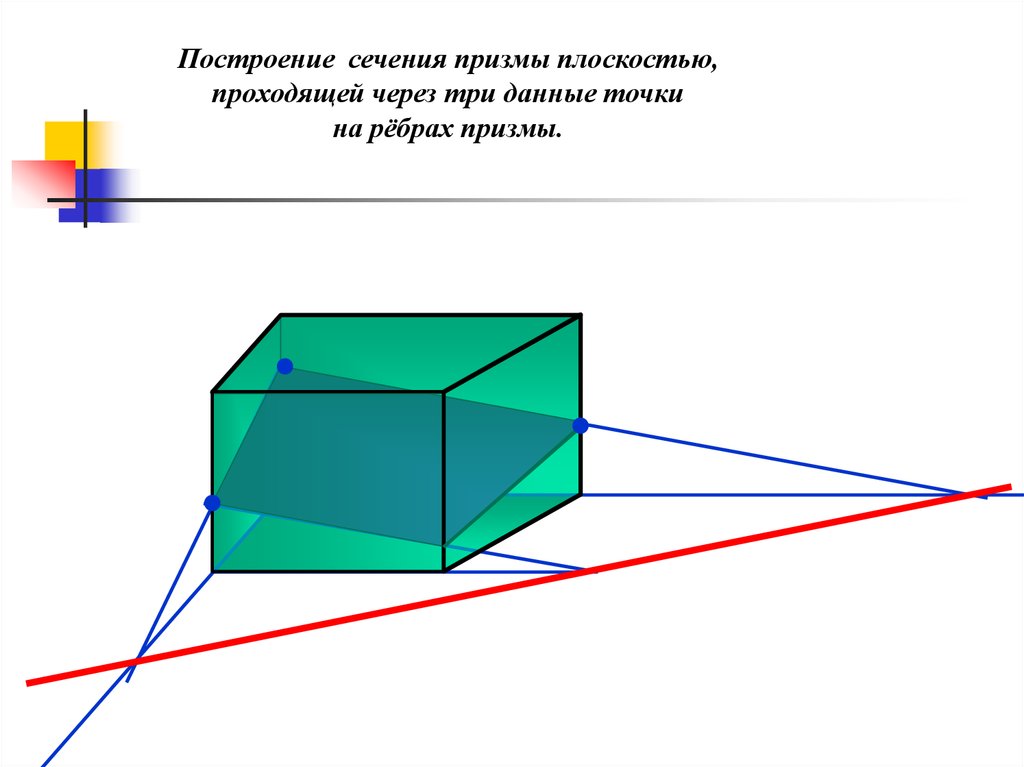
Построение сечения призмы плоскостью,
проходящей через три данные точки
на рёбрах призмы.

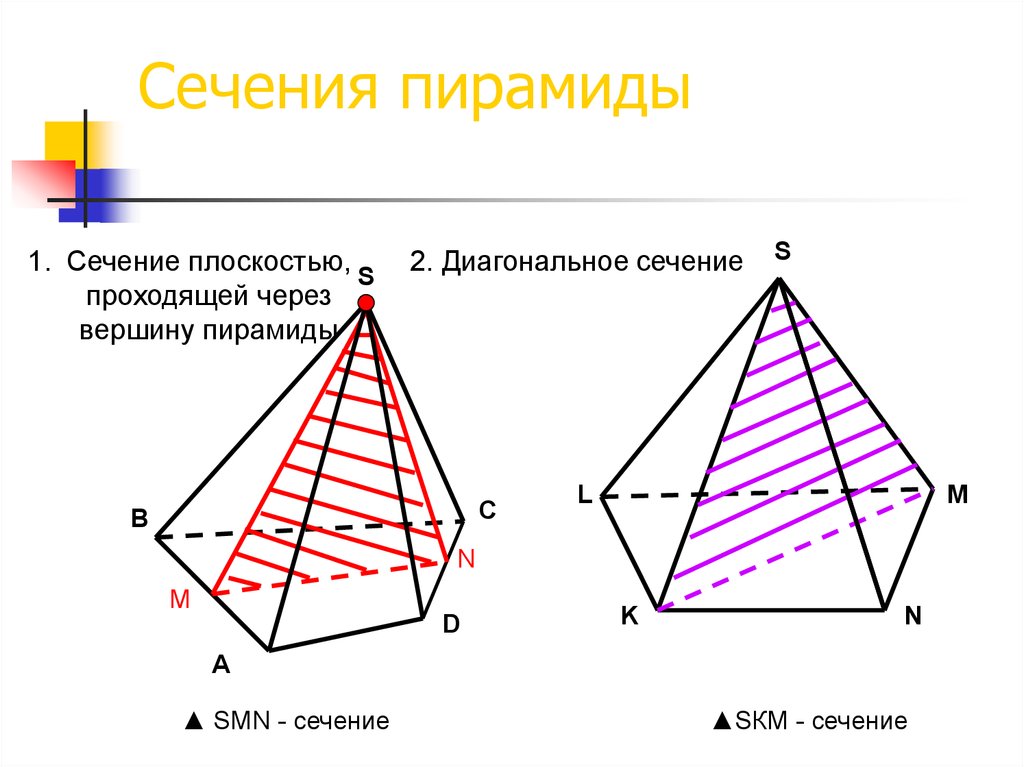
46. Сечения пирамиды

1. Сечение плоскостью,
S
проходящей через
вершину пирамиды
2. Диагональное сечение
С
В
S
L
M
N
M
D
K
N
А
▲ SMN - сечение
▲SКM - сечение

47.

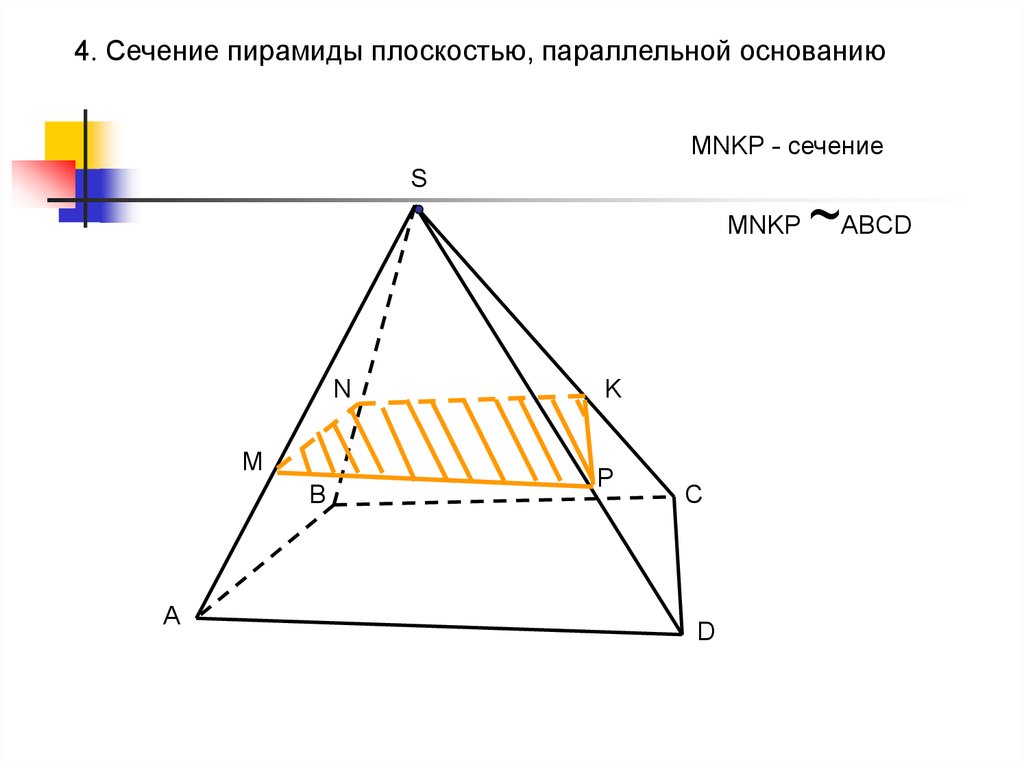
4. Сечение пирамиды плоскостью, параллельной основанию
MNKP - сечение
S
MNKP
N
M
B
A
K
P
C
D
~ABCD

48.

Построить сечение плоскостью, проходящей через точки M, P и K.
S
R
M
B
C
T
N
P
MPKNR - сечение
D
A
K
L

49. Пример

В правильной треугольной призме стороны
основания равны 6, боковые рёбра равны 4.
Изобразите сечение, проходящее через вершины и
середину ребра. Найдите его площадь.