Похожие презентации:
Решение задач по готовым чертежам
1. РЕШЕНИЕ ЗАДАЧ ПО ГОТОВЫМ ЧЕРТЕЖАМ
2. ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ
3.
4. Необходимые формулы и теоремы
Площадь треугольника (в зависимости от заданных условий) можно
вычислить по формулам
1
1
1
S ab
S
ah
S ab sin
2
2
2
Площадь боковой поверхности правильной пирамиды:
Объем пирамиды V=1/3 SоснH
Медианы в треугольнике точкой пересечения делятся в отношении 2:1
начиная от вершины
Площадь квадрата или ромба S=1/2d1d2.
Площадь ромба, параллелограмма S=ah
Радиус окружности описанной около треугольника можно вычислить по
abc
формуле
R
4S
Центр окружности,описанной около прямоугольного треугольника,
расположен в середине гипотенузы
№1
№2
№3
№4
№5
№6
№7
5. Угол между боковым ребром и основанием правильной пирамиды
Углом между боковым ребромправильной пирамиды и
основанием пирамиды называется
угол между боковым ребром и его
проекцией на основание.
В правильной пирамиде углы между
боковыми рёбрами и основанием
равны между собой.
На данном чертеже углы выделены
фиолетовым цветом
6. Угол между боковой гранью и основанием правильной пирамиды
Углом между боковой граньюправильной пирамиды и
основанием пирамиды является
угол между апофемой
правильной пирамиды и её
проекцией на основание.
В правильной пирамиде углы
между боковыми гранями и
основанием равны между собой.
На данном чертеже углы
выделены дужкой серого цвета
7. Задача №1
• Сторона основания правильнойтреугольной пирамиды ABCD равна 3, а
боковое ребро пирамиды AD=2 3. Найдите
объем пирамиды.
Пояснения:
При выполнении чертежа пирамиды не забывайте, что у правильной
пирамиды её вершина проектируется в центр основания.
Центром правильного треугольника является точка пересечения
медиан треугольника (достаточно изобразить 2 медианы).
Медиана – отрезок, выходящий из вершины треугольника, делящий
противоположную сторону пополам
Чертёж пирамиды всегда начинаем с основания- треугольника ABC;
Определяем точку О– центр треугольника; Восстанавливаем
перпендикуляр (высоту пирамиды) OD из центра треугольника;
Выполняем чертежи боковых рёбер DA, DB, DC. Чертёж пирамиды
готов.
.
8.
№1Дано: DABC- правильная пирамида
АВ=3, AD=2 3
D
Найти:V
2 3
Решение:
3
О
А
N
М
В
1. Учтите, что в основании равносторонний
треугольник. Найдите площадь
основания.
Из треугольника АМС найдите медиану МС.
С 2.
3. Вспомните свойство точки пересечения
медиан. Найдите длину ОС.
4. Из треугольника DOC найдите высоту
пирамиды DO.
5. Найдите объем пирамиды.
Предложите свое решение.
9.
№2FABCD- правильная пирамида,
боковые рёбра наклонены к
основанию под углом 45º, высота
пирамиды равна 2
Дано: FABCD- правильная
пирамида, FCO=45º, FO=2
Найти: V
F
2
C
C
План решения:
B
O
A
D
1.Определите вид треугольника FOC и его углы.
Сделайте вывод о длине ОС.
2. Найдите АС.
3.Вспомните формулу для нахождения площади
квадрата по его диагоналям. Найдите площадь
основания.
4.Вычислите объем пирамиды по формуле V=1/3SоснH
Предложите свое решение.
10.
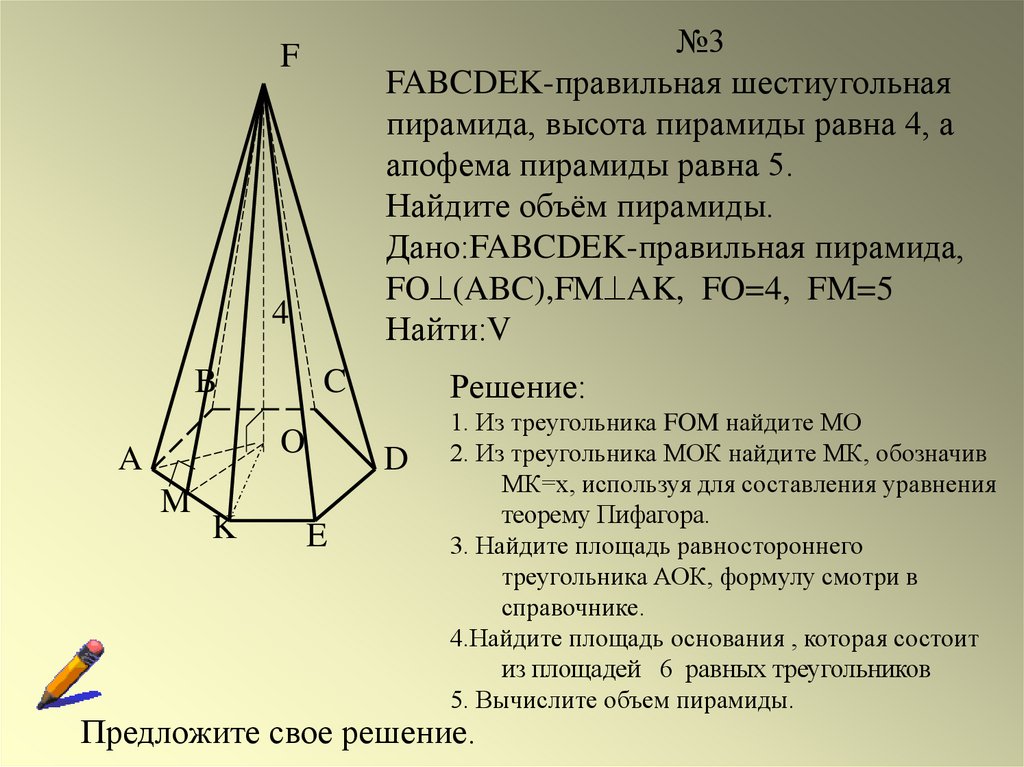
№3FABCDEK-правильная шестиугольная
пирамида, высота пирамиды равна 4, а
апофема пирамиды равна 5.
Найдите объём пирамиды.
Дано:FABCDEK-правильная пирамида,
FO (ABC),FМ AK, FO=4, FM=5
Найти:V
F
4
B
O
A
M
K
Решение:
C
D
E
1. Из треугольника FOM найдите МО
2. Из треугольника МОК найдите МК, обозначив
МК=х, используя для составления уравнения
теорему Пифагора.
3. Найдите площадь равностороннего
треугольника АОК, формулу смотри в
справочнике.
4.Найдите площадь основания , которая состоит
из площадей 6 равных треугольников
5. Вычислите объем пирамиды.
Предложите свое решение.
11.
№4DABC- пирамида, основанием которой служит
прямоугольный треугольник АВС с гипотенузой АВ,
катеты треугольника равны 6 и 8 см. Каждое боковое
ребро наклонено к плоскости основания под углом 45о
Найдите объём пирамиды.
D
Дано: DABC- пирамида, треугольник АВС
прямоугольный, АВ-гипотенуза
АС=6, DCO= DBO= DAO=45º Найти: V
В
О
А
8
6
С
Предложите свое решение
План решения:
1. Вспомните, где расположен центр окружности
т. О, описанной около прямоугольного
треугольника АВС.
Точка О является основанием высоты пирамиды.
Поэтому угол наклона каждого ребра
DCO= DBO= DAO=45º.
2 . Найдите площадь прямоугольного треугольника
АВС по известным катетам.
3.Из прямоугольного треугольника АВС найдите
гипотенузу АВ и отрезок ОВ.
4..Определите вид треугольника DOB и его углы.
Точка О является основанием высоты
пирамиды. Сделайте вывод о длине ОD.
5.Вычислите объем пирамиды.










 Математика
Математика








