Прямоугольные треугольники. Решение задач по готовым чертежам

1.

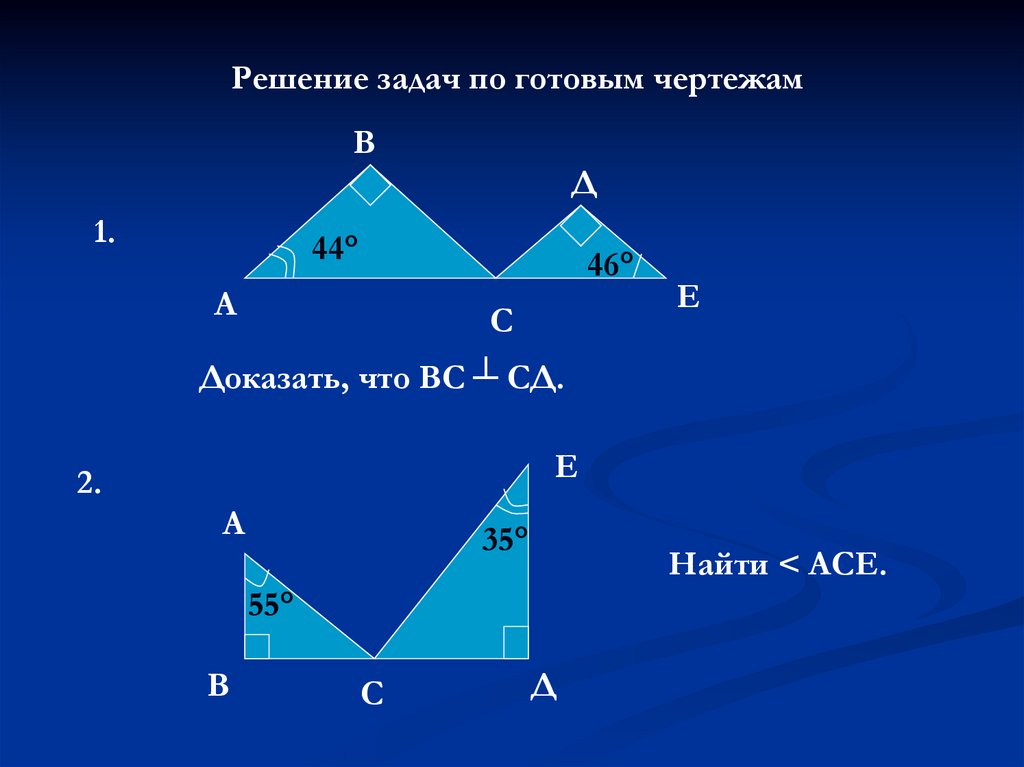
Решение задач по готовым чертежам
В
Д
1.
44°
46°
А
С
Е
Доказать, что ВС ┴ СД.
Е
2.
А
35°
Найти < АСЕ.
55°
В
С
Д

2.

3.
В
60°
Дано: ВН = 4см.
Н
Найти: АН.
А
С
4.
С
Д
О
47°
А
В
Дано: АВ // СД. Найти: углы Δ ДСО.

3.

5.
А
С
О
Д
В
Дано: О – общая середина АВ и СД, АВ ┴ СД.
Доказать: АС = ДВ.

4.

М
6.
А
В
К
С
N
Доказать: МС – медиана Δ КМN.
В
Дано: ВД – биссектриса < АВС.
7.
Доказать: ДВ – биссектриса
С
А
Д
< АДС.

5.

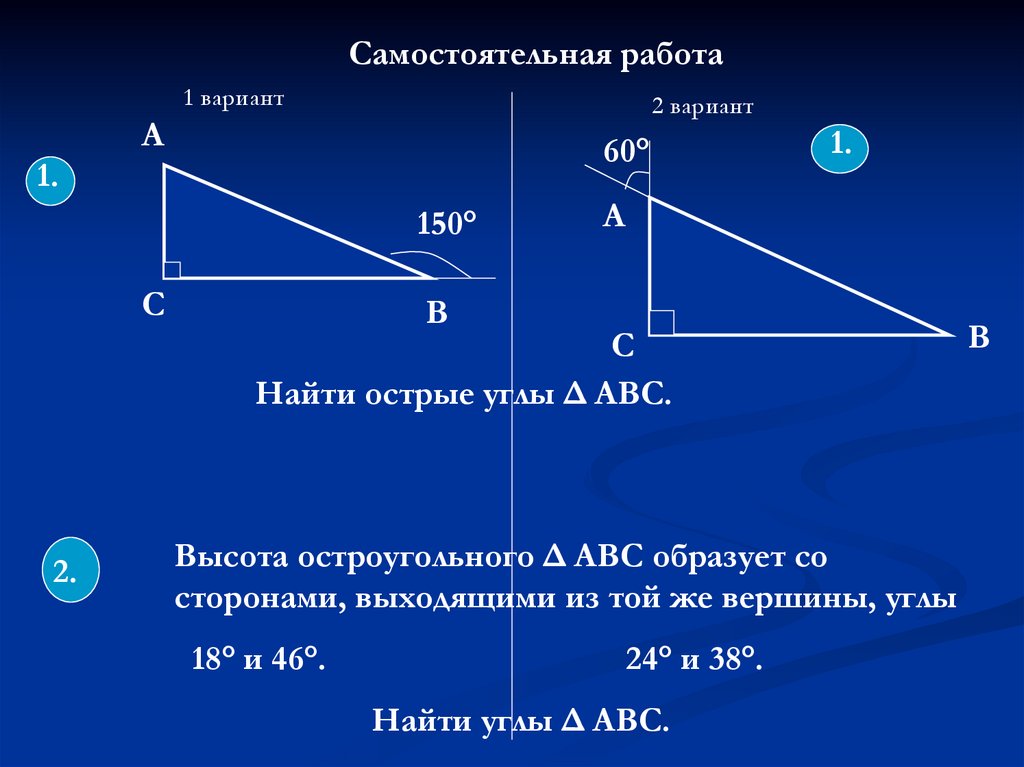
Самостоятельная работа
1 вариант
2 вариант
А
60°
1.
150°
С
1.
А
В
С
Найти острые углы Δ АВС.
2.
Высота остроугольного Δ АВС образует со
сторонами, выходящими из той же вершины, углы
18° и 46°.
24° и 38°.
Найти углы Δ АВС.
В

6.

В
<1=<2,
Е
60°
1
ВМ=5 см.
2
С
М
А
Найти: МЕ.
А
Д
< ДСВ = 50°.
Найти: < А, < В.
С
В

7.

Д /з. § 37, вопросы 14 – 18 изучить
самостоятельно.

8.

А
1.
Самостоятельная работа.
А
1.
150°
С
Д
В
110°
С
Д
В
Дано: АД –биссектриса
угла А.
Дано: АД –биссектриса
угла А.
Найти: острые углы
Найти: острые углы
Δ АДС
Δ АВС.

9.

2.
Биссектриса прямого
угла прямоугольного
треугольника образует
с гипотенузой углы,
один из которых равен
70°.
Найдите острые углы
этого треугольника.
2.
Высота прямоугольного
треугольника, опущенная
на гипотенузу, образует с
одним из катетов угол 55°.
Найдите острые углы
этого треугольника

10.

№ 270.
В
А
О
С
Пусть В и С - искомые
точки, т.е. ОВ =ОС, тогда
Δ ОВС – равнобедренный,
а точка А принадлежит его
основанию ВС.
Биссектриса ОК данного
треугольника является его
высотой, т. е. ОК ┴ ВС.
В
Построение:
А
К
О
С

11.

1. Строим биссектрису угла О – ОК.
2. Строим перпендикуляр к прямой ОК,
проходящий через точку А.
3. Перпендикуляр пересекает стороны угла в точках
В и С. ВС – искомая прямая.
Доказательство: прямоугольные треугольники ОВК
и ОСК равны по катету и острому углу, тогда
ОВ = ОС.