Понятие пирамиды

1.

• А1А2А3 … Аn - основание
S
• А1S, А2S, А3S, … АnS –
боковые ребра
• S – вершина
Аn
А1
Аn-1
А4
Н
А2
А3
• боковые грани
• SH – высота
• S А1А2А3 … Аn –
обозначение пирамиды

2.

3.

П
И
Р
А
М
И
Д
Ы
Неправильная пирамида
Правильная пирамида

4.

Правильная пирамида
Пирамида называется правильной, если в
основании – правильный многоугольник, а
отрезок соединяющий вершину с центром
основания является высотой.

5.

6.

D
А
О
В
С
ΔABC – правильный;
О – точка
пересечения
медиан (высот
и биссектрис),
центр вписанной
и описанной
окружностей.

7.

S
C
D
Н
О
А
В
ABCD –
квадрат;
О – точка
пересечения
диагоналей.

8.

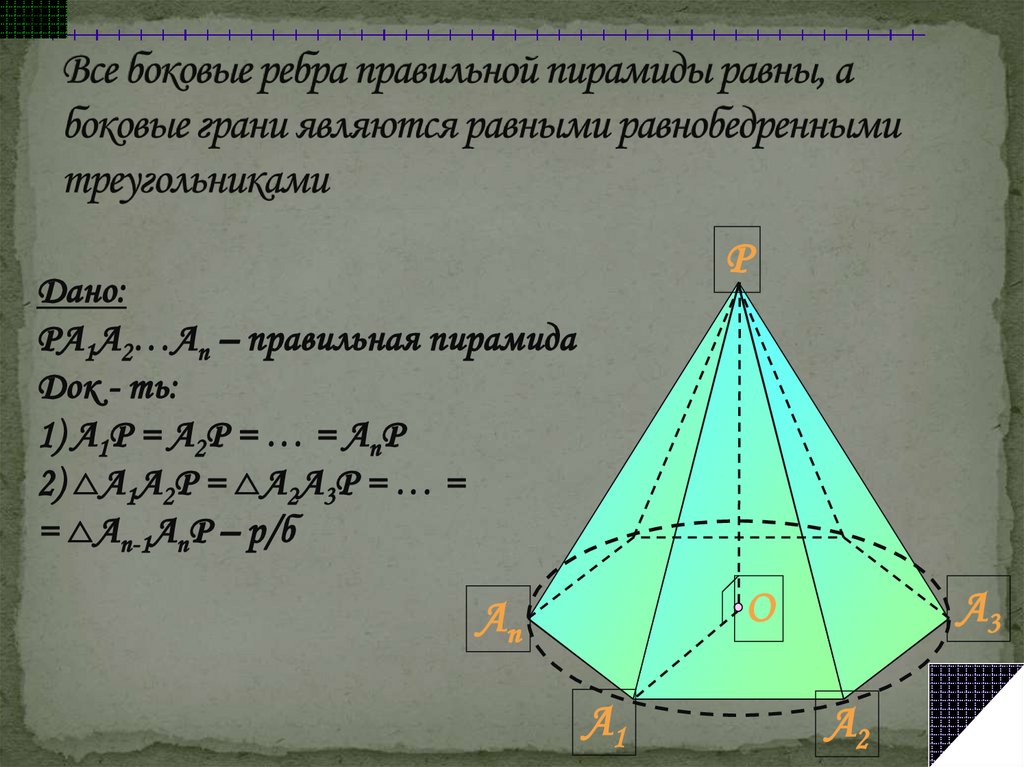
P
Все боковые ребра
правильной пирамиды
равны, а боковые грани
являются равными
равнобедренными
треугольниками
C
B
O
A
D

9.

Р
Дано:
PA1A2…An – правильная пирамида
Док - ть:
1) А1Р = А2Р = … = АnР
2) А1А2Р = А2А3Р = … =
= Аn-1АnР – р/б
О
Аn
А1
А3
А2

10.

1) Рассмотрим ОРА1 – п/у
РО – высота h, OA1 – радиус описанной окружности R
По теореме Пифагора:
Р
A1P= h2 + R2
A2P= h2 + R2 – любое боковое ребро
РА1 = РА2 =…= РАn
h
2) т. к. РА1 = РА2 =…= РАn,
поэтому
Боковые грани – р/б
Аn
О
Основания этих равны:
А1 А2 = А2 А3 = … = А 1 Аn
А1
А2
т. к. А1А2…Аn - правильный
А1А2Р = … = Аn-1АnР – р/б
многоугольник

11.

Высота боковой грани правильной пирамиды,
проведенная из её вершины называется
апофемой.
P
P
N
K
M
M
O
N
O
L
K

12.

Апофемы
Все апофемы
правильной пирамиды
равны друг другу

13.

Площадь боковой поверхности правильной
пирамиды равна половине произведения
периметра основания на апофему
Sбок = ½lP
Док – во:
Sбок = (½al+ ½al+ ½al)=
= ½l(a + a + a)= ½lP
l
a

14.

М
D
О
А
К
В
- боковые ребра равны
- боковые грани
равные
равнобедренные
треугольники
- углы наклона боковых
ребер к плоскости
С основания равны
- углы наклона боковых
N
граней к плоскости
основания равны
- апофемы равны

15.

Sбок. = (Pосн. * l) : 2
где
Pосн. – периметр основания,
l –апофема правильной пирамиды.

16.

В правильной четырехугольной
пирамиде SABCD точка O - центр
основания, S -вершина, SO = 4,
SC = 5.
Найдите длину отрезка AC.
.

17.

В правильной треугольной
пирамиде SABC R - середина
ребра BC, S - вершина. Известно,
что AB = 1, а SR = 2.
Найдите площадь боковой
поверхности.