Пирамида

1. Урок геометрии по теме:

2. Историчекая справка

• Термин «пирамида» заимствован из греческого
«пирамис» или «пирамидос». Греки в свою очередь
позаимствовали это слово из египетского языка. В
папирусе Ахмеса встречается слово «пирамис» в
смысле ребра правильной пирамиды. Другие
считают, что термин берет свое начало от формы
хлебцев в Древней Греции («пирос» - рожь). В связи
с тем, что форма пламени напоминает образ
пирамиды, некоторые ученые считали, что термин
происходит от греческого слова «пир» - огонь. В
Древнем Египте гробницы фараонов имели форму
пирамид

3. Гробницы фараонов (Египет)

4. Пирамиды в природе Гора Кайлас (Тибет)

5. Пирамиды в растениях

6. Пирамиды в архитектуре Стеклянная пирамида Лувра (Париж)

Спасская башня Кремля
(Москва)

7. Определение

Пирамида – многогранник, составленный из
n - угольника А1А2…Аn и n треугольников
Вершина
Высота –
перпендикуляр,
проведенный
из вершины
пирамиды к
плоскости
основания
P
Боковые грани
Основание
H
Боковые ребра
Аn
α
А1
Название пирамиды определяет n-угольник
А2

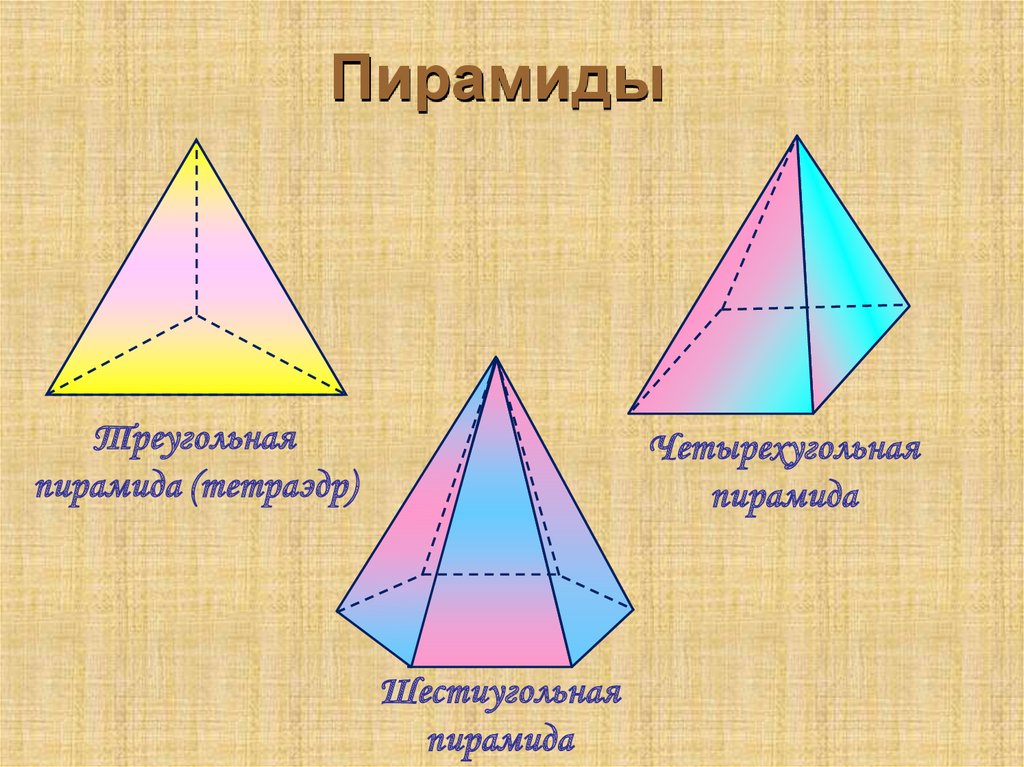
8. Пирамиды

Треугольная
пирамида (тетраэдр)
Четырехугольная
пирамида
Шестиугольная
пирамида

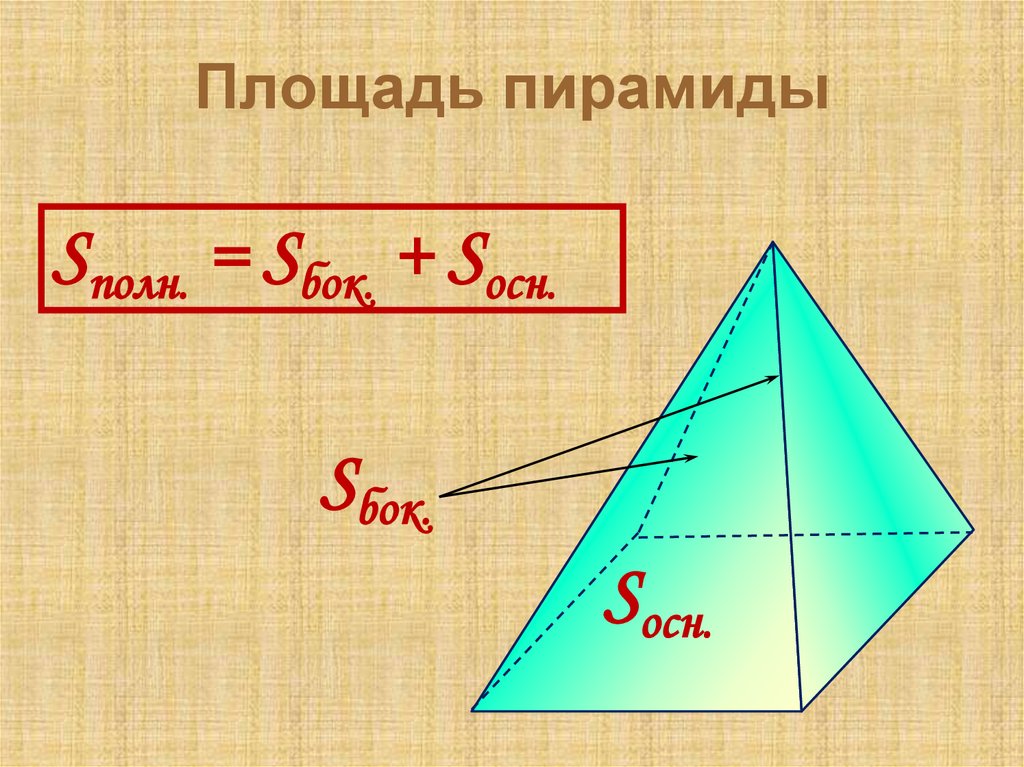
9. Площадь пирамиды

Sполн. = Sбок. + Sосн.
Sбок.
Sосн.

10. Площадь пирамиды

Sполн. = Sбок. + Sосн.
Sбок.
Sосн.

11. Правильная пирамида

Пирамида называется правильной, если ее основание –
правильный многоугольник, а отрезок, соединяющий вершину
пирамиды с центром основания, является ее высотой
P
h
O
Аn
А1
А3
А2

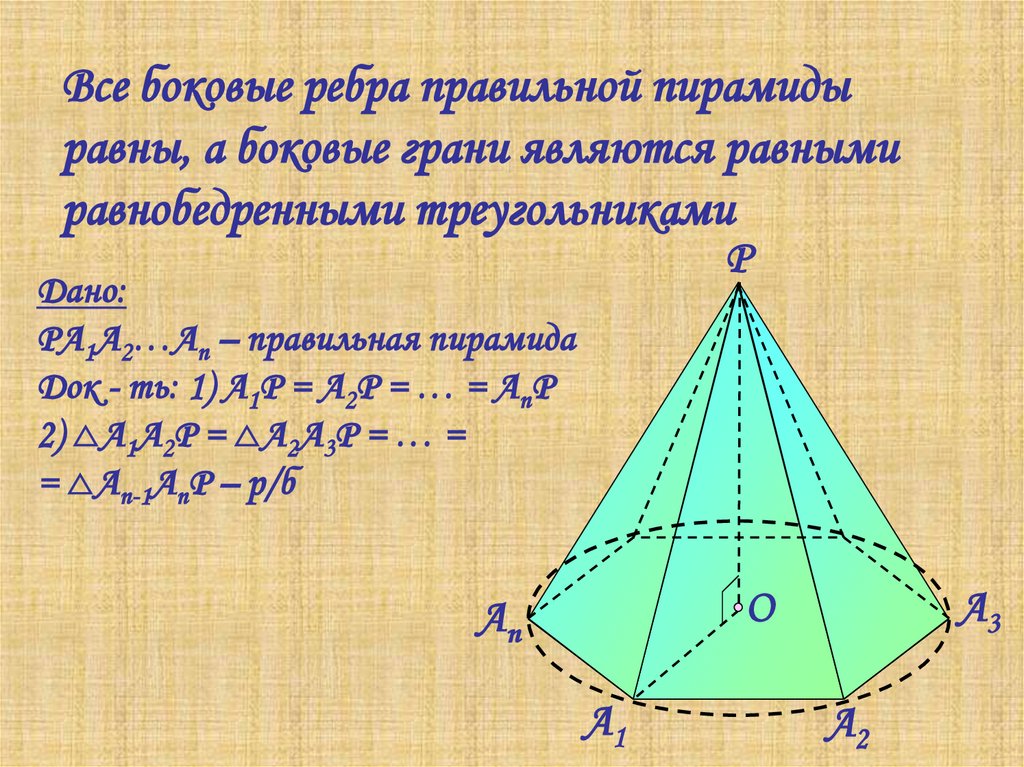
12. Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками

Р
Дано:
PA1A2…An – правильная пирамида
Док - ть: 1) А1Р = А2Р = … = АnР
2) А1А2Р = А2А3Р = … =
= Аn-1АnР – р/б
О
Аn
А1
А3
А2

13. Док – во:

1) Рассмотрим ОРА1 – п/у
РО – высота h, OA1 – радиус описанной окружности R
По теореме Пифагора:
Р
A1P= h2 + R2
A2P= h2 + R2 – любое боковое ребро
РА1 = РА2 =…= РАn
h
2) т. к. РА1 = РА2 =…= РАn,
поэтому
Боковые грани – р/б
Аn
О
Основания этих равны:
А1 А2 = А2 А3 = … = А 1 Аn
А1
А2
т. к. А1А2…Аn - правильный
А1А2Р = … = Аn-1АnР – р/б
многоугольник

14. Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины

Апофемы
Все апофемы
правильной пирамиды
равны друг другу

15. Теорема о площади боковой поверхности правильной пирамиды

Площадь боковой поверхности правильной
пирамиды равна половине произведения
периметра основания на апофему
Sбок = ½dP
Док – во:
Sбок = (½ad + ½ad + ½ad) =
= ½d(a + a + a)= ½dP
d
a