Похожие презентации:
Задача аппроксимации. Виды интерполяции. Параболическая интерполяция. Единственность интерполяционного многочлена. (Лекция 3)
1. Лекция 3
1. Постановка задачи. Применениеинтерполяции
2. Виды интерполяции. Параболическая
интерполяция. Единственность
интерполяционного многочлена
3. Интерполяционный многочлен
Лагранжа. Схема Эйткена
2. Задача аппроксимации
Задачааппроксимации
состоит
в
приближенной замене функции f(x), заданной
таблично, на некоторую функцию ϕ(х) так, чтобы
отклонение ϕ(х) от f(x) в некоторой области
удовлетворяло заданному условию. Функция ϕ(х)
называется аппроксимирующей функцией.
В качестве аппроксимирующей функции часто
используют алгебраический многочлен вида:
ϕn(x) = a0 + a1x + a2x2 + … + anxn
В этом случае говорят о параболической
аппроксимации.
Интерполяция является важным частным
случаем аппроксимации.
3. Постановка задачи интерполяции
Пусть функция y = f(x) задана таблицей значений вn+1 точке:
x
x0
x1
x2
…
xn
y
y0
y1
y2
…
yn
так, что y0 = f(x0), y1 = f(x1), y2 = f(x2), … yn = f(xn).
Требуется найти функцию F(x), приближающую функцию
f(x) (f(x) = F(x) + R(x), где R(x) – погрешность
интерполяции), совпадающую с функцией f(x) в точках xi
(i=0, 1, 2, …n). Функция f(x) называется
интерполируемой, F(x) – интерполирующей, точки xi
(i=0, 1, 2, …n) – узлами интерполяции.
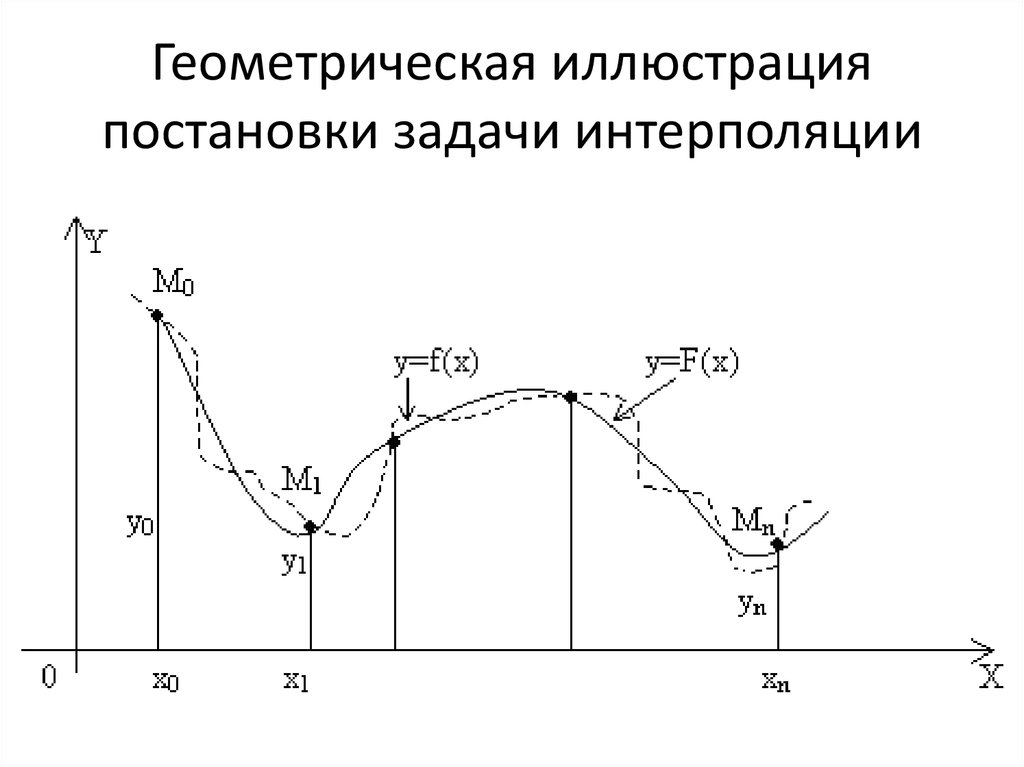
4. Геометрическая иллюстрация постановки задачи интерполяции
5. Применение интерполяции
1) интерполяция используется в тех случаях, когдаинтерполируемая функция известна лишь при
некоторых дискретных значениях аргумента xi, а
требуется получить ее приближенные значения в
других точках x≠ xi:
• если f(xi) – результаты эксперимента (измерений);
• если f(xi) – результаты сложных вычислений на
компьютере, например, результаты имитационного
моделирования;
• если f(xi) – табличные значения некоторой
элементарной или специальной функции, а
требуется получить таблицу с меньшим шагом или
значение функции при x≠ xi.
6. Применение интерполяции
2)интерполяция
используется
при
решении ряда других задач вычислительной
математики:
• приближенное
нахождение
корня
уравнения f(x) = 0 методом обратной
интерполяции;
• численное
дифференцирование
и
интегрирование функции f(x);
• приближенное определение экстремума
функции f(x).
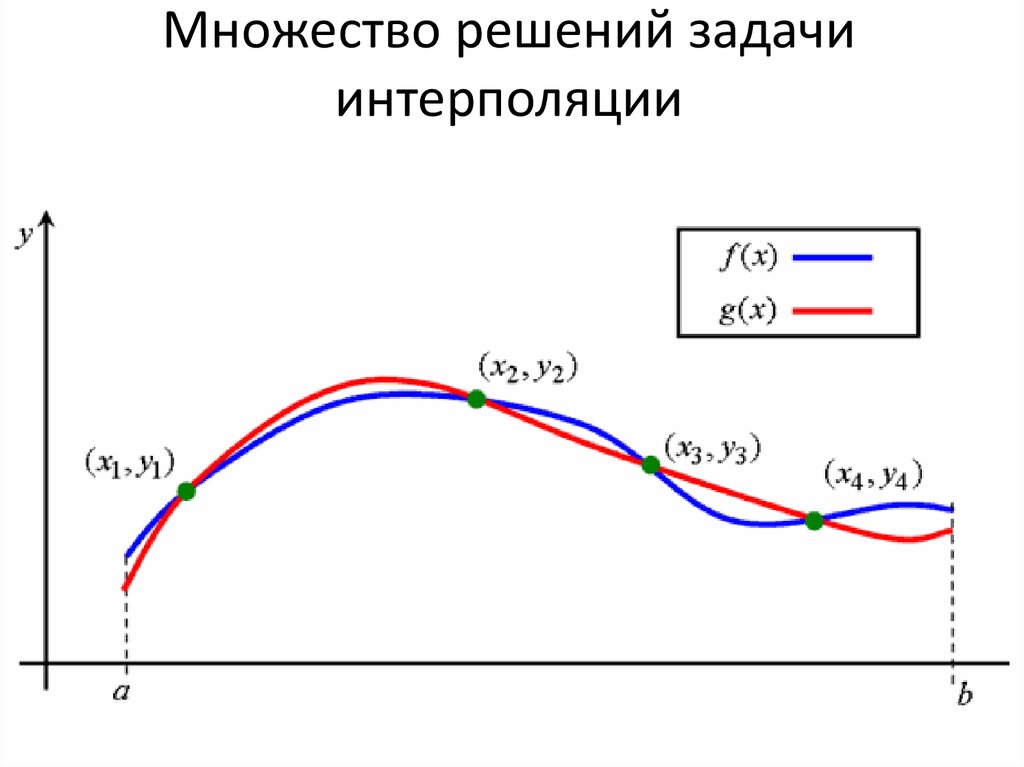
7. Множество решений задачи интерполяции
8. Виды интерполяции
В зависимости от класса интерполирующей функции различаютследующие виды интерполяции:
1) тригонометрическую интерполяцию
n
F(x) ( a i sinc i x b i cosci x)
i 0
2) экспоненциальную интерполяцию
n
F(x) a i e bi x
i 0
3) параболическую интерполяцию
n
F(x) Pn (x) a i x i a 0 a 1 x a 2 x 2 a n x n
i 0
9. Постановка задачи параболической интерполяции
Функция y = f(x) задана таблицей значений вn+1 точке:
y0 = f(x0), y1 = f(x1), y2 = f(x2), … yn = f(xn).
Требуется найти многочлен Pn(x) степени n,
значения которого
Pn(xi) = f(xi), i=0, 1, 2, … n.
10. Единственность интерполяционного многочлена
Найти многочлен Pn(x) = a0 + a1x + a2x2 +…+anxn – это значит, отыскатьего коэффициенты ai, i = 0, 1, 2, … n. Из условия интерполяции Pn(xi) = f(xi),
i=0, 1, 2, … n можно записать следующую систему линейных уравнений с
n+1 неизвестными коэффициентами ai:
a0 + a1x0 + a2x02 + … + anx0n = f(x0)
a0 + a1x1 + a2x12 + … + anx1n = f(x1)
………………………………………
a0 + a1xn + a2xn2 + … + anxnn = f(xn)
Определитель этой системы (определитель Вандермонда)
1 x 0 x 02 x n0
2
n
1
x
x
x
1
1
1
d
(x i x j ) 0
0 j i n
1 x n x n2 x nn
Следовательно, система линейных уравнений имеет решение, и притом –
единственное, что и доказывает единственность интерполяционного
многочлена.
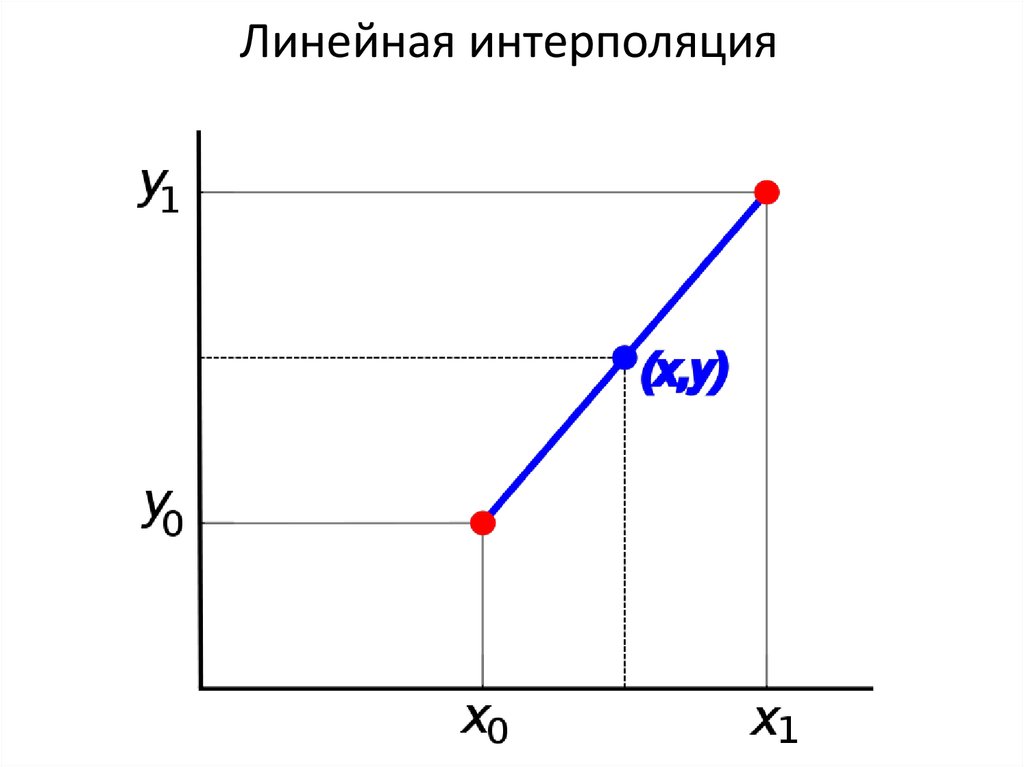
11. Линейная интерполяция
12. Пример построения интерполяционного многочлена непосредственным решением СЛУ
Таким образом, отыскать интерполяционный многочлен можнонепосредственным решением системы линейных уравнений. Пусть,
например, интерполируемая функция f(x) задана в трех точках:
x 0 1 2
y 1 1 3
Требуется найти многочлен 2–й степени P2(x) = a0 + a1x + a2x2.
СЛУ относительно неизвестных коэффициентов многочлена будет
иметь следующий вид:
a0 + a1∙0 + a2∙02 = 1
a0 + a1∙1 + a2∙12 = 1
a0 + a1∙2 + a2∙22 = 3
а ее решение: a0 = 1, a1 = –1, a2 = 1. Искомый интерполяционный многочлен
P2(x) = 1 – x + x2
13. Интерполяционная формула Лагранжа
Будем искать Ln(x) в виде:Ln(x) = Q0(x)∙y0 + Q1(x)∙y1 + … + Q n(x)∙yn,
где Qi(x) – коэффициенты, зависящие только от узлов xi (i=0, 1, 2, …n) и
текущего значения х.
Для того чтобы выполнялись условия интерполяции, требуется, чтобы
в узлах интерполяции коэффициенты Qi(x) удовлетворяли условию:
0, если j i,
Q i (x j )
1, если j i
Это условие выполняется, если представить Qi(x) в виде:
(x x 0 )(x x1 ) (x x i 1 )(x x i 1 ) (x x n 1 )(x x n )
Q i (x)
(x i x 0 )(x i x1 ) (x i x i 1 )(x i x i 1 ) (x i x n 1 )(x i x n )
14. Интерполяционная формула Лагранжа
Qi(x) – многочлен n–й степени, так как в числителе произведение nлинейных сомножителей. При x = xi числитель и знаменатель выражения
равны, и Qi(xi) = 1. При x = xj (j ≠ i) один из сомножителей числителя
обращается в 0, и таким образом Qi(xj) = 0 при j ≠ i.
Тогда многочлен Qi(x)∙yi будет принимать значение yi при x = xi и 0 при
x = xj (j ≠ i). Многочлен степени n
(x x 0 )(x x1 ) (x x i 1 )(x x i 1 ) (x xn 1 )(x xn )
Ln (x)
yi
i 0 (x i x 0 )(x i x1 ) (x i x i 1 )(x i x i 1 ) (x i x n 1 )(x i x n )
n
будет в узлах xi принимать значения yi, следовательно, Ln(x) –
интерполяционный многочлен.
15. Интерполяционная формула Лагранжа
Полученная формула называется интерполяционныммногочленом Лагранжа. Несмотря на некоторую
громоздкость, одним из преимуществ формулы
Лагранжа
является
возможность
ее
записи
непосредственно по заданной таблице значений
функции. При этом следует учитывать следующие
правила:
• формула содержит столько слагаемых, сколько узлов в
таблице;
• каждое слагаемое – это произведение дробного
коэффициента на соответствующее значение yi;
• числитель коэффициента при yi содержит
произведение разностей х со всеми узлами кроме xi,
а знаменатель полностью повторяет числитель при
подстановке х = xi.
16. Формулы Лагранжа для линейной и квадратичной интерполяции
Пусть n = 1 (два узла). Тогдаx x 0
x x1
L1 (x)
y0
y1
x 0 x1
x1 x 0
Для трех узлов (n = 2) получим:
(x x 0 )(x x 2 )
(x x 0 )(x x1 )
(x x1 )(x x 2 )
L 2 (x)
y0
y1
y2
(x 0 x1 )(x 0 x 2 )
(x1 x 0 )(x1 x 2 )
(x 2 x 0 )(x 2 x1 )
17. Пример использования формулы Лагранжа
Пусть интерполируемая функция f(x) задана той же таблицей,что и в предыдущем разделе. Требуется найти приближенное
значение функции в точке x = 0.5 путем квадратичной
интерполяции.
x
0
1
2
y
1
1
3
(x x 0 )(x x 2 )
(x x 0 )(x x1 )
(x x1 )(x x 2 )
L 2 (x)
y0
y1
y2
(x 0 x1 )(x 0 x 2 )
(x1 x 0 )(x1 x 2 )
(x 2 x 0 )(x 2 x1 )
(0.5 1)(0.5 2)
(0.5 0)(0.5 2)
(0.5 0)(0.5 1)
1
1
3
(0 1)(0 2)
(1 0)(1 2)
(2 0)(2 1)
0.75
0.75
0.25
1
1
3 0.75
2
1
2
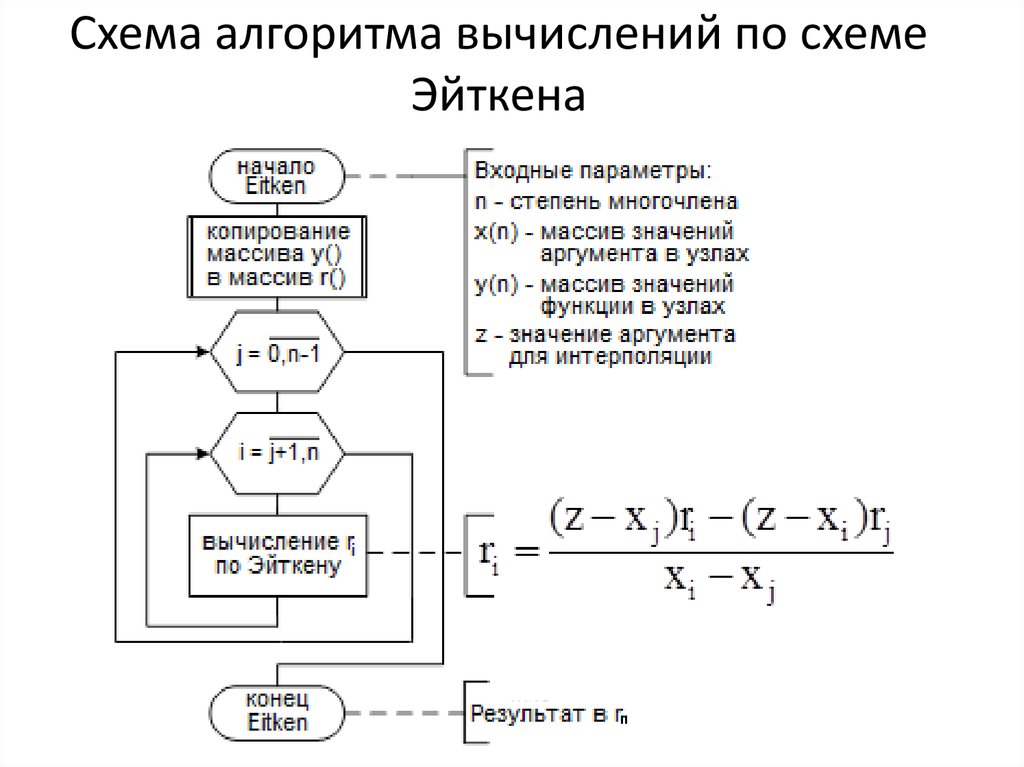
18. Интерполяционная схема Эйткена
y01
L1 (x) P0,1 (x)
x1 x 0 y 1
x0 x
x1 x
P0,1 (x) x 0 x
1
L 2 (x) P0,1,2 (x)
, где
x 2 x 0 P1,2 (x) x 2 x
y 1 x1 x
1
P1,2 (x)
x 2 x1 y 2 x 2 x
………………………………………………………………………………………………………
P0,1, ...n 1 (x) x 0 x
1
L n (x) P0,1, ...n (x)
x n x 0 P1, 2, ... n (x) x n x















 Математика
Математика








