Похожие презентации:
Параллелепипед. Определение. Виды. Свойства
1.
ПАРАЛЛЕЛЕПИПЕДОпределение. Виды. Свойства.
2.
ПАРАЛЛЕЛЕПИПЕДПараллелепипед – это призма, основание которой
параллелограмм. Другими словами,
параллелепипед – это многогранник с шестью
гранями, каждая грань которого параллелограмм.
Основания параллелепипеда расположены в
параллельных плоскостях.
Основанием параллелепипеда также может
быть параллелограмм, прямоугольник, квадрат.
3.
ПАРАЛЛЕЛЕПИПЕДСвойства параллелепипеда:
1. Противолежащие грани параллелепипеда равны и параллельны друг
другу.
2. Все 4 диагонали параллелепипеда пересекаются в одной точке и
делятся этой точкой пополам.
3. Параллелепипед симметричен
относительно середины его диагонали.
4. Квадрат длины диагонали
прямоугольного параллелепипеда равен
сумме квадратов трёх его измерений.
4.
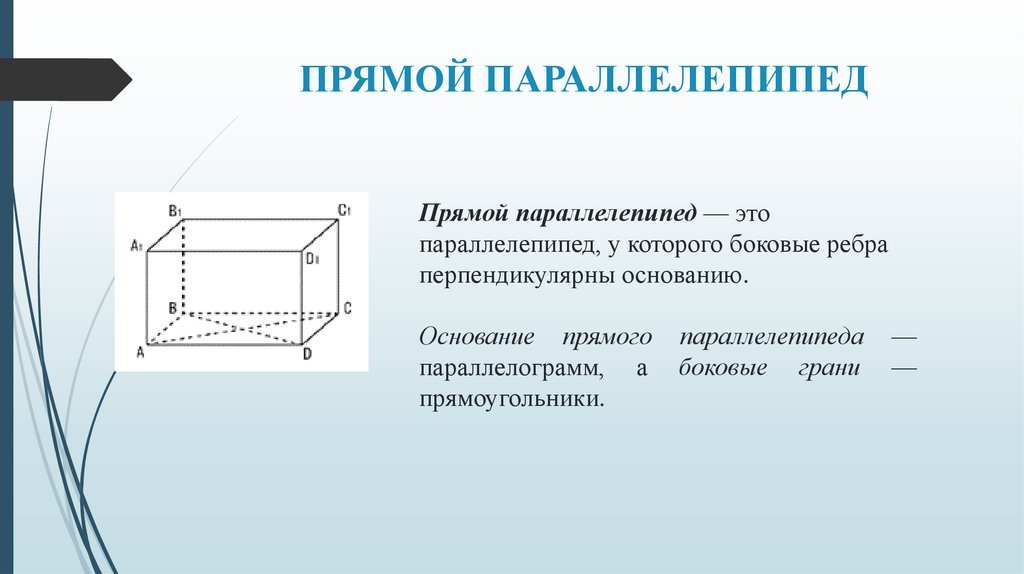
ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕДПрямой параллелепипед — это
параллелепипед, у которого боковые ребра
перпендикулярны основанию.
Основание прямого
параллелограмм, а
прямоугольники.
параллелепипеда
боковые грани
—
—
5.
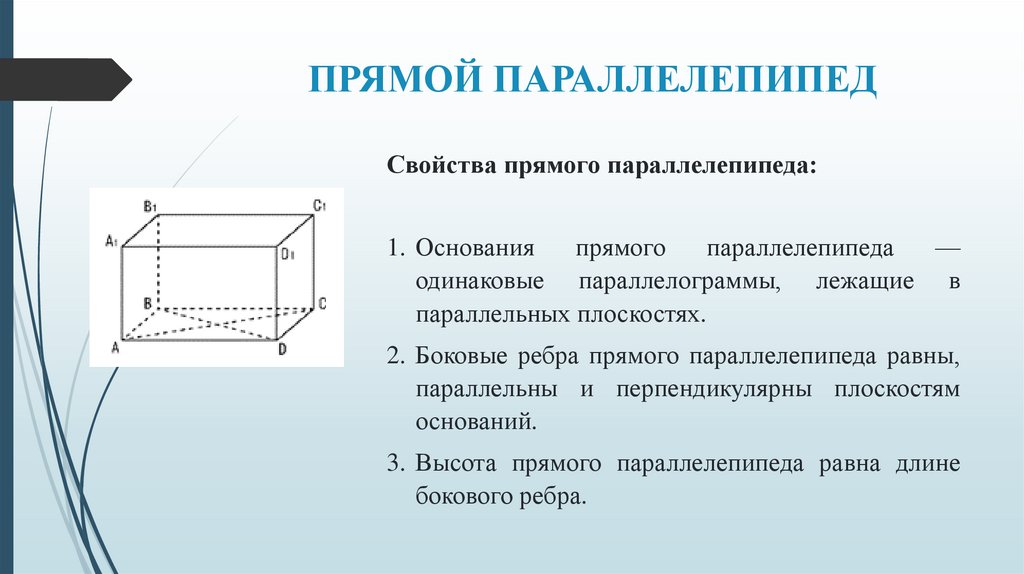
ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕДСвойства прямого параллелепипеда:
1. Основания
прямого
параллелепипеда
—
одинаковые параллелограммы, лежащие в
параллельных плоскостях.
2. Боковые ребра прямого параллелепипеда равны,
параллельны и перпендикулярны плоскостям
оснований.
3. Высота прямого параллелепипеда равна длине
бокового ребра.
6.
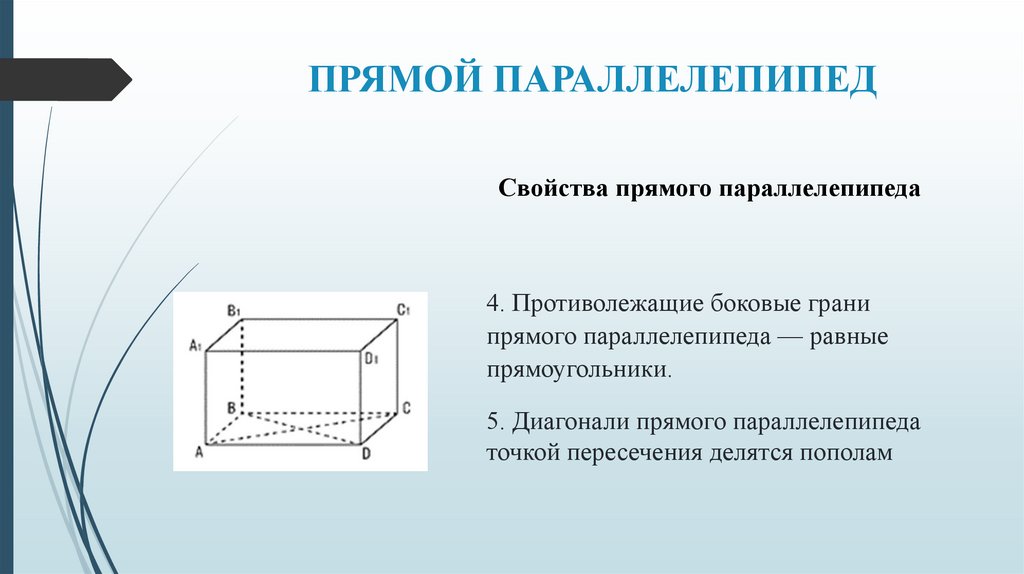
ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕДСвойства прямого параллелепипеда
4. Противолежащие боковые грани
прямого параллелепипеда — равные
прямоугольники.
5. Диагонали прямого параллелепипеда
точкой пересечения делятся пополам
7.
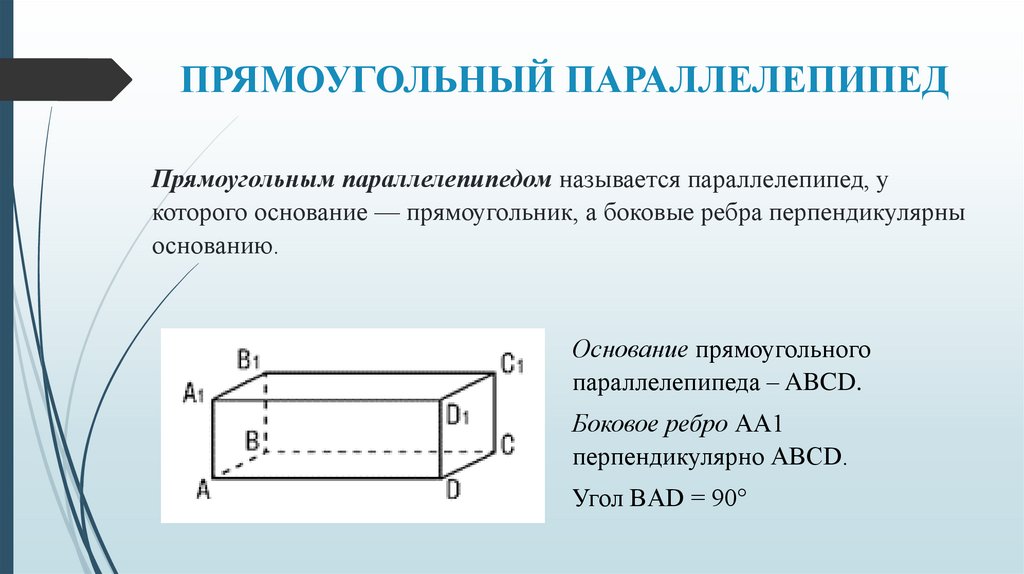
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕДПрямоугольным параллелепипедом называется параллелепипед, у
которого основание — прямоугольник, а боковые ребра перпендикулярны
основанию.
Основание прямоугольного
параллелепипеда – ABCD.
Боковое ребро АА1
перпендикулярно АВСD.
Угол BAD = 90°
8.
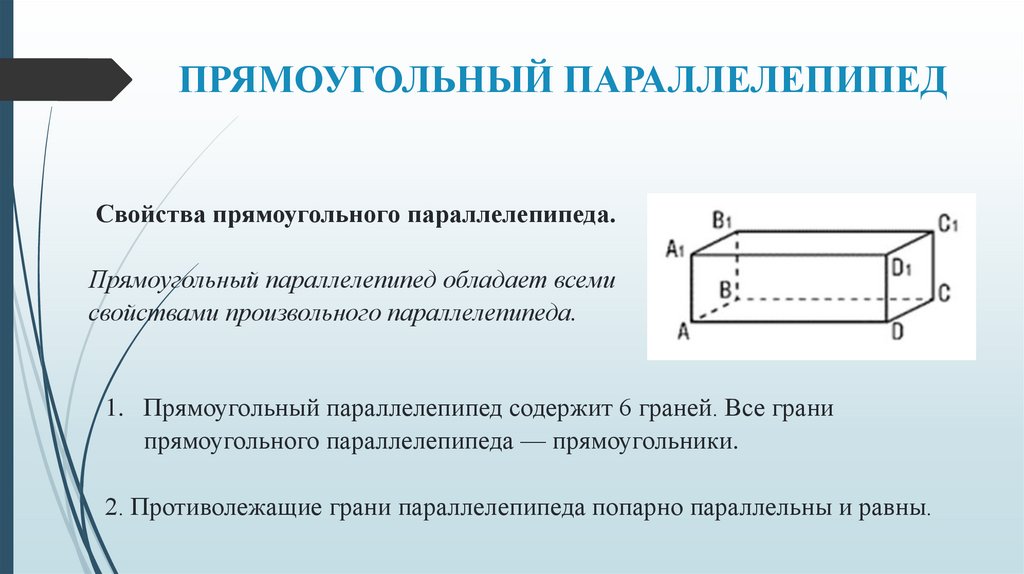
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕДСвойства прямоугольного параллелепипеда.
Прямоугольный параллелепипед обладает всеми
свойствами произвольного параллелепипеда.
1. Прямоугольный параллелепипед содержит 6 граней. Все грани
прямоугольного параллелепипеда — прямоугольники.
2. Противолежащие грани параллелепипеда попарно параллельны и равны.
9.
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕДСвойства прямоугольного параллелепипеда
3. Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
4. Диагонали прямоугольного параллелепипеда равны.
5. В прямоугольном параллелепипеде четыре
диагонали, которые пересекаются в одной
точке и делятся этой точкой пополам.
6. Любая грань прямоугольного параллелепипеда
может быть принята за основание.
10.
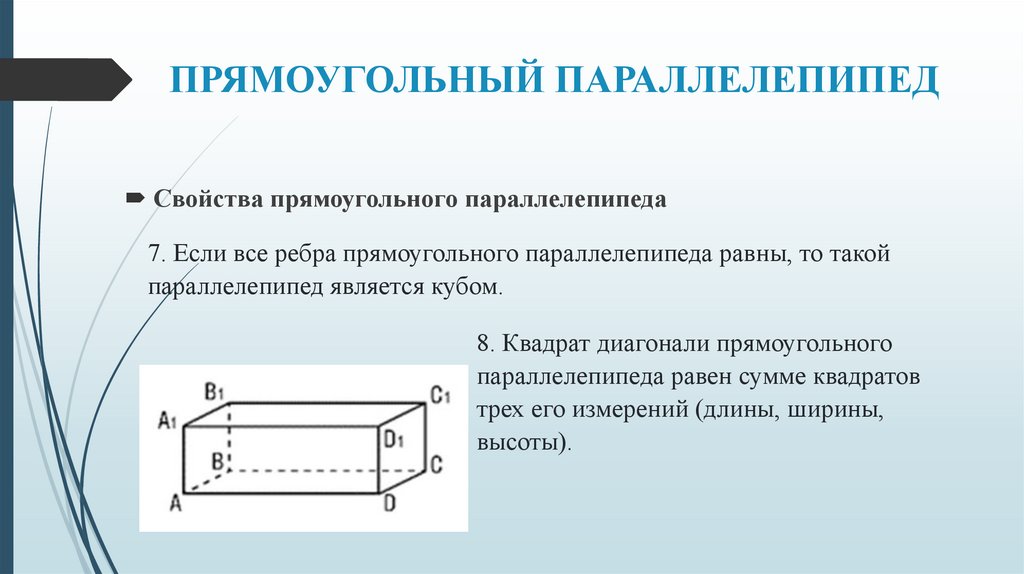
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕДСвойства прямоугольного параллелепипеда
7. Если все ребра прямоугольного параллелепипеда равны, то такой
параллелепипед является кубом.
8. Квадрат диагонали прямоугольного
параллелепипеда равен сумме квадратов
трех его измерений (длины, ширины,
высоты).
11.
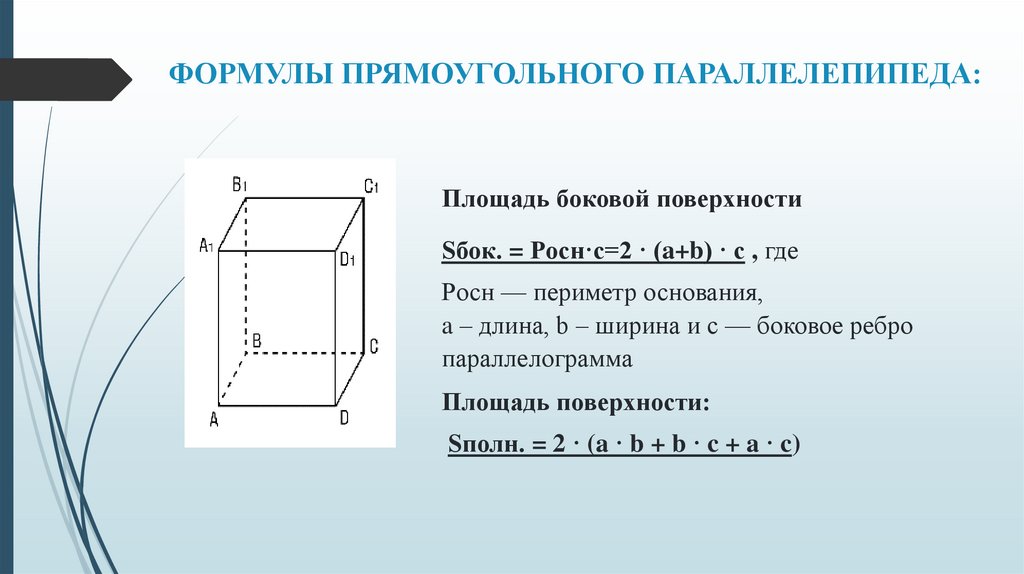
ФОРМУЛЫ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА:Площадь боковой поверхности
Sбок. = Pосн·c=2 · (a+b) · c , где
Pосн — периметр основания,
a – длина, b – ширина и с — боковое ребро
параллелограмма
Площадь поверхности:
Sполн. = 2 · (a · b + b · c + a · c)
12.
ПРОСТРАНСТВЕННАЯ ТЕОРЕМА ПИФАГОРАКвадрат диагонали прямоугольного параллелепипеда равен сумме
квадратов трех его измерений.
В данном случае, три измерения — это
длина, ширина, высота.
Длина, ширина и высота — это длины трех
ребер, исходящих из одной вершины
прямоугольного параллелепипеда. Дан
прямоугольный параллелепипед
ABCDA1B1C1D1.
Доказать теорему.
13.
ПРОСТРАНСТВЕННАЯ ТЕОРЕМА ПИФАГОРАДоказательство теоремы:
Необходимо найти диагональ
прямоугольного параллелепипеда.
Диагональ — это отрезок, соединяющий
противоположные вершины
параллелограмма.
14.
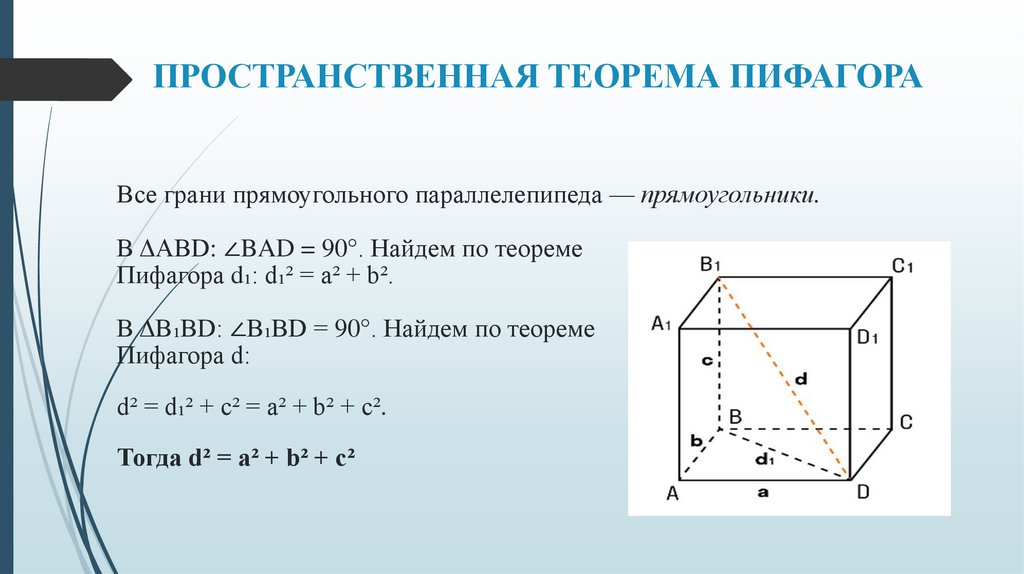
ПРОСТРАНСТВЕННАЯ ТЕОРЕМА ПИФАГОРАВсе грани прямоугольного параллелепипеда — прямоугольники.
В ΔABD: ∠BAD = 90°. Найдем по теореме
Пифагора d₁: d₁² = a² + b².
В ΔB₁BD: ∠B₁BD = 90°. Найдем по теореме
Пифагора d:
d² = d₁² + c² = a² + b² + c².
Тогда d² = a² + b² + c²
15.
КУБОпределение , свойства и формулы.
16.
КУБ.Кубом называется прямоугольный
параллелепипед, все три измерения которого
равны.
Каждая грань куба — это квадрат.
17.
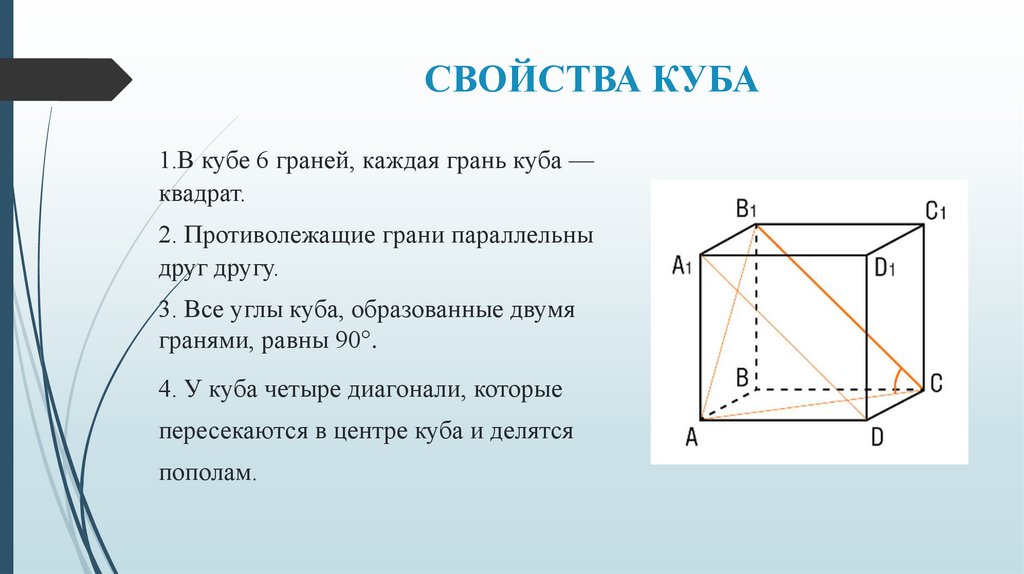
СВОЙСТВА КУБА1.В кубе 6 граней, каждая грань куба —
квадрат.
2. Противолежащие грани параллельны
друг другу.
3. Все углы куба, образованные двумя
гранями, равны 90°.
4. У куба четыре диагонали, которые
пересекаются в центре куба и делятся
пополам.
18.
СВОЙСТВА КУБА5. Диагонали куба равны.
6. Диагональ куба в √3 раз больше его
ребра: d = √3 a
7. Диагональ грани куба в √2 раза
больше длины ребра: d гр. = √2 a
19.
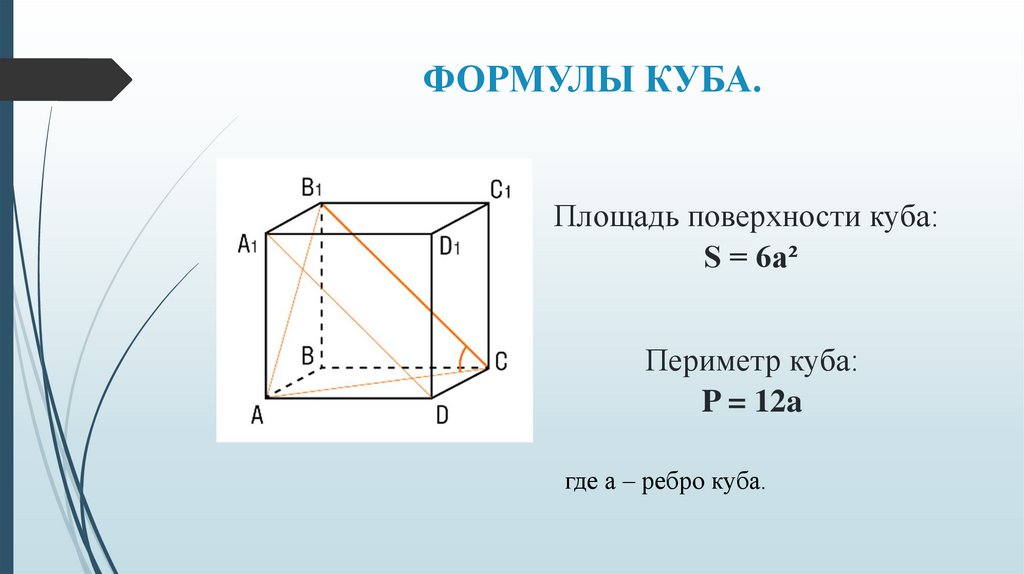
ФОРМУЛЫ КУБА.Площадь поверхности куба:
S = 6a²
Периметр куба:
P = 12a
где а – ребро куба.
20.
РЕШЕНИЕ ЗАДАЧЗАДАЧА 1.
Дан прямоугольный параллелепипед. Нужно найти сумму длин
всех ребер параллелепипеда и площадь его поверхности, если
а = 10 см, b = 5 см, с = 8 см.
21.
РЕШЕНИЕ ЗАДАЧЗАДАЧА 2.
Дан прямоугольный
параллелепипед АВСDA1B1C1D1.
D1B = √26 см,
BB1 = 3 см,
A1D1 = 4 см.
Найти длину ребра A1B1
22.
РЕШЕНИЕ ЗАДАЧЗАДАЧА 3.
Дан прямоугольный
параллелепипед АВСDA1B1C1D1.
AB = 4 см,
AD = 6 см,
AA1= 5 см.
Нужно найти отрезок BD1.
23.
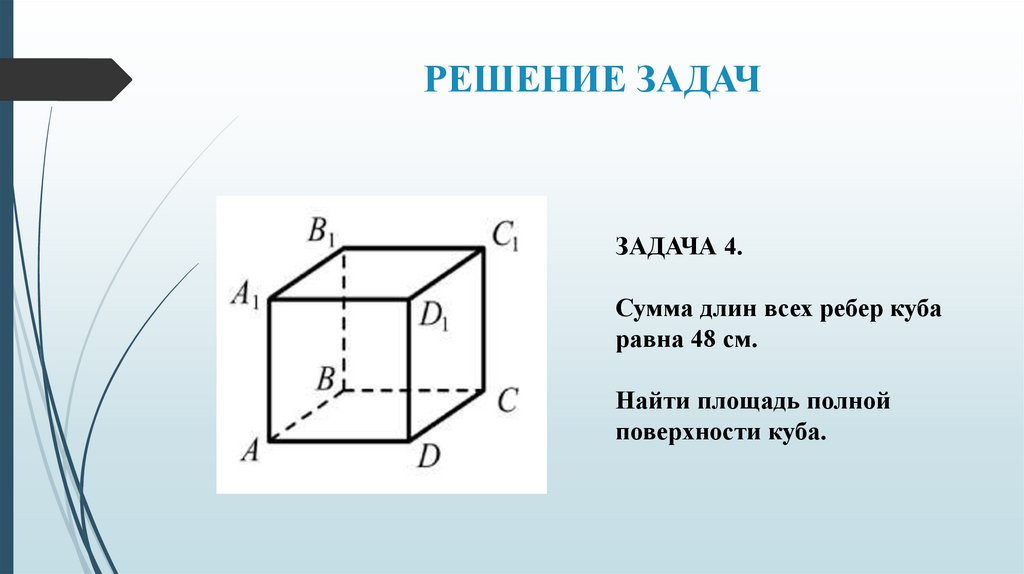
РЕШЕНИЕ ЗАДАЧЗАДАЧА 4.
Сумма длин всех ребер куба
равна 48 см.
Найти площадь полной
поверхности куба.












 Математика
Математика








