Параллелепипед, его виды и свойства

1.

Параллелепипед, его
виды и свойства
Шуст М.Н.

2. Основные вопросы:

1. Виды параллелепипеда (прямой,
прямоугольный). Элементы
параллелепипеда: вершины, грани,
ребра, смежные грани,
противоположные грани,
противолежащие вершины,
диагональ параллелепипеда, боковые
грани, основания, боковые ребра.
2. Свойства параллелепипеда.
2

3.

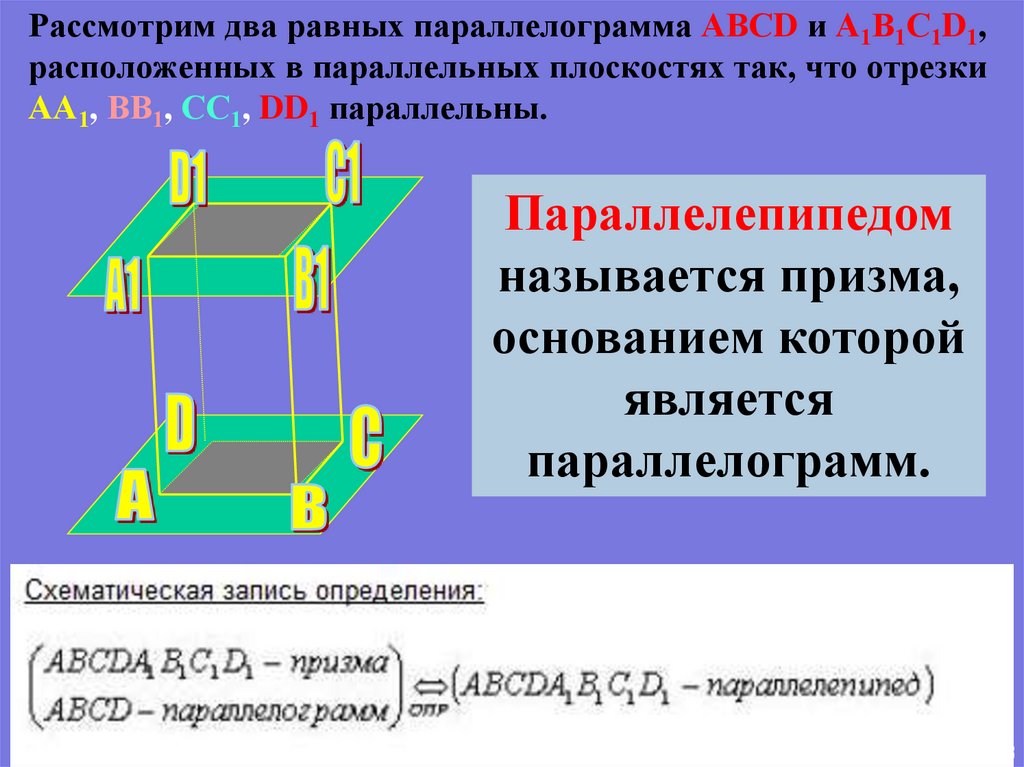
Рассмотрим два равных параллелограмма АВСD и А1В1С1D1,
расположенных в параллельных плоскостях так, что отрезки
АА1, ВВ1, СС1, DD1 параллельны.
Параллелепипедом
называется призма,
основанием которой
является
параллелограмм.
3

4. Элементы параллелепипеда.

1. Вершины параллелепипеда
D1
C1
B1
A1
D
A
C
B
4

5.

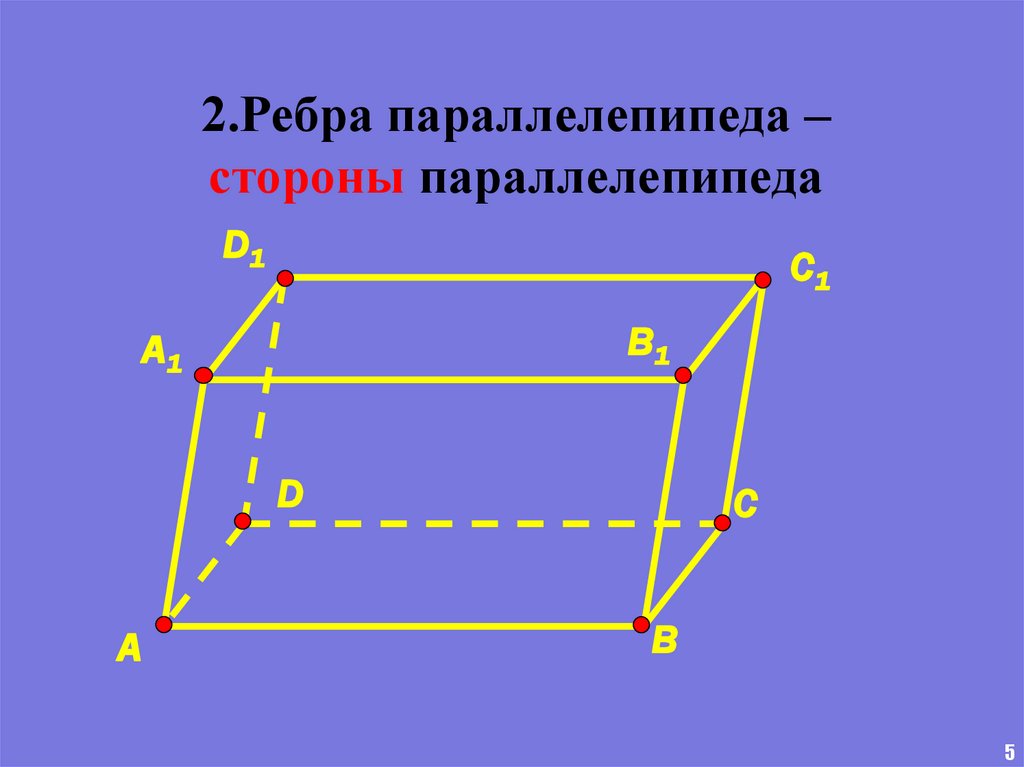
2.Ребра параллелепипеда –
стороны параллелепипеда
D1
C1
B1
A1
D
A
C
B
5

6.

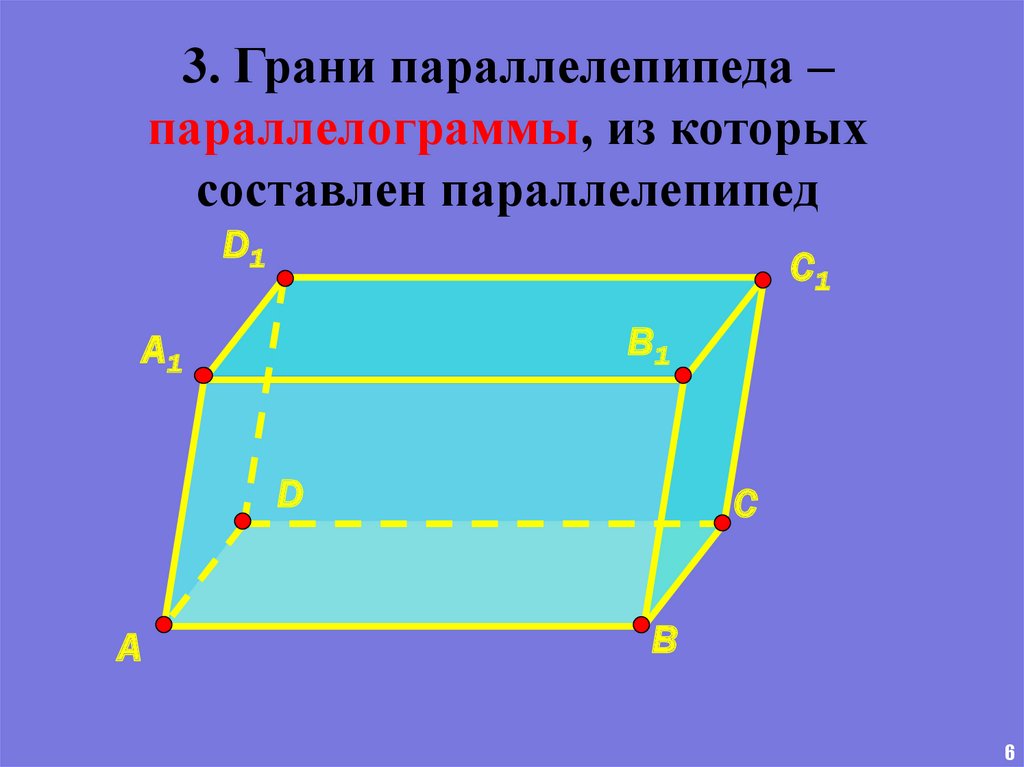
3. Грани параллелепипеда –
параллелограммы, из которых
составлен параллелепипед
D1
C1
B1
A1
D
A
C
B
6

7.

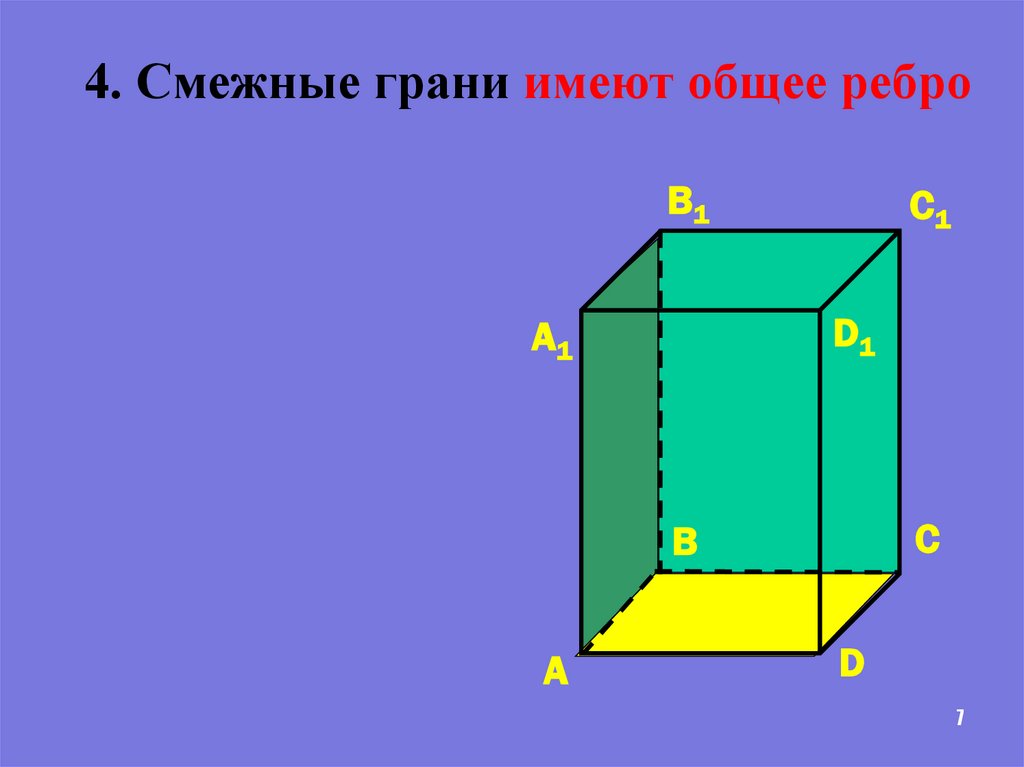
4. Смежные грани имеют общее ребро
B1
C1
D1
А1
C
B
А
D
7

8.

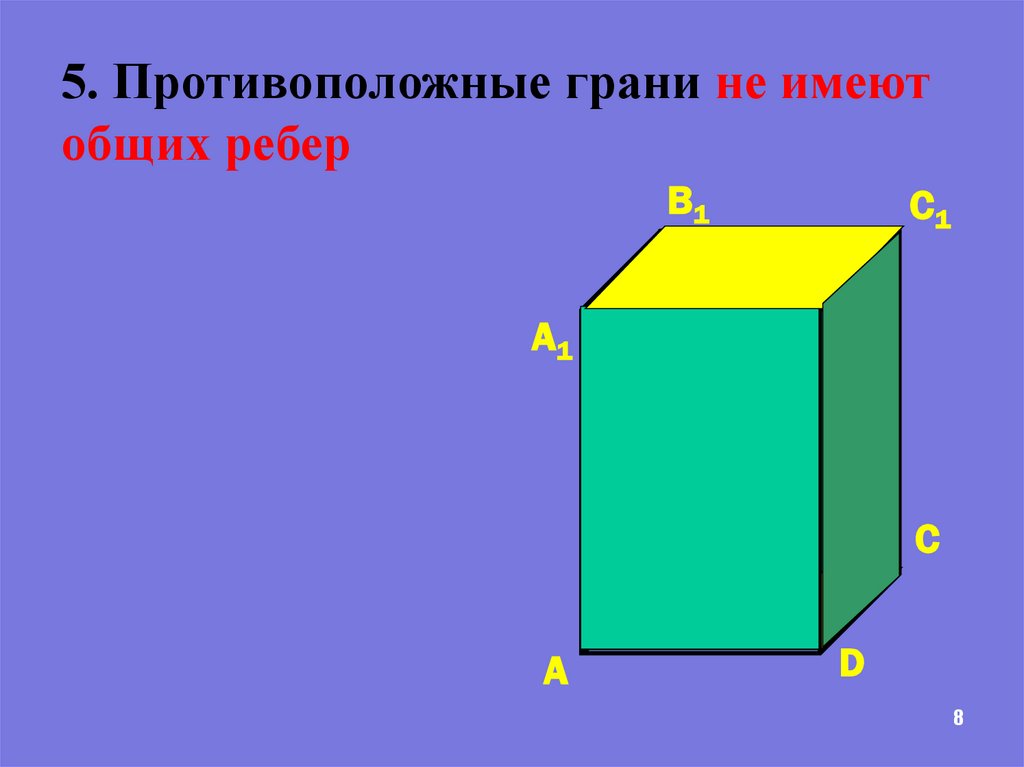
5. Противоположные грани не имеют
общих ребер
B1
C1
D1
А1
C
B
А
D
8

9.

6. Диагональ – отрезок, который
соединяет противоположные вершины
B1
C1
D1
А1
C
B
А
D

10.

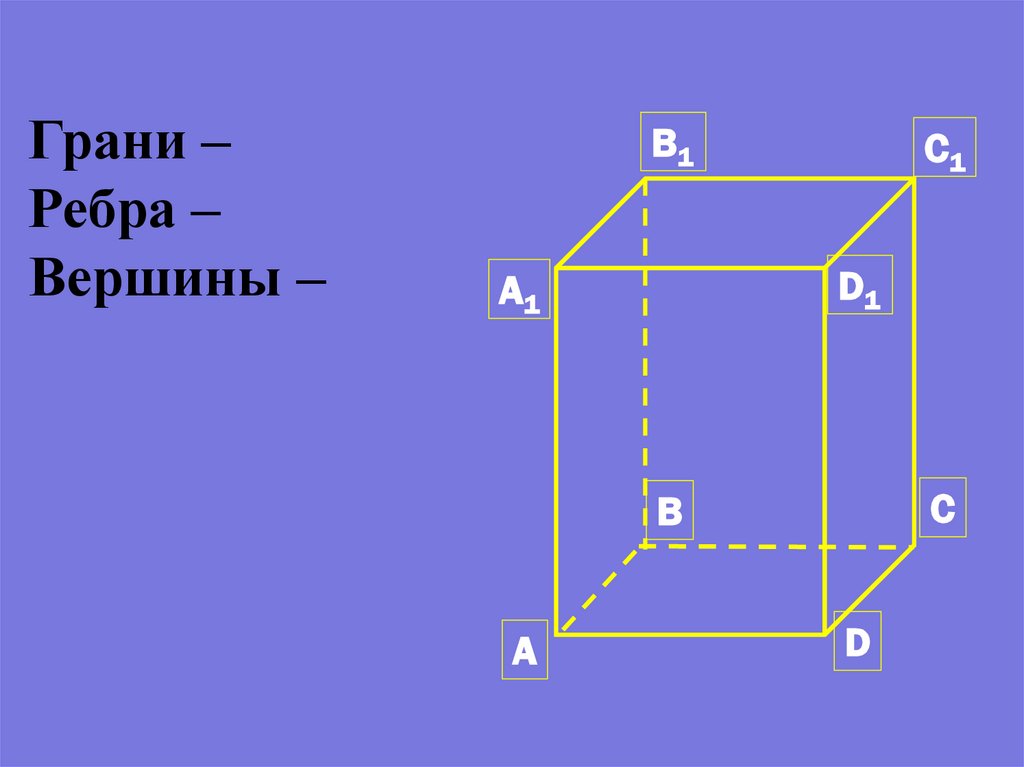
Грани –
Ребра –
Вершины –
B1
C1
D1
А1
C
B
А
D

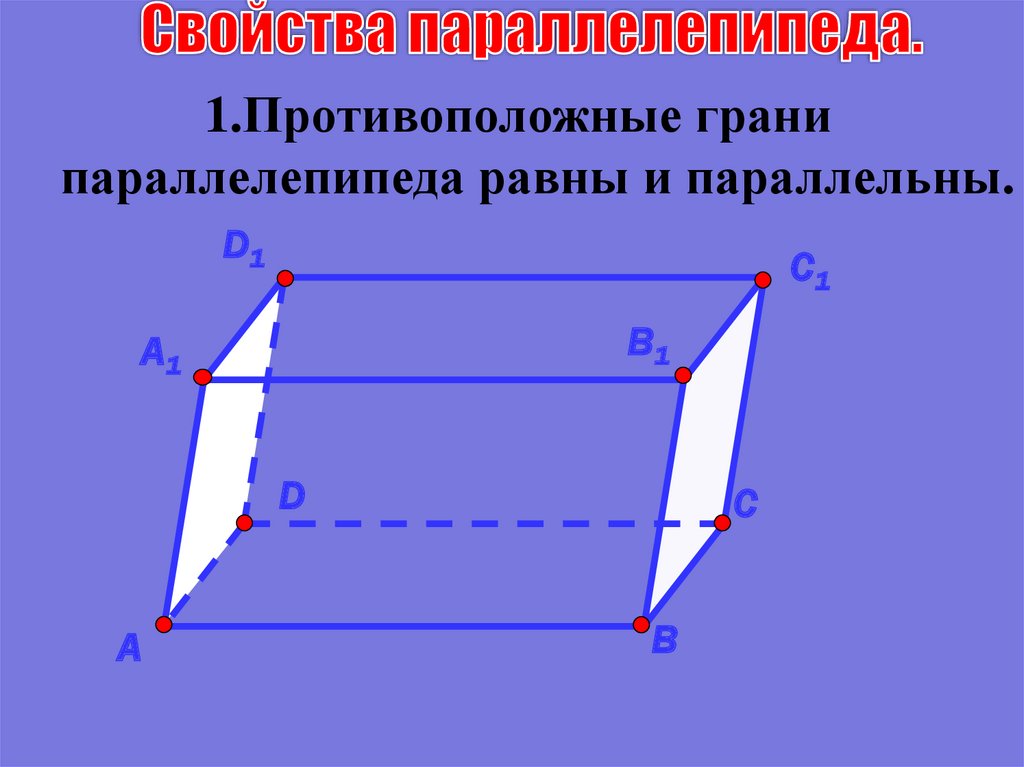
11. Свойства параллелепипеда.

1.Противоположные грани
параллелепипеда равны и параллельны.
D1
C1
B1
A1
D
A
C
B

12.

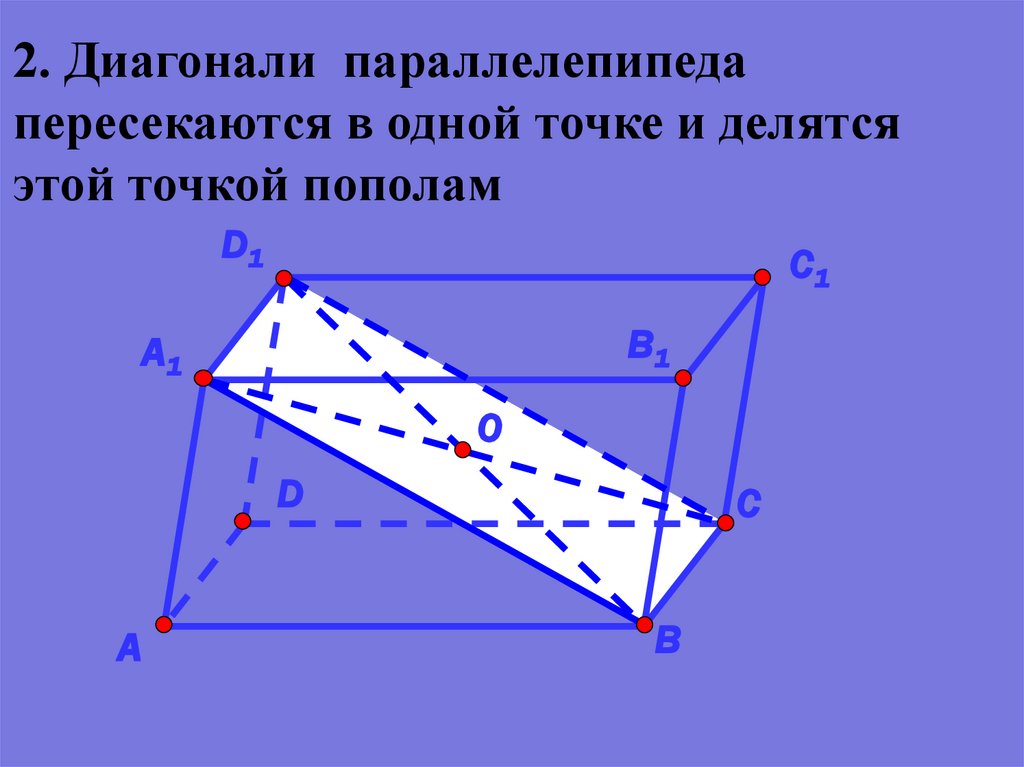
2. Диагонали параллелепипеда
пересекаются в одной точке и делятся
этой точкой пополам
D1
C1
B1
A1
O
D
A
C
B

13.

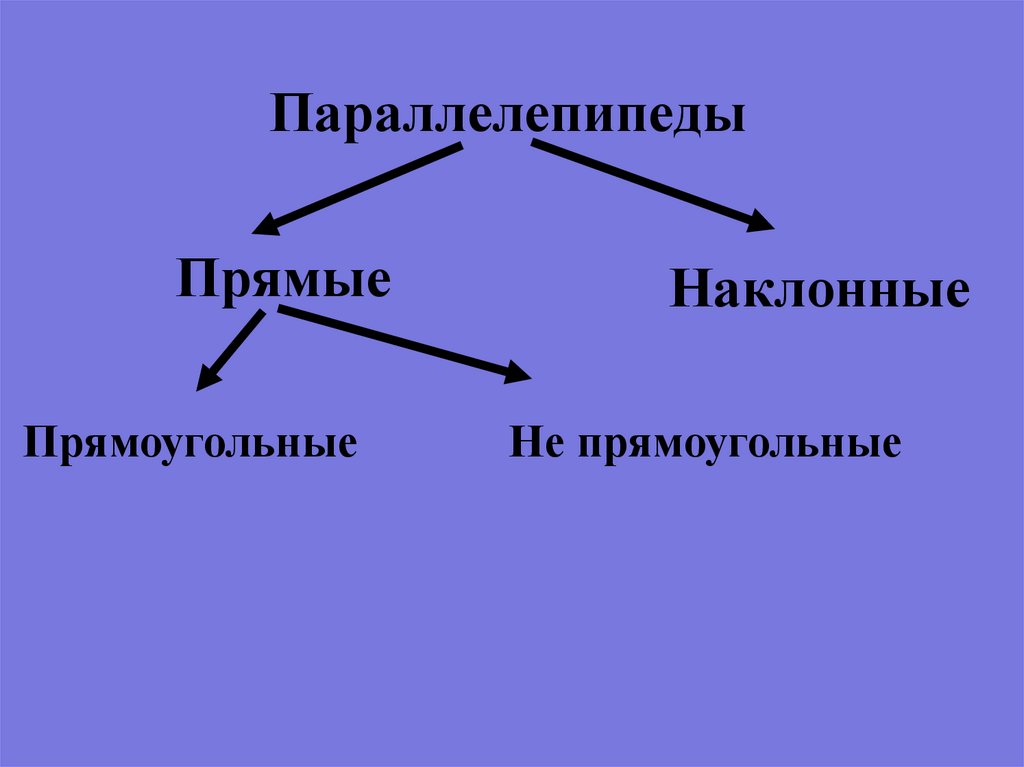
Параллелепипеды
Прямые
Прямоугольные
Наклонные
Не прямоугольные

14. Параллелепипед называется прямым, если его боковые рёбра перпендикулярны к основанию.

Параллелепипед называется прямым
если его боковые рёбра
перпендикулярны к основанию.
У прямого
параллелепипеда
боковые грани –
прямоугольники.
14

15. Параллелепипед называется прямоугольным, если его боковые рёбра перпендикулярны к основанию, а основанием является

прямоугольник
У прямоугольного
параллелепипеда все
грани - прямоугольники.
Диагонали
прямоугольного
параллелепипеда равны.
15

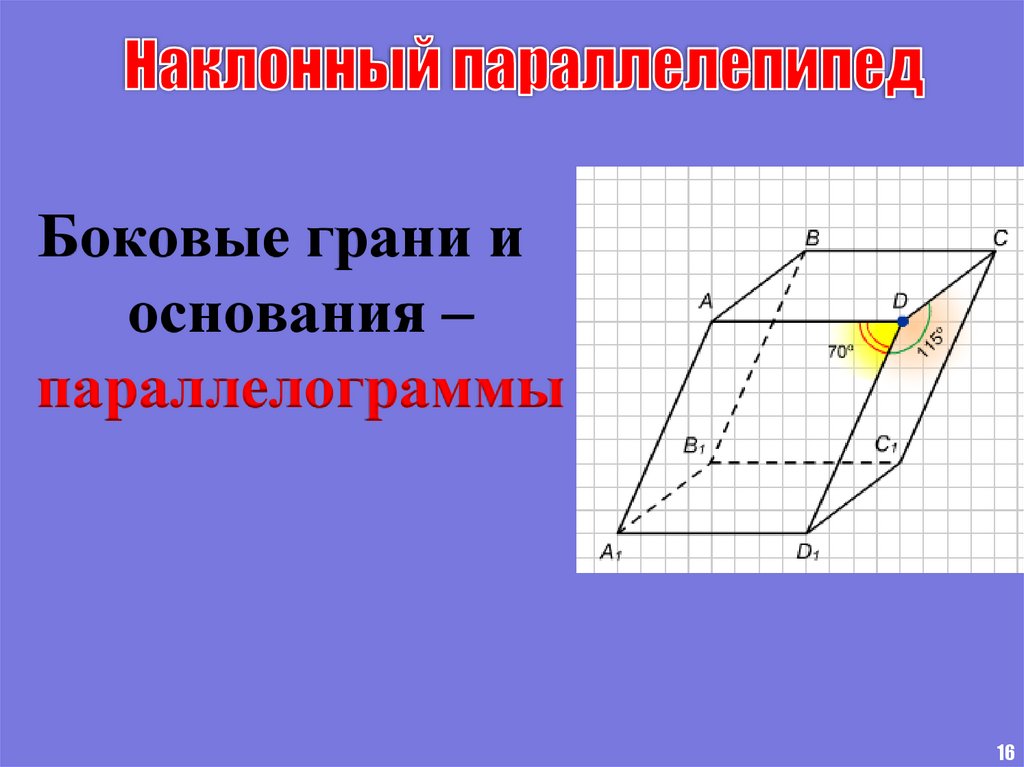
16. Наклонный параллелепипед

Боковые грани и
основания –
параллелограммы
16

17. Куб – прямоугольный параллелепипед, у которого все ребра равны между собой.

У куба все грани –
равные квадраты
Три ребра, выходящие из одной
вершины прямоугольного
параллелепипеда называются
его измерениями (длиной,
шириной, высотой).
17

18. Теорема:

a
d
c
b
2
d
=
2
a
+
2
b
2
+c .
18

19.

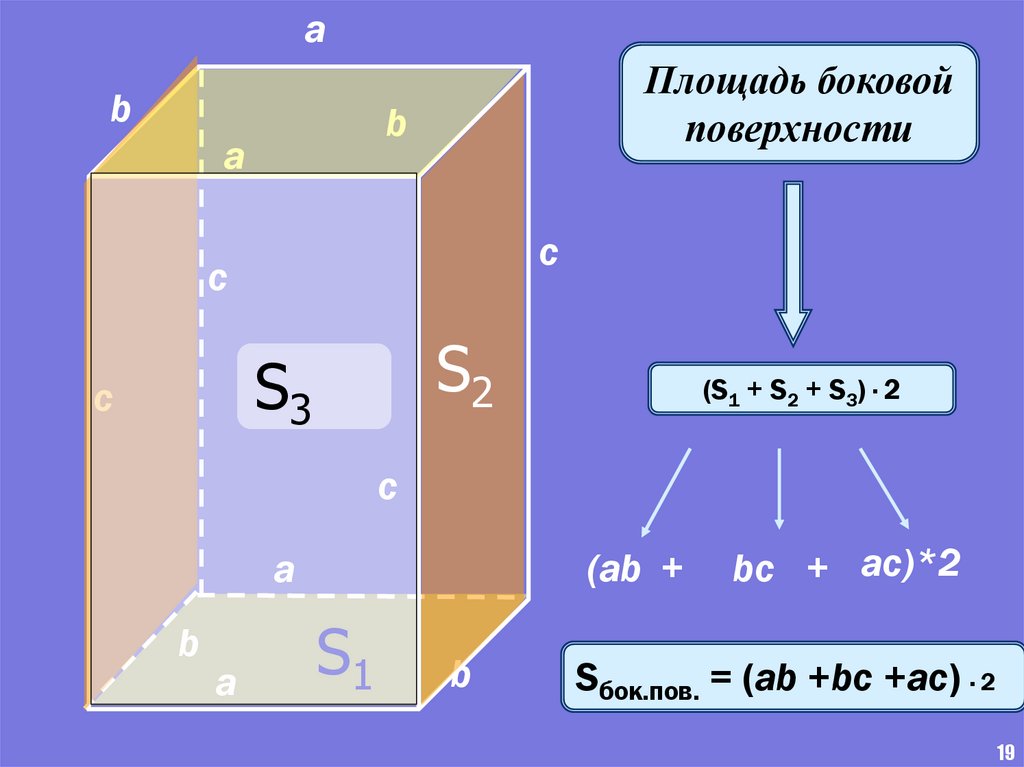
a
b
Площадь боковой
поверхности
b
a
c
c
S2
S3
c
(S1 + S2 + S3) · 2
c
(ab +
a
b
a
S1
b
bc + ac)*2
Sбок.пов. = (ab +bc +ac) · 2
19

20. ДОМАШНЕЕ ЗАДАНИЕ:

Учебник Геометрия /Погорелов/
§19
20